基于改进型PID的火炮药仓控制研究

侯大为，刘琮敏，范志国，王振明，魏继卿

(西北机电工程研究所，陕西 咸阳 712099)

基于改进型PID的火炮药仓控制研究

侯大为，刘琮敏，范志国，王振明，魏继卿

(西北机电工程研究所，陕西 咸阳 712099)

为提高某型火炮新型模块化药仓旋转选药控制的性能，基于传统PID控制算法,提出一种改进型PID控制算法。通过合理的线性化和简化处理，建立了药仓选药系统的数学模型，在此基础上，设计了基于改进型PID算法的位置环控制器，比较分析了设计的控制器和传统PID控制器在位置伺服系统的控制性能，在Maltab仿真环境下进行了建模和仿真。仿真结果表明：该算法能够提高系统型别，具有较小超调量及稳态跟踪精度。

改进型PID控制器；伺服系统；火炮药仓控制

射速是实现火炮猛烈和持续高强度打击的基础条件，全自动弹药装填系统作为地面压制火炮的重要组成部分，实现弹丸与发射药安全、快速、可靠的自动装填，提高火炮的发射速度，进而提高火炮的威力、自动化程度、快速反应能力，它是火炮武器性能高低的重要标志。

全自动弹药装填系统一般由自动化弹仓、自动化药仓、弹药协调器、输弹机和输药机组成。新型药仓是弹药自动装填系统的改进之一，实现了模块药存储和选择的功能，要求药仓运动具有可靠性好、响应速度快、稳态精度高的性能[1]。

药仓选药过程中要求每一个动作时间都很短，一般在1 s左右完成，必须具有较快的响应速度和较好的定位精度，因此对传统PID控制器进行了研究，提出了一种改进型PID控制器，以达到性能指标。在建立了药仓控制数学模型的基础上，设计了基于改进型PID控制律的药仓位置环控制器，并用Matlab仿真软件进行了仿真分析。

1 药仓运动的建模和分析

药仓安装在火炮炮塔内，采用筒式循环链形式，旋转选药驱动的方式选用主动链轮单轴驱动，因为采用单轴驱动的方式可以有效减少药仓回转运动的多边形效应影响[2]。因此，药仓旋转选药采用无刷直流电动机作为执行机构，其具有体积小、寿命长、无换相火花、运行效率高和调速效果好等特点。由于无刷直流电机与传统直流电机相似，可以利用传统直流电机的动态特性模型来表示[3]，药仓速度环的数学模型如图1所示。

图1中K1为放大倍数；ASR表示速度调节器,ACR表示电流调节器，二者均采用比例环节，分别为K2和K3；U为电机电枢电压；I为电枢电流；Ω为电机转速；R为电机电枢电阻；L为电枢电感；Km为电机转矩系数；Ke为反电势系数；J为电机轴上的等效负载转动惯量；D为粘滞阻尼系数，一般可忽略不计；TL为负载转矩，由于受电机转速、电流和逆变器驱动的限制，该药仓控制系统具有饱和非线性。其参数如表1所示。

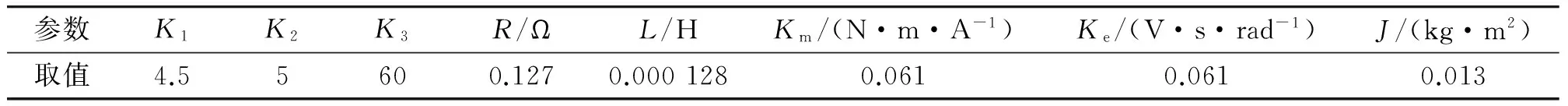
表1 药仓控制数学模型的主要技术参数

根据图1，可以得到药仓速度环的闭环传递函数为

(1)

代入数据得：

(2)

以药仓平动时最大速度和实际运行效率为依据，设定减速箱的传动比i为120，其机械传动模型如图2所示。

根据图2，得到药仓位置环所控制的传递函数为

(3)

2 药仓控制律的设计

2.1PID控制器

传统药仓运动一般采用PID控制器[4-5]，其结构如图3所示，图中Gv(s)=Kv/(1+Tvs)，Gn(s)=Kn/s，Kv为速度环放大倍数，Tv速度环时间常数，Kn为传动模型系数，Kp0、Ki0、Kd0分别为比例、积分、微分环节系数。

(4)

(5)

药仓选药的命令信号首先是加速，其次是恒速，再减速。在恒速段，可以得出系统在速度信号作用下的稳态误差为0；在加减速段，位置给定信号为R(s)=a/s3，则加减速段的稳态误差为

(6)

可以看出在加减速信号作用下存在稳态误差。

2.2 改进型PID控制器

传统PID控制器取误差作为控制量，进行比例、积分、微分组合控制，其中微分环节可以加快系统的动作，减少超调量，但是只有当误差出现变化时，微分控制才进行控制。为了在出现误差之前就实现控制，提前对输入信号进行微分处理，再与速度反馈信号进行比较，可加快系统的响应速度。因此对PID控制器的结构进行了改进设计，火炮药仓选药伺服系统的位置控制器结构图如图4所示，其中Kp、Ki、Kd分别为改进型PID控制器的比例、积分、微分环节系数。

(7)

(8)

(9)

对比式(4)和(7),改进型PID控制器和PID控制器的闭环传递函数非常类似。虽然改进型PID控制器的结构进行了改变，但是并没有改变PID控制器本质性能，都可以改善系统的闭环特征方程，通过调节比例、积分、微分系数，都可以使闭环系统的极点都位于s左半平面，因此二者具有类似的稳定性能。

对比分析改进型PID控制器和传统PID控制器的误差传递函数，由式(9)知，当Kd=1/Kv(Kn-1)，可使加减速信号作用下的稳态误差减少至0。改进型PID控制器不仅可以使恒速度信号下的稳态误差为0，而且也可以使加减速度信号下的稳态误差为0。而传统PID控制器加减速信号下的稳态误差一直存在。因此改进型PID控制器提高了系统型别，改善了位置伺服控制系统的稳定跟踪性能。

2.3 参数整定

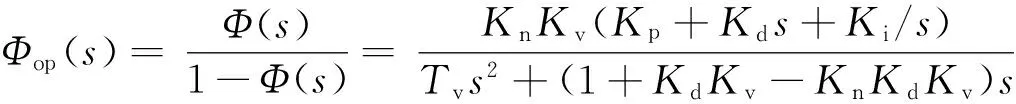
(10)

取s=jω，得到控制器的频率特性方程为

(11)

(12)

则幅频特性和相频特性分别为

(13)

(14)

根据期望的截止频率和相角裕度，可以有以下约束条件进行控制器参数的计算。

1)截止频率

为了使系统能准确地复现系统的输入信号，要求选择较大开环系统的截止频率ωc来增加带宽，但是从抑制噪声的角度来看，又不希望系统的带宽过大。因此设定合适的ωc后，有

A(ωc)=1

(15)

2)相角裕度

设定合适的相角裕度以提高系统稳定性，有

γ(ωc)=φm-π

(16)

3)低频段精度点[6]

给定药仓控制系统的技术指标，最大跟踪角速度为Ωm和最大跟踪角加速度εm，以及最大的允许跟踪误差em。将技术指标折算成等效正弦规范为φcsin(ωit)，其中等效振幅φc=Ωm2/εm，等效频率ωi=εm/Ωm。要求误差小于em的误差精度点A在ωi=εm/Ωm处的开环对数幅频特性数值为

(17)

3 仿真分析及计算

图1中，火炮药仓位置环控制器的饱和限幅为±10V，其中速度环的放大倍数为Kv=4.4，机械传动的系数为Kn=8.3，对药仓速度环传递函数进行开环频域特性分析，得到速度环的截止频率为ωv=18.7 rad/s，相角裕度为γv=28.7°。设定校正后系统的截止频率为ω0=29 rad/s，相角裕度为γ0=75°，由上节的约束条件以及式(7)等于0的约束进行计算得到Kp=0.35，Kd=0.03，Ki=0.008。为了比较控制器的性能，在上节约束条件下得到传统PID的控制器的参数Kp0=0.98，Kd0=0.023，Ki0=0.002。

在Matlab仿真软件分别求改进型PID控制系统和传统PID控制系统的等效开环系统的对数幅频特性曲线，如图5、6所示。两者的截止频率均为ω1=29 rad/s，相角裕度均为γ1=75°。

在Matlab仿真软件的Simlulik环境中，分别对两种控制器进行了仿真建模，在输入10 mrad阶跃响应信号，改进型PID控制器和传统PID控制器的阶跃响应曲线如图7所示。

时间到达1 s时，阶跃响应为10 mrad，由图7看出，改进型PID控制器的调节时间0.5 s，超调量约为 0.1 mrad，PID控制器具有响应时间0.5 s、超调量为1 mrad。因此，改进型PID控制器具有较小的超调量，更易进入稳态。

药仓选药一般不采用正弦信号，但是可以通过仿真得出控制器的跟踪性能。给定输入信号为r=10 sinθ，则跟踪输入信号的响应曲线仿真结果如图8所示。仿真结果表明，PID控制器的系统跟踪误差约为0.9 mrad，改进型PID控制器的系统跟踪误差约为0.18 mrad，跟踪精度有较大的改善，这是由于改进型PID控制器提高了系统的型别，改善了系统跟踪性能。

综合以上仿真特性曲线的分析可知，在相同约束条件下，改进型PID的控制器可以使系统设计成III型系统，构成三阶无差度系统，因此可以提高系统的稳态误差精度，并且同时保证了系统的动态性能。

4 结束语

通过合理的线性化和简化处理，建立了药仓选药系统的数学模型。针对某型大口径火炮的药仓选药控制对响应速度快和到位精度高的要求，通过对传统PID控制器研究，提出了一种改进型PID控制器。仿真结果表明，在位置环伺服系统中，通过约束条件选择合适的参数，系统设计成加速度无静差的III型系统，保证了药仓选药系统的动稳态性能，为药仓选药控制系统的工程应用提供了参考。

References)

[1]侯宝林，樵军谋，刘琮敏．火炮自动装填[M]．北京：兵器工业出版社，2010：129-131． HOU Baolin,QIAO Junmou, LIU Congmin. Automatic gun feeding[M]. Beijing: The Publishing House of Ordnance Industry, 2010: 129-131. (in Chinese)

[2]解凤娟，何宗颖，骆小平,等．基于RecurDyn的链式回转药仓多边形效应分析[J]．火炮发射和控制学报，2013(6):27-30． XIE Fengjuan,HE Zongying,LUO Xiaoping,et al.Analysis of the chain type turns round magazine polyaon effect based on RecurDyn[J].Journal of Gun Launch & Control,2013(6):27-30.(in Chinese)

[3]黄唯．无刷直流电机无位置传感器控制系统的研究和实现[D]．长沙：湖南大学，2012:10-18． HUANG Wei.The study and realization of the sensorless brushless DC motor control system[D]．Changsha：Hunan University, 2012:10-18. (in Chinese)

[4]胡松涛．自动控制原理[M]．5版．北京：科学出版社，2010：256-257. HU Songtao.Automatic control theory[M]. 5th ed. Beijing:Science Press,2010:256-257. (in Chinese)

[5]禹牛云．位置伺服系统 PID 控制策略研究与应用[D]．杭州：杭州电子科技大学，2010:11-12． YU Niuyun.Study and application of position servo system based on PID control[D].Hangzhou：Hangzhou University of Electronic Science and Technology,2010:11-12. (in Chinese)

[6]陈明俊，李长红，杨燕. 武器伺服系统工程实践[M]．北京：国防工业出版社. 2013. CHEN Mingjun,LI Changhong,YANG Yan.The weapon servo system engineering practices[M]．Beijing: National Defense Industry Press,2013. (in Chinese)

Research on Control of Artillery Charge Based on Modified PID

HOU Dawei,LIU Congmin,FAN Zhiguo,WANG Zhenming,WEI Jiqing

(Northwest Institute of Mechanical & Electrical Engineering, Xianyang 712099, Shaanxi, China)

For the purposes of improving the performance of a new type of artillery module in the control of rotation and ammunition artillery charge selection, based on algorithm of normal PID control, the improved PID control was proposed. Under reasonable hypotheses and approximations, a model of Artillery Charge system was established. As a consequence, the improved PID control law of the position loop was designed. Then, the designed control performance was compared with that of traditional PID controller in terms of tracking performance of position servo system. Modeling and simulation under Matlab environment was set up with simulation characteristic of traditional PID and improvement PID compared and analyzed. Simulation results show that using the new control algorithm improved the response rate and system bandwidth in the control of a new type of artillery module in the control of rotation and ammunition artillery charge selection, possessing a better steady state tracking accuracy.

improved PID；servo system；artillery charge control

10.19323/j.issn.1673-6524.2017.01.008

2016-03-13

侯大为(1989—)，男，硕士研究生，主要从事弹药自动装填与控制技术研究。E-mail：jiangchen.119@163.com

TJ35

A

1673-6524(2017)01-0037-05