基于局部和全局一致性的多标签分类算法
姚小慧,孙国强
(上海理工大学 光电信息与计算机工程学院,上海 200096)
基于局部和全局一致性的多标签分类算法
姚小慧,孙国强
(上海理工大学 光电信息与计算机工程学院,上海 200096)
针对局部和全局一致性的分类算法LGC未考虑标签之间的相关性,提出了一种基于局部和全局一致性的多标签分类(MLGC)算法。该方法新增加了一个标签与标签之间的约束,在分类时考虑了标签之间的相关性,再取出1/10的数据集使用该算法,求出每个标签的自适应阈值,利用阈值对整个数据集进行预测。实验结果表明,所提出算法在Emotion和Yeast数据集上均优于原来算法,将此算法应用于区域医疗大数据的项目中,也取得了良好的分类结果。
多标签分类;局部和全局一致性;标签相关性
众多学者对于分类问题提出了许多算法[1],但有许多问题无法采用单分类方法解决,例如文本领域[2-3],图片注解领域[4-6]和生物信息领域[7]。所以,多标签分类问题应运而生,引起了人们广泛的关注。解决多标签分类最简单的方法就是BR(Binary Relevance)方法[8],但它没有考虑标签之间的相关性。LP(Label Powerset)[9]方法是将问题转化为多分类问题,虽然考虑了标签之间的相关性,但是训练开销会比较大。MLkNN算法[10]用最大化后验概率来预测该样本的标签集,也没有考虑标签之间的相关性。因此本文在文献[11~13]的研究基础上,提出了一种基于局部和全局一致性的多标签分类算法MLGC(A Multi-label Classification Based on The Local And Global Consistency),不仅考虑了标签之间的相关性,而且还提出了适应于该算法的阈值,经过Matlab仿真实验,证明了该算法优于LGC(Learning With Local And Global Consistency)算法。
1 LGC正则化框架
已知数据集X=X1,X2,…,Xn,标签集Y=Y1,Y2,…,Yc,其中n为数据集总数,c为标签集总数,分类函数定义如下

(1)
其中,W是n×n的数据相关性矩阵;D是一个对角矩阵;(i,i)值等于W第i行的和;F是n×c的目标标签矩阵;Y是n×c的初始化标签矩阵,μ>0,是正则化参数。式(1)的第一项是平滑性约束,第二项是拟合约束。采用参数μ对这两个约束进行权衡。
对矩阵F求导,可得
F=β(I-αS)-1Y
(2)

2 MLGC算法
多标签学习算法只考虑了数据之间的相关性,而忽视了标签之间的相关性,当标签之间的关系密切时,那么文献[14]所提出的LGC正则化框架就会受到限制。本文提出的MLGC算法通过引入标签与标签之间的约束,避免了LGC正则化框架的限制,从而解决了多标签的分类问题。
2.1 算法原理
LGC正则化框架只考虑了两大约束,这对多标签分类来说,是远远不够的。受文献[13]的启发,在考虑多标签分类时,还应该考虑标签与标签之间的相关性,因此本文在LGC的基础上,添加了第三项约束条件,使该算法更加适用多标签分类算法。
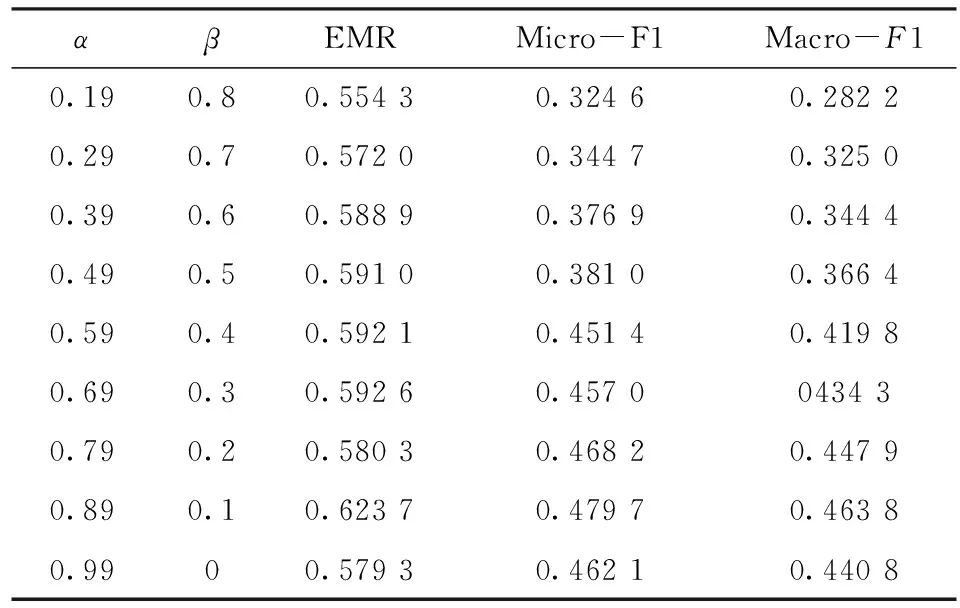
已知数据集X-{X1,X2,,,Xn}∈Rn*m,数据集X所对应的标签集共有c个标签,记为L={L1,L2,,,Lc}∈Rc*n,X中前l个数据已经分好类,其中l< F(t+1)=αSF(t)+βF(t)P+γY (3) 其中,α+β+γ=1,F(0)=Y,矩阵S和矩阵P由数据关系矩阵(4)和标签关系矩阵(5)得出 (4) (5) 对式(4)和式(5)进行归一化,得到S矩阵和P矩阵 S=D-1/2WD-1/2,P=D’-1/2W’D’-1/2 (6) 其中,矩阵D为对角矩阵,它的(i,i)是矩阵W的第i行的和,矩阵D’为对角矩阵,它的(i,i)是矩阵W’第i行的和。 至此,式(3)中的变量已逐一阐明,对其求极限,可得 (ɑS-I)F*+βF*P+γY=0 (7) 2.2 正则化框架 (8)式(8)中第一项是数据节点之间的光滑性约束,是指相邻数据节点间应该有相同的标签;第二项是标签光滑性约束,是指相邻标签节点间应该有相同的数据节点;第三项是拟合性约束,是指预测的标签值与初始值不应发生过大的变化。为了最小化Q(F),对F进行求导 (9) 化简式(9)可得 (10) 令, (11) 由式(10)和式(11)得 (αS-I)F*+βF8P+γY=0 (12) 由此,式(12)得出了与式(7)一致的结论。 2.3 自适应阈值 在文献[14]的基础上,本文根据该算法提出了适应于本算法的自适应阈值。实验中,本文选取1/10的训练集,根据MLGC算法,快速得出最后的分类矩阵F′。对于每一个标签,选取F′矩阵中属于该标签的值取其平均值,得到该标签的接受阈值Tal,选取F′矩阵中不属于该标签的值取其平均值,得到该标签的拒绝阈值Tdl,最终的阈值T1即为接受阈值和拒绝阈值的平均值 (13) 3.1 实验数据 实验采用两个不同领域的真实的数据集:Emotion数据集是有关音乐领域的数据集,在该数据集中,标签空间为6;Yeast数据集是生物领域的数据集,它是对基因片段的功能进行分类,其标签空间为14,表1描述了两个数据集的详细信息。 表1 数据集 3.2 评价指标 实验采用精确匹配率(Exact Match Ratio, EMR)[15],微平均F1值(Micro-F1)和宏平均F1值(Macro-F1)这3个性能指标,具体定义为 (14) F1 score定义如下 (15) 其中,P1是第l个标签的精确率;R1是第l个标签的召回率,所以c个标签的宏F1 score就是它们每个类别F1 score的算术平均值 (16) 微F1 score是每个实体F1 score的算术平均值[15],具体定义为 (17) 3.3 实验结果及分析 为验证本文算法的有效性,与已有的LGC算法进行比较,在LGC算法中,本文取 。对于本文算法,采用十折交叉验证法来选择参数,即把训练集分成10份,取其中9份作为训练集,剩下的一份作为测试集,实验结果如表2和表3所示。 表2 十折交叉法在Emotion数据集上的性能 表3 十折交叉法在yeast数据集上的性能 实验结果表明,α=0.89,β=0.1时,算法得到最优解。这表明,在取值过程中,α与β并不是越大越好,他们二者相互制约,当α较大时,说明预测的节点更有可能与其相似的数据节点具有相同标签,当β较大时,说明预测的节点更有可能具有与其标签相似的标签。 表4 K折交叉法在Emotion数据集上的性能(α=0.89,β=0.1) 表5 K折交叉法在Yeast数据集上的性能(α=0.89,β=0.1) 采用K折交叉验证法(K=2~10),在Emotion和Yeast数据集上采用最佳参数值,即α=0.89,β=0.1进行试验,试验结果如表5和表6所示,在这两个数据集上,随着K值的增大,即训练集变大,精确匹配率、微平均和宏平均这3个指标均有上升的趋势。当K值一定时,MLGC算法在这3个性能指标上的值均大于LGC算法在这3个指标上的值,这表明MLGC算法整体上均优于LGC算法。 标签之间的相关性是多标签分类中不可忽视的一项重要因素。本文提出了考虑标签相关性的MLGC算法,提供了其迭代算法和框架。实验结果表明,MLGC算法均优于LGC算法,可以提高多标签的分类效果。 [1] Tsoumakas G,Katakis I.Multi label classification:an overview[J].IEEE Intelligent Systems,2010,25(4):19-25. [2] Lewis D,Yang Y, Rose T,et al.RCV1:A new benchmark collection for text categorization research [J].The Journal of Machine Learning Research,2004,5(2):361-397. [3] Moffat A,Zobel J.Self-indexing inverted files for fast text retrieval[J].Acm Transactions on Information Systems,2015,14(4):349-379. [4] Boutell M R,Luo J,Shen X,et al.Learning multi-label scene classification[J].Pattern Recognition,2004,37(9):1757-1771. [5] Peng Y,Ngo C W.Clip-based similarity measure for query-dependent clip retrieval and video summarization[J]. IEEE Transactions on Circuits & Systems for Video Technology,2006,16(5):612-627. [6] Greenspan H, Goldberger J, Mayer A. Probabilistic space-time video modeling via piecewise GMM[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2010, 26(3):384-96. [7] Jiang J Q,Mcquay L J.Predicting protein function by multi-label correlated semi-supervised learning[J].IEEE/ACM Transactions on Computational Biology & Bioinformatics,2012,9(4):1059-69. [8] Boutell M R,Luo J,Shen X,et al.Learning multi-label scene classification[J].Pattern Recognition,2004,37(9):1757-1771. [9] Tsoumakas G,Katakis I,Vlahavas I.Random k-labelsets for multilabel classification[J].IEEE Transactions on Knowledge & Data Engineering,2011,23(7):1079-1089. [10] Zhang M L,Zhou Z H.ML-KNN:A lazy learning approach to multi-label learning[J].Pattern Recognition,2007,40(7):2038-2048. [11] Zhang M L.An improved multi-label lazy learning approach[J].Journal of Computer Research and Development,2012,49(11):2271-2282. [12] Zhou D,Bousquet O,Lal T N,et al. Learning with local and global consistency[J].Advances in Neural Information Processing Systems,2004,16(4):321-328. [13] Xu J J,Jagadeesh V.Multi-label learning with fused multimodal birelational gaph[J].IEEE Transactions on Multimedia,2014,16(2):403-412. [14] 郑伟,王朝坤,刘璋,等.一种基于随机游走模型的多标签分类算法[J].计算机学报,2010,33(8):1418-1426. [15] 史仍浩,陈秀真,李生红.基于流形学习的社会化媒体网络数据分类[J].计算机应用研究,2013,30(3):692-694. The Multi-label Classification Based on the Local and Global Consistency YAO Xiaohui,SUN Guoqiang (School of Optical-Electrical and Computer Engineering,University of Shanghai for Science and Technology,Shanghai 2000235,China) The multi-label classification didn’t take the relationship of the labels into consideration,so this paper improved LGC and proposed a multi-label classification based on the local and global consistency(MLGC). The method added a new constraint between labels, which consider the correlation between tags. Besides, this paper put forward a suitable threshold. Experimental results based on the emotion and yeast data sets shows this method is superior to LGC.Then the algorithm is applied to the project of medical,which also achieved great result. multi-label classification;local and global consistency;label relation 2016- 06- 20 国家高技术研究发展计划(863计划)基金资助项目(2015AA020105) 姚小慧(1992-),女,硕士研究生。研究方向:机器学习。孙国强(1962-),男,副教授。研究方向:嵌入式应用系统开发。 10.16180/j.cnki.issn1007-7820.2017.03.002 TP301.6 A 1007-7820(2017)03-004-04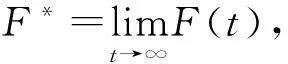
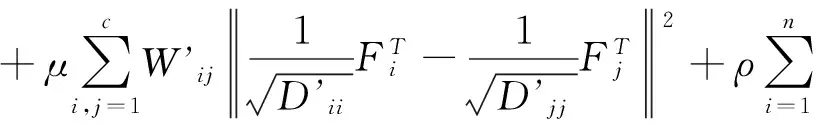
3 验证






4 结束语

