概念活用思路宽广

文︳申娜

概念活用思路宽广

文︳申娜

李邦河院士在《数的概念的发展》报告中指出：“数学根本上是玩概念的，不是玩技巧，技巧不足道也。”细细体会这话，运用到数学学习中，还真是那么回事。

例如，推导一元二次方程ax2+bx+c=0（a≠0，b2-4ac≥0）根与系数的关系时，我们通常是求出方程的两个根，再算两根之和与之积。如果用方程根的概念，则另有一番风光。

设x1，x2是方程ax2+bx+c=0（a≠0，b2-4ac≥0）的两根，则

ax12+bx1+c=0，ax22+bx2+c=0。

两方程相减并分解因式，得（x1-x2）[a（x1+x2）+b] =0。

若x1=x2，则b2-4ac=0，b2=4ac，方程有两个相等的实根

若x1≠x2，则a（x1+x2）+b=0，

将两方程相加并配方，得[a（x1+x2）2-2x1x2]+ b（x1+x2）+c=0，将代入并化简，得x1x2=

虽然上述过程并不比用求根公式计算简便，但也打开了思维的另一扇窗，使我们思考问题的路子更宽广。

许多数学概念中就有数学表达式，如椭圆、双曲线的定义，本身就是用数学式子叙述的。在思考问题时，很多题目就可灵活运用定义求解。

如，设点F1，F2分别为椭圆的左、右焦点，P为椭圆上任一点，又有一定点M（6，4），求|PM|+|PF1|的最大值。

很容易想到设点P（x1，y1），或者设P（5cosθ， 4sinθ）代入椭圆方程，得到一个等式，然后又代入|PM|+|PF1|中，求函数的最大值。这样做思路易得，求解却难。如果利用椭圆定义的表达式，则会显得简便。

易求得F1（-3，0），F2（3，0），依据椭圆定义，有|PF1|+|PF2|=10，则|PF1|=10-|PF2|。

于是，|PM|+|PF1|=10+|PM|-|PF2|≤10+|MF2|=

当|PM|-|PF2|=|MF2|时，取得最大值15。那么，取得最大值时，点P的坐标是什么？从图形上发现，当点P是线段MF2的延长线与椭圆的交点时，才能满足|PM|-|PF2|=|MF2|。直线MF2的方程是与椭圆方程联立，解得P（0，-4）或显然，点P（0，-4）满足条件。

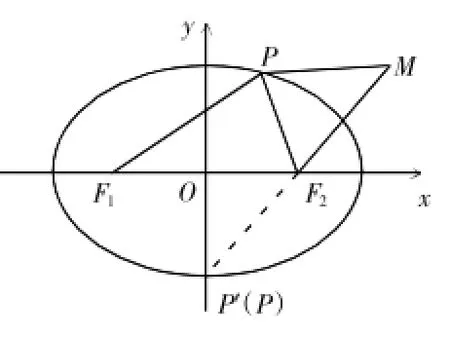
椭圆、双曲线定义中，动点到两定点的距离和或差是定值。那么，动点到两定点的距离商如果是定值，动点的轨迹是什么呢？

设动点是P（x，y），两定点分别是F1（-a，0），F2（a，0），a＞0，且，λ＞0，且λ≠1。那么，，化简，得

（1-λ2）x2+（2a+2aλ2）x+（1-λ2）y2+（a2-a2λ2）=0。

由于λ≠1，则1-λ2≠0，那么上式表示的是圆的方程，动点P（x，y）的轨迹是圆。这个圆叫阿波尼斯圆。运用阿波尼斯圆可以简解下面两道高考数学题。1.（2008年江苏）满足条件的△ABC面积的最大值是_________。

2.（2014年湖北）已知圆x2+y2=1和点A（-2，0），若定点B（b，0）（b≠-2）和常数λ满足：对圆O上任意一点M，都有|MB|=λ|MA|，则b=_______，λ=________。

第1题中，设A（-1，0），B（1，0），C（x，y），则λ=。由上面的阿波尼斯圆的方程，得点C的轨迹是：（x-3）2+y2=8（除去点（，0））。由于|AB|=2是定值，要使△ABC的面积最大，只要点C到AB的距离最大即可。显然，最大距离是圆的半径，因此，最大面积是

第2题中，设M（x0，y0），由|MB|=λ|MA|，得

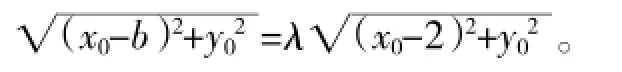
（作者单位：邵东县第一中学）