概率论与数理统计之基本概念本质内涵教学探讨

李军+曹旭+刘鹏+朱守平

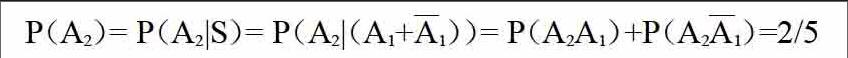
摘 要 统计推理在目前的科学研究中起着中心位置，概率论与数理统计作为其入门的基础课程，正确掌握其基本概念的本质内涵对以后学生从事科研工作显得尤其重要。本文拟根据目前概率论与数理统计的教学大纲内容探讨一些学生在学习时容易忽视其本质的概念，并结合实际的例子深入了解其概念的内涵。

关键词 独立性 条件概率 相关系数 数字特征 最大似然估计

中图分类号：G424 文献标识码：A DOI：10.16400/j.cnki.kjdkx.2017.02.046

Abstract Statistical inference plays a central location in the current scientific research. The course of probability theory and mathematical statistics is a introductory course of statistical inference， it is especially important to correctly grasp the nature of basic concepts of probability theory and mathematical statistics for those students who will engage in research works in the future. Based on the current syllabus of probability theory and mathematical statistics， this paper explores some of concepts which are easy to overlook their nature by students while they are studying， combined with practical examples to further understand the nature of the concepts.

Keywords Independence； conditional probability； correlation coefficient； digital features； maximum likelihood estimation

2002年美国国家基金委组织了有关“当前和显露出来的概率论学科中研究机遇”的系列报告，指出概率论与数理统计在当前已是一门核心数学学科，其概率推理理论在目前不同学科中解决其研究问题有着显著功效，其理论研究的重要性也呈现爆炸性的增长。[1]然而，鉴于目前相当一部分科研论文中使用的统计方法存在概念性的错误，[2]国际著名的学术期刊《科学》在2014年表示将增加一个特别的统计学专家团队来检验投稿论文中的统计方法是否有误。[3]其他重要的学术刊物，包括《自然》也相继提出了一些检查方案来保证论文中统计方法的使用得当。[4]统计推理应用的广泛性同基本概念错误理解之间的尖锐矛盾提示研究者在学习统计推理理论时不能停留在概念的表象，需要深入理解其本质内涵。2015年研究生入学考试的数学（一）科目中统计推理部分的试题就能很好的考察学生是否真正掌握了统计推理基本概念的本质。2015年研究生入学考试的数一试卷中概率论与数理统计部分内容一共是34分，内容覆盖了随机事件性质，概率分布，数值特征计算，假设检验等内容。从题目的难易程度来讲，在掌握基本概念内涵的前提下，基本上不存特别难的题目。但在笔者小范围的调查表明，越是考察基本概念的题越是失分严重，反而有固化解题步骤的题目得分就较多。针对目前统计推理的重要性和基本概念理解不够透彻的普遍问题，再一次为我们从事概率论与数理统计的教学工作者提出了一个在教学中一直强调的问题，如何让学生在学习过程中抓住基本概念的内在实质。结合概率论与数理统计的教学大纲，以及近几年的教学过程中学生的反馈和自己的思考，针对大学本科工科概率论与数理统计部分教学中的一些基本概念内涵教学做一个初步探讨。

1 随机事件之间相互独立的本质是随机事件概率的独立性

随机事件之间存在多种关系，其中互斥（互不相容）和相互独立在概率论的学习中使用最多，学生也最容易混淆。当内容延伸到随机变量时，随机变量的相互独立和随机变量间的相关性又会带来混淆。在讲授这些定义时，若强调其本质并加以对比就能使学生比较容易区分随机事件之间的不同关系描述的差异。首先是定义的范围不同，互斥关系定义在样本空间中，反映事件的集合性质；而相互独立和相关性是定义在事件概率的数值关系中，反映事件间的概率属性。其次相互独立表述是事件概率的一般数值关系，而相关性表述的是事件的线性关系。通过强调随机事件相互独立的本质是随机事件概率的独立性，就能辨别随机事件互斥同随机事件独立之间的关系：两事件互斥推导不出它们相互独立，同时两事件相互独立也推导不出它们互斥。通过强调随机事件相互独立反映随机事件概率间的一般数值关系，就能辨别随机事件相互独立同相关性之间的区别：随机变量相互独立可以推導出它们之间不相关，但是反之不行。[5]

2 条件概率同普通概率定义本质的统一性

条件概率定义为：设A，B为两个事件，且P（A）>0，则有事件A发生的条件下事件B发生的概率为P（B|A）=P（AB）|P（A）。该定义明确直观，易于使用，在实际使用时一般都是基于单个事件概率已知前提下求条件概率，但是通过挖掘其本质，并同普通事件的概率建立关联，那么在使用的时候不会再将条件概率同一般事件概率割裂，而会形成一个统一概念。对于任意随机事件C，记其概率为P（C），当同条件概率的定义建立联系时，我们引入样本空间S，则有P（C）=P（C|S）=P（CS）/P（S）=P（CS）。通过这种变化形式可有效的解决特定事件概率不易求解的问题；同样，这也是全概公式的实质所在。

实例1：设2人抓阄，一共5个阄，其中2个阄中写有“是”字，三个空白。问抓阄是否同次序有关。

解析：分析可知所求为依次抓阄时抓到“是”的概率是否相同。

设A1，A2分别为第1，2个人抓到“是”字的事件。则有

P（A1）=2/5

故抓阄同次序无关。该方法可以延伸到更多人数抓阄的问题。

3 二维正态随机变量同一维正态随机变量之间的纽带关系——相关系数

正态随机变量有许多优良的统计性质，也是概率论与数理统计课程中重点的分布。学生一般对于一维的正态分布有较深刻的认识，但是一旦扩展到了二维及二维以上的正态分布时就不容易掌握。而二维正态分布同一维正态分布之间有很强的相关性；比如（X，Y） 符合二维正态分布，则其关X于和关于Y的边缘分布就是一维正态分布。二维正态分布的求解在一些特定场合可以转化为一维正态分布的求解，其纽带关系就是相关系数。二维正态分布中，X，Y相互独立的充分必要条件是X，Y相关系数为零。当二维正态随机变量中相关系数为零，则二维正态随机便分解成两个独立的一维正态分布随机变量的乘积。

实例2：设二维随机变量（X，Y）服从正态分N（1，0；1，1，0）布，则P（XYY<0）= （2015年研究入学考试题14）。

解析：因为（X，Y）～N（1，0；1，1，0），其中X，Y，相关系数为0

故有X～N（1，1），Y～N（0，1），且X，Y相互独立

进而有X1～N（0，1），且与Y相互独立

故由标准正态分布的性质可得到结果

P（XYY<0）=P（（X1）Y<0=P（X1<0，Y>0）+P（X1>0，Y<0）=1/2

4 随机变量的数字特征是常量

随机变量的分布一旦确定，其数值特征是常量；在实际的使用中，一般不会明确随机变量的分布形式，只是指称随机变量符合某种分布，在这个前提下，随机变量的数值特征一般用一个符号表示。如果不知晓随机变量的数值特征是一个常量，在解题的过程就会发生把数值特征当作变量使用。在教学的过程中一定要多次强调此概念。尤其在讲授方差计算公式的时候，可以通过对其的证明来强调随机变量的数值特征是常量这一概念。[5]

在此强调E（X）是一常量，并且也附加强调D（X）也是一常量，类似于数字特征性质中常数符号a，进而就可以利用已学习过的数学期望的性质得证。

5 最大似然估计方法其本质是使得似然函数取最大值时未知参数的取值就为该未知参数的最大似然估计值

在常规最大似然估计方法的教学中，一般会总结该方法为一个标准的流程，学生在学习的时候也会以记忆该流程作为最终的目的，当解题的条件稍微偏离常规的流程，學生就不知所措，不知道该如何处理；如果我们在教学的过程中首先让学生明确最大似然原理的本质意义，就会依据最大似然原理来对常规流程做一变通。2015年考研的最后一个题就很好的体现这种思维。

实例4：设总体X的概率密度为：

其中 为未知参数，X1，X2，……，Xn为，来自该总体的简单随机样本。求 的最大似然估计量（2015年研究入学考试题23.II）。

解析：该题目的求解目的非常清楚，按照解题流程按步推进。

到了这一步发现对似然函数对数求导并不能使之为0，有些同学就卡到了这儿。如果学生知道这步对似然函数对数求导的目的是什么，就可轻易获得 的估计量。第二步的目的通过求解似然函数获得最大值时未知参数 的取值，也就是该未知参数 的估计量。既然不能为零，那么我们就探讨下这个求导后所得函数的特点，发现该导数函数是关于 单调增加；而由题目中的定义知 的取值范围为： ≤x≤1，那么我们就能获取 的估计量为：=min{x1，x2，…，xn}。

总之，在大学本科工科概率论与数理统计的教学中，把握住概念本质内涵教学方法，并同学生讨论清楚，就能辨别一些容易混淆而难以理解的概念，并且使得学生在理解概念的本质后举一反三，相关的概念和内容就能轻松掌握，同时也能调动学生的学习积极性和主动性，也能为以后学生从事相关科研工作做打好统计推理的坚实基础，培养他们自主学习的能力。

本文受西安电子科技大学教学提升计划教学改革项目（TSLS1506）及新实验开发与新实验设备研制及实验教学改革项目（SY1565）资助

参考文献

[1] 林正炎，苏中根，张立新.当前概率学科中的研究机遇.数学进展，2004.33（2）：129-140.

[2] Nuzzo， R.，Scientific method： statistical errors. Nature， 2014. 506（7487）： p. 150-2.

[3] McNutt， M.，Raising the bar. Science， 2014. 345（6192）： p. 9.

[4] Collins， F.S.and L.A.Tabak， Policy： NIH plans to enhance reproducibility. Nature， 2014. 505（7485）：612-3.

[5] 盛骤，谢式千，潘承毅.概率论与数理统计.高等教育出版社，2008.