改善多径效应对二次雷达测角精度影响研究
刘小兵,魏永辉,朱 方,甘宸伊
(中国人民解放军63788部队,陕西 渭南 714000)
改善多径效应对二次雷达测角精度影响研究
刘小兵,魏永辉,朱 方,甘宸伊
(中国人民解放军63788部队,陕西 渭南 714000)
多径效应是影响和限制单脉冲二次雷达探测性能的最主要因素。为了削弱多径效应对二次雷达测角精度的影响,提出了OBA曲面函数结合累加权重的处理方法。通过理论分析及对实际接收信号进行处理,结果表明该方法能有效地降低干扰并且明显提高测角精度。
二次雷达;多径;OBA曲面函数;累加权重
0 引 言
随着现代航空运输业的飞速发展,飞行密度日益增加,航管二次雷达在空中交通管制中越来越发挥着不可替代的作用[1]。随着二次雷达系统应用的不断深入,实际监视需求对目标的探测能力要求也越来越高。在二次雷达的各项技术性能指标中,测角精度是一个较为关键的性能指标。它不仅影响二次雷达自身的使用,而且直接关系到和一次雷达进行数据关联的准确性,进而影响一、二次雷达的数据融合及整个系统的性能[2]。
二次雷达测角技术发展相对成熟,从常规的滑窗测角技术到幅度单脉冲测角技术,虽然能够达到较精确的测向水平,但是在恶劣的电磁环境下,尤其是在受到多径干扰影响时,随着信号的衰减,测向精度就会明显降低,雷达设计人员通常只能被动地采用地面天线的合理选址来减轻多径导致的问题[3]。因此,本文提出了OBA曲面函数结合累加权重处理的方法,可以有效地提高雷达测角精度,削弱多径效应的影响。
1 二次雷达测角原理
现代的二次雷达采用单脉冲体制,其测角方法通常是幅度单脉冲法。该测角方法是根据天线特性获取一组应答信号的和/差幅度值及符号信息,根据和/差幅度的比值及符号信息确定目标在当前波束中心指向的偏移值,从而获取目标准确方位。目标方位的计算公式如下:
TA=BA+OBA
其中,TA为目标相对于参考0°的真实方位角度,BA为二次雷达天线中心轴相对于参考0°的方位角度,OBA为目标相对于二次雷达天线中心轴的偏移角度。
天线中心轴方位(BA)可以根据天线转台的方位码盘获取。码盘最小分辨力可以达到360/(214)°(该二次雷达采用214位对360°方位进行量化),甚至更高。因此,目标方位(TA)的准确性主要是取决于目标相对天线中心轴向的偏移角度(OBA)[4-5]。幅度单脉冲测角原理框图如图1所示。
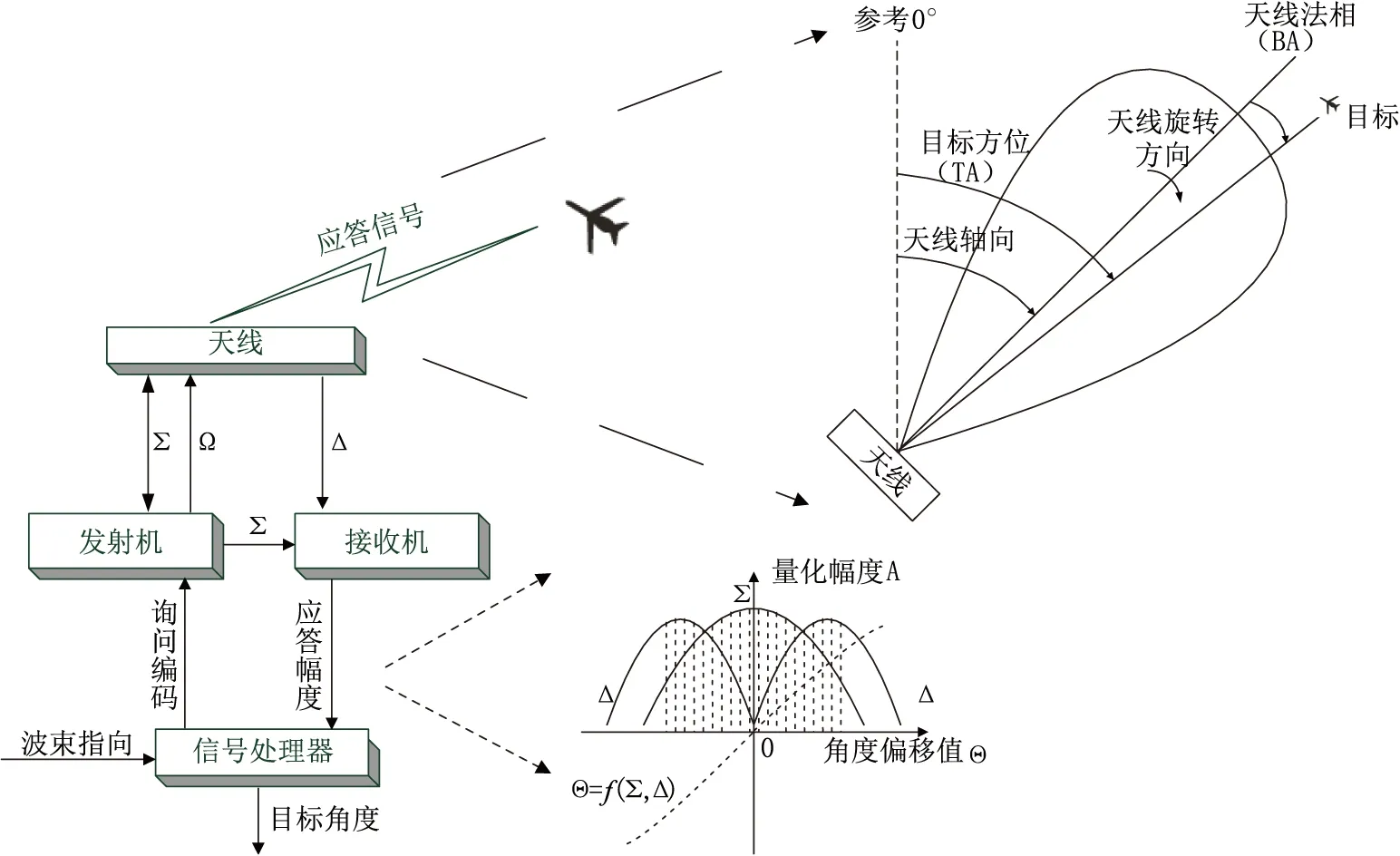
图1 幅度单脉冲测角基本原理图
目标应答信号相对天线轴向的入射角度不同,根据天线方向特性能够获取一组和幅度(∑)/差幅度(△)比值与偏移方位(OBA),进一步得到曲线OBA=f(∑,△)。因为天线的方向特性与接收机的线性量度是固定的,所以曲线OBA=f(∑,△)是可以预先得到的。然而,由于外部多径效应的干扰,加上雷达内部的噪声和校准误差,使得天线固定参数所给出的OBA表并不能完全反映实际情况,致使二次雷达的测角产生误差。
2 多径效应对目标测角精度的影响
影响和限制二次雷达探测性能的最主要因素是多径效应。多径即应答发射机和地面站接收机之间存在不只一条信号路径。在这些路径中,只有一条是发射机和接收机的直接路径,此外还存在其他路径,如地物和建筑物之类反射形成的多个信号路径[6]。由于二次雷达使用短脉冲串,直射信号和反射信号在时间上形成交错或完全分开,其时间差会改变应答脉冲特性数据,从而导致解码错误或产生一个或多个虚假目标,并通常伴随信号的衰减[7]。
直接路径和反射路径间的关系有多种情况,从直射方向和反射方向的方位间隔来区分,大致可分类为3种[3]:
(1) 地面反射信号和直接路径信号同一垂直面达到;
(2) 物体或者倾斜地面反射信号与直射信号有一个小的水平夹角,但是信号可在相同的波束滞留时间内被探测到;
(3) 物体或者倾斜地面反射的信号与直射信号有一个大的水平夹角。
所有这3类多径又可以分为两小类:
•反射信号与直射信号两个路径的信号在时间上存在很小的差异,这样通过两个路径到达的相同脉冲就会出现重叠;
•反射信号与直射信号两个路径的信号在时间上存在很大的差异,这样通过两个路径到达的相同脉冲就有部分重叠或不重叠。
不同的反射现象会产生不同的效果,如表1所示。
结合实际环境,目标应答信号在传播途中遇到复杂地形地貌,尤其是不规整的山脉,极易形成直射与反射信号零角度和小水平角度短路径叠加,产生的能量衰减或和、差特性扰乱,进而使得接收信号幅度产生异变,直接导致OBA的取值函数f(∑,△)的输入自变量的差异,从而OBA值获取不准确,造成目标的方位角(TA)不准确,如图2所示。

表1 多径类型及造成的系统误差
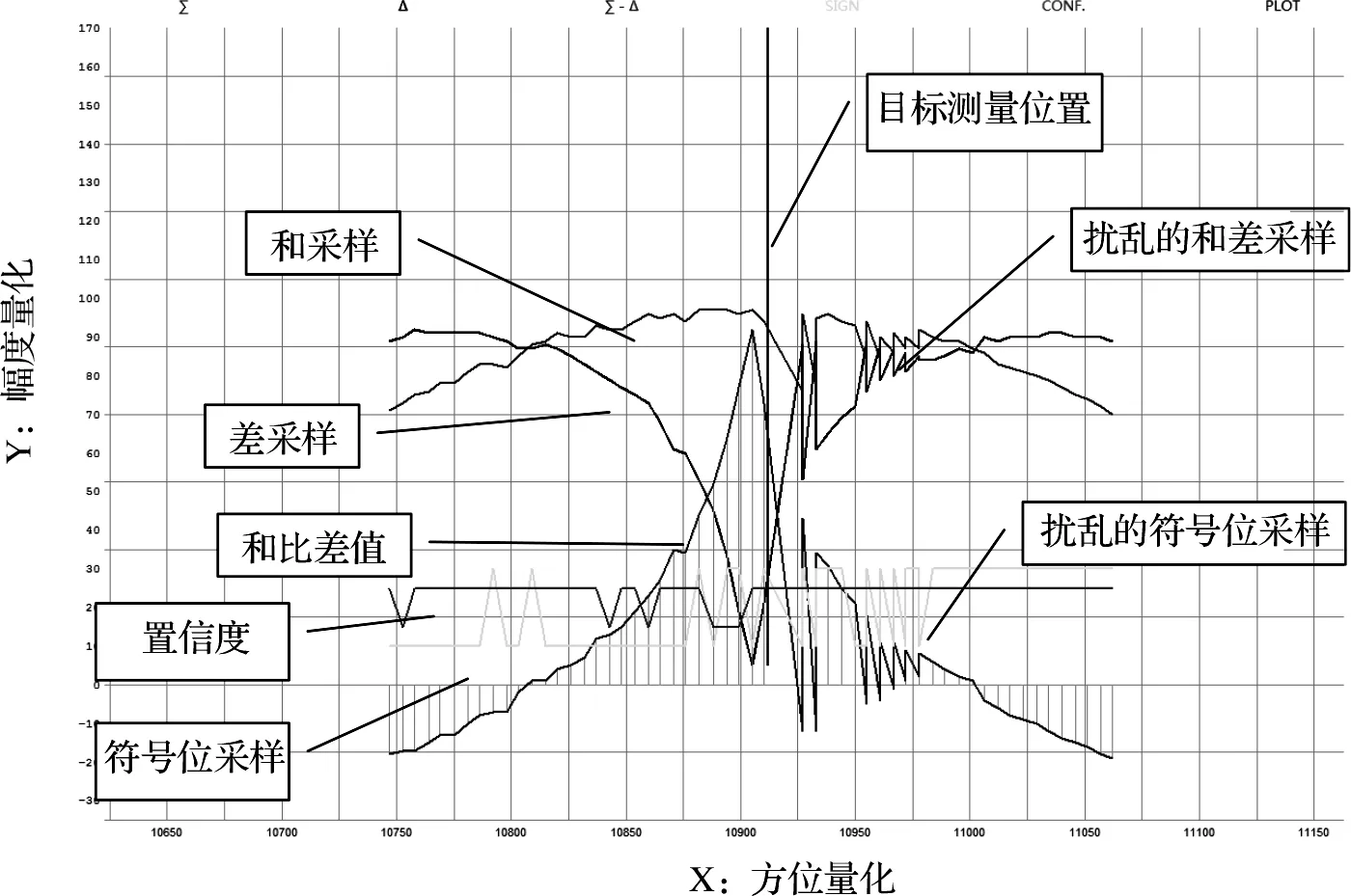
图2 异常目标应答幅度图形
对付多径效应的影响是有一定难度的。这应综合考虑以下方面:在询问阶段地面天线波束失真带来的系统问题、在应答阶段地面天线波束失真问题、在应答处理中脉冲检波和滤波问题等。本文主要从应答信号处理方面入手,提出了改善二次雷达测角精度的方法措施。
3 改善单脉冲测角精度的方法措施
3.1 OBA曲面函数方法
传统的平面式OBA取值方法是采用线性函数作为获取OBA值的函数,利用matlab对二次雷达实测的目标原始应答信息进行高斯拟合,获取传统的平面式OBA取值函数关系式。
由于每个目标都由多次原始应答的凝聚形成,因此收集目标原始应答信息。应答信息中必须的要素如表2所示。
将某个目标的原始应答按照“目标和通道幅度”、“目标差通道幅度”、“目标方位”提取出来,形成“(∑-△)-方位”偏移图,如图3所示。使用MATLAB自带的“cftool”工具,把收集到的典型原始应答数据中的“目标和通道幅度”、“目标差通道幅度”、“目标方位”进行拟合,则拟合出高斯曲线公式,并且获取常数a1、b1、c1、a2、b2、c2,因此得到函数f(∑-△)。

表2 必须收集的原始应答信息要素
其中x为∑-△。高斯拟合出的参数如表3所示。
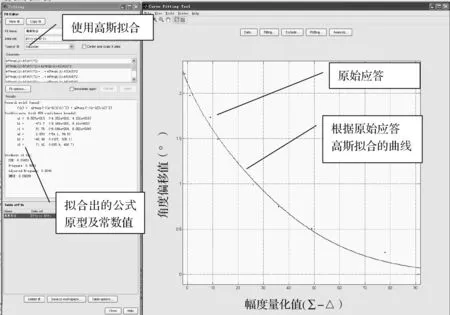
图3 高斯拟合出OBA偏移(使用matlab的cftool工具)
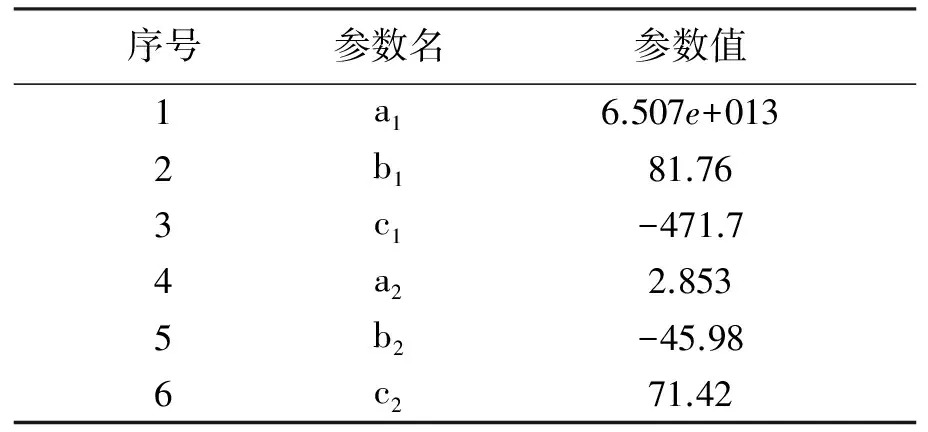
序号参数名参数值1a16.507e+0132b181.763c1-471.74a22.8535b2-45.986c271.42
在信号源与天线之间的距离固定且信号的强度一定的情况下,和、差的比值是固定的。但是,实际情况中,飞行目标的距离是在不断变化的,从天线、接收机获取到的目标幅度比值(△/∑)是随着目标的距离(R)的增大是递减的,并且不是线性关系。利用matlab对二次雷达实测的目标原始应答信息进行高斯拟合,获取f(R)函数关系式。
将所有收集到的原始应答数据中的“距离”与“目标和通道幅度”提取出来,形成“距离”-“目标和通道幅度方位”图形,如图4所示。使用MATLAB自带的“cftool”工具,把所有收集到的原始应答数据中的“距离”与“目标和通道幅度”进行拟合,拟合出高斯曲线公式,并且获取常数aa1、bb1、cc1、aa2、bb2、cc2,因此得到函数f(R)。
其中x为R。高斯拟合出的参数如表4所示。
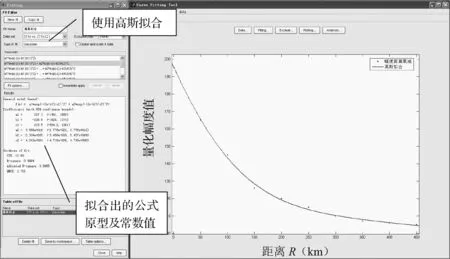
图4 高斯拟合出距离衰减曲线(使用matlab的cftool工具)

序号参数名参数值1aa1197.32bb1-226.83cc1233.54aa23.558e+0165bb2-2.334e+0056cc24.043e+004
OBA曲面函数方法是采用曲面函数作为获取OBA值的函数,因此引入距离(R)因素,获取OBA值与目标距离、和幅度、差幅度的关系函数OBA=f(△,∑,R),从而获取单次信号在自由空间中的准确OBA值。考虑距离R的因素之后,OBA的取值函数应优化为
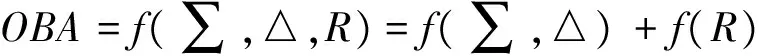
3.2 累加权重处理
通常情况下,在同一组脉冲数据中,和、差幅度比值最大的数据,在方位上最靠近二次雷达询问天线的法向,也最接近目标的真实方位。因此,在处理每一组有效数据时,增加和、差幅度比值最大时的方位的权重,使最终计算的数据更接近于目标真实方位。
其中,TA为目标方位,Ai为单次方位采样值,Ac为中心位置方位,m为增加的中心位置采样权重数,n为全部有效采样次数。在不使用中心权重方法时,m值取1,表示中心位置方位只参与一次计算。使用中心权重方法时,m的取值应大于1。根据实际情况,m值的选取需要考虑到数据处理能力,保证监测的实时性,所以权值应折中合理选取。
3.3 结果验证
本文采用以上改进方法对二次监视雷达实装数据进行验证。首先调出预处理的信号数据,如图5所示,信号和幅度、差幅度,以及和、差比幅值曲线明显比图2规整,目标测量位置基本处于和、差比幅曲线的尖峰处。其次,选取适当航线的航迹数据,以GPS数据作为真值,分析其测角标准误差(均方根误差)。图6(a)为常规单脉冲测角方法所得出的一次差曲线,图6(b)为累加权重的OBA曲面函数测角法所得出的一次差曲线,对比发现优化后的测角方法使得误差曲线变得平滑,减少了多径效应的影响。
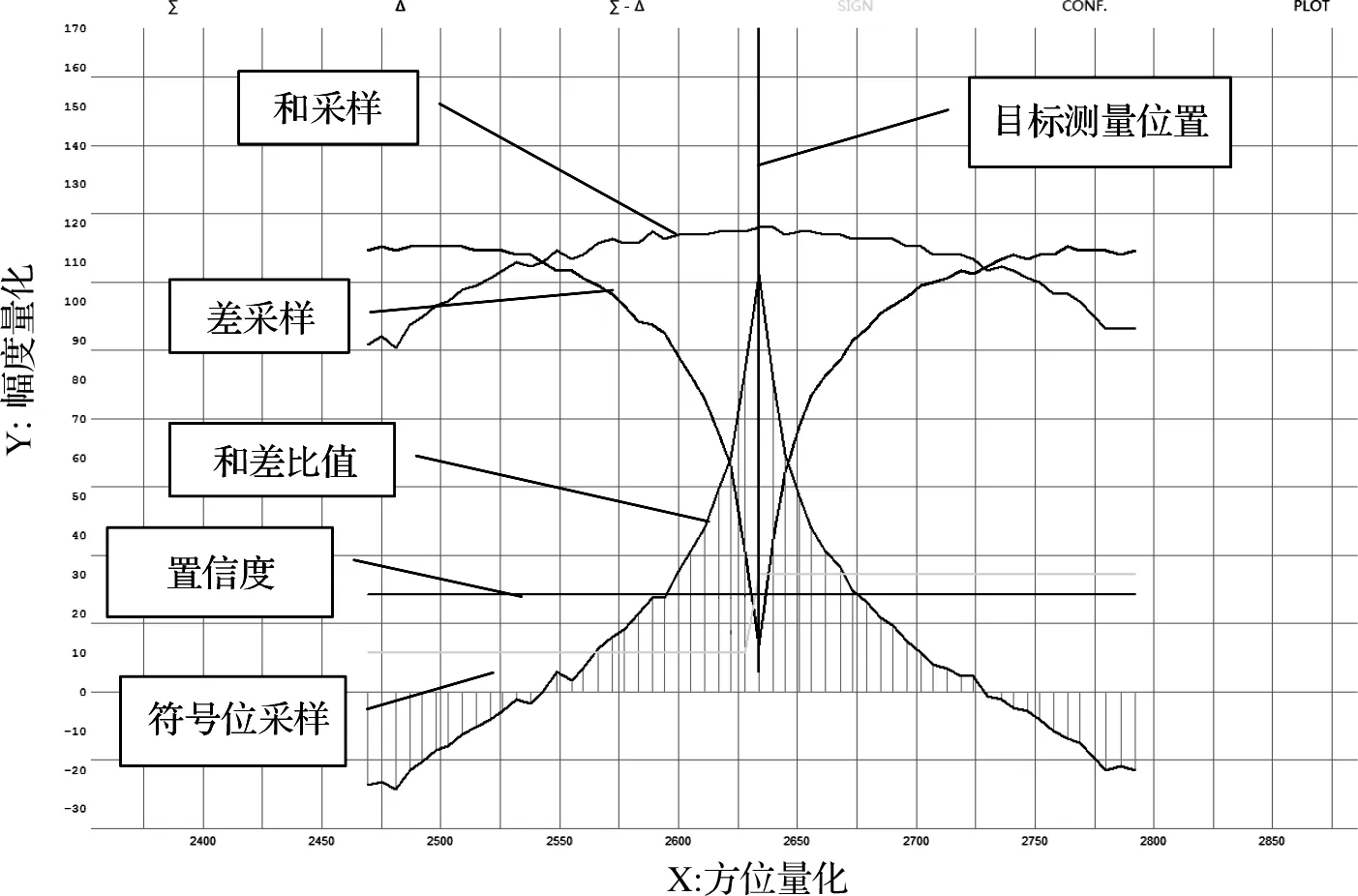
图5 正常目标应答幅度图形
4 结束语
针对多径效应产生干扰、影响到二次雷达的测角精度的普遍现象,本文提出了OBA曲面函数方法,取代了传统的平面式OBA取值方法,同时采用累加权重的处理方法,增加和、差幅度比值最大时方位的权重,提高测角的准确度。通过对实际数据的分析处理显示,本文所述OBA曲面函数结合累加权重方法的使用显著地提升了二次雷达系统在复杂环境条件下的测角精度。
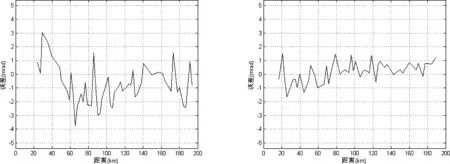
(a)常规单脉冲测角法 (b)累加权重的OBA曲面函数测角法
[1] Surveillance radar and collision avoidance systems[Z]. MAnnex10 to the convention on international civil aviation,ICAO, 1998.
[2] 吕江涛,袁鸯,韩改弟. 航管二次雷达测量精度分析及改善方法 [J]. 现代雷达, 2010(3):11-12.
[3] 张尉,徐炎祥.二次雷达原理[M].北京:国防工业出版社,2009(5):63 -64.
[4] JACOVITTIG. Performance analysis of monopulse receivers for secondary surveillance radar[C]. IEEE, 1983.
[5] Chun ping Gu. DLD-100 type monopulse secondary surveillance radar for air traffic control[C].Radar,Proceedings CIE International Conference,1996.
[6] 钟琼,吴援明,黄成芳.二次雷达系统干扰等问题的解决方法[J].电视技术,2005(2):138-142.
[7] 张虹.单脉冲二次雷达的研制和改进[J].现代雷达,2001(6):24 -27.
Research on improving multipath effect on angle measurementaccuracy of secondary surveillance radar
LIU Xiao-bing, WEI Yong-hui, ZHU Fang, GAN Chen-yi
(Unit 63788 of the PLA, Weinan 714000, China)
The multipath effect is the most important factor that can affect and limit the detection performance of the monopulse secondary surveillance radar. In order to reduce the influence of the multipath effect on the angle measurement accuracy of the secondary surveillance radar, the OBA surface function is proposed combined with the accumulative weight method. Through the theoretical analysis and the processing of the signals received, the results indicate that the method can effectively reduce the interference and improve the angle measurement accuracy.
secondary surveillance radar; multipath; OBA surface function; accumulative weight
2017-01-05;
2017-01-21
刘小兵(1985-),男,工程师,硕士,研究方向:雷达及雷达对抗、航天测控;魏永辉(1972-),男,高级工程师,工程硕士,研究方向:测控设备及测控数据处理;朱方(1974-),男,工程师,硕士,研究方向:无线电物理;甘宸伊(1985-),男,工程师,硕士,研究方向:数字图像处理、航空测控。
TN958.96
A
1009-0401(2017)01-0013-04

