改进的磁源体边界识别方法

张 琪， 张英堂， 李志宁， 范红波

(陆军工程大学石家庄校区车辆与电气工程系， 河北 石家庄 050003)

边界识别是磁异常数据解释的重要组成部分,其中单个磁源体的边界描绘方法有解析信号模的极大值[1]、水平导数的极大值[2]和垂向导数的零值[3]等。但当存在多个不同埋深的磁源体时，深部弱异常体的磁异常往往会被浅部强异常体所掩盖，难以同时描绘各磁源体的边界。倾斜角法[4-6]和Theta图法[7-8]虽然能够描绘不同埋深的磁源体的边界，但识别结果趋于模糊、发散，限制了其进一步发展。场源体的边界可通过张量数据的特征值描绘，如：ORUC等[9]利用曲率重力梯度张量的最大特征值来解释Erzurum盆地的地质结构；ZHOU等[10]对其进行了改进，将重力异常数据结合到最大特征值公式中，以描绘具有正负重力异常场源体的边界。然而，与重力异常简单的对应关系不同，磁异常对磁化方向十分敏感，这给准确识别磁源体的边界增加了难度。

鉴于此，笔者首先利用化极算法消除斜磁化带来的不利影响，然后采用基于曲率磁梯度张量矩阵的最大特征值的归一化改进算法，提取得到多个磁源体的特征边界等值线，最后通过对离散的边界等值点进行最小二乘拟合，得到最接近磁源体真实边界的连续曲线。

1 边界识别理论

1.1 磁梯度张量

磁梯度张量表示磁场三分量在三个互相正交方向上的空间变化率，其矩阵形式为

(1)

式中：G为磁梯度张量矩阵；Bi(i=x,y,z)为磁场矢量；Bij(i,j=x,y,z)为磁梯度张量分量。

1.2 曲率磁梯度张量

曲率磁梯度张量矩阵C为

(2)

求解其特征值矩阵，可得

(3)

(4)

式中：λ1和λ2分别表示曲率磁梯度张量矩阵的最大特征值和最小特征值。

在此基础上，笔者提出了基于曲率磁梯度张量矩阵的最大特征值的归一化改进算法，并将其定义为λ，其表达式为

(5)

式中：λ1_max为λ1的最大值;k1的取值为0.001～0.1。

1.3 倾斜角法

倾斜角是位场总水平导数和垂向导数比值的反正切函数，其零值等值线可突出场源体的边界特征。张双喜等[6]对倾斜角进行了改进，将改进形式定义为T1，其表达式为

(6)

式中：U为磁标量势。

将式(6)拓展成张量形式，并定义为T2，其表达式为

(7)

将增强型倾斜角定义为T3，其表达式为

(8)

式中：k=min(|Bz|)/max(Bzz)

1.4 Theta图法

Theta图法的最大值等值线(趋近于1)可识别场源体的边界。对Theta图法进行改进[5]，得到4种改进形式，将其依次定义为θ1、θ2、θ3和θ4，其表达式分别为

(9)

(10)

(11)

(12)

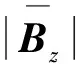
1.5 最小二乘法

受实际探测方式的影响，利用实测磁异常数据计算得到的边界等值线通常由一系列离散的边界等值点组成，其离散性特点给磁异常数据的解释增加了困难。最小二乘法[11]是一种常见的拟合方法，最小二乘解是在假设测量点产生的随机误差为正态分布的前提下，采用最大似然估计法得到的一个最优估计解，该解使得测量误差的平方和最小,因此可采用最小二乘法对离散等值点进行拟合，以求解得到最接近磁源体边界轮廓曲线，进而利用拟合曲线及其参数对磁源体的水平分布范围做出定量推断。

由于水平放置的规则长方体和圆柱体等磁源体的特征边界等值线的形状非常接近椭圆，因此可对其进行最小二乘椭圆拟合。其基本过程为：首先假设椭圆参数，然后计算每个待拟合点到该椭圆的误差距离的平方和，最后求出使该平方和最小的椭圆参数。

2 仿真分析

针对磁性组合体模型进行一组试验。由长方体(目标1)、正方体(目标2)和圆柱体(目标3)构成的磁性组合体模型及其真实边界位置如图1所示，其几何参数如表1所示。磁性组合体的磁化强度为30 A/m，磁倾角为56°，磁偏角为-16°。网格大小为121×121，水平方向上的采样间隔为1 m。

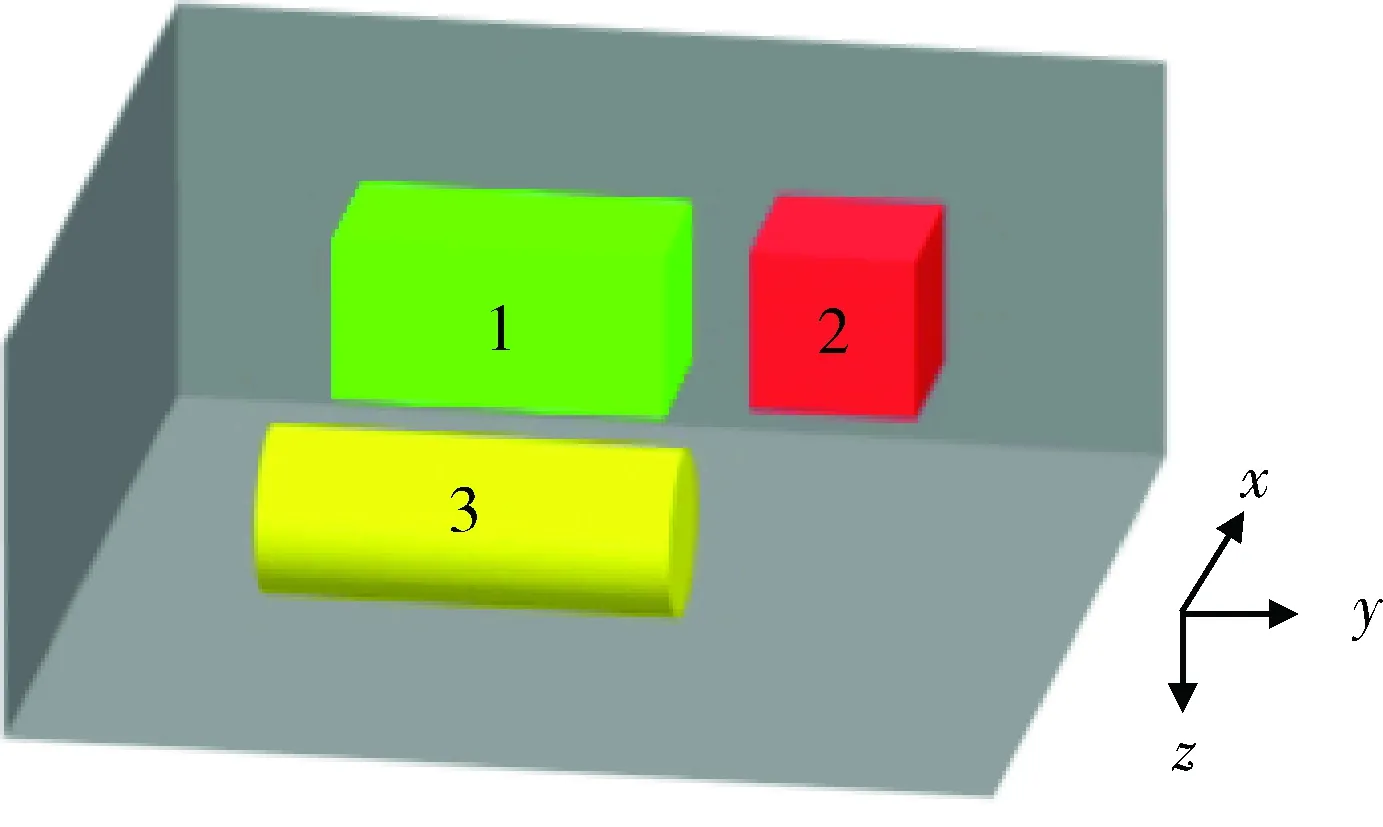
图1 磁性组合体模型及其真实边界位置

目标中心坐标/m轴向长度/mxcyczcxayaza130-101620402021030142020203-25-518205020

为了消除斜磁化给边界识别结果带来的不利影响，首先对磁总场强度(Total Magnetic Intensity, TMI)数据进行化极处理。磁性组合体的化极TMI和特征边界等值线的计算结果如图2所示，可以看出化极TMI和特征边界等值线与磁性组合体真实边界位置的对应关系良好：λ、T1、T2、T3的零值等值线识别效果较好，基本能够突出磁性组合体的边界位置；θ1、θ2、θ3、θ4的边界等值线识别效果较差，其中θ1、θ2、θ3的识别结果出现了假边界，而θ4的识别结果由一系列封闭圆环组成，辨识度较差。

为了使仿真更加真实，向TMI数据中加入幅值为TMI最大值1%的高斯白噪声，磁性组合体的化极TMI和特征边界等值线的计算结果如图3所示。可以看出：受噪声干扰的影响，T2、T3、θ1、θ2、θ3、θ4识别结果的信噪比较低，辨识度较差；λ和T1受噪声干扰的影响较小，其中λ的识别结果较准确，T1的识别结果较发散。

图2 磁性组合体的化极TMI和特征边界等值线

结合图2、3可知：基于曲率磁梯度张量矩阵的最大特征值的归一化改进方法受噪声干扰的影响较小，其零值等值线更接近磁源体的真实边界轮廓，识别精度更高。

为了进一步提高边界识别精度，将图3(b)中λ的零值等值线作为待拟合对象，对其进行滤波处理，然后对离散的边界等值点进行最小二乘椭圆拟合，最终得到的磁性组合体边界轮廓拟合结果如图4所示，其拟合所得椭圆的几何参数如表2所示。

由图4可以看出：最小二乘拟合结果能够直观地描绘磁性组合体的边界，且与其真实边界轮廓的吻合度较高。对比表1、2可知：拟合所得椭圆的中心坐标、长轴和短轴与磁性组合体的实际边界尺寸基本一致，且椭圆长轴的旋转角为判断磁源体的走向提供了近似参考。由此可以得出结论：最小二乘拟合结果能够通过定量描绘磁源体的边界特征提高边界识别结果的精度。

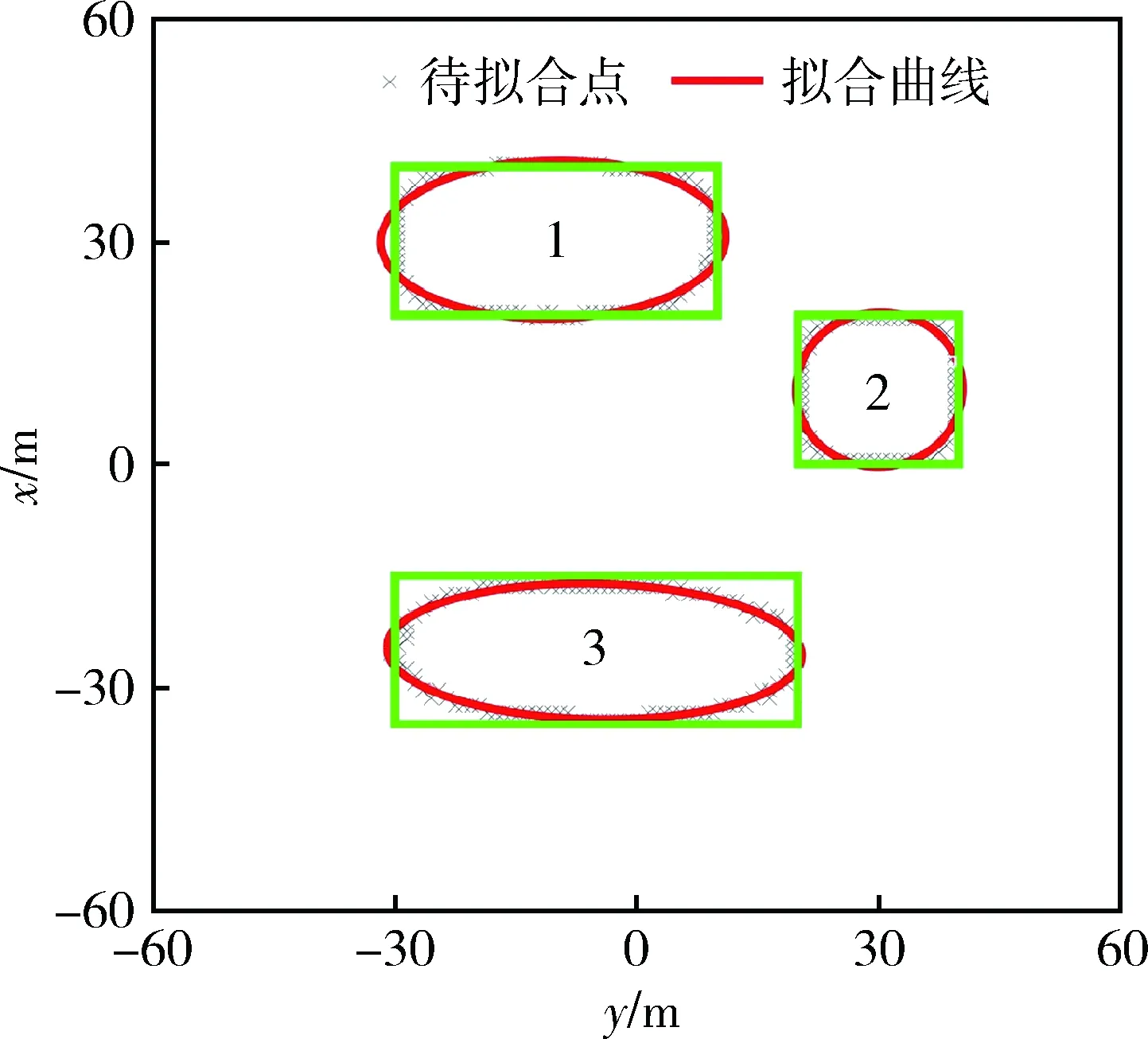
图4 磁性组合体的边界轮廓拟合结果

目标中心坐标/mxcyc长轴2a/m短轴2b/m旋转角θ/(°)130．21-10．3542．821．281．21210．0230．1120．9420．6151．683-25．74-5．2751．4718．251．3

3 实例验证

为验证上述方法的实际应用效果，在某2.1 m×2.1 m的测区内分别放置一个圆筒(目标1)和一个圆盘(目标2)进行探测试验，如图5所示。设观测面的z坐标为0，则圆筒的中心坐标为(1.28,0.63,0.4)，母线和直径长度分别为0.46、0.11 m；圆盘的中心坐标为(0.43,1.45,0.6)，母线和直径长度分别为0.1、0.33 m；网格大小为22×22，水平方向上的采样间隔为0.1 m；测区的地磁场倾角为56°，地磁场偏角为-16°。

对实测TMI数据进行化极处理，化极TMI和特征边界等值线的计算结果如图6所示。可以看出：

图5 圆筒和圆盘的探测试验

T2、T3、θ2、θ3的边界等值线能够大致描绘出磁源体的轮廓，但识别结果较发散；T1、θ1、θ4的识别结果更发散，已严重干扰真实边界的辨别：相比之下，λ的识别效果最好，其零值等值线与实际模型真实边界轮廓的吻合度较高。因此，可将λ的零值等值线作为边界拟合对象。

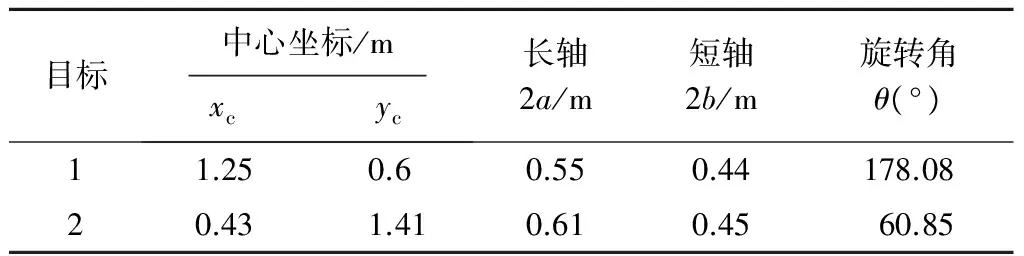
为了提高识别精度，首先对图6(b)中λ的零值等值线进行滤波处理，然后利用最小二乘法对其进行拟合，最终得到圆筒和圆盘的边界拟合结果如图7所示，拟合所得椭圆的几何参数如表3所示。

图6 实际模型的化极TMI和特征边界等值线

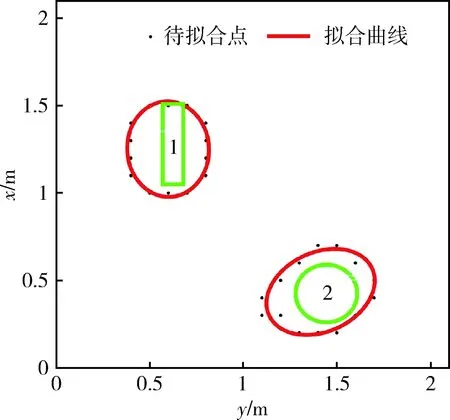
图7 圆筒和圆盘的边界拟合结果

目标中心坐标/mxcyc长轴2a/m短轴2b/m旋转角θ(°)11．250．60．550．44178．0820．431．410．610．4560．85

根据图7和表3可知：拟合所得椭圆的中心坐标、长轴和短轴等参数与实际模型大体吻合，椭圆长轴的旋转角为判断实际模型的走向提供了大致参考，这在一定程度上提高了边界识别结果的准确度。

4 结论

最小二乘拟合结果为判断磁源体的中心位置、水平分布范围和大致走向等提供了定量参考，提高了边界识别结果的准确度，可用于靶场中地雷和未爆弹的型号判断，海洋环境中潜艇、水雷和地下管道的轮廓识别以及油气矿产的勘探范围估计等。但受测量误差等因素的影响，最小二乘拟合结果与实际磁源体模型的真实边界仍存在一定误差，下一步将围绕磁源体的三维反演展开研究。

[1] NABIGHIAN M N.The analytic signal of two-dimensional magnetic bodies with polygonal cross-section:its properties and use for automated anomaly interpretation[J].Geophysics,1972,37(3):507-517.

[2] 王万银.位场总水平导数极值位置空间变化规律研究[J].地球物理学报,2010,53(9):2257-2270.

[3] WANG W,PAN Y,QIU Z.A new edge recognition technology based on the normalized vertical derivative of the total horizontal derivative for potential field data[J].Applied geophysics,2009,6(3):226-233.

[4] MILLER H G,SINGH V.Potential field T：a new concept for location of potential field sources[J].Journal of applied geophy-sics,1994,32(2/3):213-217.

[5] 马国庆,黄大年,于平,等.改进的均衡滤波器在位场数据边界识别中的应用[J].地球物理学报,2012,55(12):4288-4295.

[6] 张双喜,张青杉,陈超,等.利用磁异常模量进行磁性体边界检测[J].地质与勘探,2015,51(6):1025-1032.

[7] WIJNS C,PEREZ C,KOWALCZYK P.Theta map:edge detection in magnetic data[J].Geophysics,2005,70(4):L39-L43.

[8] 邰振华.位场数据高精度处理方法的研究与应用[D].长春:吉林大学,2016.

[9] ORUC B,SERTCELIK I,KAFADARÖ,et al.Structural interpretation of the Erzurum basin,eastern Turkey,using curvature gravity gradient tensor and gravity inversion of basement relief[J].Journal of applied geophysics,2013(88):105-113.

[10] ZHOU W,DU X,LI J.The limitation of curvature gravity gradient tensor for edge detection and a method for overcoming it[J].Journal of applied geophysics,2013(98):237-242.

[11] FITZGIBBON A,PILU M,FISHER R B.Direct least square fitting of ellipses[J].IEEE transactions on pattern analysis and machine intelligence,1999,21(5):476-480.