基于聚类分析方法的多准则ABC库存管理

龙小波

摘 要：企业通常将库存元件进行分类来达到高效库存管理的目的，广泛应用于库存分类的方法就是ABC分类法。在多准则分类方面，有很多对准则权重如何产生的研究，但是很少有对决策矩阵变换方法的研究。近年来出现了一些将聚类分析方法用于ABC库存分类的案例，但是他们的方法过于复杂。文章提出了一种新的决策矩阵变换方法，该方法使规范后的决策向量均值相等，并将一种简单的聚类分析方法应用于ABC库存分类中。在文章最后用一个案例来说明该方法的有效性。

关键词：多准则决策；ABC库存分类；聚类分析；均值变换

Abstract： Companies often classify inventory components into several groups to achieve the purpose of efficient inventory management. What is widely used in the inventory classification is the ABC classification. In terms of a multi-criteria classification， there are a lot of researches on how to get criteria weights， but few study on decision matrix transform method. In recent years， there have been some clustering analysis methods are used in ABC classification， but they are too complicated. This article puts forward a new method of decision-making matrix transformation. The method makes the average of the decision vector equals after the specification. We also applied a simple cluster analysis method to the ABC inventory classification. At last， a real-world example is included to illustrate the proposed approach and it advantages.

Key words： multi-criteria decision making； ABC inventory classification； clustering analysis； average conversion

引 言

企业需要对大量的库存元件进行管理，库存管理费用也是占据企业成本的很大一部分。为了提高企业的竞争力，企业需要找出科学的、合理的库存管理方案来对库存元件进行管理。库存管理方面有很多问题，例如库存预测、库存分类、库存控制策略的选择和优化以及其他的辅助策略。库存分类是高效管理企业库存元件的关键的一步，广泛使用于库存分类的一种方法是ABC分类法。ABC分类法是一种基于帕累托准则的分类方法。它是一种简单的、广泛被接受的、科学的库存管理方法。

传统的ABC分类方法基于年使用费用来进行分类，年使用费用是年使用数量与元件单价的乘积。一般地，A类元件在数量上很少，但是却占据很大的年使用价值；C类元件在数量上很多，但是只占很少的年使用价值；介于A类元件与C类元件之间的就是B类元件。在库存控制策略上，A类元件需要重点关注，循环盘点来提高库存精度；B类元件关注度次于A类元件，可以较长时间盘点一次；C类元件不需要太多关注，可以大量采购并储备较大的安全库存。

多准则库存分类（Multi-Criteria Inventory Classification，MCIC）的研究在过去的20年中已经有很多。我们常用层次分析法来求各准则权重，然后对各准则加权求和的方法解决MCIC问题，加权后得出一个总评分，作为多准则ABC分类的依据。文献[1]采用了K-means算法对ABC分类进行优化，文献[2-3]采用了模糊聚类分析方法来对库存元件进行分类，但是他们都没有提出一种能针对多准则总评分的聚类方法。为此，本文提出对决策矩阵的变换方法的改进，采用一种均值变换方法，使变换后的决策矩阵各准则向量的均值相等且都等于1。然后，本文对加权后的总评分采用一种聚类分析的方法进行库存元件的ABC分类，文章详细介绍了该聚类分析方法的步骤，并用一个案例来说明该方法的有效性并做了简短的总结和评价。

1 基于聚类分析的ABC库存管理方法

在进行多准则库存分类的时候需要解决几个问题。第一个，决策矩阵数据的规范化，文章采用了均值变换法，将在1.1中说明；第二个，准则权重的获取，本文主要是针对AHP这种主观权重获取方法来说，AHP方法的具体步骤参考文献[4]；第三个，根据元件加权后的总评分，如何进行ABC分类，文章采用了一种简单聚类分析的方法，具體步骤将在1.2中说明。

1.1 决策矩阵的规范化

假设有n个待分类的元件，每个元件有m个准则，令a表示第i个元件在第j个准则下的评分。这样就得到了原始决策矩阵A=a。由于各准则数据的单位不同，我们要对不同量纲的各准则数据进行规范化来消除量纲的影响。通常a被规范化为0，1之间，规范化后的决策矩阵B=b。但是，这种变换使得不同准则下的b的均值各不相同。为了改进这个缺点，文章提出一种均值变换方法，具体变换公式如下：

已知决策矩阵A=a，下面的均值变换方法将A转化为规范化的决策矩阵B=b。

其中：

其中，u，a和a可以由下面公式給出：u=averagea，a，…，a， j=1，2，…，n； a=maxa，a，…，a， j

=1，2，…，n； a=mina，a，…，a， j=1，2，…，n。

这样的均值变换将各准则放到同一个水平，用AHP求出的权重才有意义，得出的加权后的综合评分就能真实反映出各个元件的重要性。

1.2 一种聚类分析方法应用于ABC库存管理

令w表示第j个准则对应的权重大小，则：

文献[5]提出了一种简单的聚类分析方法，这种方法可以将一组数据根据其数值大小将其分为两组，相当于通过聚类分析将其分为两类。这种方法可以用于ABC分类中，综合评分y，1≤i≤n就是一组数据，可以先用该聚类分析方法分出C类，再对剩下数据再用一次该聚类分析方法分出B类和A类。具体步骤如下

首先，将数组y，1≤i≤n按升序排列得到新的有序数组为0≤x≤x≤…≤x；

再令S=x/x，进而计算下面两组数据的均值：

最后，画出S分别与Lx和Lx的曲线，两条曲线会有一个交点，该点就是聚类分析的临界点。需要注意的是使用的聚类分析方法只是针对数据的分类方法，可能会和ABC原理有冲突，所以在具体分类的时候需要结合ABC原理进行适当的调整。一般地，A类元件数目占总数的5%～15%，B类元件数目占总数的20%～30%，C类元件数目占总数的60%～80%。

2 案例分析

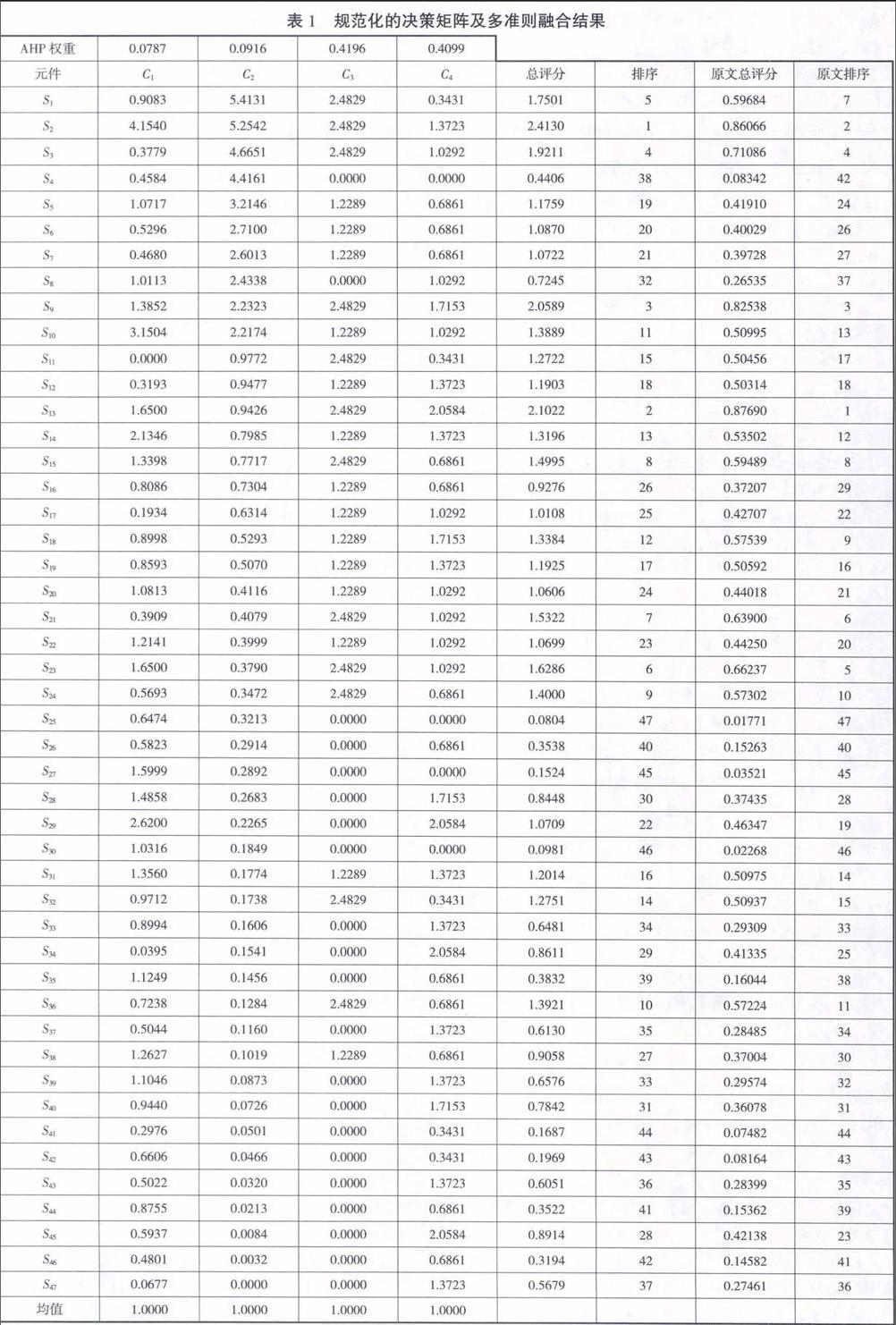
某企业要将47个备件进行分类，原始数据来源于文献[6]。FLORES等人使用了四个准则，分别是单价（美元）、年使用花费（美元）、关键性（1表示非常重要、0.01表示非常不重要、0.5表示一般重要）、采购时间（天），在本文中分别用C、C、C、C表示。FLORES等人采用AHP方法求出四个准则相对权重如表1第一行所示；文章采用均值变换的公式（1）来规范决策矩阵，如表1中第2～5列所示；再用公式（4）计算出总评分和相应的排序，如表1中第6～7列所示；原文的总评分和排序放在表1中最后两列。详细数据如表1所示。

从表1中可以看出，用均值变换规范后的决策矩阵各准则向量的均值都等于1，用AHP加权后的总评分和排序与用文献[6]相比有很大的差别。我们有理由相信，在案例中采用本文的均值变换规范后的决策矩阵使各决策向量的均值相等且等于1，再用AHP方法得出的权重加权后得出的总评分才能真正体现权重的意义。

这里，总评分就是本文聚类分析方法中的x。根据公式（5）至公式（7）得到的结果如图1所示：

根据聚类分析方法得到A、B、C三类的元件数如表2第二行所示，但是参考ABC分类原理后发现元件数占比很不合适，因此需要将图1中的第一条虚线调整到第二条实线处，这样就将C类元件分出来了。再将剩下的元件进行分类，分出B类元件和A类元件，再参考ABC分类原理，元件数占比合适，故不再调整。调整前后的元件分类个数如表2所示：

从表2中可以看出，本文使用的聚类分析的方法来作为A、B、C三类划分的依据，得到的调整后的分类结果是合理的，最后的分类结果与文献[6]对比如表3所示：

从表3中可以知道，由于决策矩阵变换方式不同，得到的元件的重要性就发生了变化，例如表3中36、10号元件（文献[6]中的B类元件）的重要性大于18号元件（文献[6]中的A类元件）。然后，文献[6]中的A、B、C三类元件数量是按照2∶3∶5来确定的，本文的分类结果是根据聚类分析方法结合ABC原理的方法得到的。本文从决策矩阵数据变换方法和ABC三类划分方法两个方面提出了改进，从而对多准则ABC分类的结果进行了优化。

3 结 论

本文对多准则决策方法中的决策矩阵数据变换方法进行了改进，提出了一种均值变换方法，该方法使变换后的各准则向量的均值相等且等于1，在采用AHP权重对决策矩阵加权后的综合评分才更能反映出元件真实的重要性，该决策矩阵变换方法适用于多准则决策问题。本文针对总评分采用了一种简单的聚类分析方法结合ABC原理作为ABC分类的边界划分的依据，对ABC分类方法提出了改进。最后将文章的结果与文献[6]中的结果对比，本文的结果与文献[6]的结果大体上一致，但是在排序和具体分类上面得到了优化。该方法还可以运用多准则领域的其他方面，同时，还需要更多的案例来验证该方法的优越性。

参考文献：

[1] 胡靖枫，何利力，周庆燕. 基于聚类分析的ABC库存分类方法研究[J]. 工业控制计算机，2015（3）：147-148.

[2] 李家驹. 模糊聚类分析在ABC库存管理中的应用[J]. 现代商业，2008（9）：142.

[3] 江玮璠. 基于模糊聚类分析的多准则ABC库存管理[J]. 物流技术，2009（1）：97-98，139.

[4] 樊于麟，李艳冰，徐克林. 基于层次分析法的刀具供应商选择[J]. 制造技术与机床，2016（3）：127-130.

[5] Jiang. R. Cluster analysis of maintenance management problems[C] // International Conference on Industrial Engineering and Engineering Management （IEEM 2009）， 2009.

[6] Flores BE， Olson DL， Dorai VK. Management of Multicriteria Inventory Classification[J]. Mathematical and computer modelling， 1992，16（12）：71-82.