一种三角函数权重的图像拼接算法
汪 丹,刘 辉,李 可,周 威
一种三角函数权重的图像拼接算法
汪 丹,刘 辉,李 可,周 威
(湖南师范大学 物理与信息科学学院,湖南 长沙 410006)
针对传统加权平均融合算法和渐入渐出融合算法仍然存在相对明显的拼接痕迹,提出一种三角函数权重的图像拼接算法。首先,对参考图计算图像重叠区域从左边界开始每一列像素所占重叠区的比例,将其用相应的角度表示;然后计算角度对应余弦值的平方,将此结果作为参考图的权重信息;对于目标图,计算靠近右边界的每一列所占重叠区的比例,并用角度表示,然后计算该角度对应正弦值的平方,将此结果作为目标图的权重;最后用计算得到的2个非线性的权重对两幅图进行图像拼接。实验结果表明无论摄像机是否在曝光差异较大情况下进行拍摄,改进的图像融合算法效果更好。
加权平均融合;渐入渐出融合;三角函数;权重;图像融合;曝光差异
0 引言
图像融合是指将多张在同一时间(不同时间)获取的关于某个场景的图像序列信息加以综合,生成一个新的完整的关于此场景的解释。图像融合技术主要用于虚拟现实技术VR(virtual reality)[1]之中,作为静态图像拼接、视频图像实时拼接[2]后至关重要的一步,融合质量的好坏对结果有很大影响。
目前为止,国内外学者提出了很多图像融合算法。国外近几年主要针对多光谱、多视点图像融合[3]进行研究。提出了基于向导滤波的方法[4]、从原图中提取感兴趣区域的方法[5]、基于EOL的加权平均算法[6]、可见光谱下多分辨率变换算法[7]等融合算法。传统的加权平均融合算法[8],简单易懂,但因为权重是固定的,拼接缝隙比较明显,融合效果相对较差;渐入渐出融合算法[9]采用基于距离变换的权值,使图像在重叠区域有一种渐变效果,过渡相对自然,现实中这种融合算法应用比较广泛,但仍然存在肉眼可见的拼接缝隙;最佳缝合线算法[10]是一种利用动态规划的思想减小融合中“鬼影”以及重影问题的算法,但计算量相对较大,曝光差异较明显。多分辨率融合是将待拼接图像分解成一系列拉普拉斯图像金字塔,相对麻烦。
本文在渐入渐出融合算法前提下提出一种基于三角函数权重的拼接算法,通过计算每一列与角度的关系,将每一列用角度表示,计算其余弦值的平方作为权重,计算复杂度低。
1 图像拼接
进行图像融合之前需要先进行图像拼接,图像拼接是将一组相互之间存在重叠区域的图像序列进行空间匹配,经过重采样融合后形成一幅包含各图像序列信息的宽视角场景的、完整的、高清晰的新图像的技术。
以图1中2幅图像A、B的拼接为例,基本步骤如下:①将实景图A、B分别投影到柱面,统一坐标系;②利用SIFT[11]、SURF[12]等算法(本文选用SIFT算法)进行特征点检测,然后进行特征点匹配得到匹配对信息;③由特征点匹配对信息计算出两幅图的变换矩阵,得到两幅图的空间变换关系;④以实景图A为参考图,对实景图B进行矩阵变换,即完成图像拼接。

图1 实景图
对实景图A、B经过柱面投影、SIFT特征点检测和匹配、计算矩阵以及进行矩阵变换后,拼接结果如图2所示,从图中可以看到明显的拼接痕迹,需要有效的图像融合算法来消除。

图2 图像拼接结果
2 渐入渐出融合算法
融合主要是处理图像拼接所产生的痕迹,使边界部分过度自然平滑。在重叠区域,渐入渐出融合算法[13]主要是使权重按式(1)随着像素点位置的变化而呈线性变换,以此实现平滑过渡,提高图像融合质量:
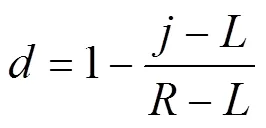
式中:是像素点的列数;、分别是重叠区域的左、右边界。
按照式(1),实景图A、B的权重变化如图3所示。
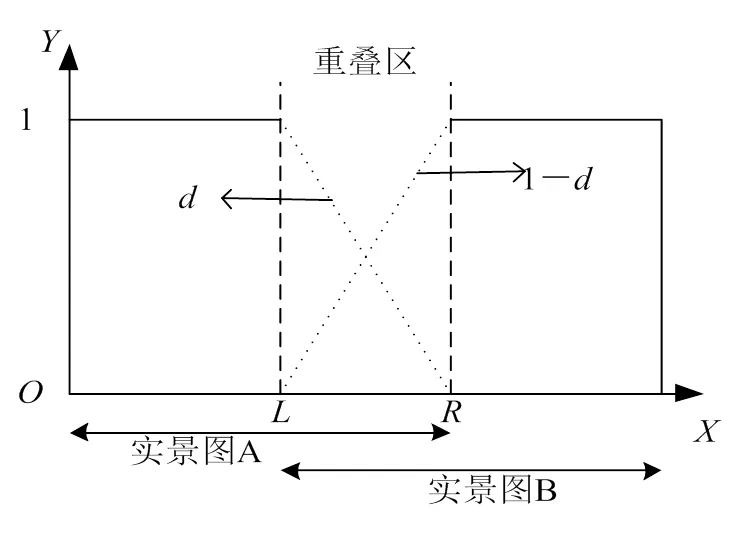
图3 渐入渐出融合权重变化图
按照图3进行融合后,重叠区域像素点的灰度值可以按式(2)计算:
(,)=×(,)+(1-)×(,) (2)
当A、B为真彩图时,3个颜色通道分别按照式(2)计算即可。
3 三角函数权重融合算法
3.1 理论分析
在渐入渐出融合算法前提下,提出一种三角函数权重的融合算法,首先把每列像素点按照式(3)用角度表示:

计算可知的取值范围在区间[0,p/2]。
然后,按照式(4)和式(5)求参考图和目标图的权重,两个权重满足式(6)的要求:
=cos2() (4)
=sin2() (5)
cos2()+sin2()=1 (6)
最后求融合后像素点与实景图A、B的关系,如下式:
(,)=×(,)+×(,) (7)
如果是真彩图像,分别对3个颜色通道运用式(7)即可。由式(3)、(4)可以得权重随着位置变化的关系:

两个权重随像素位置变化的关系如图4。
对比图3和图4,可以直观地看到,本文算法的权重从2个边界向中心逼近时变化非常平缓。而图像融合算法通常是权重随着像素位置变换越缓慢越好,表示图像过渡得越自然。为了从理论上分析本文算法与渐入渐出融合算法的优劣,选用权重对位置的导数来衡量。式(9)是基于三角函数的权重随位置变化的快慢关系式,式(10)是渐入渐出融合算法中权重随位置的快慢变化关系:
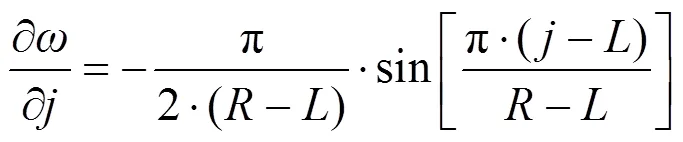

比较式(9)、(10)得出的只是两种方法在任何一个像素点时权重的瞬时变化率。即当像素点靠近边界,即拼接痕迹时,本文算法得到的权重比渐入渐出算法变化小很多,即在边界处,本文算法减少甚至消除痕迹的效果更明显。为了比较总的变化率,采用下面两式对两种瞬时变化率求积分即可:


由上面两式可以看出,两种方法在重叠区域的总变化率是相同的。即本文算法在处理边界痕迹时效果更好,同时总的变化率又不会比渐入渐出融合算法大。
3.2 实验结果
本算法均在Window 7操作系统上利用Visual Studio 2013结合OpenCV库函数实现。图5分别是传统加权平均融合算法[14]、渐入渐出融合算法和本文算法的融合结果。
由图5看出,加权平均融合算法效果较差,拼接痕迹非常明显;而渐入渐出融合算法融合效果已经比较好,基本能满足实验要求,但划线部分仍存在拼接缝隙;本文算法的融合效果已经几乎看不出拼接痕迹。图5(b)和(c)的融合效果依靠肉眼可能看不出特别明显的差别,这就需要统计图像评价指标的数据。

3.3 曝光差异下的图像融合比较
图1中的两幅图是在正常光线下拍摄的实景图,但有时候当摄像机平移或者旋转时,自动或手动选取的曝光系数可能不同,即两幅图的曝光差异可能很大。如图6中的两幅图所示,实景图C很亮,而实景图D很暗。

图6 曝光差异下的实景图
一般情况下,为了得到较好的视觉效果,当待拼接实景图出现曝光差异很大时,先要进行亮度调整然后再进行拼接、融合。为了比较本文所述算法的有效性和先进性,在此不进行亮度调整而是直接进行拼接。
图7给出了加权平均融合算法、渐入渐出融合算法、三角函数权重融合算法处理后的效果图。

图7 图6经3种算法融合后的效果图
从图7看出,在曝光差异很大的情况下,加权平均融合算法对拼接产生的痕迹只有轻微的减弱作用;渐入渐出融合算法虽然已经减轻了拼接痕迹的影响,但仍然可以看出融合不自然。三角函数权重融合算法在很大程度上已经消除了拼接痕迹,而且较好地处理了边界突兀的问题,使图像过度部分较为平滑,已经能满足实验要求。
3.4 评价指标
为了从数据上比较传统加权平均算法、渐入渐出算法和三角函数权重拼接算法的优劣,而一个指标通常不能进行客观而全面的评价,故现从信息量、统计特性和信噪比3个方面来评价图像融合的效果[15-17]。选用基于信息量的指标:信息熵;基于统计特性的指标:均方根误差(RMSE);基于信噪比的指标:峰值信噪比(PSNR)。结果如表1所示。
由表1可知,无论有没有曝光差异,利用本文算法进行图像拼接后的信息熵更大,即图像信息量更丰富;PSNR较高,即噪声得到了有效抑制;RMSE较小,也证明图像误差较小。综合各项客观指标,与传统加权平均融合算法和渐入渐出融合算法对比下,本文算法确实是有优势的。后续如果能将这种算法进行优化用在多幅复杂图像的拼接或者视频图像实时拼接中,累积优势会更明显。

表1 3种算法融合结果对比
4 结论
对于渐入渐出融合算法仍然存在细微的拼接缝隙问题,提出了一种基于三角函数权重的拼接算法,原理相对简单,计算量较小,运行速度快,有效减少了拼接痕迹,改善了图像融合的效果。后续的工作主要是针对重叠区域融合后出现的重影、“鬼影”问题进行研究和改进。
[1] 赵书睿. 全景图像拼接关键技术研究[D]. 成都: 电子科技大学, 2013.
ZHAO Shurui. The key technology of panorama mosaic[D]. Chengdu: University of Electronic Science and Technology of China, 2013.
[2] 任超锋. 航空视频影像的正射影像制作关键技术研究[D]. 武汉: 武汉大学, 2014.
REN Chaofeng. Research on key technologies of DOM generation by aerial video[D]. Wuhan: Wuhan University, 2014.
[3] Gangapure V N, Banergee S, Chowdhury A S. Steerable local frequency based multispectral multifocus image fusion[J]., 2015, 23: 99-115.
[4] Li S T, Kang X D, Hu J W. Image fusion with guided filtering[J]., 2013, 22(7): 2864-2875.
[5] Li S T, Kang X D, Hu J D, et al. Image matting for fusion of multi-focus images in dynamic scenes[J]., 2011, 14: 147-162.
[6] Benes R, Dvorak P, Faundez-Zanuy M, et al. Multi-focus thermal image fusion[J]., 2012, 34: 536-544.
[7] Li S T, Yang B, Hu J D. Performance comparison of different multi-resolution transforms for image fusion[J]., 2010, 12: 74-84.
[8] 张欣. 全景拼接的关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2009.
ZHANG Xin. Research on the key technology of panorama mosaic[D]. Harbin: Harbin Engineering University, 2009.
[9] 郭晶. 基于特征点的多幅图像拼接技术研究[D]. 西安: 西安科技大学, 2012.
GUO Jing. Multiple image stitching technique research based on the feature points[D]. Xi’an: Xi’an University of Science and Technology, 2012.
[10] James Davis. Mosaics of scenes with moving objects[C]//,, 1998: 354-360.
[11] Lowe D G. Distinctive image features from scale-invariant key points[J]., 2004, 60(2): 91-110.
[12] Herbert Bay, Tinne Tuytelaars, Luc Van Gool. Speeded up robust features[J]., 2006, 110(3): 404-417.
[13] 陆园园, 张明. 基于SIFT算法的红外图像拼接方法改进[J]. 计算机系统应用, 2015, 24(8): 165-170.
LU Yuanyuan, ZHANG Ming. Improved algorithm based on SIFT infrared image stitching algorithm[J]., 2015, 24(8): 165-170.
[14] 马杰. 360°全景图像拼接技术研究[D]. 成都: 西南财经大学, 2012.
MA Jie. Research on 360 degree panoramic image stitching. Chengdu: Southwestern University of Finance and Economics, 2012.
[15] 田霞. 混合粒子群优化算法在图像融合中的应用[D]. 西安: 陕西师范大学, 2009.
TIAN Xia. The application of hybrid particle swarm optimization in image panorama mosaic[D]. Xi’an: Shannxi Normal University, 2009.
[16] 袁金楼, 吴谨, 刘劲. 基于NSCT与DWT的压缩感知图像融合[J]. 红外技术, 2015, 37(11): 957-961.
YUAN Jinlou, WU Jin, LIU Jin. Image fusion based on compressed sensing of NSCT and DWT[J]., 2015, 37(11): 957-961.
[17] 王宇庆, 王索建. 红外与可见光融合图像的质量评价[J]. 中国光学, 2014, 7(3): 396-401.
WANG Yuqing, WANG Suojian. Quality assessment method of IR and visible fusion image[J]., 2014, 7(3): 396-401.
An Image Fusion Algorithm Based on Trigonometric Functions
WANG Dan,LIU Hui,LI Ke,ZHOU Wei
(,,410000,)
Many images stitching algorithms such as the weighted average image fusion and the gradual image fusion, could not make the stitching gap disappear. A new image fusion method based on trigonometric functions was proposed. Firstly, the overlap area ratio was calculated for each column of pixels, and was represented with corresponding angles. Then, the square of the cosine value was calculated, as weighted information of reference map. The square of the sine value was calculated as weighted information of target image. Finally, the two images are fused by using those two nonlinear weights.The experimental results show that the improved image fusion algorithm has better effects, whether or not the camera is operating in large exposure differences.
weighted average image fusion,gradual image fusion,trigonometric functions,weight,images fusion,different exposure index
TP399
A
1001-8891(2017)01-0053-05
2016-05-08;
2016-06-23.
汪丹(1992-),女,湖南常德人,硕士研究生,研究方向:鱼眼校正、图像拼接融合、全景漫游。
刘辉(1964-),女,湖南汉寿人,硕士,副教授,研究方向:图像处理、信号处理。E-mail:liuhui1366@126.com。

