基于GM－BP神经网络的地方政府债务风险预警系统研究——以2015年重庆市38区县样本数据为例

马恩涛，吕函枰

(山东财经大学财政税务学院，山东济南 250014)

基于GM－BP神经网络的地方政府债务风险预警系统研究
——以2015年重庆市38区县样本数据为例

马恩涛，吕函枰

(山东财经大学财政税务学院，山东济南 250014)

以2015年重庆市38个区县的债务数据作为研究样本，利用灰色关联方法(GM)与BP神经网络两种理论在非线性处理方面的优势，构建了基于GM－BP神经网络的地方政府债务风险预警系统，并运用该预警系统对重庆市各区县债务风险进行了实证分析。结果表明:2015年重庆市33个区县债务风险处于绿色可控区，4个区县(大渡口区、开县、南川区、潼南区)处于橙色预警区，1个区县(城口县)债务风险处于红色风险区，重庆市地方政府债务风险总体可控；并且，与未经约简的BP神经网络预警系统相比，GM－BP神经网络预警系统的训练时间更短，预警准确性更高，在结合预警地区的实际情况做出微调后，其更具有一定的普适性。

灰色关联方法；BP神经网络；地方政府债务风险；预警系统

0 引 言

自2008年美国次贷危机发生以来，中国政府的债务问题越来越受到国内外相关机构和学者的重视。2016年5月10日，作为国际三大评级机构之一的穆迪(Moody’s)认为中国债务占GDP的比重已经增加至280%左右且面临严峻的或有债务上升风险。而中国社科院李扬团队编制的中国政府资产负债表显示中国的整体债务增长过快:2008年到2014年中国经济整体债务占GDP的比重从170%上升至235.7%，6年上升了65.7个百分点；而中国实体部门债务占GDP比重从2008年的157%上升到2014年的217.3%。中国杠杆率增长过快，需保持高度警惕。

鉴于中国日益严峻的债务形势，中国政府也开始高度重视地方政府债务风险问题。2014年，国务院印发《关于加强地方政府性债务管理的意见》(国发〔2014〕43号)，明确了全面规范地方政府性债务管理的制度设计和配套措施，标志着地方政府性债务管理进入全面改革的新时期。而2015年的“供给侧”改革所提出的去杠杆也是在去产能和去库存的基础上，结合国家给予的债务置换政策，采取“五挂钩、一甄别”的做法使地方政府的债务状况不再恶化，从而有效防范、化解金融风险。

在防范政府债务风险的过程中，国外一些发达国家所建立的债务风险预警系统由于翔实的预警指标、科学的预警区间以及良好的实施效果而受到越来越多发展中国家的关注和模仿，因此如何结合中国政府债务特征构建合理的地方政府债务风险预警系统进而正确认识中国地方政府债务风险状况并对其进行提前预警就显得尤为重要和紧迫。

1 文献综述

自20世纪80年代以来，随着世界范围内政府债务积累的日益严重，国内外学者开始研究债务风险问题。其中，不得不提到世界银行专家Hana所做的贡献。Hana[1]早在1998年所提出的财政风险矩阵即将政府债务根据其来源分为直接显性债务、直接隐性债务、或有显性债务和或有隐性债务，到现在还指导着我们的债务管理实践。我国政府近几年多次进行的政府债务统计，其统计口径和范围实际上就是借鉴了Hana的财政风险矩阵理论。Craig[2]把政府债务风险归因于或有债务偿还时间的随机性和作为担保的或有债务的潜在风险性。而Ricado等[3]以拉美国家政府债务危机为例，说明货币贬值同样可能诱发政府债务问题。同样，我国也存在政府债务风险问题。由于我国分税制体制的实行，政府债务风险问题尤其是地方政府债务风险已经严重威胁到中国经济的安全与稳定[4]。就我国地方政府债务风险成因而言，陈睿[5]认为导致地方政府债务风险的原因是财税体制不健全、政府过度举债；而孙浩颉[6]不仅将地方债务风险分为财政类、金融类和社会类三类，还进一步指出地方政府债务风险是由财权事权不匹配、考核体制片面化以及管理不当造成的。

在分析政府债务风险问题成因的基础上，国内外学者开始深入研究地方政府债务风险的防控，建立了一系列的地方政府债务风险预警系统。Smith[7]根据政府预期发债额运用计算机模拟仿真系统预测出相应的地方债务适度发行量，构建了地方政府债务仿真预警系统。与此同时，Ma[8]借鉴巴西的“地方政府借款限制”、美国的“地方财政监控计划及财政危机法”以及哥伦比亚的“交通信号灯”系统，设计了一套示范性的地方债务风险预警系统。在借鉴国外研究成果的基础上，根据我国特有的政治体制、历史背景，国内学者建立了符合我国国情的地方政府债务风险预警系统。刘尚希等[9]对新增债务压力进行了事前预警研究，开创了地方政府性债务风险预警领域动态研究的先河。之后裴育等[10]对地方债务风险状况进行描述，依据一定的标准量化了风险等级，并运用合成指数法和层次分析法构建了地方政府债务风险预警模型。洪源等[11]选取我国2007－2009年东、中、西部地区9个县的样本数据，构建了基于粗糙集－BP神经网络集成的地方政府债务风险非线性仿真预警系统。王振宇等[12]基于辽宁省的样本数据运用层次分析法(AHP)构建了一套可操作性、符合辽宁省省情的地方政府债务风险预警体系。朱文蔚等[13]采用因子分析法选取全国30个省市作为样本，对地方政府性债务风险进行评估及预警。

由于地方政府债务风险预警系统是一个包含多指标的复杂评估系统，彼此间存在非线性关系，因此单纯地采用因子分析法、聚类分析法等多元分析法准确度不高。而BP神经网络技术在灵活准确处理非线性数据方面具有独特的优势，可以解决学者们在建立地方政府债务风险预警系统中所遇到的准确度不高的问题。国内也有部分学者通过BP神经网络法对政府债务风险预警进行了研究，如邵伟钰[14]以江苏省2005年样本数据为例，在聚类分析法、因子分析法的基础上借助BP神经网络理论构建地方政府债务风险预警模型。刘骅等[15]运用K—均值聚类算法，并借助BP神经网络建立地方政府融资平台债务“风险阈”预警模型。

本文同样在吸收BP神经网络处理信息不完整数据时所具有高容错性优势的基础上，通过引入能够有效约简指标的灰色关联理论克服了其在建立地方债务风险预警系统中拓扑结构复杂、学习效率低、收敛速度慢以及易陷入局部极小状态的缺点，构建出了基于GM－BP神经网络并符合我国国情、能准确评估地方政府债务风险的预警系统。

2 地方政府债务风险预警系统构建

本文对地方政府债务风险预警系统的构建遵循以下几步:设计债务风险预警指标；划分预警指标的风险区间；确定债务风险预警系统方法。

2.1 地方政府债务风险预警指标设计

基于完备性、科学性、可操作性以及灵活性的原则，借鉴国内外研究成果，本文从系统论的思想出发，将影响地方政府债务风险的因素分为债务规模、宏观经济环境、政府偿债能力三个子系统，又将三个子系统分解为负债率、GDP增长率、公共预算收入增长率等九个指标。具体指标参见表1。

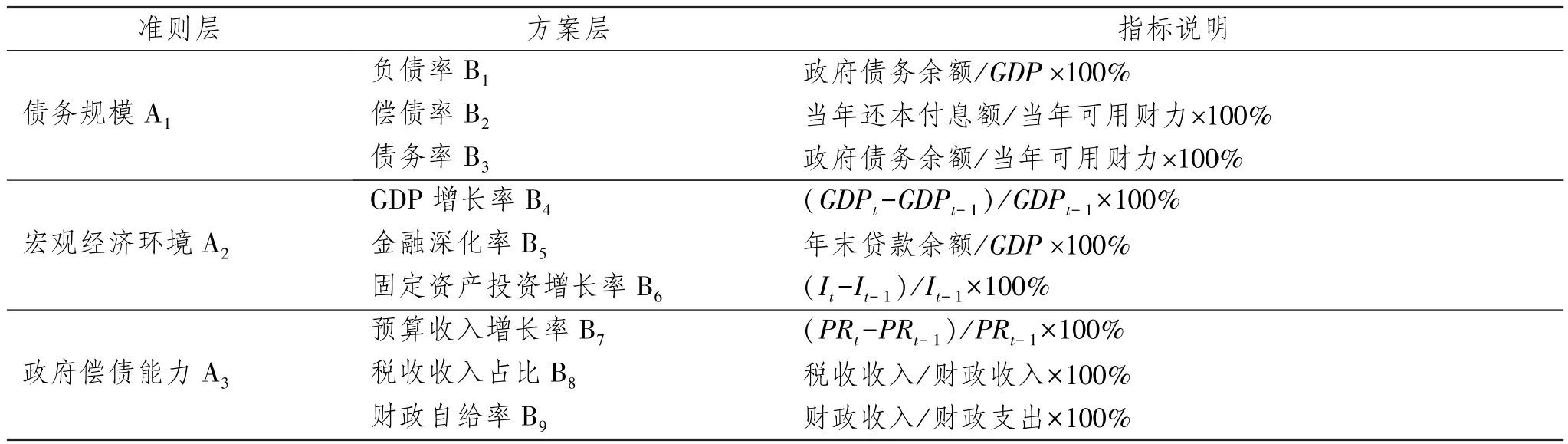
表1 地方政府债务风险预警指标设计

2.2 划分预警指标的风险区间

建立风险预警系统的关键是对各预警指标设置相应的风险区间，本文参照国际上通用的警戒线设置，在借鉴国内外已有研究成果并结合重庆市各区县地方政府实际情况的基础上，将各项指标风险区间划分为“红色风险区”“橙色预警区”和“绿色可控区”三个级别。同时，为了使各指标之间具有可比性与可观测性，将指标赋予相应的风险指数，并对各指标区间的设置做了明确说明。具体设置见表2、表3。

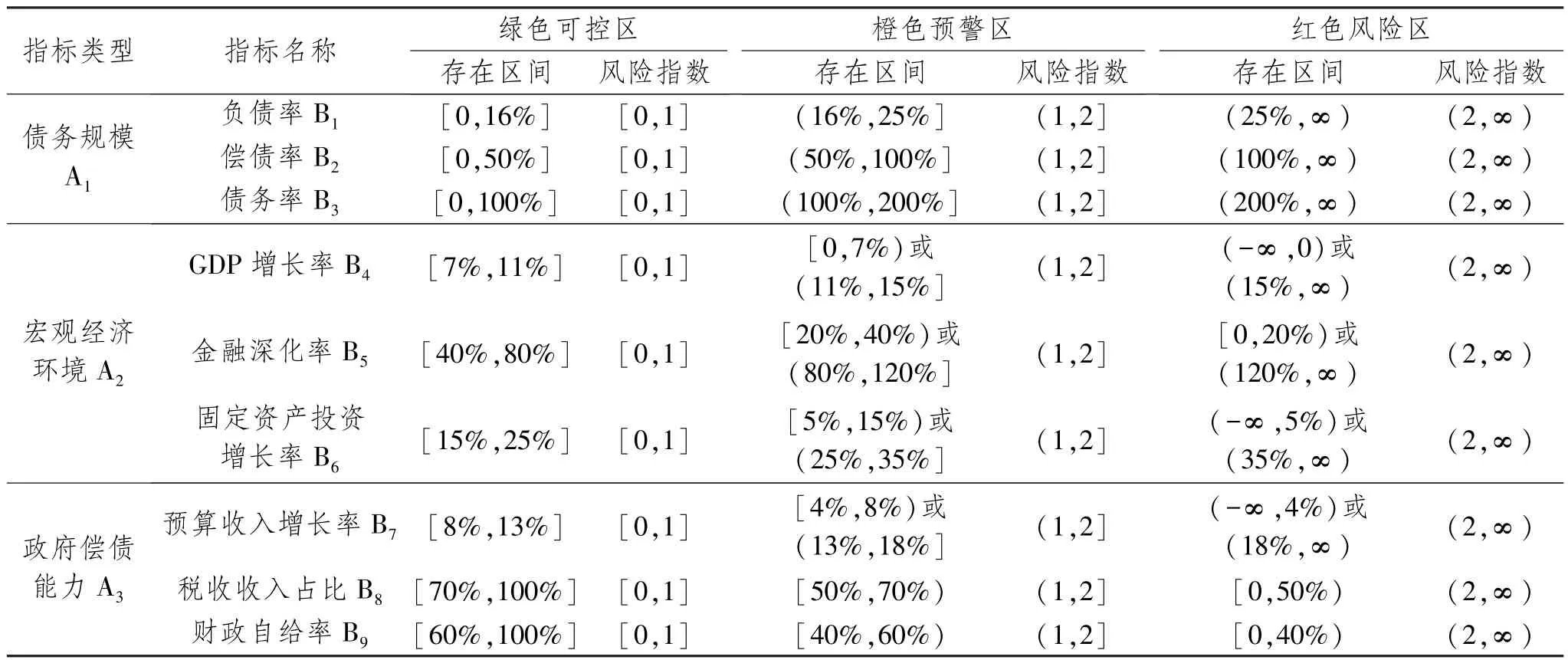
表2 地方政府债务风险预警指标的风险区间

表3 地方政府债务风险预警指标风险区间的设置依据

2.3 建立地方政府债务风险预警系统方法

地方债务风险预警系统是包含多指标的综合评价系统，常见的多元线性回归分析不能准确评估结果，必须运用多指标进行综合评价。本文采用新型人工智能方法，建立以灰色关联方法(Grey Model)和BP神经网络两种方法为核心的评估预测方法，构建符合我国国情的地方债务风险预警系统。

2.3.1 BP神经网络方法的基本原理

BP(Back－Propagation)神经网络是人工神经网络(Artificial Neural Networks，ANN)的一种，由于该网络具有计算量小、简单易行、并行性强等优点，是ANN中相对成熟且应用广泛的一种人工智能算法。它是一种按误差逆传播算法训练的多层前馈网络，即信号向前传播，误差反向传播。通过神经网络训练输出的误差来估计前导层的误差，层层前导，周而复始，不断学习训练下去，从而获得各层的误差估计。在此过程中根据预测误差反复调整网络权值和阈值，从而使BP神经网络预测的误差减小到可接受的程度。具体步骤如下:

①对数据进行归一化处理，归一于[－1，1]。

②网络初始化。给定输入输出序列(X，Y)，随机给定各连接层的权值ωij、ωjk和阈值a、b。定义输入层、隐含层和输出层的各神经元节点数分别为n、l和m，给定学习速率和神经元激励函数。

③确定隐含层。计算隐含层输出H的公式为:

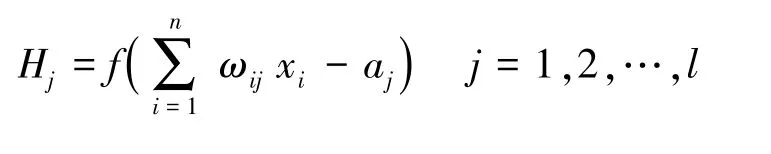
④确定输出层。计算输出层O的公式为:

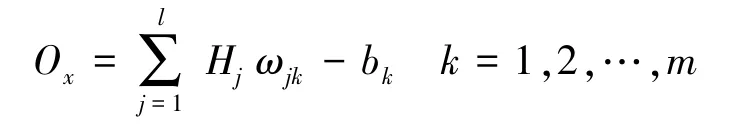
其中O为网络预测输出值。

⑤误差计算。计算均方根误差E的公式为:

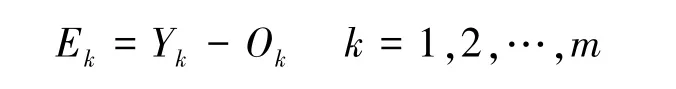
其中Y为期望输出值。

⑥权值更新。误差反向传播更新连接权值ωij、ωjk的计算公式为:

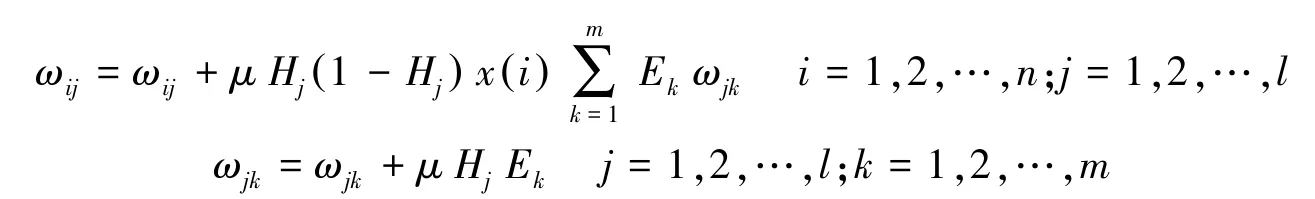
其中μ为学习速率。

⑦阈值更新。误差反向传播更新网络节点阈值a、b:

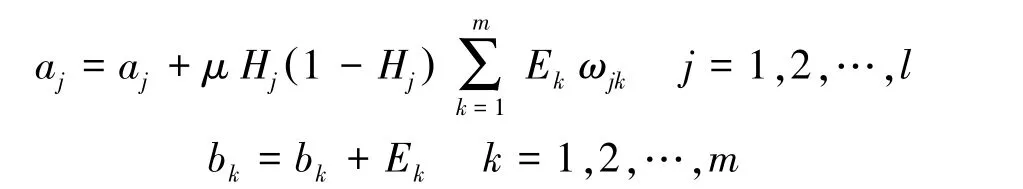
⑧检查是否达标，结束算法迭代，否则重复步骤③－⑦。

2.3.2 用灰色关联法(GM)约简预警指标

BP神经网络在实际的应用过程中，由于拓扑结构复杂，存在学习效率低、收敛速度慢以及易陷入局部极小状态的缺点。如果输入过多的参数，往往会导致迭代次数过多，计算精度下降。因此，本文用灰色关联法约简预警系统指标，从而减少输入参数，达到提高BP神经网络计算精度的目的。

灰色关联法的计算步骤如下:

①建立各相关指标的原始数据矩阵xi。

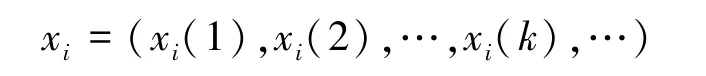
其中xi(k)表示i因素在第k年的原始数据。

②求初值化变换矩阵x′i。

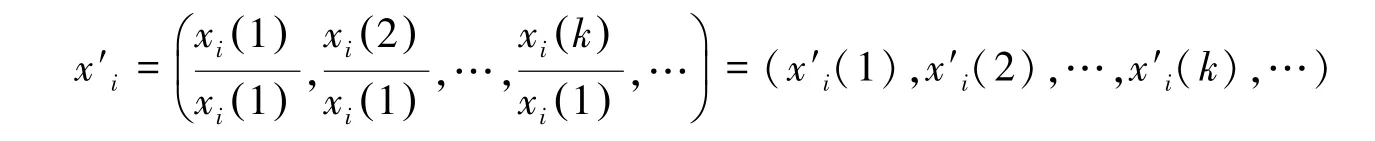
③求差序列Δ0i(k)。

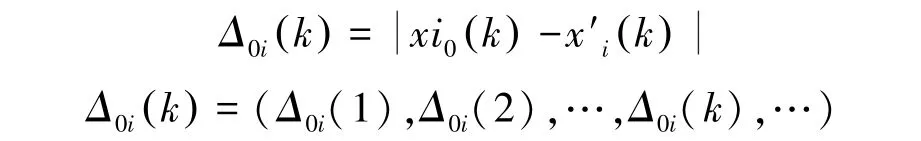
④计算关联系数ε0i(k)和灰色关联度γ0i。

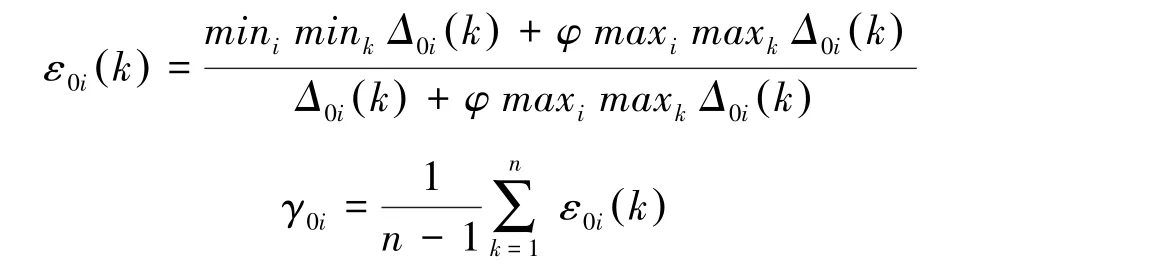
其中，φ为分辨系数，能够提高关联系数间的差异显著性，φ∈(0，1)，一般取φ＝0.5。ε0i(k)衡量xi对x0的影响程度，称之为xi与x0在k点处的关联度。

2.3.3 构建GM－BP神经网络模型

本文将灰色关联方法与BP神经网络两种人工智能方法糅合在一起，构建地方政府债务风险预警系统。具体构建思路如下:第一步，用灰色关联法约简预警指标，将九个指标通过灰色关联方法排序，剔除对预警系统影响最小的冗余指标。第二步，剩余关联度较大的指标作为BP神经网络的输入节点，通过多次训练学习确定隐含层节点，并且将综合评价结果作为输出节点。第三步，用样本数据对GM－BP神经网络进行训练和检验，从而构建出符合要求的实用性地方债务风险预警系统，实现风险预警的目的。

3 地方政府债务风险预警系统的实证分析

3.1 灰色关联分析

根据2013年12月30日审计署发布的《全国政府性债务审计结果》，我国省、市、县和乡镇各级政府负有偿还责任债务分别为17 780亿元、48 434亿元、39 573亿元和3 070亿元，分别占比16%、45%、36%和3%，市、县政府债务总额合计占全国政府债务的81%，因此选取县市区的数据样本更具有代表性。本文选取了2015年重庆市38个区县的数据作为样本数据，考虑到数据的可获得性，本文在“金融深化率”的求解过程中，采用了2014年的年末贷款余额与GDP的比值，其他数据均为2015年数据。数据来源于重庆市统计局、重庆市审计局网站，具有一定的可信度。

本文借鉴了曹明霞[16]的改进灰色关联度模型，该关联度能够反映序列间的正负相关关系，其结果可以为－1到1之间的数。只与序列的形状有关，与序列的相对位置无关。

运用Matlab8.1，编程计算样本数据求得各指标的关联度平均值如下:

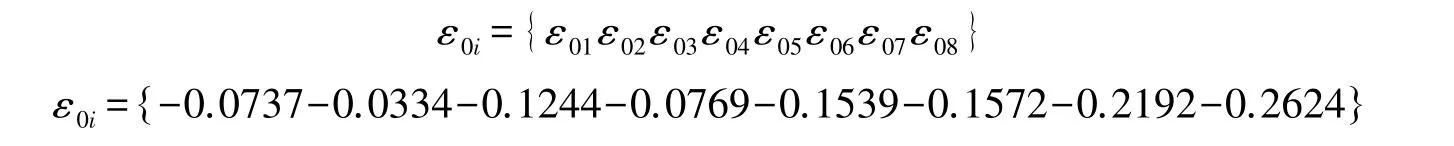
排序得到:ε02＞ε01＞ε04＞ε03＞ε05＞ε06＞ε07＞ε08。

由以上结果可得，B8对地方政府债务的影响最小，属于冗余指标，剔除B8“税收收入占比”指标，选择剩余8个指标B1、B2、B3、B4、B5、B6、B7、B9作为预警指标体系。

3.2 地方债务风险指数的测算与评估

BP神经网络是一个包含输入层、隐含层和输出层的完整系统。输出层为已知量，是地方政府债务风险综合评价值。本文运用层次分析法(Analytic Hierarchy Process)测算2015年重庆市38个区县样本数据的债务风险综合评价值，以此作为BP神经网络输出值的参照指标。

3.2.1 关键预警指标的统一量纲化处理

为了能准确比较各债务风险综合评价值，鉴于各预警指标的性质和衡量标准不同，需要对样本数据进行统一量纲化处理。本文采用区间映射法，对每项指标设定相对应的风险指数区间，将样本数据转化为可操作性的指数值。即从风险较小的“绿色可控区”“橙色预警区”到风险较大的“红色风险区”指数区间依次为[0，1]、(1，2]、(2，∞)。

假设Ri为剩余8项指标Bi经处理后的指数值，则Ri可通过公式(1)确定:

其中，Bi为样本值，Eu为该样本值所处风险指数区间的上限，Ed为该样本值所处风险指数区间的下限。

若样本值所处风险指数区间无上限，则采用公式(2)计算Ri:

其中，Eu－1为相邻风险指数区间的上限，Ed－1为相邻风险指数区间的下限。

3.2.2 关键预警指标权重的确定

本文运用AHP法测算出各预警指标的主观权重。最终的权重采用主客观组合赋权的思路确定。本文运用yaahp层次分析法软件辅助计算得出权重。首先对8个关键指标建立层次结构模型，模型的层次结构图如图1所示。采用专家打分法，对准则层及方案层指标运用1－9比率标度法进行两两比较，构造判断矩阵，并通过一致性检验，确保测算权重的合理性，从而得出关键指标的主观权重(如表4)。

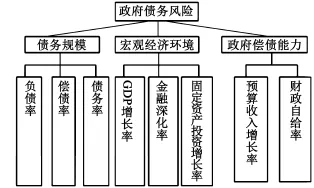
图1 层次结构图

表4 基于AHP法关键预警指标确定政府债务风险主观权重

3.2.3 样本数据的债务风险综合评价值的测算

样本数据的综合评价结果可由公式(3)得出:

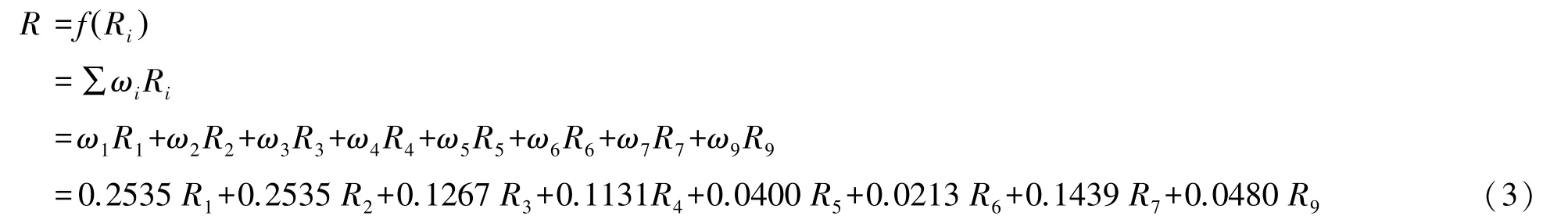
公式(3)中，R为债务风险指数综合评价值，Ri为关键指标经处理后的指数值，ωi为各项关键指标的主观权重，R值表示风险状态为“绿色可控区”、“橙色预警区”和 “红色风险区”的取值区间依次为R∈[0，1]、R∈(1，2]、R∈(2，∞)，见表5。

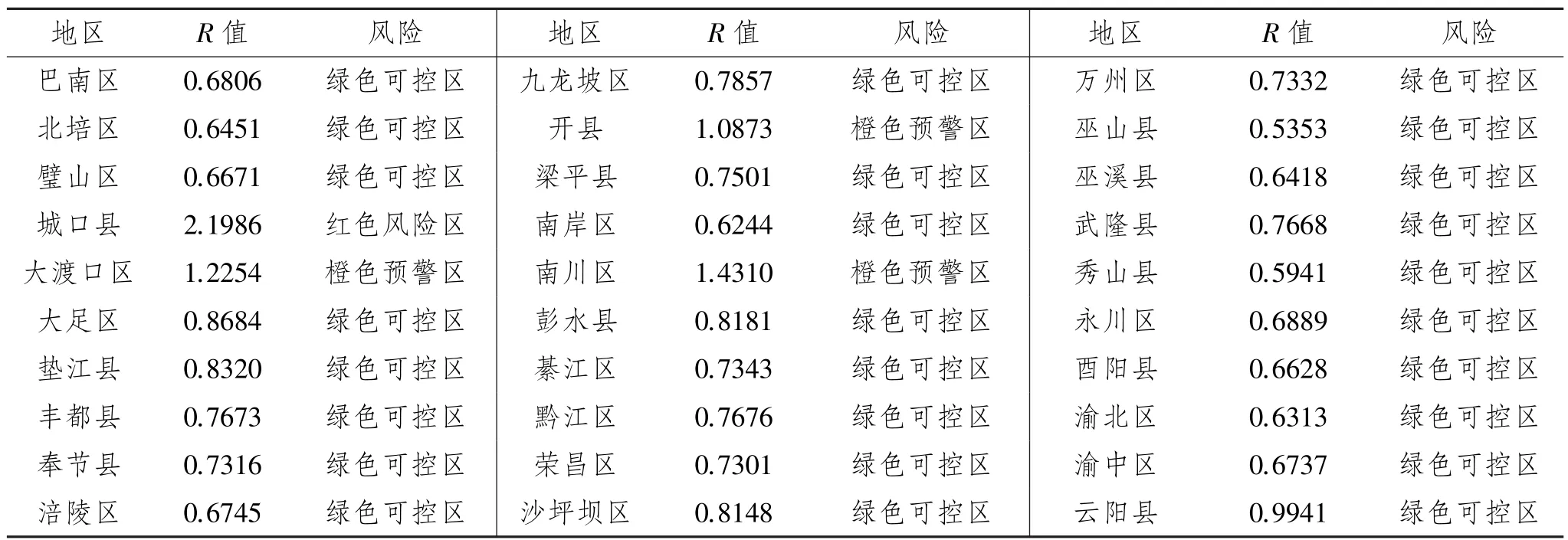
表5 38个样本的债务风险指数和等级

续表5

3.3 运用BP神经网络训练和检验

BP神经网络的输入层节点是经灰色关联理论约简后的剩余8项关键指标，输出层节点是地方政府债务综合评价值即R值。隐含层节点个数与输入层节点和输出层节点个数有关，往往需要通过多次试验来确定。本文借助AMPL软件编程求得隐含层个数。经试验，隐含层节点数为2时，匹配度为0.001 6，具有较高的准确率。基于本文38个样本数据，最终确定输入层节点数为8；隐含层节点数为2；输出层节点数为1。

本文从38个样本数据中随机抽取5个样本作为检验样本，抽取的样本地区分别为丰都县、奉节县、九龙坡区、梁平县、綦江区。剩余的33个样本数据作为训练样本。运用 Matlab8.1软件中的神经网络工具箱(nntraintool)对设计好的GM－BP神经网络进行检验，对GM－BP神经网络的函数和参数设定如下:

(1)数据归一化处理。由于各指标的衡量标准及性质不同，样本数据之间存在计量单位的差别，为避免因为数据数量级差别放大网络预测误差，因此对数据进行归一化处理，将所有的数据都转化为[－1，1]之间的数值。本文采用最大最小法，其函数形式为:xk＝(xk－xmin)/(xmax－xmin)。

(2)传递函数和训练函数。由于本文的神经网络结构为8－2－1，因此选取tansig函数和purelin函数分别作为隐含层和输出层神经元的传递函数。训练函数采用trainlm函数，该函数收敛速度较快，能够提高神经网络的泛化能力。

(3)目标误差、最大训练次数和学习率。设定神经网络的目标误差为0.001，最大训练迭代次数为500，学习率为0.01。

借助AMPL软件，将GM－BP神经网络根据既定函数和参数训练38个样本，结果表明，训练得出的期望输出与实际输出相差不大，二者的均方误差(mean square error)仅为0.0016，训练效果较好，预警准确性较高。由8个关键指标构建的GM－BP神经网络的迭代次数为116次。同时，为了验证本文构建的GM－BP神经网络的优越性与实用性，将未经灰色关联方法约简的9个指标作为输入层节点，输出层节点不变，依旧为地方债务风险综合评价值R。运用AMPL软件对未经约简的BP神经网络按照上述相同的函数、参数进行训练，求得结果表明，未经约简的BP神经网络迭代次数需要335次，迭代次数明显增多，增加了训练时间，期望输出与实际输出的误差值低于GM－BP神经网络。

将随机选取的丰都县、奉节县、九龙坡区、梁平县和綦江区5个样本的8项关键指标输入训练好的GMBP神经网络中，得到如表6所示的样本实际输出值。同时将5个样本的实际输出与期望输出值对比，求得检验效果([1－(期望输出－实际输出)/期望输出]×100%)均在97%以上，抽取的五个样本中四个样本达到了100%匹配，预警仿真效果理想。从而说明本文设计的GM－BP神经网络预警系统是有效的，能够发挥风险预警的功能。与此同时，将5个检验样本输入未经约简的地方政府债务风险预警系统中，得到表7所示的样本实际输出。未经约简的神经网络检验效果均低于97%，检验效果不如GM－BP神经网络。

表6 GM－BP神经网络检验结果

表7 未经约简的BP神经网络检验结果

从神经网络的训练方面看，未经约简的神经网络需要经过335次的迭代才能达到网络收敛的稳定性标准，而GM－BP神经网络只需要116次迭代就能达标。灰色关联方法显著提高了神经网络的训练速度，缩短了训练时间。从神经网络的检验方面看，GM－BP神经网络的准确性更高，实际输出与期望输出更接近，仿真效果更好。故本文构建的GM－BP神经网络准确简洁，不但节省了训练时间，提高了神经网络的学习能力，而且约简了预警系统的指标，提高了预警系统的准确性。

4 结论及政策建议

4.1 结 论

本文将灰色关联理论与BP神经网络相结合，构建出基于GM－BP神经网络的地方政府债务风险预警系统。选取重庆市2015年38个区县的债务数据作为样本数据，对风险预警系统进行了实证分析，结论如下:

第一，本文运用灰色关联方法，对最初构建的地方债务风险预警指标体系的三大子系统中9个指标进行关联度排序，删除关联度最小的冗余指标，最终选取了负债率、偿债率、债务率、GDP增长率、金融深化率、财政自给率、固定资产投资增长率、预算收入增长率8个关键指标，作为债务风险预警系统的指标体系。运用AHP法测算出2015年重庆市38个区县的债务风险指数相应的风险评价等级。2015年重庆市33个区县债务风险处于绿色可控区，4个区县(大渡口区、开县、南川区、潼南区)处于橙色预警区，仅有城口县债务风险处于红色风险区。以上结果表明2015年重庆市各区县风险总体可控，但个别区县的债务风险较高，尤其是城口县债务风险已达到红色风险区，应引起重庆市各区县政府的重视。

第二，运用灰色关联方法约简债务风险指标，将剩余的8项关键指标作为BP神经网络的输入值，给定的地方政府债务风险综合评价值R作为输出值，对重庆市38个区县的样本数据和随机选取的5个区县的数据对GM－BP神经网络进行训练和检验。检验结果表明，GM－BP神经网络的检验效果比未经约简的效果要好，迭代次数更少，训练时间更短，预警准确性更高。

第三，该预警系统具有普适性。在今后我国的地方政府债务风险预警过程中，只要获得这些地区的相关预警指标原始数据，并且根据债务数据所处的地区相应的调整指标区间，将原始数据输入调整好的GM－BP神经网络债务风险预警系统中进行评估，便可得到所需的债务综合评价值R以及相对应的预警区间。这样做能够避免因主观随意性对债务风险进行误判，使评估更加客观、科学，从而方便政府及时准确地对债务风险做出预测。

当然，本文所构建的基于GM－BP神经网络的地方政府债务风险预警系统是参考了以往成熟的理论研究成果，并结合实际所选样本数据设计得出的，可以说其是一个动态性的预警过程，所得出的债务风险结果也仅是经过科学预警得出的参考值，因此需要我们今后进行定期研究并对预警系统进行修正。

4.2 政策建议

结合基于GM－BP神经网络的地方政府债务风险预警模型结果以及我国地方政府债务管理实践，为更好地预防和规避我国地方政府债务风险，我们认为还应注意以下几个方面:

首先，厘清各种性质的地方性债务风险，建立更具针对性的、细化的预警指标体系。区分地方政府存在的直接、或有债务和显性、隐性债务，根据不同地区的整体经济情况与债务状况，建立能够反映本地区实际情况的预警指标体系，从而实现地方政府债务风险的精准预警。

其次，开源节流，加快培育地方政府主体税种，优化地方政府支出结构。除构建地方政府债务风险预警系统外，要想降低财政风险，从根本上来说，还得依靠增收节支。营改增后我国地方主体税种的缺失将增大地方政府债务风险，应加快选择培育适合成为地方税收主体来源的税种。同时还应加强对预算的管理和监管，建立健全全面规范、公开透明的预算制度以及债务信息披露体系，规范地方政府支出行为。

最后，建立与地方政府债务风险预警系统相配套的应急处置预案。定期评估各地区政府性债务风险情况，及时实施风险评估和预警。同时建立健全地方政府性债务风险应急处置工作机制，成立应急组织机构，实现快速响应、分类施策、各司其职、协同联动、稳妥处置，做到预警系统和应急处置预案的衔接和协调。并在债务风险事件应急处置结束后，对债务风险事件应急处置情况进行评估，并根据评估结果，及时总结经验教训，改进完善债务风险预警系统和应急处置预案。

[1]POLACKOVA H.Government Contingent Liability:A Hidden Fiscal Risk[M].Quarterly Magazine of the IMF，1998.

[2]BURNSIDE C.On Contingent Liabilities and the Likelihood of Fiscal Crises[M].Comparative Economic Studies，2002.

[3]MARTNER R，TROMBEN V.Public Debt Indicators In American Countries:Snowball Effect[J].Currency Mismatch and The O-riginal Sin Social Science Research Network，2004(4):56－90.

[4]巴曙松.地方债务问题应当如何化解[J].西南金融，2011(10):4－6.

[5]陈睿.我国地方债务危机的成因、影响及对策[J].商丘师范学院学报，2011(10):97－100.

[6]孙浩颉.关于地方政府性债务风险分析及管理建议[J].经营管理，2015(1):80.

[7]CHARLE S.Measuring and Forecasting Debt Capacity State of Oregon Experience[J].Government Finance Review，2008(12):44－74.

[8]MA J.Monitoring Fiscal Risks of Subnational Governments:Selected Country Experiences[M].Oxford:Oxford University Press，2003.

[9]刘尚希，赵全厚.政府债务:风险状况的初步分析[J].管理世界，2002(5):22－32.

[10]裴育，欧阳华生.我国地方政府债务风险预警理论分析[J].中国软科学，2007(3):110－114.

[11]洪源，刘兴琳.地方政府债务风险非线性仿真预警系统的构建——基于粗糙集－BP神经网络方法集成的研究[J].山西财经大学学报，2012(3):1－10.

[12]王振宇，连家明，郭艳娇，等.我国地方政府性债务风险识别和预警体系研究——基于辽宁的样本数据[J].财贸经济，2013 (7):17－28.

[13]朱文蔚，陈勇.我国地方政府性债务风险评估及预警研究[J].亚太经济，2015(1):31－36.

[14]邵伟钰.地方政府债务风险预警体系研究[D].江苏:苏州大学，2008.

[15]刘骅，卢亚娟.地方政府融资平台债务风险预警模型与实证研究[J].经济学动态，2014(8):63－69.

[16]曹明霞.灰色关联度模型正负性问题的研究及其改进[J].系统工程与电子技术，2008(6):1086－1088.

[17]温正.精通MATLAB智能算法[M].北京:清华大学出版社，2015.

[18]余胜威.MATLAB优化算法案例分析与应用[M].北京:清华大学出版社，2014.

Local Government Debt Risk Warning System Based on GM－BP Neural Network——A Case Study of 2015 Sample Data from 38 Chongqing Districts and Counties

MA Entao，LV Hanping
(School of Finance and Taxation，Shandong University of Finance and Economics，Jinan250014，China)

With the 2015 debt data from 38 Chongqing districts and counties as sample and via the nonlinear processing advantages of grey correlation method and BP neural network，this paper constructs a GM－BP neural network－based local government debt risk warning system and empirically analyzes the debt risks of all Chongqing districts and counties by adopting this warning system.The results show that in 2015 the debt risks of 38 Chongqing districts and counties remain in the Green Zone with 4 districts and counties(Dadukou District，Kaixian County，Nanchuan District and Tongnan District)in the orange warning area and 1 county(Chengkou County)in the red risk area while Chongqing local government debt risks are overall controllable，and that compared with the unreduced BP neural network warning system，the GM－BP neural network debt risk warning system needs a shorter training time，has higher early warning accuracy，and presents a certain degree of universality if fine－tuned according to the actual situation of early warning areas.

grey correlation method；BP neural network；local government debt risk；warning system

F810.7

:A

:2095－929X(2017)02－0096－11

(责任编辑 时明芝)

2016－11－02

国家社会科学基金项目“我国地方政府融资平台债务控制及其风险防范研究”(13BJY164)；山东省自然基金重点项目“山东省政府性债务控制及风险预警研究”(ZR2015GZ001)；济南市社科规划基金重点项目“济南市政府与社会资本合作中的问题与对策研究”(JNSK16B04)。

马恩涛，男，山东德州人，经济学博士，山东财经大学财政税务学院教授，研究方向:政府债务问题研究；吕函枰，女，山东烟台人，山东财经大学财政税务学院硕士生，研究方向:政府债务问题研究，Email:lhping6688@163.com。