谈概率统计教学

吴艳华

《统计与概率》是初中数学四个学习领域之一，但由于这部分内容较少，在中考中所占的比分较少，要求也不高，所以在实际教学中，没有得到充分的重视。实际教学中，教师往往让学生背公式，熟记计算，却没有真正理解教材，按照学生的认知规律安排教材。事实上，对概率统计的接受需要经历收集数据，检验并调整自己的直觉等过程，这需要延续较长的时间，才能形成较为完整的概率统计意识。那么，教师如何讲好统计与概率呢？笔者以一节《方差》为例，谈一谈对《统计与概率》教学的认识。

教材、学情分析和教学目标

方差是苏科版初中数学九年级（上册）第三章第四节的内容，此前学生已经学习过平均数、中位数和众数，这三个数据是刻画数据集中趋势的主要统计量。数据的集中趋势仅仅是数据分布的一个特征，反映的是一组数据向其中心值聚集的程度。本节课就是要研究数据之间的差异，考查数据的波动情况，即数据的离散程度，这是对数据分析的另一重要指标。这是对前面八年级所学有关统计内容的延续。

知识与技能：掌握极差、方差的概念，会计算极差、方差，理解它们的统计意义；了解极差、方差是刻画数据离散程度的统计量，并在具体情境中加以应用。

过程与方法：通过一系列富有启发性、层层深入的问题，经历对数据的分析，能用样本方差估计总体方差。

情感态度与价值观：培养学生认真、耐心、细致的学习态度和学习习惯；培养学生探求知识的勇气，体会教学活动的探索性和创造性。

案例解析

教学设计 10月中旬，我校将要举行校运动会了，同学们都踊跃报名。但由于每个项目都有人数限制。为了我们班级能取得更好的成绩，现在要从报名参加100米跑步比赛的两位同学中选拔一人参加比赛。老师特意要来了他们两个人平时的训练成绩，请看下表（单位：秒）。你会选谁？（设计意图：利用学生熟悉的情境体现数学来源于生活，又服务于生活。）

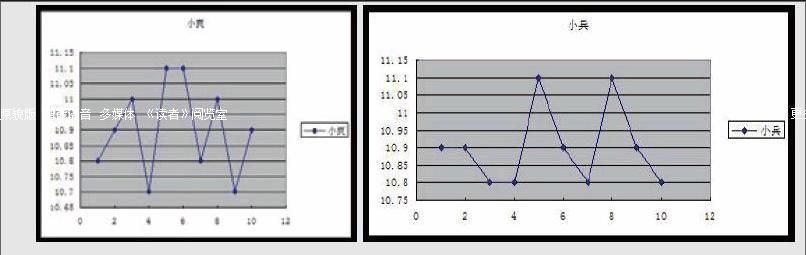
探究活动 课堂上，有学生说：分别计算两个人的平均成绩，谁的平均成绩好，就选谁。教师肯定地说：好主意！分小组计算两位选手的百米赛跑平均成绩，通过计算发现两位选手的百米赛跑平均成绩均为10.9秒。平均成绩相同，两位选手的水平就一模一样吗？观察这些数据，我们还可以从哪些方面来考量这两位选手的成绩，比如成绩的稳定性、最好成绩等。最后，学生小组讨论，得出两组数据特点：小爽的成绩波动幅度大，小兵的波动幅度小。

教师问：波动幅度大小是怎么看的？有学生回答：小爽的最好成绩是10.7秒，最慢的成绩是11.1秒，相差0.4秒。小兵的最好成绩是10.8秒，最慢成绩是11.1秒，相差0.3秒。

教师总结：我们把一组数据的最大值和最小值的差叫做极差。极差反映了一组数据的变化范围，在一定程度上描述了这组数据的离散程度。（板书）在有些情况下，我们只需要知道极差就够了，如天气预报只报最高气温和最低气温，因为对于一般人来说，只需要知道这两个极端值，气温的变化范围就可以了。但是极差只是利用了一组数据两端的信息，不能反映出中间数据的分散情况，那么怎样才能衡量整个一组数据的波动大小呢？老师提供一种方案供大家参考：将两位选手的成績以点的形状标注在平面直角坐标系里，然后用折线连接，确定平均数为中心线，从而观察波动情况。散点（如下图）可以比较明显的看到有多少数据在波动，数据偏离中心的幅度有多少。但这种绘制图像的方法仍然是定性的综合印象。怎样才能定量的计算整个数据的波动大小呢？（设计意图：为了直观地看出两组数据的离散程度（波动情况），绘制了两个“散点图”使学生对数据偏离平均数的情况有一个直观的认识，为引入“方差”的概念做好铺垫。）

学生：计算偏差，每个数据与平均数的差。

老师：如何累计偏差？

学生1：计算偏差的和。（学生先想到求代数和，但很快能自己发现问题）

学生2：不能求和，正负偏差会相互抵消的。小爽的偏差和就为0，而小兵为-0.1，和刚才的观察结果不符合。

老师：那如何使正负偏差不相互抵消呢？

学生：小组讨论后得出两种方法：①给每个偏差加上绝对值后再相加；②给每个偏差平方后再相加。

老师：我们以一组数据（下图）为例来分析一下该选用哪种方案更好些。

（设计意图：由学生提出方案后，学生会积极运算，想快速得出结果，验证自己的方案）

学生分组计算，第一种方案各数据与平均数的偏差的绝对值的和均为20，但按照第二种方案求各组数据的偏差平方和，甲组为164，乙组为104.所以我们应该选用第二种方案，给每个偏差平方后再相加。在很多问题里，含有绝对值的式子不便于运算，而且在衡量一组数据的离散程度（波动大小）的“功能”上，将各偏差平方更强些。

老师：数据的偏差的平方和与什么还有关系？请分别计算下列两组数据偏差的平方和。

让学生自己动手计算，求平均数时激发学生用简便方法计算，找一位学生到黑板上板演。

老师：观察与计算为什么有矛盾？

学生：因为两组数据的个数不一样。

老师：那么在数据个数不一样的情况下，如何合理计算偏差呢？

学生：计算偏差平方的平均数。

老师：请同学们分别计算上述两组数据偏差平方的平均数。

学生：计算两组数据偏差平方的平均数。

老师：现在观察与计算还矛盾吗？我们把一组数据偏差平方的平均数叫做这组数据的“方差”。（板书方差定义）

教师总结：一组数据的方差越大，说明这组数据的离散程度越大，也就是数据的波动越大，越不稳定。方差越小，说明这组数据的离散程度越小，数据的波动越小，越稳定。请同学们总结计算方差的步骤。

学生小组讨论后给出下列步骤：①计算数据的平均数；②计算偏差；③计算偏差的平方和；④除以数据的个数。

老师：学完方差的概念后，请同学们帮助老师一起来选拔一位同学参加校运动会的百米赛跑。

学生：通过计算，小爽的方差为0.018，小兵的为0.007。小兵的方差小，成绩稳定，选小兵。

（设计意图：使学生深刻体会到数学来源于生活。又反过来服务于生活，不仅使学生对学习数学产生浓厚兴趣，而且培养了学生应用数学的意识。）

课堂小结 本节课你学到了什么？在利用本课知识时，你想提醒同学们注意哪些方面？你还有什么收获？（设计意图：通过学生的总结，不仅可以进一步巩固所学知识，还可以培养学生以积极的情感态度，探索问题，进而体会数学应用的科学价值。）

课后反思

在活动过程中，教师要改变常规的教学法，采用实践教学活动来引领学生学习，教师作为活动的引导者和合作者，让学生通过交流合作、主动探究，在收集和处理数据的实践中领悟、在概念讲解中要多举例子，让抽象的概念和生活实际联系起来，这样便于学生理解。同时，教师还要注意培养学生正确的学习方法，提倡合作、探究、实践、创新的学习精神，充分体现学生在学习中的主体地位。只有这样，才能不断培养学生的数据分析观念。

（作者单位：江苏省苏州工业园区娄葑学校）