基于遗传算法的带筋壁板条带激光喷丸成形工艺优化研究

杨荣雪，胡 蓝，胡永祥，姚振强

（1.上海交通大学机械与动力工程学院，上海200240；2.上海交通大学机械系统与振动国家重点实验室，上海200240；3.上海航天设备制造总厂，上海200245）

基于遗传算法的带筋壁板条带激光喷丸成形工艺优化研究

杨荣雪1，2，胡 蓝3，胡永祥1，2，姚振强1，2

（1.上海交通大学机械与动力工程学院，上海200240；2.上海交通大学机械系统与振动国家重点实验室，上海200240；3.上海航天设备制造总厂，上海200245）

为实现带筋壁板条带激光喷丸成形目标曲面，对基于遗传算法的激光喷丸条带分布工艺优化方法进行了研究。建立了固有应变的带筋整体壁板有限元模型，将条带的优化转换为仿真所获曲面与理想目标曲面偏差最小问题，用遗传算法对喷丸条带宽度与间隔进行优化，给出了优化流程，以及遗传算法操作参数的设置。以单筋壁板成形圆柱面为实例，实现了其条带分布优化，获得成形曲面曲率半径与目标圆柱半径偏差为1%，对应节点最大距离0.003 3mm。优化结果表明：遗传算法可较好地适应本优化问题中目标函数难求导的状况，同时执行多方向搜索提高了优化效率。

带筋壁板；激光喷丸成形；条带喷丸；固有应变；参数优化；有限元建模；遗传算法；曲面

0 引言

整体壁板作为一种薄壁加筋结构，其蒙皮、加强凸台、筋条等结构要素间无任何机械连接，具有质量轻、承载效率高的优点，正越来越多地用于航空航天设计制造领域［1－2］。条带激光喷丸成形具有高应变率效应，能产生幅度和深度更大的残余压应力场，故可实现更大曲率曲面的成形［3］。采用激光作为能量源，可根据成形件的要求，有目的选择部分条带区域进行激光喷丸，在带筋壁板成形方面具有独特优势［4］。分区域的条带喷丸较早就用于传统机械喷丸成形机翼壁板。HARBURN，MILLE最早采用分区喷丸的方式成形波音飞机壁板，而美国Pangborn公司在生产单曲率蒙皮时率先采用了条带喷丸方法［5］。喷丸成形中，板件的弯曲曲率取决于激光冲击形成的压力层深度及压力层中残余压应力的大小。因此，用相同激光脉冲进行条带喷丸成形时，影响板件成形效果的主要工艺参数是激光扫描区域，即条带宽度和间隔宽度。文献［6］研究了条带喷丸中间隔对最终成形的影响；文献［7］针对气动条带喷丸成形大型复杂型面提出了整体分条、条带分区的方法；文献［8］研究了平板成形曲率与喷丸条带间距的关系。在应用中，条带激光喷丸中激光扫描区域的确定常需要进行大量试验，或是按基于试验结果的数值方法设定，工艺参数的确定常需耗费大量的时间和资源。为此，本文提出用遗传算法对激光喷丸条带分布进行参数优化的方法：由带筋壁板激光喷丸有限元模型建立条带分布与宏观成形效果间的关系，用遗传算法优化条带宽度和间隔宽度，并以单筋壁板成形圆柱面验证该优化方法的可行性。

1 条带激光喷丸成形工艺

激光喷丸成形是用高功率短脉冲激光按一定的路径和速度辐照在有吸收层和约束层的材料表面，通过激光诱导冲击效应在材料内部产生非均匀分布残余应力，实现板材成形的工艺。作为一种无模成形工艺，通过控制激光参数、扫描路径等工艺参数可获得理想的弯曲变形。条带激光喷丸作为一种选择性的喷丸方式，仅对壁板部分区域沿规划好的路径进行激光冲击，其喷丸痕迹为条带状，如图1所示。整个壁板表面划分为喷丸区域和间隔区域，且条带路径即为激光脉冲扫描方向。壁板表面条带分布将会影响激光喷丸成形工件最终形状，即该工艺中条带分布是控制工件成形的重要工艺参数。与无差别全面积激光喷丸相比，条带激光喷丸路径规划更灵活，可实现复杂路线的激光扫描，利于成形复杂外形。

2 筋条壁板固有应变模型

对带筋整体壁板激光喷丸成形工艺的模拟是基于固有应变理论的分层壳单元建模［9］。如图2（a）所示，先沿壁板厚度方向建立分层壳单元，再设置材料属性中的线膨胀系数在每层施加实验标定的固有应变，使各层的固有应变沿厚度（深度）方向满足

表征的高斯函数分布［10］。此处：ε＊为固有应变；a，b，c为由光斑X、Y向搭接率决定的系数；x为薄板厚度方向位置坐标；h为薄板厚度。在壁板模型中激光冲击的区域根据上述方法设置分层壳单元即可在特定区域引入固有应变，从而模拟仅对壁沿规划好的区域进行激光冲击，条带喷丸如图2（b）所示。

基于固有应变方法，壁板的非筋平板部分采用上述平板分层壳单元建模方法。建立筋条部分模型，首先需满足工程准确性和精度，尽可能如实反映结构特征和工艺过程，其次需满足经济的建模和计算效率。因此，选择梁单元模拟壁板的加强筋部分，设置梁单元与壳单元有共同节点会使建模和计算较方便。此时壳单元节点位于壳的中性面上，梁单元节点位于梁横截面的某处，两节点重合，如图3所示。通过梁截面偏移的设置，可保证壁板整体刚度符合实际，筋条部分变形则全部由沿梁长度方向的公共节点的位置函数决定。

3 带筋壁板条带激光喷丸工艺参数优化设计

3.1 优化问题描述

条带激光喷丸的条带分布对双向成形曲率差异有显著影响，工件经过条带激光喷丸后最终的弯曲变形是喷丸条带区弯曲变形，间隔区域限制弯曲变形相互牵制作用的结果。故条带分布是控制工件最终成形的重要参数，对该工艺的工艺参数优化来说就是对条带分布的优化。

利用上述基于固有应变的带筋壁板有限元仿真模型，通过数值模拟方法，可获得不同条带分布下筋条壁板的成形结果，并据此进行条带分布的优化设计。条带分布的优化，是以仿真所获得曲面与理想目标曲面偏差最小为目标，对喷丸条带宽度SW和条带间隔宽度IW进行优化。如图1所示，对尺寸确定的工件，描述条带分布变量间的关系满足

式中：SN为喷丸条带数量；IN为条带间隔数量；xlength为喷丸条带分布方向上工件边长。

3.2 遗传算法优化实现及求解

给定理想目标形状的条带分布优化问题有以下特征：以仿真曲面与理想曲面偏差最小为单目标；目标函数值通过有限元仿真数值模拟过程获得，故没有明确的函数表达式；优化参数为SW，IW，即为多设计优化变量。这些特征对本问题的优化算法提出了一定要求，故选择的优化算法应兼顾效率和精度。与基于梯度的优化算法相比，选择遗传算法作为优化算法，可适应本问题目标函数难以求导的问题，并通过执行多方向搜索提高优化效率。

遗传算法在优化设计中的应用是基于达尔文的适者生存，优胜劣汰的自然选择机制，模拟生物的进化过程演化而来的，是一种全局性的概率搜索算法［11］。其优化机理是：从随机生成的初始群体出发，采用基于适应度函数的选择策略选择优良个体作为父代；通过父代个体的复制、交叉和变异繁衍进化的子代种群；当优化过程结束时，具有最大适应度值的个体对应的设计变量值即为优化问题的最优解［12］。遗传算法用于优化条带激光喷丸成形工艺的流程如图4所示。

算法中的适应度函数和约束函数需具体确定。对给定的目标曲面，以仿真曲面各节点位置坐标Zs与理想的目标圆柱面各节点位置坐标Zd偏差最小为目标，即为遗传算法中的适应度函数。仿真曲面成形曲率半径Rs与理想曲面曲率半径Rd的偏差需保持在一定范围内，即为遗传算法中约束函数。取设计变量X中的条带宽度xs、间隔宽度xi为整数，令f为目标函数即适应度函数，g为约束函数，K为偏差系数，则条带激光喷丸条带分布优化问题的数学模型为

用遗传算法优化时，参数设置见表1。用适应度比例法选择个体。假设群体数量为MPOP，个体i的适应度为fi，则该个体被选择的概率Pi＝。因此，个体的适应度愈大，其被选择的概率愈高，反之亦然。

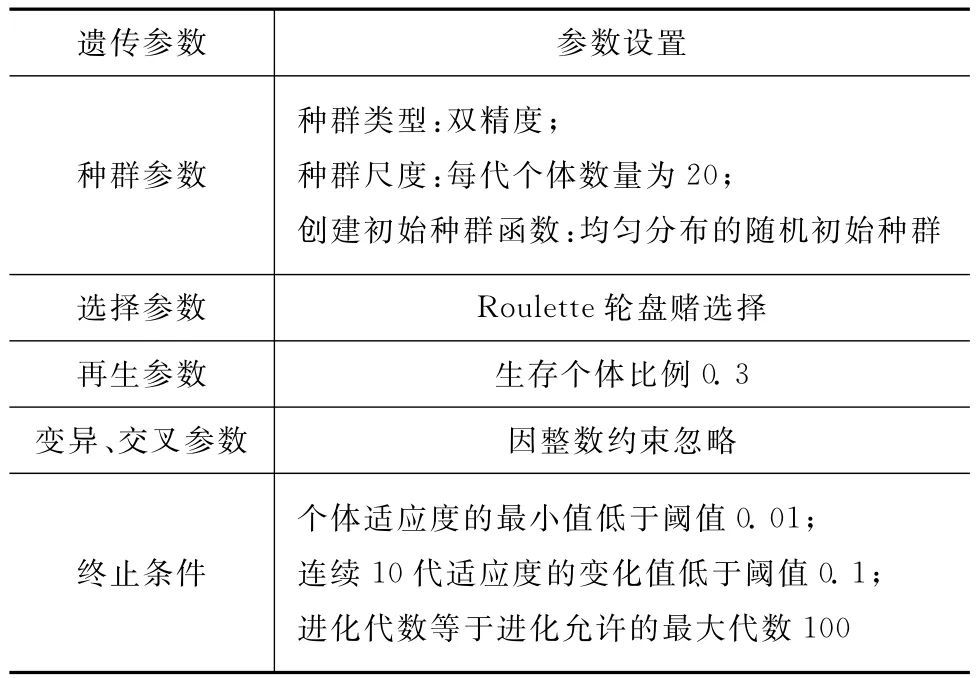
表1 遗传算法操作参数设置Tab.1 Parameters of genetic algorithm

3.3 优化算例

如图5（a）所示，带筋壁板尺寸为长100mm×宽100mm×高2mm，筋条为矩形截面，截面尺寸为高8mm×宽2mm，筋条的分布方向平行于Y向，等间距分布，筋条间距为12mm，喷丸条带和间隔交替分布。材料为2024－T3铝合金，条带区域的固有应变为X、Y向的激光搭接率均为50%时的仿真数值，间隔区域和筋条部分的固有应变为零。成形目标曲面为半径Rd＝400mm圆柱曲面，如图5（b）所示。遗传算法优化过程如图6所示。优化进行到42代左右终止，所得SW＝6mm，SN＝6，IW＝12mm，获得成形曲面形状最接近目标曲面，优化结果有限元模型如图7（b）所示。优化后，优化种群中最优个体与目标曲面对应节点间最大距离0.003 3mm，且单筋壁板在垂直于筋条方向成形曲率Rs＝396mm，与Rd＝400mm偏差4mm。

由该算例可认为：针对目标曲面，用遗传算法对带筋壁板条带激光喷丸成形条带分布的优化是有效的，优化后的曲面如图7所示。需注意的是：优化曲面与目标曲面在垂直于筋条方向的弯曲变形基本一致，成形轮廓线接近圆，但优化曲面在筋条方向不完全是直线，成形曲面并非为理想圆柱面。这是由激光喷丸成形特点形成的，它必然会在沿平面的两个方向上引入应变。故此成形差异不能完全克服，但可通过合理选择工艺参数和喷丸路径予以抑制。

4 结束语

条带几何分布是控制壁板条带激光喷丸成形形状的关键工艺参数。本文结合激光喷丸成形带筋壁板有限元模型，提出了一种基于遗传算法的条带激光喷丸工艺参数优化方法。以单筋壁板成形圆柱面为实例，实现了其条带分布优化，获得成形曲面曲率半径与目标圆柱半径偏差为1%，表明了此优化模型的有效性。不同规格带筋壁板可用此优化方法以成形所需目标形状。由于目标函数值通过有限元仿真获得，将遗传算法应用在本优化问题中，其作为全局性概率搜索方法寻优不依赖于函数梯度，故较好地适应了目标函数难以求导的特性，且优化参数为一组关联的条带宽度和间隔宽度，遗传算法能对两个设计变量同时进行多方向寻优搜索以提高优化效率。若希望将本模型用于不同目标成形曲面，则适应度函数需作调整，因此可设定更简洁、通用的方法标定适应度值，对现有优化模型进行改进。

［1］ 王秀凤，郭晓丽，陈光南，等.整体壁板成形评述［J］.现代制造技术与装备，2008（3）：1－4.

［2］ 曾元松，黄遐.大型整体壁板成形技术［J］.航空学报，2008，29（3）：721－727.

［3］ 叶天麟，周天孝.航空结构有限元分析指南［M］.北京：航空工业出版社，1996.

［4］ 张兴权，张永康，周建忠，等.激光窄条喷丸成形的实验研究［J］.中国激光，2007，34（10）：1446－1450.

［5］ 杨永红，吴建军，乔明杰.现代飞机机翼壁板数字化喷丸成形技术［M］.西安：西北工业大学出版社，2012.

［6］ 尚建勤，徐天浩.喷丸条带间隔对喷丸成形影响的试验研究［J］.航空制造技术，2001（3）：44－46.

［7］ 杨永红，张贤杰，王俊彪，等.气动条带式喷丸成形技术［J］.航空制造技术，2008（2）：91－93.

［8］ 张兴权，张永康，周建忠，等.基于激光喷丸的板料成形试验研究［J］.塑性工程学报，2007，14（5）：62－66.

［9］ HU Y，GRANDHI R V.Efficient numerical prediction of residual stress and deformation for large－scale laser shock processing using the eigenstrain methodology［J］.Surface ＆Coatings Technology，2012，206（15）：3374－3385.

［10］ HUH M Y，CHO S Y，ENGLER O.Randomization of the annealing texture in aluminum 5182sheet by cross－rolling［J］.Materials Science and Engineering A，2001，315（1－2）：35－46.

［11］ JH H.Adaptation in natural and artificial systems［M］.Cambridge：MIT Press，1975.

［12］ 边霞，米良.遗传算法理论及其应用研究进展［J］.计算机应用研究，2010，27（7）：2425－2429.

Optimization of Strip Laser Peen Forming by Genetic Algorithm for Stiffener Integral Panels

YANG Rong－xue1，2，HU Lan3，HU Yong－xiang1，2，YAO Zhen－qiang1，2
（1.School of Mechanical Engineering，Shanghai Jiao Tong University，Shanghai，200240，China；2.State Key Laboratory of Mechanical System and Vibration，Shanghai Jiao Tong University，Shanghai，200240，China；3.Shanghai Aerospace Equipments Manufacturer，Shanghai，200245，China）

To obtain the specified surface，the layout optimization of the peening strip in strip laser peen forming based on genetic algorithm was discussed.The finite element model of stiffener integral panel with inherent stain was established.The layout optimization was transferred to the problem of minimum deviation between the curved surface obtained by simulation and the ideal curved surface.The width and distance of peening strip were optimized by genetic algorithm.The optimization flowchart was given.And the parameters were set for genetic algorithm operation.A unidirectional stiffener integral panel forming cylindrical shape was taken as an example and its optimal layout was realized by this approach.It was 1%deviation of curvature radius between simulated curve and target cylinder and the maximum distance between the corresponding nodes was 0.003 3mm.It demonstrated that genetic algorithm was effective to solve the difficulty with the derivation problem of objective function，and improved the optimizing efficiency by searching candidate solutions multi－orientatedly.

stiffener integral panel；laser peen forming；strip peening；inherent stain；parameter optimization； finite element modeling；genetic algorithm；curved surface

TN249：TG668

A

10.19328／j.cnki.1006－1630.2017.01.005

1006－1630（2017）01－0032－05

2016－09－18；

2016－11－21

国家自然科学基金面上项目资助（51375305）；航天先进技术联合研究中心技术创新项目资助（USCAST2015－26）

杨荣雪（1992—），女，硕士生，主要从事激光加工研究。