R语言在统计分析中的使用技巧

刘二钢+马建强

摘要：R语言在统计分析中的应用已经越来越广泛。文章通过一些实例，简要地介绍了R语言在统计分析中的一些技巧和应用，希望能够为广大读者学习R语言提供一些启迪和借鉴作用。

关键词：R语言；统计分析；统计函数；检验

中图分类号：TP312 文献标识码：A 文章编号：1009-3044（2017）01-0251-03

Abstract： The R language in the application of statistical analysis has been more and more widely.This paper introduces the R language techniques and applications in statistical analysis through some examples， and wants to be able to provide some enlightenment and reference for the readers to study the R language.

Key words： R language； statistical analysis； statistical function； test

R語言主要诞生于上个世纪九十年代，最初是S语言的一种实现。R是由来自于新西兰奥克兰大学的Ross Ihaka和Robert Gentleman开发（也因此称为R），现在由“R开发核心团队”负责开发[1]。它的主要特点是具备一系列连贯而又完整的数据分析中间工具，拥有一整套数组和矩阵操作运算符能有效地处理保存数据，其图形统计功能可以对数据直接进行分析和显示，加上R是一种面向对象的可编程语言，和其他编程语言、数据库之间有很好的接口[2]。

R语言能够提供强大的统计分析、数据处理以及图形可视化功能。与其说R是一种软件，不如说R是一种统计应用的环境。另外R语言还是一个完全免费的统计软件，许多程序员提供了大量丰富的程序包，并且拥有强大的社区资源，有许多不同领域的专家、学者在此处交流与探讨。正因如此，R语言在国外的统计教学及科研工作中已经得到了广泛应用，但是在国内，R语言还比较陌生，研究人员相对较少。不过可喜的是，已经有不少学者已经在关注R语言，并为推广和使用R语言而努力。

本文就是在此环境之下，介绍R语言的一些简单统计功能，希望能够为广大学者和教学人员提供一些借鉴之处。

1 R语言中的对象与数据类型

R语言把操作对象分为多种类型，如向量、矩阵、因子（factor）、清单（list）及数据框（data frame）等。部分R函数会根据类型的不同而作不同的处理。比如函数plot会随着不同的数据类型而得到不同的结果：输入数字向量，会得到点散图；输入因子，会得到盒形图；输入回归模型分析则得到图像分析。这种处理方式在R中被称为“对象导向式程序编写”[3]。

1.1 标量与向量

标量是由简单的数字或者字符串所组成的，如果是字符串，则在左右两端需加上双引号。比如3代表数字，而“3”则代表一个符号。向量则是一组一维标量的集合。如果一个向量同时包含了数字和字符，则R语言会统一按照文字处理。例如：

> a=c（1，2，3，4，"f"）

1.2 矩阵

矩阵就是二维的向量，输入矩阵和输入向量类似。例如：

> matrix（c（1：9），nrow=3，ncol=3，byrow="T"）

[，1] [，2] [，3]

[1，] 1 2 3

[2，] 4 5 6

[3，] 7 8 9

这里输入的3行3列的一个矩阵，byrow="T"表示是按照行进行排列矩阵。如果是一行的矩阵，就可以按照向量进行处理了。

1.3 清单

清单可以将多种类型的数据放在一起。如果将向量看作是一组标量的排列，则清单可以理解为一组不同形态对象的排列。例如：

> b=list（c（"one"，2，3，"four"）， matrix（c（1，2，3，4，5，6，7，8，9）， nrow=3， ncol=3）， c（3，9，15））

想输出第一组内容，可以使用：

> b[[1]]

[1] "one" "2" "3" "four"

如果输入：> b[[2]][1：3，2]，则显示的是矩阵中第二列的内容。

2 R的统计功能

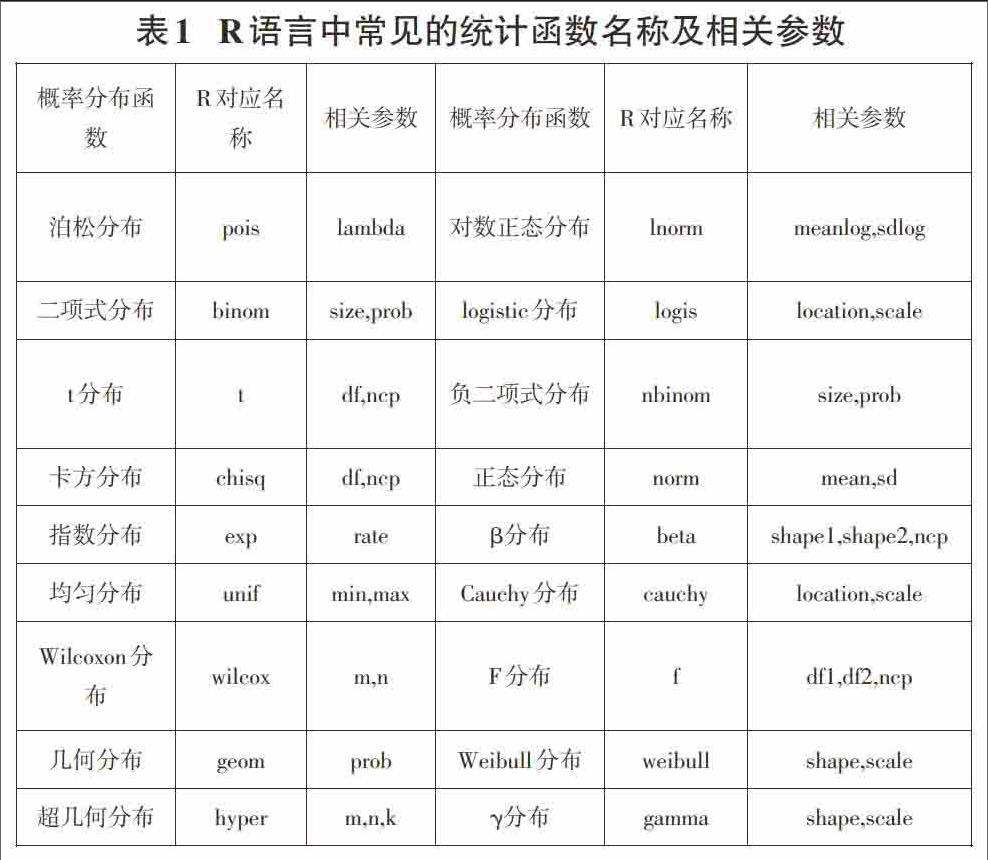
R语言中内置了许多统计函数，用这些函数可以方便地实现大量的统计功能，方便地解决在统计中概率计算、临界值、分位数等问题。表1是R语言中常见的统计函数名称及相关参数。

为了便于方便理解，R将统计分布设为四个基本项目，即概率密度函数、累积分布函数、分位数和伪随机数[3]。每个统计函数所对应的项目函数，其命名规则是用d、p、q、r做为名称前缀。比如几何分布函数，R语言对应名称为geom，则可以用dgeom、pgeom、qgeom、rgeom去表示几何分布的这四个基本项目。

下面举一个例子表明R语言对于统计函数的处理方法，简单的例句及释义如下：

> pnorm（5） #计算标准正太随机变量Z<5的方差

> pnorm（5，3，1.2） #计算正太随机变量平均数是3，标准方差是2，分布函数<5的概率

> pnorm（5，3，1.2）-pnorm（4，3，1.2） #求分布函数4～5之间的概率

> qnorm（0.85，3，1.2） #求85%的分位数

> dnorm（4，3，1.2） #求值为4时的概率密度

> rnorm（20，3，1.2） #产生20个随机数

如上可以看出，对于相关的函数，只需要在前面加上相应的前缀，就可以进行计算了，非常方便。表1中列举的其它函数也可以以此类推。

3 R与概率曲线

3.1 正态分布

正态分布是统计学中最重要、最常见的分布之一，现实生活中的很多随机现象都可以用正态分布或类似正态分布进行描述。正态分布对于统计学中的三大抽样分布具有引导作用。对于正态分布，可以用下面语句画出整体曲线：

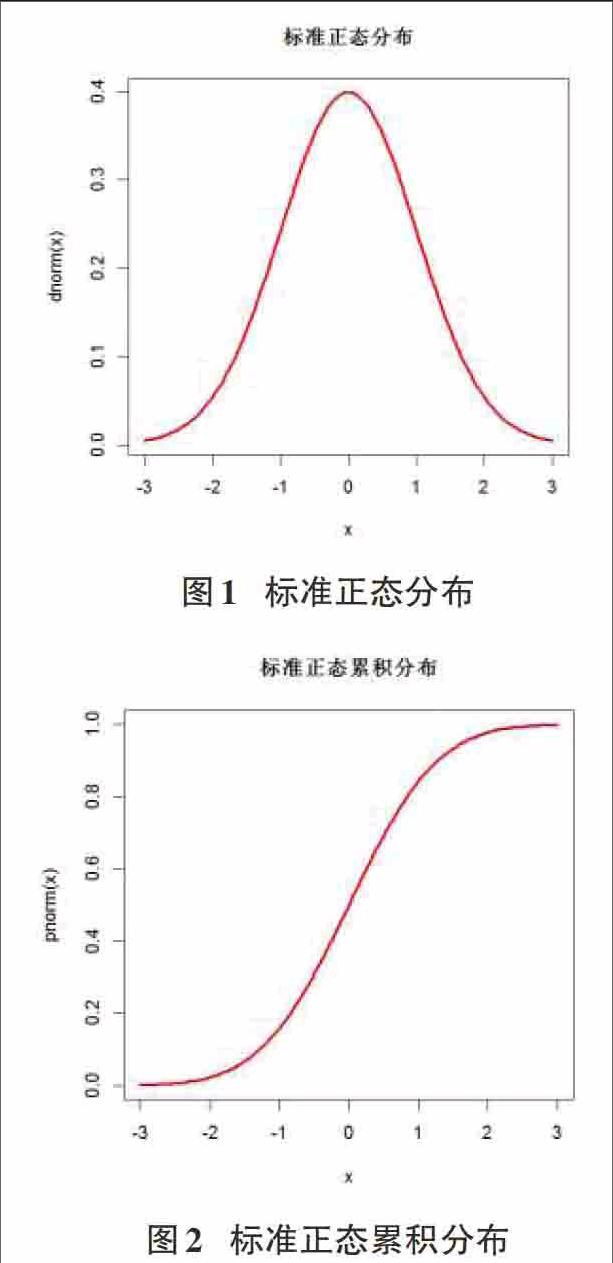
> curve（dnorm（x）， xlim=c（-3，3），col="red"， lwd=3， lty=1，main="标准正态分布"）

其中，curve是绘画曲线的常用命令，是根据（x，dnorm（x））的坐标关系作出的。横轴的取值范围为-3，3，曲线颜色为红色，线条宽度3，main的内容为图形标题。如果想改为累积分布函数，则按照上面第2点所叙述，只需要将dnorm函数改为pnorm即可，语句如下：

> curve（pnorm（x）， xlim=c（-3，3），col="red"， lwd=3， lty=1，main="标准正态累积分布"）

做出的图形分别如图1和图2所示。

这里再举一个例子，对于正态分布进行简单模拟。

假设正态分布样本数目为5000，进行模拟后画出正态分布曲线和样本直方图，所用语句如下：

> n=5000 #设定样本数目

> x=rnorm（n） #产生伪随机样本

> curve（dnorm（x）， xlim=c（-3，3），col="red"， lwd=3， lty=1） #画出标准正态分布曲线

> hist（x，probability=T，add=T） #画出直方图

> lines（density（x），col="red"， lwd=3， lty=2） #在图上添加x的模拟密度曲线

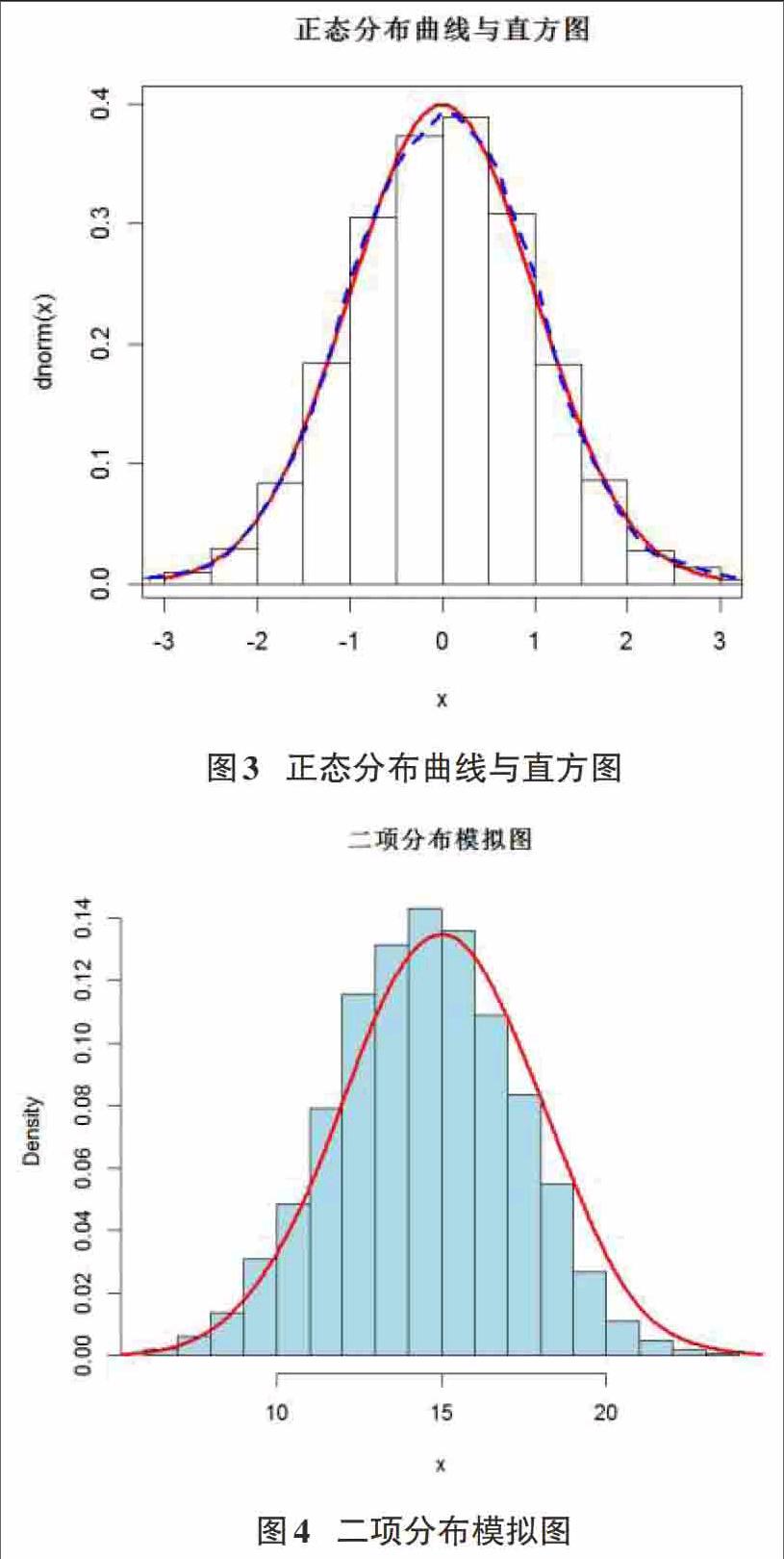
> title（main="正态分布曲线与直方图"） #添加图表标题

所做图形如图3所示。由图可以看出，所产生的模拟曲线与标准正态分布曲线是比较吻合的，如果样本空间越大，则吻合度越高。

3.2 二项分布

二项分布与贝努力实验有着极大的联系。一个实验中有两个实验：成功（记为1）与失败（记为0），出现的概率分别为p和1-p，则一次实验 （称为贝努力实验） 成功的次数服从一个参数为p的贝努力分布。如果将实验次数重复n次，则实验成功的次数服从参数为（n，p）的二项分布。所以当二项分布实验为1时，就是贝努力分布。

现在假设二项分布参数为f（n，p） n=30，p=0.5的计算机模拟。由贝努力实验与二项分布的关系可以将此过程设计为：

> n=30 #设置f（n，p）中n的值为30

> x=c（1：5000） #将实验过程模拟为5000次，并将x保存为一个长度为5000的向量记录实验结果

> for（i in 1：5000）{x[i]=sum（sample（c（0，1），n，replace=T））} #设置循环过程，在等概率抽样条件下，将每次试验中1出现的次数赋值给相应的X向量。

> hist（x，col="light blue"， xlim=c（min（x），max（x））， probability=T， main="二项分布模拟图"） #画出X的频率直方图，并添加图表标题

> lines（density（x，bw=1），col="red"，lwd=3） #添加模拟分布密度曲线

画出的图形如图4所示。由此可以看出频率直方图及模拟的密度曲线与标准的正态分布曲线还是比较相似的[4]。如果根据中心极限定理，当随机变量足够大时，正态分布与二项分布是非常接近的。

4 R语言与统计检验

在数理统计分析中，只能由估计量估计总体的参数，总体参数始终是不可知的，只能通过统计检验，由统计量推断总体参数[5]。一般在统计推断过程中，对参数先提出假設，然后根据假设进行假设检验。在R语言中包含了多种参数假设办法。下面举一个检验的例子。

某种元件的寿命X（以小时计算）服从正态分布Ν（μ，σ2），现测得16只元件的寿命如下：

149 260 485 210 239 280 191 212

224 379 179 264 222 362 198 250

假设显著性水平a=0.05，问是否可以认定元件的平均寿命不大于225小时？

分析：这是一个关于均值的检验问题，可以采用单边检测方法，需要检验

由于总体方差未知，故采用t-检验方法。检验统计量公式为：

在a=0.05前提条件下，样本数量n=16，临界值t1-a（n-1）=1.7531，则拒绝域{t> 1.7531}，根据公式计算X平均值=256.5，样本方差s=86.02，所以t=（256.5-225）/（86.02/）=1.4648，因此样本离差t=1.4648小于临界值1.7531。因此接受原假设，可以认为元件的平均寿命不大于225小时。

而在R语言中，计算上述问题只需要下面两个步骤就可以了。

> X=c（149，260，485，210，239，280，191，212，224，379，179，264，222，362，198，250）

> t.test（X，mu=225，alternative='greater'）

得出结果为：

One Sample t-test

data： X

t = 1.4648， df = 15， p-value = 0.0818

alternative hypothesis： true mean is greater than 225

95 percent confidence interval：

218.8023 Inf

sample estimates：

mean of x

256.5

在这里没有给出结论，但是可以得出t值和p值，从p而判断是否拒绝原假设。如果从p值判断，得出p值为0.0818>0.05，不能拒绝原假设。则接受H0，因此在a=0.05情况下，可以认为平均寿命不大于225小时。t值的结果与判断方式和前面所述一样。另外参数alternative可以为“less”，“greater”和“two side”，可以反映出假设是单边假设还是双边假设，默认是双边假设。

5 结束语

R语言语法简单，容易编写。通过文本的叙述，相信读者对R语言已经有了一定的了解。本文所叙述的只是R语言的一小部分内容，读者可以通过查看相关参考资料对R语言做进一步的掌握。另外由于R语言是开源软件，自由免费，非常适合做统计分析和教学。在目前注重知识产权的大背景下，掌握和利用好R语言对于统计分析具有重大的现实作用。

参考文献：

[1] smalllleopard. R语言为Hadoop集群数据统计分析带来革命性变化[EB/OL]. （2012-11-10）. http：//blog.sina.com.cn/s/blog_6cfc336b01018wvt.html.

[2] 陳希. 基于R语言数据挖掘的社交网络客户细分研究[D]. 北京： 北京邮电大学， 2011： 34-40

[3] 陈毅恒， 梁沛霖. R软件操作入门[M]. 北京： 中国统计出版社， 2006.

[4] 叶文春. 浅谈R语言在统计学中的应用[J]. 中共贵州省委党校学报， 2008（4）： 123-125.

[5] 薛毅， 陈立萍. 统计建模与R软件[M]. 北京： 清华大学出版社， 2007.