基于RSA的动态ID远程用户认证协议分析

翟靖轩+徐玉林+王大阜

摘要：基于口令和智能卡的双因子远程用户身份认证已经成为保障公共网络数据安全的重要手段之一，可用于在线支付和在线医疗等领域。为解决Tsai等提出的方案存在的不能提供前向安全、存在内部攻击和拒绝服务攻击等缺陷，Ma等基于RSA密码体制提出了一种动态ID身份认证协议。简要回顾了Ma等的方案，并进行了安全性分析。分析结果表明Ma等的方案仍然存在不能抵抗离线猜测攻击、不能提供前向安全性等缺陷，并给出了具体攻击步骤。

关键词：认证；RSA；分析；智能卡；口令

中图分类号：TP309.08 文献标识码：A 文章编号：1009-3044（2017）01-0031-04

Abstract： Two-factor remote user authentication scheme based on password and smart card is the most popular way to protect secure data exchange over insecure channel. It can be used in online payment system and online medical system. Tsai et al. proposed a dynamic ID authentication scheme， which is vulnerable to denial of service attack and insider attack. To overcome these security flaws， Ma et al. propose an enhanced dynamic ID-based authentication scheme based on RSA. This paper reviews Ma et al.s authentication scheme and conduct a cryptanalysis. The analysis shows that the Ma et al.s scheme is still vulnerable to an offline guessing attack and unable to provide the forward secrecy. Then the concrete attack steps are given correspondingly.

Key words： authentication； RSA； cryptanalysis； smart card； password

1 背景

随着互联网技术的快速发展，针对远程用户的身份认证技术已经成为保证信息安全的重要手段之一。远程身份认证可用于在线支付[1]和在线医疗[2]等领域，是一种常用的保护合法用户安全的访问远程服务器的方法。基于口令的身份认证协议由于口令简单易记、使用便捷和无需额外设备支持等特点，已成为一种应用普遍的身份认证协议。1981年Lamport[3]提出了在不安全的通信中，采用口令表认证远程用户的方案。在Lamport的方案中，一旦口令表被恶意用户窃取，系统毫无安全性可言。此外，维护口令表的资源开销也较大。为了解决这一问题，2000年Hwang等[4]提出了一种基于智能卡的远程身份认证方案，Hwang等的方案不需要在服务器保存口令表，但Hwang等的方案被验证是不安全的。此后，研究人员提出了大量的协议用于增强身份认证的安全性和提高效率。为提高安全性，研究人员采用了双因子技术来加强身份认证的安全性。双因子身份认证，通常是将“用户所知道的”和“用户所拥有的”这两个认证因子结合使用。基于智能卡和口令的双因子认证协议是研究热点之一，大量基于智能卡的双因子认证协议被提出，主要包括：基于椭圆曲线密码机制[5]、基于混沌密码机制[6]、基于ElGamal密码机制[7]和基于RSA密码机制[8] 等。其中，基于RSA的双因子认证技术，由于加密运算量小非常适合在远程身份认证协议中使用[8]。在计算能力相对较弱的客户端执行加密操作，在计算能力较强的服务器端执行解密操作。

早期的智能卡与口令双因子认证方案中，用户的身份（ID）是靜态的。当攻击者控制通信信道后，身份ID很容易被攻击者从登录消息中获取，从而导致用户被追踪，不能满足身份匿名的安全需求。这在很多身份隐私要求较高的系统中是不可行的，如在线医疗系统中，必须确保病人的身份信息不被泄露。2004年Das等[9]首次提出了基于智能卡的动态身份认证协议，Das等宣称他们的协议可以达到用户匿名。然而，Das等的协议是不安全的，不能实现身份匿名、容易遭受拒绝服务攻击和离线猜测攻击，协议也没有提供用户和服务器之间的双向认证。此后，为提高动态身份认证协议的安全性，研究者们又开展了大量工作。Wang等[10]提出了一种动态身份认证协议，并宣称他们的方案在保持了Das协议特性的基础上，更为安全和有效。Tsai等[11]指出Wang的方案不能提供用户匿名，不能抵抗仿冒攻击，并提供了一种改进的方案。Ma等[12]指出Tsai的方案不能提供前向安全，并存在内部攻击和拒绝服务攻击。为了解决Tsai方案的缺陷，Ma等提出了一种基于RSA的动态ID口令认证协议，宣称他们的方案可以抵抗离线口令猜测攻击、仿冒攻击、拒绝服务攻击、重放攻击和并行会话攻击等，并达到前向安全、用户匿名和双向认证等目标。然而，我们的分析指出Ma等的方案依然不能提供前向安全，并容易遭受离线猜测攻击。

本文结构安排如下。第2节给出了安全假设模型和定义，第3节简单回顾了Ma等提出的方案，第4节分析了Ma等的提出方案并指出了存在的问题，第5节是结束语。

2 预备知识

本节给出了基于智能卡和口令的动态ID认证协议相关知识和安全假设模型。本文所分析协议安全的安全假设模型基于Dolev-Yao模型[13]拓展，协议采用RSA密码机制设计。相关定义及模型描述如下：

2.1 安全假设模型

协议的安全模型，攻击者可以执行的操作和不具有的能力描述如下：

1）攻击者可以监听、拦截、重放和修改公开信道中的任何消息。也可以是一个合法的内部用户，如服务器或系统中的用户。

2）攻击者在公开信道中可以冒充服务器和任何用户向其他实体发送消息。

3）攻击者可以窃取用户的智能卡，并采用边信道攻击方法获取智能卡中的所有秘密参数。

4）用户的身份ID和口令是一个有限的空间，可被攻击者在获取一定秘密参数的前提下，采用离线猜测方法获取。但秘密数字和随机数是一个足够大的空间，攻击者无法猜到。攻击者也无法从公钥猜测到私钥。

5）没有正确的密钥，攻击者无法从给定的密文中恢复出明文。

6）攻击者无法控制私有通信。

2.2 RSA公钥密码体制

RSA是一种常用的加密算法，由Rivest、Shamir和Adleman于1977年发布。RSA是基于大整数因子分解困难问题而设计，即给定两个大素数p、q，计算n = pq是容易的。相反，给定大整数n，求其素因子p、q是困难的。RSA公钥密码体制介绍如下：

1）参数定义与密钥生成

step1：首先秘密选择两个大素数p，q，计算n = pq；

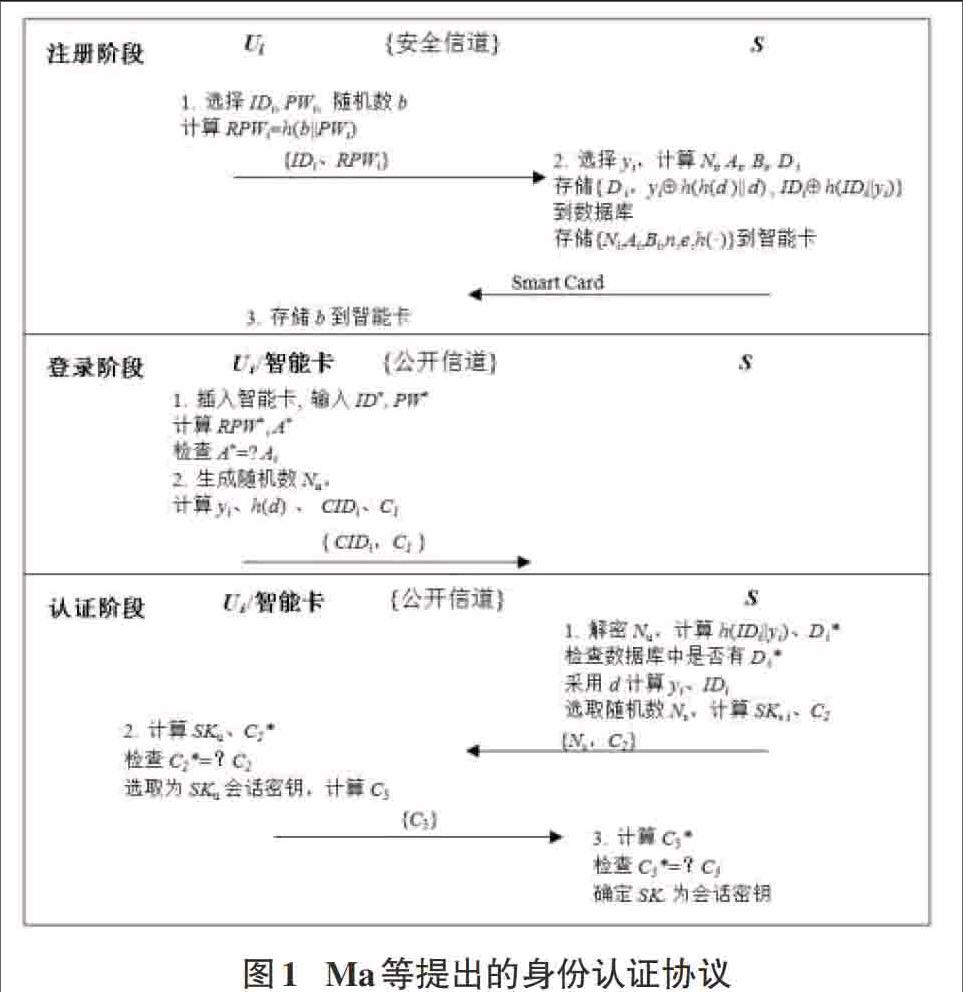
step2：计算欧拉函数φ （n） = （p-1）（q-1），随机选择一个整数e，满足1

step3： 公开（e，n）作为公钥，并保持p、q和d为秘密数。

2）加密与解密算法

设明文为m，密文为c，加密及解密算法如下：

加密：c = me mod n

解密：m = cd mod n

2.3 相关定义

本文分析协议所使用的定义描述如下：

l Ui：第i个用户

l S：服务器

l ：攻擊者

l IDi：用户i的身份

l PWi：用户i的口令

l n：n=pq，p、q是两个不同的大素数

l d：服务器的私钥

l e：服务器的公钥

l |ID|：用户的身份空间

l |PW|：用户的口令空间

l h（·）：哈希函数

l ：异或操作

l ||：连接操作

3 Ma等的方案回顾

Ma等[9]提出身份认证方案包括4个阶段：1）注册阶段；2）登录阶段；3）认证阶段；4）口令更改阶段。其中，每个用户只有执行注册后才可以使用系统，注册阶段每个用户只执行一次，而且是在安全通信的环境中执行。图1列出了注册阶段、登录阶段和认证阶段的协议执行过程。

3.1 注册阶段

服务器初始化时根据RSA密码机制，先选取两个安全的大素数p和q，并计算n=p*q。随后选择一个e，并计算相应的d，满足ed ≡ 1 mod φ （n）。最后，服务器公开n和e作为公钥，并保持p、q和d为秘密数。

当用户Ui在系统注册时，执行以下过程：

Step1：用户Ui选择身份IDi、密码PWi和一个随机数b，并计算RPWi=h（b||PWi），然后通过安全信道发送{IDi、RPWi}到服务器。

Step2： S选择一个随机数yi，并计算Ni = h（IDi || RPWi） h（d），Ai=h（RPWi|| IDi）， Bi=yi IDiRPWi，D i= h（h（IDi||yi） h（d））。S存储{ D i ，yi h（h（d ）|| d） ， IDi h（IDi||yi）}到数据库。随后，S存储{Ni，Ai，Bi，n，e，h（·）}到智能卡并通过安全方式发送给用户Ui。

Step3：当Ui收到智能卡后，存储b到智能卡。

3.2 登录阶段

当用户Ui登录系统时，执行以下过程：

Step1：用户Ui插入智能卡，输入ID*和PW*，智能卡计算RPW*= h（b||PW*），A*=h（RPW*|| ID*）。智能卡检查A*是否等于存储在智能卡里的Ai，如果A*Ai，智能卡拒绝用户登录。

Step2：智能卡生成随机数Nu，计算yi = Bi ID*RPW*，h（d）= h（ID*|| RPWi） Ni，CIDi= h（ID*||yi） h（h（d） ||Nu） ，C1=Nuemod n。Ui发送登录消息{ CIDi，C1 }到服务器S。

3.3 认证阶段

当服务器S收到Ui的登录请求后，执行以下步骤：

Step1：服务器S首先使用私钥d从C1中解密出Nu，计算h（IDi||yi） = CIDi h（h（d） ||Nu），D i*= h（h（IDi||yi） h（d））。然后，服务器S检查数据库中是否有对应的D i*，如果没有，服务器S拒绝用户Ui的登录请求。否则，S从数据库中提取出对应的yi h（h（d ）|| d） ， IDi h（IDi||yi），采用d计算yi =（ yi h（h（d ）|| d） ） h（h（d ）|| d），IDi=（ IDi h（IDi||yi） ） h（IDi||yi）。最后，服务器选取一个随机数Ns，计算SKs= h（IDi|| yi ||Nu||Ns||CIDi），C2= h（yi || IDi ||SKs），S发送响应消息{Ns，C2}到Ui。

Step2：当用户Ui收到{Ns，C2}后，Ui首先计算SKu= h（IDi|| yi ||Nu||Ns|| CIDi），C2*= h（yi || IDi ||SKu），比较C2*是否等于C2。如果相等，Ui选取SKu为会话密钥，并计算C3= h（Nu||Ns|| yi || IDi || SKu），发送{C3}到服务器S。

Step3：服务器S收到{C3}后，计算C3*= h（Nu||Ns|| yi || IDi || SKs），比较C3*是否C3等于。如果相等，服务器S确定SKs为会话密钥。

3.4 口令更改阶段

Step1：用户Ui插入智能卡，输入IDi、原密码PWi和新密码PWnew。首先，智能卡计算RPW*= h（b||PWi），A*=h（RPW*|| IDi）。智能卡检查A*是否等于存储在智能卡里的Ai，如果A*Ai，智能卡拒绝用户Ui修改密码。

Step2：智能卡计算Nnew= Ni h（IDi||h（b||RPW*））h（IDi || h（b || PWnew）），Anew=h（h（b||PWnew）|| IDi）， Bnew= BiRPW* h（b || PWnew）。然后，智能卡用{Nnew，Anew，Bnew }替换{Ni，Ai，Bi }。

4 Ma等的方案分析

本节分析了Ma等的方案，指出方案存在不能抵抗离线猜测攻击、不能达到前向安全性的设计缺陷，并给出了具体攻击步骤。

4.1 不能抵抗离线猜测攻击

Ma等的方案不能抵抗离线猜测攻击。当攻击者窃取了合法用户的智能卡后，可以通过边信道攻击方法获取到智能卡中的秘密参数Ai，从而执行离线猜测攻击，获取合法用户的身份ID和密码PW。攻击步骤如下：

Step1： 攻击者从身份空间|ID|选取一个身份ID*，从用户的口令空间|PW|选取一个口令PW*；

Step2：攻击者计算，A*=h（h（b||PW*）*||ID*）；

Step3：攻击者比较A*是否等于智能卡中的Ai。如果不相等，重复执行Step1和Step2，直到正确猜解出用户相应的身份ID和口令PW。

与密钥空间和随机数空间不同，用户的身份空间|ID|和用户口令空间|PW|通常不是非常大。攻击者的搜索空间为|ID|×|PW|，能够在多项式时间内完成身份和口令的遍歷，从A*中猜测出正确的身份IDi和口令PWi。因此，Ma等的方案不能抵抗离线猜测攻击。

4.2 不能提供前向安全性

身份认证协议的前向安全性是指当攻击者获取了服务器S的长期私钥d等私密信息，并获取了用户和服务器在公开信道传输的所有信息，之前的会话密钥SK仍然是安全的。我们的分析表明，Ma等的方案不能确保前向安全性。

当攻击者获取了服务器的长期私钥d，窃取了服务器中的数据库{ Di，yi h（h（d ）|| d） ， IDi h（IDi||yi）}，记录了之前的通信消息{CIDi，C1}和{Ns，C2}。执行攻击步骤如下：

Step1：攻击者从通信中获取{ CIDi，C1 }，解密Nu= C1dmod n，计算Di*= h（CIDi h（h（d） ||Nu）） h（d）），使用从Di*数据库中提取对应的yi h（h（d ）|| d） ， IDi h（IDi||yi），采用d计算yi =（ yi h（h（d ）|| d） ） h（h（d ）|| d），IDi=（ IDi h（IDi||yi） ） h（IDi||yi）。此步骤执行完成后，成功获取到了CIDi、Nu、IDi和yi。

Step2：攻击者从服务器发送给用户的消息中获取到Ns，再利用Step1中获取的参数，成功计算出对应的会话密钥SK= h（IDi|| yi ||Nu||Ns|| CIDi）。

执行完以上攻击步骤后，攻击者成功计算出之前的会话密钥，从而可以解密用户和服务器之间已经完成的通信。因此，Ma等的方案不能提供前向安全性。

5 结束语

基于智能卡的双因子认证协议是保障数据安全，保护用户隐私的重要手段。如何设计采用公钥技术的双向认证和密钥协商协议是学术界研究的热点之一。本文回顾了基于智能卡和口令的身份认证协议发展历程，总结了智能卡身份认证协议设计时需关注的问题：智能卡中的秘密信息可被攻击者获取，保证身份匿名是信息系统的重要目标。列出了设计基于RSA的动态ID身份认证协议所需的相关知识，简要地回顾了Ma等提出身份认证方案。最后对Ma等的方案进行了安全性分析，指出了Ma等的方案存在的不能抵抗离线猜测攻击，不能提供前向安全等缺陷。这两个安全需求，也是今后设计安全的身份认证协议需考虑的重要因素。

参考文献：

[1] 王菁， 邬书跃， 梁欣. 一种安全高效的在线移动支付协议[J]. 计算机工程与应用， 2013， 49（16）： 82-85.

[2] Cao T， Zhai J. Improved Dynamic ID-based Authentication Scheme for Telecare Medical Information Systems[J]. Journal of Medical Systems， 2013， 37（2）： 1-7.

[3] Lamport L. Password authentication with insecure communication [J]. Communications of the ACM， 1981， 24（11）： 770-772.

[4] Hwang M S， Li L H. A new remote user authentication scheme using smart cards [J]. IEEE Transactions on Consumer Electronics， 2000， 46（1）： 28-30.

[5] 石亚娟， 黄辉辉， 陈建华. 基于智能卡的动态身份认证协议[J]. 电子技术应用， 2015， 41（3）： 97-100.

[6] Zhu H， Hao X. A provable authenticated key agreement protocol with privacy protection using smart card based on chaotic maps[J]. Nonlinear Dynamics， 2015， 81（1-2）： 311-321.

[7] Maitra T， Obaidat M S， Amin R， et al. A robust ElGamalbased password authentication protocol using smart card for client server communication[J]. International Journal of Communication Systems， 2016.

[8] 汪定， 王平， 李增鵬，等. 可证明安全的基于RSA的远程用户口令认证协议[J]. 系统工程理论与实践， 2015， 35（1）：191-204.

[9] Das M L， Saxena A， Gulati V P. A dynamic ID-based remote user authentication scheme[J]. IEEE Transactions on Consumer Electronics， 2004， 50（2）： 629-631.

[10] Wang Y， Liu J， Xiao F， et al. A more efficient and secure dynamic ID-based remote user authentication scheme[J]. Computer Communications， 2009， 32（4）： 583-585.

[11] Tsai J L， Wu T C， Tsai K Y. New dynamic ID authentication scheme using smart cards[J]. International Journal of Communication Systems， 2010， 23（12）： 1449-1462.

[12] Ma C， Wang D， Zhao P， et al. A new dynamic ID-Based remote user authentication scheme with forward secrecy[C]. International Conference on Web Technologies and Applications. 2012：199-211.

[13] Dolev D， Yao A. On the security of public key protocols[J]. IEEE Transactions on information theory， 1983， 29（2）： 198-208.