集装箱起重机强震非线性动力模型及损伤研究

陈晓林,刘 渊

(1.钦州学院 工程训练中心,广西 钦州535000; 2.广西高校临海机械装备设计制造及控制重点实验室培育基地,广西 钦州 535000)

集装箱起重机(岸桥)的大型化使其结构质量显著增加,重心位置增高,在遭受强烈地震作用时,表现出明显的非线性特征,如下层门腿结构的低周循环屈曲变形[1-2].非弹性变形导致结构滞回特性中强度和刚度退化以及高耸结构在大变形中的P-Δ效应,将直接影响结构弹塑性响应和地震延性需求分析[3].在研究岸桥结构的抗震性能方面,国外如Jacobs等[4-5]采用数值有限元分析,研究现代集装箱起重机弹塑性地震响应,并用1∶10比例的试验模型与研究结果进行比较[6];Kosbab等[7-8]建立了有限元数值模型,定量计算了集装箱起重机地震动态特性.国内金玉龙等[9]对集装箱起重机的抗震可靠性采用数值模拟,并对结构进行地震响应分析计算;郑培等[10-11]采用数值和模型(1∶15)试验方法,考察了集装箱起重机地震波时程的响应;李哲等[12-13]从数值仿真和畸变相似模型试验,进行岸桥地震行为动力学研究.上述研究提出了岸桥抗震设计相关建议和模型设计方法,但数值分析多采用双线性或理想弹塑性恢复力模型,鲜有考虑岸桥结构循环荷载下复杂的非线性滞回特性或P-Δ效应的影响.试验误差和数值计算也表明结构滞回因素对弹塑性地震响应影响较大.

在岸桥弹塑性地震响应分析中,关键问题是建立反映结构滞回因素的计算模型.经典Bouc-Wen模型较真实地描述刚度退化、强度退化和塑性硬化等滞回特性.Goda等[14]利用经典单轴Bouc-Wen模型,对非弹性单自由度体系(SDOFS)进行研究,发现强度和刚度退化效应可以明显增大非弹性体系的地震延性需求,但其未考虑P-Δ效应的影响.童根树等[15]在研究结构在强震作用下发生大变形时,发现P-Δ效应往往比较明显.相比在弹性变形下,P-Δ效应会导致结构屈服后的刚度下降,增大侧向非弹性变形.

鉴于岸桥的自身结构特点和大型港口起重设备在抗震安全设计中突显的重要性,本文基于一种单轴Bouc-Wen模型,建立岸桥结构的等效SDOFS,研究其双向地震载荷作用下非弹性动力响应;并与采用理想双线性恢复力模型的单自由度体系,通过Wilson-θ方法编程计算的结果进行对比验证.通过综合考虑结构P-Δ效应、屈服硬化、强度和刚度退化等滞回特性因素,明确其对大型港口集装箱起重机结构地震延性需求及结构损伤评估的影响.

1 集装箱起重机动力模型研究

国外某公司[1-2]数值和试验研究及笔者前期的研究[12-13]表明,岸桥地震动行为的一般规律为结构非弹性变形主要集中在门架结构上部位置,图1所示P1点.以竖向层来看,岸桥为竖向刚度不规则结构,底层门架结构的侧向刚度较小,海、陆侧立柱与门框横梁产生的相对位移明显较大,以各层最大位移角标定,如图2所示.岸桥弹塑性动力时程分析中某一时刻的应力分布,如图3所示.

图1 岸桥结构模型及地震波加载方式Fig.1 Structural model of container crane and loading mode of seismic wave

图2 岸桥时程分析应力分布Fig.2 The stress distribution of container crane’s time history analysis

图3 岸桥竖向层P点最大位移角Fig.3 Container crane’s maximum displacement angle of the vertical layer P point

本文选取的是国内某公司的一种大型岸桥结构,主要参数:大车轨距D为35 m,门腿上横梁高度L为17.5 m,重心高度H为45.7 m,集装箱起重机的额定起重质量为70 t,自重约为1 500 t.限于篇幅,这里给出模态分析结果:结构反应以第3阶模态水平振型为主,有效模态质量参与比λ=89.4%,水平方向自振频率f=0.46.

由岸桥地震动响应行为的一般规律可知,其多自由度体系结构(MDOFS)的非线性地震动力学行为,可以表征为等效单自由度体系(SDOFS)的动力时程响应,如图4所示.假定岸桥结构水平位移反应始终与岸桥的水平振型成比例,其多自由度体系可以通过解耦并等效成单自由度体系[16].

图4 岸桥等效单自由度体系(SDOFS)Fig.4 The equivalent single degree of freedom system

本文在等效简化的基础上,考察前述滞回因素影响下的岸桥底层门架结构薄弱层的地震动响应规律.不失一般性,等效的岸桥单质点模型考虑双向地震波激励,如图5所示.竖向地震波激励和重力产生的P-Δ效应可以等效为在门架横梁处,即上文中P1点位置的弯矩为

(1)

图5 等效SDOFS的水平位移反应Fig.5 Horizontal displacement reaction of the equivalent SDOFS

将M0考虑成水平方向上作用于基底和集中质量上的一对力偶,则等效水平力为

(2)

式中:L为门架横梁高度.

根据动力平衡原理,岸桥等效单自由度体系(SDOFS)的运动微分方程如下:

(3)

2 Bouc-Wen模型及控制参数分析

在弹塑性时程分析中,采用新型Bouc-Wen模型来描述岸桥结构SDOFS的恢复力和位移滞回特性,则结构恢复力F(u)可以表示为[17]

F(u)=αku+(1-α)kz

(4)

式中:α为屈服后刚度系数;k为SDOFS的弹性刚度;z为非线性滞回位移.其中u和z之间存在以下关系:

(5)

(6)

由推覆分析可以得到岸桥等效单自由度体系(SDOFS)的屈服力fy和屈服位移uy,则有uy=kfy,如图6所示.

图6 等效SDOFS的Bouc-Wen模型Fig.6 The Bouc-Wen model of the equivalent SDOFS

引入以下无量纲量:

(7)

将式(3)～(6)进行归一无量纲化处理得

(8)

μf=αμ+(1-α)μz

(9)

(10)

(11)

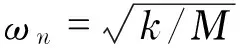
将式(8)～(11)联立,通过Matlab编程求解,可以得到岸桥等效SDOFS的规一化位移时程μ(t)、规一化恢复力时程μf(t)、规一化非线性滞回位移时程μz(t)和规一化累积滞回耗能με.进而可以确定岸桥结构等效SDOFS的地震延性需求μmax和采用Park-Ang定义的地震损伤指标μcDPA:

μcDPA=μmax+δEμε

(12)

式中:μc为岸桥结构的延性能力;δE为循环载荷影响系数,本文取为0.05.

由等效SDOFS的Bouc-Wen模型表达为归一化处理后的公式可知,该模型主要包括以下6个控制参数:{α,n,β,γ,δη,δν}.为更直观表述Bouc-Wen模型中各个参数的物理意义,本文以幅值递增的水平简谐激励对一简单算例进行计算,取算例的基本自振周期Tn=1 s,阻尼比ξ=0.05,结构稳定系数θ=0.1.

由图7可以看出:α为屈服比,当α=0时,Bouc-Wen模型滞回曲线表现为理想弹塑性;当α=0.05时,为双线性弹塑性模型,如图7(a)所示.屈服指数n控制屈服拐点的光滑性,如图7(b)所示,当n取较小值,如n=2时,滞回曲线在拐点处呈光滑过渡;当n=50时,拐点处有明显拐角,近似为理想双线性模型.β和γ为控制滞回曲线中加载和卸载方式参数,如图7(c)所示,当β=0.5,γ=0.5时,模型表现为线性加载和卸载过程;当β=1.5,γ=-0.5时,表现为非线性的加卸载过程.δη和δν分别控制循环加载中滞回曲线在下一次加载过程中强度和刚度的退化效应,如图7(d)和7(e)所示;图7(f)为同时考虑强度和刚度退化效应的滞回曲线.

图7 Bouc-Wen模型参数对岸桥等效SDOFS滞回曲线的影响Fig.7 The influence of the Bouc-Wen parameters on the equivalent SDOFS hysteresis curve

在进行弹塑性时程分析时,Bouc-Wen模型的优点在于对拐点的处理更加方便,且通过调整模型的控制参数,可以综合考虑地震动循环加载时的屈服硬化、强度和刚度退化以及P-Δ效应,较全面地反映钢结构非线性滞回特性的本质特点.

3 动力模型数值计算

3.1 地震波选择与结构非线性

考虑弹塑性状态,从PEER数据库中选择4条典型的强地震动记录.参照建筑抗震设计规范[18],按Ⅷ级和Ⅸ级罕遇烈度,对水平地震波加速度峰值进行调整(PGA=0.4g和PGA=0.62g),竖直(Y向)地震波峰值取为水平(X向)地震波峰值的0.65倍,即0.65×PGA,如表1所示.

表1 地震波参数Tab.1 The parameters of seismic wave

限于篇幅,本文直接给出岸桥结构进行推覆(Pushover)分析和解耦得到的等效SDOFS关键参数[19]:屈服力fy=3.584×106N;屈服位移uy=0.296 m;屈服刚度系数α=0.17.由模态分析得到结构水平方向的自振圆频率ωn=2.89,取一般结构的常用阻尼比ξ=0.05,岸桥结构SODFS的稳定系数θ=0.069.

3.2 与双线性模型计算结果对比

实际中,钢结构一般采用双线性模型描述其材料非线性特征,因此本文采用Bouc-Wen模型与双线性模型,按Wilson-θ法编制结构动力反应图,并对计算结果进行对比验证.在两种计算方法中均考虑结构重力和竖向地震激励的P-Δ效应,并保持与双线性恢复力模型条件的一致性,Bouc-Wen模型控制参数{α,n,β,γ,δη,δν}取值为{0.17,2,0.5,0.5,0,0 },即不考虑退化效应.等效SDOFS采用双线性模型计算的水平位移时程统一按式(7)进行归一化处理,计算结果对比如图8和表2所示.

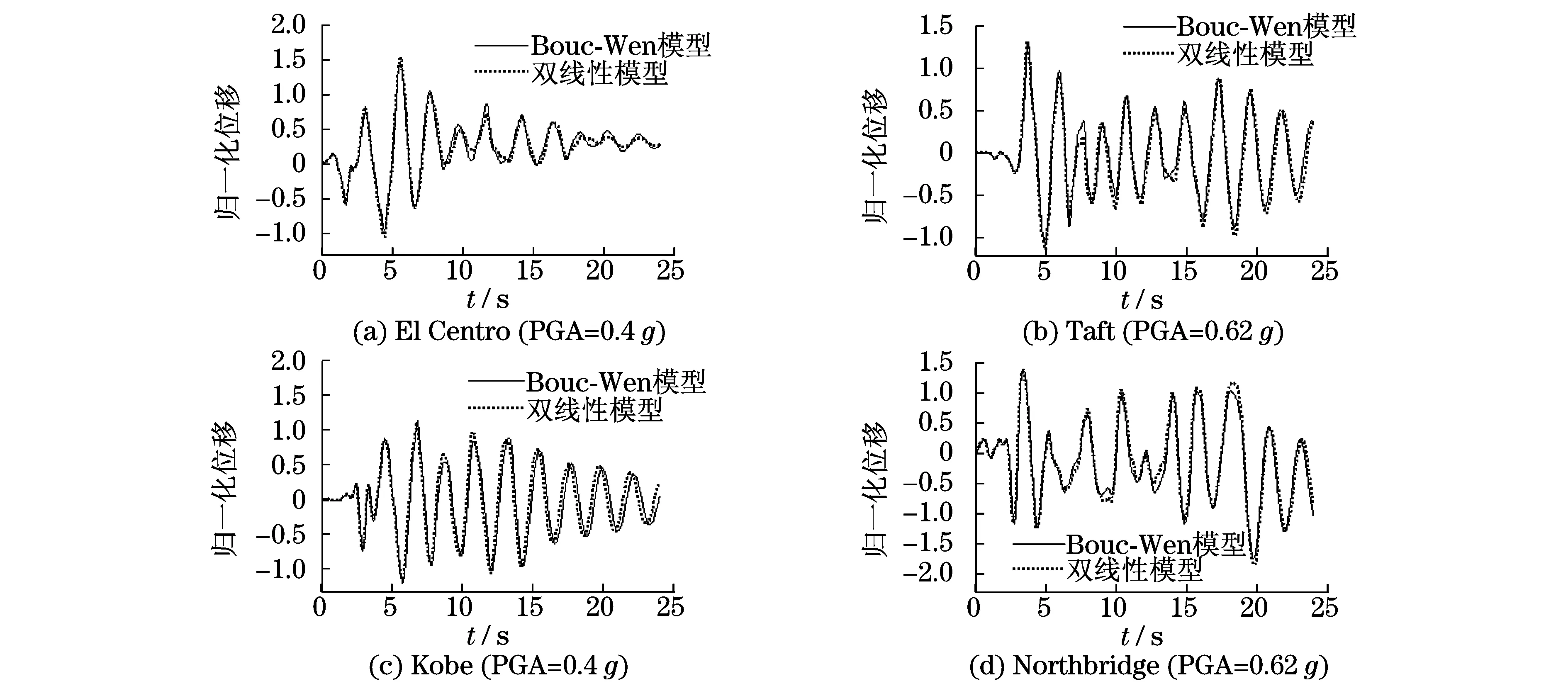
图8 岸桥SDOFS不同地震激励下的归一化位移时程响应对比Fig.8 Comparison of the normalized displacement time response in different seismic excitation of SDOFS 表2 岸桥地震延性需求结果对比Tab.2 Comparison of earthquake ductility demand about SDOFS

地震波加速度峰值PGA/gBouc-Wen模型μmax双线性模型μmax误差/%El-Centro0.4/0.62双向XY1.52/1.761.53/1.750.7/1.2Taft0.4/0.62双向XY0.98/1.311.00/1.322.0/0.8Kobe0.4/0.62双向XY1.15/1.371.18/1.341.4/2.2Northbridge0.4/0.62双向XY1.28/1.761.29/1.820.8/3.4

从对比结果可以看出:岸桥等效SDOFS采用Bouc-Wen模型和双线性模型计算的结果具有较好的一致性,误差在1%～3%左右;对于中小震作用下的岸桥结构响应分析,可以不计退化效应,两种模型均为合理;Bouc-Wen模型对于时变刚度的拐点处理较好.

3.3 P-Δ效应对响应结果的影响规律

本节对岸桥等效的SDOFS采用Bouc-Wen模型计算,分别考察结构自重、竖向地震载荷产生的P-Δ效应对位移时程响应和地震延性需求的影响.其中两种地震波作用下的时程响应对比见图9,结果汇总于表3.图9(a)归一化位移时程响应曲线表明,重力的P-Δ效应会进一步增大结构水平摆动的侧向位移;图9(b)表明重力的P-Δ效应会使结构发生明显的侧移,从而显著增加结构的残余变形,甚至可能造成结构失稳.

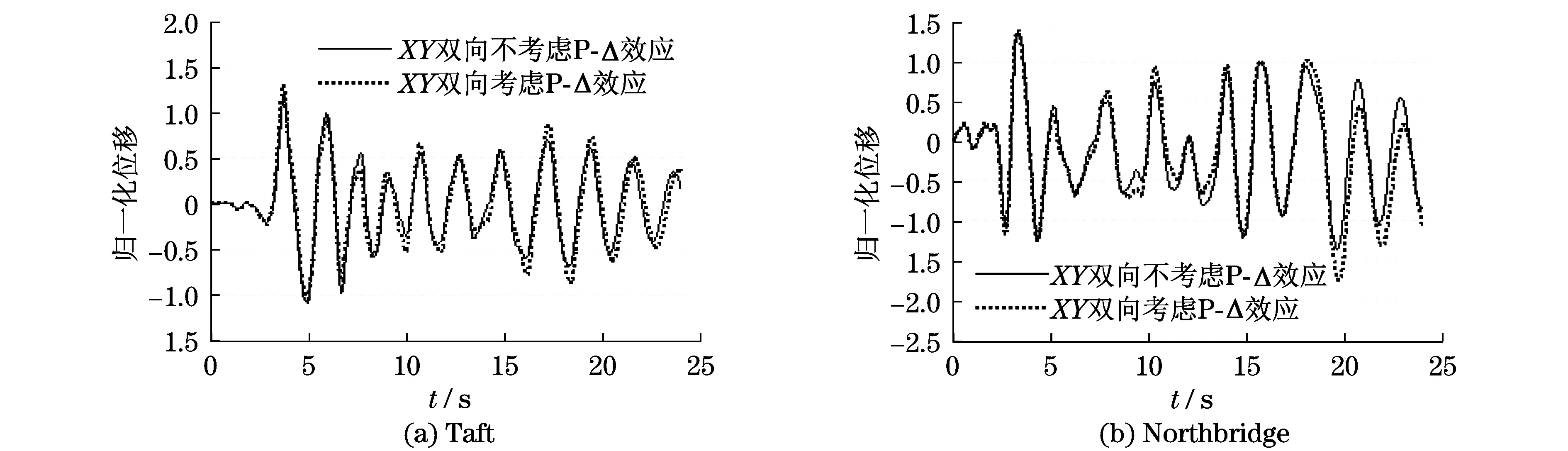
图9 P-Δ效应对岸桥SDOFS归一化位移时程响应影响对比Fig.9 Comparison of the P-Δ effect on normalized displacement time response

从表3可以看出:单向X和双向XY地震激励作用下的对比,竖向地震载荷引起的P-Δ效应对岸桥结构的地震延性需求基本无影响;单向X或双向XY地震激励作用下,由重力造成的P-Δ效应会显著增加结构的地震延性需求.在小塑性变形范围内,是否考虑重力的P-Δ效应误差在8%～10%左右;结构发生较大塑性变形后的影响会在15%以上.

表3 P-Δ效应对岸桥SDOFS地震延性需求的影响Tab.3 The influence of the P-Δ effect on earthquake ductility demand of SDOFS

3.4 滞回因素对损伤的影响

岸桥等效SDOFS的归一化恢复力由式(9)计算,非弹性损伤由式(13)计算.限于篇幅,本节取一种地震波,分析不同非线性滞回因素对结构损伤的影响,考虑以下3种情况的地震损伤指数:工况1为不考虑重力的P-Δ效应和退化效应;工况2为考虑重力的P-Δ效应,但不考虑退化效应;工况3为考虑重力的P-Δ效应和退化效应.

3种工况的滞回曲线如图10所示,损伤指数计算结果见表4.从滞回曲线和计算结果可以看出:Bouc-Wen模型可以描述结构的非线性滞回现象,工况2相比工况1考虑结构P-Δ效应,滞回环的形状较为饱满,结构的非线性损伤程度也更大,地震损伤指数从1.61增大到1.89左右;结合图10(c)可知,在工况3考虑退化效应结构的归一化位移响应会较为增加,伴随着滞回环中结构刚度的退化,损伤指数进一步增加到2.00左右.

图10 3种工况下的滞回曲线Fig.10 The hysteresis curve under three conditions 表4 3种工况下的损伤指数Tab.4 The damage index under three conditions

地震波加速度PGA/g工况μmaxμε损伤指数μcDPANorthbridge0.62双向XY11.492.381.6121.762.551.8931.872.652.00

4 结论

大型岸边集装箱起重机结构,在强震中往往会表现出非线性特征,低周循环变形带来的损伤表现为结构恢复力模型中强度和刚度的退化.在达到极限破坏前,这种反映结构低周循环变形抗力退化,P -Δ效应的恢复力模型是岸桥强震非线性动力响应分析的基础.据此,本文研究结果表明:

(1) 采用Bouc-Wen模型可以较好地描述岸桥等效SDOFS在遭受强震持时下非线性因素的时域演化特征,对于拐点处理具有优越性.

(2) 对于大型岸桥“上刚下柔”型钢结构在强震作用下,结构非弹性变形较大,重力的P-Δ效应在地震延性需求分析中影响较大,而竖向地震载荷引起的P-Δ效应较小.

(3) P -Δ效应、屈服硬化、强度和刚度退化等滞回因素,能够显著增大结构进入弹塑性阶段的地震延性需求和损伤指数,在结构损伤评估中不可忽略.

[1] SODERBERG E,JORDAN M.Seismic response of jumbo container cranes and design recommendations to limit damage and prevent collapse[C]∥Ports.2007:1-10.

[2] JORDAN M,ORITATSU Y,SODERBERG E.Seismic protection of quay cranes[C]∥Ports.2009:1-11.

[3] 王萌,石永久,王元清.强震作用下钢材等效本构模型应用研究[J].建筑结构学报,2013,34(10):84-92.

WANG M,SHI Y J,WANG Y Q.Application study on equivalent constitutive model of steel subjected to strong earthquake[J].Journal of Building Structures,2013,34(10):84-92.

[4] KOSBAB B D,JACOBS L D,DESROCHES R,et al.Analysis and testing of container cranes under earthquake loads[C]∥TCLEE 2009:Lifeline Earthquake Engineering in a Multihazard Environment 2009 ASCE.2009:842-852.

[5] JACOBS L D,DESROCHES R,LEON R T.Experimental determination of the seismic response of port container cranes including uplift phenomena[C]∥Structures 2009:Don’t Mess with Structural Engineers 2009 ASCE.2009:1632-1638.

[6] JACOBS L D,DESROCHES R,LEON R T.Experimental study of the seismic response of container cranes[C]∥Ports 2010:Don’t Mess with Structural Engineers 2010 ASCE.2010:91-99.

[7] KOSBAB B D,LEON R T,DESROCHES R.Seismic behavior considerations for jumbo container cranes[C]∥Structures 2009:Don’t Mess with Structural Engineers 2009 ASCE.2009:1000-1009.

[8] KOSBAB B D,DESROCHES R,LEON R T.Seismic behavior of a jumbo container crane including uplift[J].Earthquake Spectra,2011,27(3):745-773.

[9] JIN Y L,WU T X,LI Z G.Shaking table tests and numerical analysis for vertical seismic response of quayside container crane[J].International Journal of Structural Stability and Dynamics,2012,12(5):1-21.

[10] 郑培,张氢.大型集装箱起重机的抗震性能分析[J].武汉大学学报(工学版),2010,43(1):116-120.

ZHENG P,ZHANG Q.Analysis ofaseismic behavior of large scale container cranes[J].Engineering Journal of Wuhan University,2010,43(1):116-120.

[11] ZHENG P,ZHANG Q.Container cranes response predict on seismic load[C]∥11th International Conference on Parallel and Distributed Computing,Applications and Technologies,PDCAT.2010:504-508.

[12] 李哲,王贡献,王东.大型集装箱起重机地震动力学行为试验方法研究[J].武汉理工大学学报,2013,35(8):72-76.

LI Z,WANG G X,WANG D.Testing methods on dynamics behavior of jumbo container cranes under seismic loads[J].Journal of Wuhan University of Technology,2013,35(8):72-76.

[13] 李哲,胡吉全,王东.地震载荷作用下岸桥结构单参数畸变相似模型研究[J].振动与冲击,2014,33(20):164-169.

LI Z,HU J Q,WANG D.Distortion model of container cranes subjected to seismic load[J].Journal of Vibration and Shock,2014,33(20):164-169.

[14] GODA K,HONG H P,LEE C S.Probabilistic characteristics of seismic ductility demand of SDOF systems with Bouc-Wen hysteretic behavior[J].Journal of Earthquake Engineering,2009,13(5):600-622.

[15] 童根树,赵永峰.动力P-Δ效应对地震力调整系数的影响[J].浙江大学学报(工学版),2007,41(1):120-126.

TONG G S,ZHAO Y F.Dynamic P-Δ effects on seismic force modification factors[J].Journal of Zhejiang University(Engineering Science),2007,41(1):120-126.

[16] CHOPRA A K,GOEL R K.A modal pushover analysis procedure for estimating seismic demands for buildings[J].Earthquake Engineering and Structural Dynamics,2002,31(3):561-582.

[17] 余波,洪汉平,杨绿峰.非弹性体系地震动力响应分析的新型单轴Bouc-Wen模型[J].工程力学,2012,29(12):265-273.

YU B,HONG H P,YANG L F.Improved uniaxial Bouc-Wen model for seismic dynamic response analysis of inelastic system[J].Engineering Mechanics,2012,29(12):265-273.

[18] 建筑抗震设计规范：GB 50011—2010[S].北京:中国建筑工业出版社,2010.

Building seismic design specification：GB 50011—2010[S].Beijing:China Architecture & Building Press,2010.

[19] YI W J,YIN J.A new method for evaluating seismic performance based on displacement and energy[J].Journal of Hunan University,2009,36(8):61-67.