基于时延估计的麦克风阵列一致性分析
姚 欢,朱梦尧,朱晓强
(上海大学 通信与信息工程学院,上海 200444)
麦克风阵列是以特定方式排列,从而能够准确获取空间声场的一种拾音设备.基于麦克风阵列的典型应用涵盖现场录音、节目直播、会议通信、人机交互等领域.显然,性能优异的麦克风阵列技术及其解决方案为音乐、广播、电视、电影等文化产业发展提供了更多差异化的功能,必将得到广泛应用[1].
麦克风阵列信号处理的一个主要功能是估计源信号的位置.目前,基于麦克风阵列的声源定位方法大体上可分为3类: 1) 基于子空间的定位技术[2];2) 基于可控波束形成的定位技术[2];3) 基于到达时延差(Time Differences Of Arrival, TDOA)的定位技术[2].其中,基于到达时延差估计定位法计算量较小,硬件成本较低,定位精度较高,同时也易于实时实现,是目前声源定位法中常用的方法.TDOA方法首先求出声音到达不同位置麦克风的时延,再利用这些时延求得声音到达不同位置麦克风的距离差,最后用搜索或几何知识确定声源位置.目前已经出现了多种时延差估计算法,如广义互相关(Generalized Cross-Correlation, GCC)方法[3-4]、自适应最小均方方法[5]、基于空间的特征值分解方法[6]等.时延估计算法主要根据麦克风采集的信号进行定位,麦克风性能的好坏对后续数据的分析和处理影响极大,确保多路麦克风采集信号的一致性、有效性和保真性,是准确计算后续时延估计的关键.
然而,市场上麦克风仅给出频响范围、总谐波失真、信噪比、灵敏度等参数,受环境中温湿度影响,麦克风之间的参数波动不利于构造一致性高的麦克风阵列.目前,有通过标准传声器的参数对待校准传声器的参数进行校准的方式[7],选择高度一致性的麦克风对,但该方法仅适用于特定的麦克风,推广的成本高;有通过已知方位的校正源对阵列麦克风之间存在的幅度/相位响应误差进行校正,但该方法仅适用于高分辨率算法,不适用于时延估计算法[8-9];有自校正方法[10],无需设置校正源,可同时估计阵列误差和波达方向,但此类算法需要对阵列误差与波达方向进行联合迭代,或者需要对它们进行非线性多维寻优,因此计算量很大,在实际应用中具有较大限制.为此,本文提出一种新的麦克风一致性性能指标,选取满足一定指标值的麦克风对,即可实现对声源到达时延差的有效估计.本方法适用于时延估计算法,且计算量小,便于实际应用.本文建立了3组不同性能的麦克风阵列,且均可在实际环境中进行角度估计.通过对3组不同一致性性能指标的麦克风阵列进行角度估计结果分析,验证了此指标对麦克风阵列选型的指导意义.
1 时延估计算法
1.1 互相关时延估计
假设声场中只有一个声源,在无回声的开放空间里,语音源信号s(k)向外辐射传播,考虑只有两个麦克风,两个麦克风接收的信号y1(k)和y2(k)可表示为:
y1(k)=α1s(k-τ1)+n1(k),
(1)
y2(k)=α2s(k-τ2)+n2(k),
(2)
式中:α1,α2为由于传播效应导致的衰减因子,它的范围是0~1;s(k)为未知源信号;τ1,τ2为声源到麦克风1和2的时间延迟;n1(k),n2(k)为麦克风接收的加性噪声信号.
两个接收信号y1(k)和y2(k)之间的互相关函数定义为:
(3)
将式(1),(2)带入式(3),容易推导出:
(4)
若假设噪声信号n1(k)与源信号s(k)和另一麦克风接收的噪声信号n2(k)都不相关,式(4)可表示为:
(5)
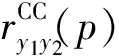
(6)
1.2 相位变换广义互相关算法(PHAT-GCC)
在会议环境中,不可避免的混响和噪声使得相关函数的最大值被弱化,甚至出现伪峰,造成角度误判.1976年Knapp和Cater提出了广义互相关(GCC)算法[3],其表达式为:
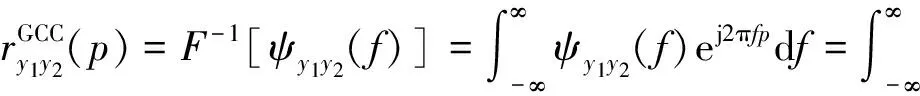
(7)
式中:F-1[·]表示离散时间傅里叶逆变换(Inverse Discrete-Time Fourier Transform, IDTFT);
(8)
为信号的互功率谱,且
(9)
ϑ(f)为频域加权函数.
由式(9)可以看出,TDOA的估计信息是通过互功率谱的相位而不是幅度来表示的.因此采用舍弃幅度保留相位的的加权函数

(10)
得到相位变换(Phase Transform, PHAT)[11]方法,此时广义互功率谱为
(11)
将式(11)带入式(7),得理想GCC函数
(12)
再将式(12)带入式(6),即可得到无混响且一定噪声强度下两个麦克风之间的时延
(13)
1.3 时延指标分析
上述的广义互相关算法中,角度估计的结果完全取决于时延估计的准确性,而时延估计的计算完全根据麦克风采集的信号进行,故麦克风采集信号的一致性、有效性和保真性对结果有直接影响.实际应用中,麦克风在不同温湿度条件下性能的差异,在基于麦克风阵列的广义互相关算法上主要表现为阵元之间估计时延差值与理想时延的差异.据此,本文提出一种新的时延误差指标,该指标建立在麦克风估计时延差值与理想时延的差异上,与麦克风之间的一致性相比,具有更广的适用性.
将上述广义互相关算法得出的估计时延值与理想时延值之间存在的误差,定义为时延误差Δτθk,表达式如下:

(14)

时延误差的均值表达式如下:
(15)
式中:n表示声源在角度θk时,一段语音帧内两两麦克风之间时延误差Δτθk的个数.
时延误差的方差表达式如下:

(16)
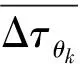
以两个麦克风为例,两麦克风的间距为6cm,声速取340m/s,根据声源到达两麦克风的时延差和声源与两个麦克风的几何关系,可得出时延差与声源角度的关系,如图1所示.
为方便后文表述,时延差与角度估计的几何关系,用F表示.

图1 时延差与角度估计的关系Fig.1 The relation between delay and angle estimation
角度估计的误差表达式为:

(17)

角度估计的方差表达式为:

(18)

据此,定义麦克风阵列一致性性能估计指标λθk:
λθk=-20lg(Δτθk/τθk).
(19)
理论上,在同一声源角度θk时,λθk的值越大,麦克风阵列估计的时延值越接近理想值,所估计的角度也越接近声源的真实值.
(20)
式中:N表示声源角度的个数.
2 实验验证
2.1 实验内容
为对比3组不同性能麦克风阵列在实际环境中单声源角度估计的性能,在一个大小为8m×7m×5m的会议室中进行实验.市面上的麦克风往往只提供频响范围、总谐波失真、信噪比等基本参数,如表1所示.

表1 3组麦克风阵列麦克风单元的基本参数
A组麦克风采用4个A单元作阵元,B组麦克风阵列采用4个B单元作阵元,C组麦克风阵列采用4个C单元作阵元.每组麦克风阵列上,阵元间距为6cm,一字排开,即每个阵列总长度为18cm.3组麦克风阵列实物图如图2所示.

图2 3组麦克风阵列实物图Fig.2 The picture of three sets of microphone arrays
在环境中选取点O作为麦克风阵列的中心点,将A组麦克风阵列的中心置于该点,麦克风阵列的4个麦克风阵元所在直线与房间的最长边平行.考虑到线性麦克风阵列的对称性,只需在麦克风阵列前左半平面放置声源,即可得到不同的角度及其时延差值.据此,选取了30°~90°内7个点(n1,n2,n3,n4,n5,n6,n7)作声源的放置点.
采用一段纯净的女声作为待估计的单声源信号,在以上7个点分别播放该语音30s,麦克风阵列以24kHz的采样率去采样声源信号,语音数据的帧长为1024个采样点,相邻两帧重叠为1/2.根据以上7个角度可得到两两麦克风不同的时延差值.
2.2 实验结果分析
将3组麦克风阵列采集的信号,根据相位变换的广义互相关算法,求出声源处于某点(以n6为例)时,相邻麦克风之间的时延估计值.将估计时延值与理想时延值做差,即时延误差Δτθk的结果进行对比,如图3所示.
从图3可以看出,相比于B组和C组麦克风阵列,A组麦克风的时延误差值接近于0的数目最多,说明实际应用中,有估计时延更为接近理想时延,不同差值的占有数目的发散程度处于3组中的中间水平.相比于A组和B组麦克风阵列,C组麦克风阵列的时延误差在某区间内具有3组中最多的数目,表现出最为集中的时延误差分布,说明实际应用中,其估计时延的稳定性更高.B组麦克风阵列的时延误差值为0的数目与A组相当,但有一个明显的次高峰,表现出大量的估计时延与理想时延有较大误差,时延误差的分布较为发散,说明实际应用中,容易出现较大的估计时延偏差,稳定性最差.
将每组麦克风阵列上相邻麦克风在各个角度上所有数目的时延误差取平均值(图4曲线中各点)及其方差(图4 曲线中各点上下线段),然后对3组麦克风进行对比,其结果如图4所示.
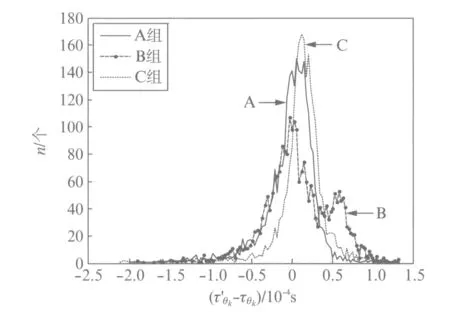
图3 3组麦克风阵列估计时延与理想时延的差值分布Fig.3 Estimation of delay and ideal delay difference distribution in three sets of microphone arrays

图4 3组麦克风阵列在各个角度上估计时延的误差Fig.4 Three sets of microphone arrays estimate the error of the delay at each angle
从图4可以看出,A组麦克风阵列的时延误差均值在90°时最低,越远离90°,时延误差均值越大.理论上,根据几何关系,理想的时延估计在90°最小,由广义互相关得出的时延估计也最小,故二者作差后,时延误差也相对偏小,A曲线基本符合理论依据.C组麦克风阵列表现出与A组类似的特性,而B组麦克风阵列,时延误差均值在各个角度基本持平,在时延估计时,出现了较大偏差,符合图3得出的结论.从图4还可以看出,相比于A组和B组麦克风阵列,C组麦克风阵列在各个角度上时延误差的方差最小,说明其角度估计上可能有更高的稳定性.
根据式(19)求取3组麦克风阵列在不同的角度上的估计时延误差一致性性能指标,计算结果如图5所示.
从图5可以看出,声源在90°时,性能指标最小,越远离90°,性能指标越高.因为在90°时,理想时延值接近为0,无论时延误差多小,都使得理想时延值与时延误差的比值趋向一个极小值,表现在性能指标上,就是取值极小.而在30°时,理想时延值为较大值,基于相位变换广义互相关算法计算的估计时延值与理想时延的偏差不会很大,使得理想时延值与时延误差的比值比较大,表现在性能指标上,就是取值较大.3组麦克风阵列的性能指标随角度的变化符合理论依据.在3组麦克风阵列中,A组麦克风阵列的平均性能指标最高,B组和C组在60°之后,C组的性能指标相对较高,而在60°之前,互有优劣.
根据广义互相关算法得出的时延估计,经过几何关系,可得到3组麦克风阵列在实际环境中的角度估计值.因声源角度已知,可得到3组麦克风阵列在各个角度上估计的方差,其结果如图6所示.

图5 3组麦克风阵列估计时延误差性能指标Fig.5 Error performance parameters of estimating delay of three sets of microphone arrays
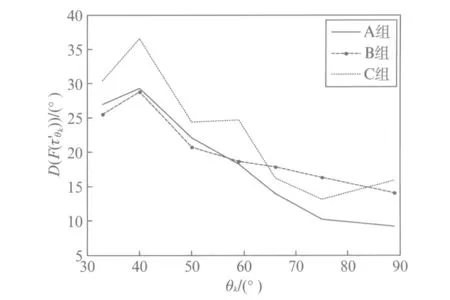
图6 3组麦克风阵列在各个角度上估计的方差Fig.6 The estimated variance of three sets of microphone arrays at each angle
从图6看出,声源在阵列前方90°方向时,A组麦克风阵列角度估计的方差最小,随着声源越来越偏离麦克风阵列中轴线,A组麦克风阵列的角度估计的方差逐渐增大.理论上,声源在阵列正前方时,麦克风之间的时延最小,互相关算法得出的估计时延误差小,对应的角度估计误差也小;而声源位置偏向麦克风阵列中轴线一侧后,麦克风采集的信号之间受多径和混响等因素的影响变大,进而互相关算法计算的估计时延出现偏差的范围变广,影响最终的角度估计.B组和C组麦克风阵列的角度估计的方差出现了与A组麦克风阵列类似的趋势,符合理论依据.比较3组麦克风阵列,可以看出A组麦克风阵列的角度估计性能最强,B组麦克风阵列在约为65°之前,其角度估计性能强于C组麦克风阵列,而在约65°之后,C组的角度估计性能略好于B组麦克风阵列.
对每一个角度,按公式(18)和(19)计算麦克风阵列角度估计的方差与一致性性能估计指标.以麦克风阵列一致性性能估计指标为横坐标,以角度估计的方差为纵坐标,将每组麦克风所得结果绘制成曲线.将每组麦克风的一致性性能指标按照公式(20)进行计算得出一致性平均性能指标,将结果标注于各条曲线上.3组麦克风的一致性性能估计指标与角度估计的方差的关系,其结果如图7所示.

图7 3组麦克风阵列性能指标与角度估计的方差的关系Fig.7 The relation between the performance indexes of three sets of microphone arrays and the variance of angle estimation
从图7可以看出,A组麦克风的性能指标越小,角度估计的方差也越小,性能指标增大,角度估计的方差也随之增大.结合图5,因不同角度有不同的理想时延和估计时延,在麦克风阵列正前方有较小的性能指标和估计时延,符合理论依据.B组和C组麦克风阵列性能指标与角度估计的方差之间的关系与A类似,不再赘述.
从图7中还可以看出,A组麦克风阵列时延误差的平均性能指标最高,相应地其麦克风阵列角度估计的方差最小,具有最好的角度估计性能.结果还表明,麦克风阵列一致性指标的平均值在14dB时,其角度估计的性能最好,而麦克风阵列一致性指标的平均值在10dB时,角度估计的方差明显差于14dB的情况.据此,根据麦克风阵列一致性指标的平均值筛选麦克风阵元,构造的麦克风阵列,具有良好的角度估计性能.
4 结 语
本文提出了一种新的麦克风一致性性能参考指标,构建了实际环境进行数据采集,搭建了3组不同性能的麦克风阵列,验证了该指标与角度估计的联系.为后续校正非理想指标值的麦克风阵列的研究提供了一种思路.实验结果表明,满足一定该指标值的麦克风阵列具有更准确更稳定的声源角度估计结果.因此,该指标的提出为麦克风阵列选型提供了指导意义.
[1] BENESTY J, CHEN J D, HUANG Y T. Microphone array signal processing [J].JournaloftheAcousticalSocietyofAmerica, 2009,125(6): 4096-4098.
[2] BRANDSTEIN M, WARD dr D.Microphone arrays [J].JournaloftheAcousticalSocietyofAmerica, 2002,112(3): 793.
[3] KNAPP C H, CARTER G C. The generalized correlation method for estimation of time delay [J].IEEETransAcoust,Speech,SignalProcess, 1976,24(4): 320-327.
[4] CARTER G C, NUTTALL A H, CABLE P G. The smoothed coherence transform(SCOT) [J].ProceedingsofIEEE, 1973,61(10): 1497-1498.
[5] REED F A, FEINTUCH P L, BERSHAD N J. Time delay estimation using the LMS adaptive filter-static behavior [J].IEEETransactionsonAcoustics,SpeechandSignalProcessing, 1981,29(3): 561-571.
[6] BENESTY J. Adaptive eigenvalue decomposition algorithm for passive acoustic source localization [J].JournaloftheAcousticSocietyofAmerica, 2000,107(1): 384-391.
[7] 王 利,王同庆.一种经济型测量传声器的改装、校准及应用 [J].航空动力学报,2010,25(9): 2041-2049.
[8] 王 敏,马晓川,鄢社锋,等.阵列幅度/相位误差的有源校正新方法 [J].信号处理,2015,31(11): 1389-1395.
[9] 贾永康,保 铮,吴 洹.一种阵列天线阵元位置、 幅度及相位误差的有源校正方法 [J].电子学报,1996,24(3): 47-52.
[10] 陈德莉,卢焕章,张 聪.空间非平稳噪声环境下阵列通道幅相误差自校正算法 [J].信号处理,2008,24(4): 525-529.
[11] CHERRY E C. Some experiments on the recognition of speech, with one and with two ears [J].JournaloftheAcousticalSocietyofAmerica,1953,25(5): 975-979.

