面向情感分析的古筝乐曲声谱图信息主干提取

肖仲喆，吴 迪，张晓俊，陶 智

(苏州大学 物理与光电·能源学部，苏州 215006)

古筝又名汉筝、秦筝、瑶筝、鸾筝等，是最古老的中国民族传统乐器中的一种，属于弹拨乐器，一弦一音.它的音色优美，音域宽广、演奏技巧丰富，表现力强,有“群声之主，众乐之师”之美称.战国时期盛行于“秦”地，最早为五弦，唐宋时为十三弦，后增至十六弦、十八弦、二十一弦等，目前最常用的规格为二十一弦.

古筝演奏是一门表演艺术，而有情感的演奏可以使音乐具有生命力、感染力，情感表现成为古筝演奏艺术的重要组成部分.作为一种表达情感及至入微的乐器，其演奏也是情感的产物[1-2].而古筝演奏中的情感表现作为非技术性因素，没有如演奏技法一般标准，与演奏者在演奏过程中对作品的理解有关，在同一作品中也有可能发生复杂的情感流动与变化.

在演奏者对古筝曲情感的表达中，在正确的控制音色、力度、速度，把握好旋律和节拍的变化的基础上，配合左手的按颤技巧，才能够表现出筝乐中的情感本质.左手恰到好处的“吟、揉、按、滑”在很大程度上决定了古筝演奏者的情感表达.例如，悲愤、恼怒的旋律，需要左手进行频率快、振幅大的猛颤，而优美如歌的旋律则需要左手颤音振幅小而均匀[3].

作为一种古老的传统民族乐器，在漫长的历史变迁中，古筝艺术与地域环境、文化、民俗等多种元素相结合，逐渐形成了多种不同的特色，很多筝曲，尤其是传统筝曲，会不同程度地受到古筝派别的影响,从地域上大致可以区分为南北两派.北派以河南筝和山东筝为代表，北派筝曲大多音色高亢豪放，粗旷明朗，左手按颤弦通常比较急且深，在旋律的处理上抑扬起伏较多；而南派的潮州筝曲、客家筝曲、浙江筝曲等，大多柔美含蓄，注重内在情感的抒发和表达，左手按揉弦变化比较多，风格偏于含蓄内敛，清秀淡雅，曲调上也比北派筝曲更加细腻婉约[4].

除左手的按、颤弦外，右手的触弦位置、力度，古筝演奏中特有的刮奏、摇指等技法的恰当运用，在古筝的情感表现中也起到重要作用.

在基于音频信号的古筝曲分析中，提取出不同表现技法在信号中的特征，是进行古筝乐曲情感表达的基础.对于乐曲情绪的分析，近年来已成为音乐信息提取中的一个重要方面之一[5-6].然而，基于机器学习算法的自动音乐情绪分析，首先依赖于对情绪的精确标注，常见的标注方法主要有使用离散的情绪种类或者维度空间，例如价效-激励二维空间[7].Saari等[8]对音乐情绪标注进行了详细的分析.然而，古筝作为一种中国传统乐器，尚未有专门针对此种乐器的乐曲进行了情绪标注的数据库，并且，常用于西方音乐情绪描述的类别，也并不适用于古筝曲，尤其是传统古筝曲.因而，对古筝乐曲的情绪分析，首先需要了解古筝各流派主要乐曲背景的专业人士进行标注.在目前缺少标注库的情况下，对古筝乐曲进行分析，对能够表现出情绪变化的演奏技法进行识别，则是对古筝曲情绪进行自动识别的基础.

声谱图作为同时体现声音信号的时域、频域特征的综合的可视化表达方式，能够保留声音信号中的大多数信息，因此能够将数字图像处理方法引入到音频信号分析中.声谱图相似度可被用于音乐检索[9-10]或音乐风格分析[11-12]；而将声谱图作为图像，通过对其图像二维频谱的分析，可以对语音和音乐信号之间进行分类[13]；多分辨率的声谱图也被用于伴奏音乐与歌唱人声的分离[14].虽然尚未见文献中提及使用声谱图进行音乐情绪的分析，但音乐情绪分析与音乐风格分析可以采用类似方法，因而本文将声谱图作为对筝乐分析的载体.

按、颤、触弦位置等都会引起声谱图纹理变化，而这些信息都属于声谱图中的局部细节信息，不易提取，若能先对声谱图进行主干信息分析，就可以在围绕声谱主干的基础上对各局部的细节信息进行分别提取.本文提出了一种基于有限峰值中心点的声谱图主干提取方法，作为后续研究中对古筝曲进行情感表现技法的细节分析的基础.

1 古筝简介

目前，最通常的古筝型号为S163-21，其中： S代表S形岳山，王巽之与缪金林共同发明；163代表古筝长度为163cm左右；21代表古筝弦数为21根.古筝正面图如图1所示[15].前梁、后梁也称前岳山、后岳山.

图1 古筝结构图Fig.1 Structure of Guzheng

古筝的21根弦为一弦一音，使用五声调式，最常用的调式为D调，以距离演奏者最近的弦为第1弦，对应的唱名为倍高音do，距离演奏者最远的弦为第21弦，对应的唱名为倍低音do.通常情况下，第3，8，13，18这4根弦采用绿色或红色进行标识，以方便演奏者在演奏中区分音区.可以采用十二平均律进行调音，弦号、音名、唱名、频率(保留整数)的对应关系列于表1.

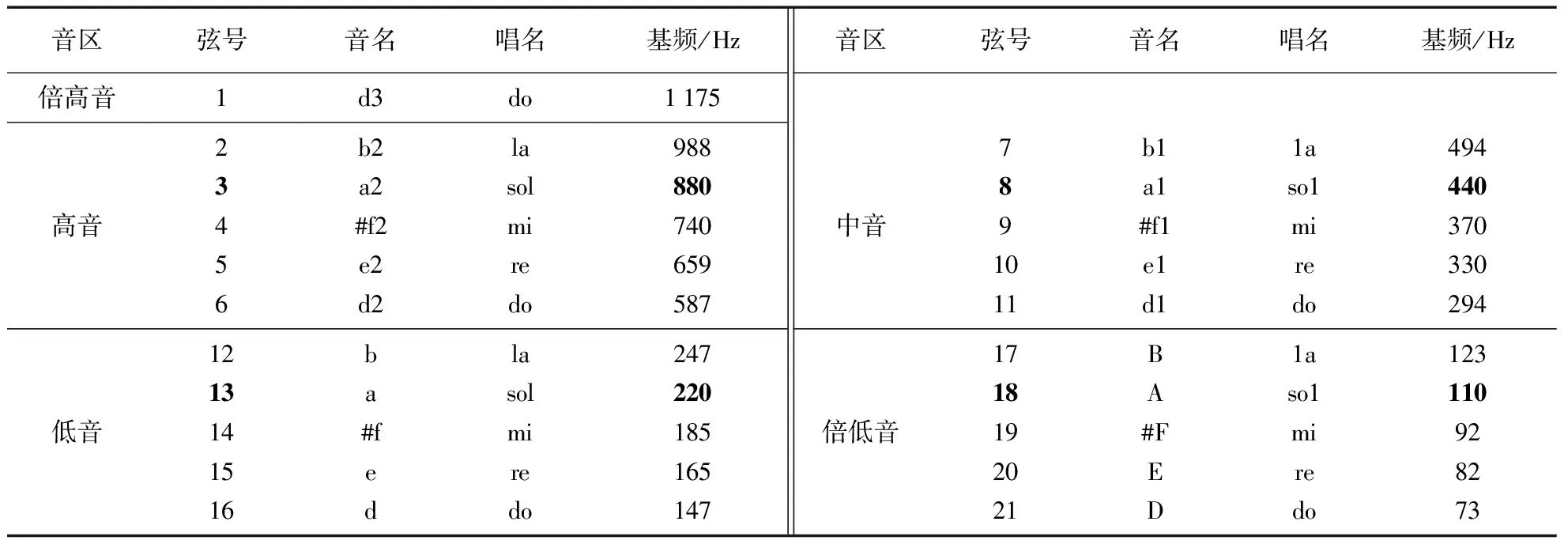
表1 古筝D调，各弦基频

注： 加黑的数据表示古筝上对应序号的弦采用绿色或者红色进行标识，以方便演奏者.

2 古筝常用指法的单音时频分析

古筝作为一种一弦一音的弹拨乐器，有其独特的音色特征，而不同的演奏技法则会引起音色的细微变化，从而有不同的表现力，同时也会在频谱、声谱图上体现出差异.

2.1 触弦位置对古筝单音频谱的影响

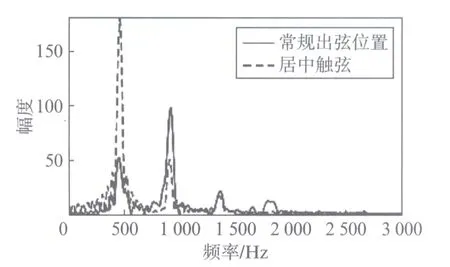
图2 触弦位置对频谱的影响Fig.2 Influence of position of contact point to spectrum

古筝右手触弦位置是直接关系到音色的表现.通常，初学者时右手的基本触弦位置是在距前岳山约3cm处，而基本音质的最佳触弦点，则是在发音弦段1/8处，即本音第3个八度的泛音位置，在这个位置上弹弦发音纯净响亮.在实际演奏中，演奏者会根据乐曲的需要，选择不同的触弦点以获得不同的音色，如明暗变化、刚柔变化等.触弦位置对频谱的影响如图2所示.

图2中所示两个音均为第8弦，标准基频为440Hz.实线所示的义甲触弦位置距前岳山约3cm，为常规触弦位置，虚线所示的触弦位置约为有效发声弦长的中点，常用于表现较轻、较柔和的音色.由图2可见，居中触弦时，基频分量的幅度较常规位置触弦时有了明显的提升，从而引起频谱的整体重心向低频方向转移，使音色变得更加厚重，音色不再明亮，从而显得更加柔和.

2.2 相同触弦位置在不同弦上的频谱变化

作为一种多弦乐器，古筝具有21根琴弦，跨越4个八度的范围，高音区与低音区的音色存在明显差异，而频谱特征也存在明显区别.本文选择D调唱名为sol的4根弦(从高音到倍低音，第3，8，13，18弦)进行分析，触弦位置均为距前岳山3～4cm处，琴弦进入稳定振动状态后某时刻的取长度为30ms的短时帧的频谱如图3(a)所示.由图3(a)可见，高音区和中音区(第3，第8弦)基频分量有明显的较高幅度，而低音、倍低音区的基频分量幅度显著降低.

为更清晰地显示高低音区的频谱差异，频率按照各弦的基频进行归一化，将横坐标转换为谐波，重绘于图3(b).由图3(b)可见，高音sol(第3弦)的基频分量明显为该音的最高频率分量；中音sol(第8弦)的2次谐波幅度已经接近基频分量幅度；低音sol(第13弦)的基频分量已不易辨别，第2、3次谐波幅度明显较高；而倍低音sol(第18弦)的基频分量几乎缺失，2次谐波分量也较低，最高幅度出现在4次谐波处.这一差异一方面是因为古筝琴弦音越低则有效弦长越长，相对于前岳山相同距离的触弦位置相对于弦长的比例就越小，相当于更接近前岳山进行触弦；另一方面由于古筝从第1弦到第21弦的直径差异很大，也会造成频谱特征的区别.

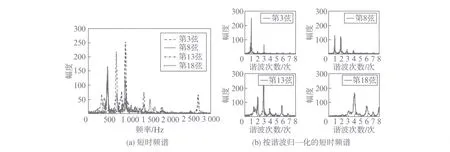
图3 第3，8，13，18弦在常规触弦位置的情况Fig.3 Short time spectrum of strings 3，8，13，18 at normal touching position

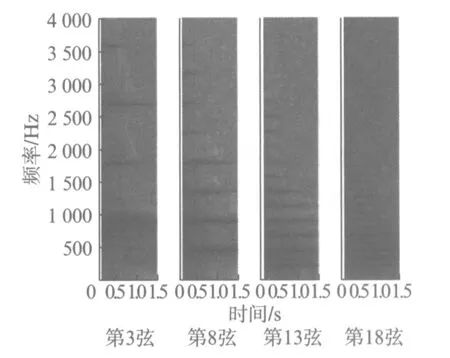
图4 第3，8，13，18弦的声谱图Fig.4 Spectrogram of strings 3，8，13，18

图4为上述各弦的声谱图.由图4可见与图3(b)类似的信息，第18弦基频分量在声谱图中不可分辨，发生了基音缺失.同时，各弦的声谱均表现出高频分量比低频分量衰减快的现象.

2.3 揉、颤弦对声谱图的影响

左手的揉、颤弦可以引起古筝琴音的基频在原有基础上发生波动，揉、颤的幅度、频率都可以在声谱图上造成变化，不同力度、频率的揉、颤弦，可以使声谱图中的条纹产生波动，造成或条纹变粗，或条纹边缘模糊等效果.而从听觉上，揉、颤弦可以使音色发生不同变化，同时可以产生延长发声的作用.以第8弦(基频440Hz)为例，无揉颤弦与有揉颤弦时的声谱图对比如图5所示.

由图5可见，当加入揉弦时，由于左手对弦施加变化的压力，造成弦上张力的变化，从而引起基频的波动，表现为声谱图中的条纹发生起伏变化.

2.4 滑音的声谱图特征

古筝演奏中，可以通过左手按弦产生滑音效果，例如，sol音可以通过按弦变化到#sol或la音.其中，上滑音为先弹响琴弦，一般在当前音符时值大约一半的时刻进行按弦，而下滑音为先按弦，弹响后在当前音符时值大约一半的时刻放开.滑音声谱图的例子如图6所示.

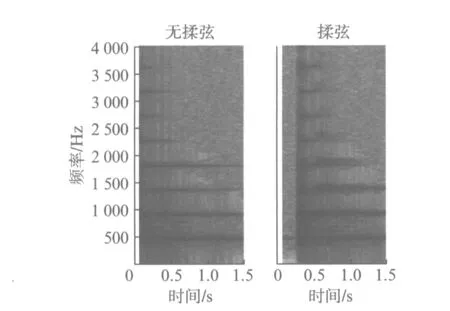
图5 第8弦，有无揉弦对声谱的影响Fig.5 Influence of vibrato to the spectrogram

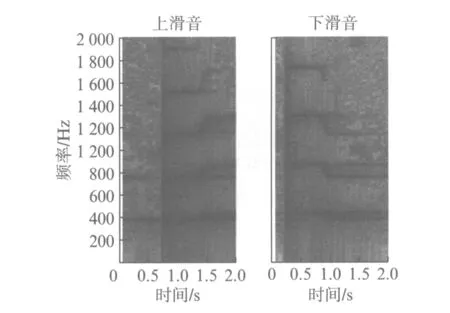
图6 上、下滑音的声谱图Fig.6 Spectrogram of portamento

由图6可见，在滑音的声谱图中，声谱条纹会在按弦或放弦时刻发生倾斜，最终在新的位置形成横条纹，而按弦或放弦时刻前的谐波频率处的横条纹会继续持续存在一段时间.

2.5 短时间内多次触弦技法的声谱图特征

古筝演奏技法中，刮奏、摇指等均为短时间内多次触弦的技法.古筝刮奏指连续划过相邻的若干根琴弦，分为上行刮奏与下行刮奏.由于刮奏过程中，相邻各弦间的触弦间隔时间短，且各相邻弦间的基频差距小，因此声谱图表现为较密集的条纹，且音头部分呈现明显的曲线，如图7(a)所示.上下行刮奏均出现了密集的横条纹，上行刮奏中可以明显看出从左下向右上的曲线，而下行刮奏中可以明显看出从左上向右下的曲线.

摇指为古筝中较有特色的指法，指以大指义甲在同一根弦上快速连续均匀的进行托劈交替的弹奏，使古筝的颗粒性的音效变化为连续声音，其声谱图也表现为若干条连续的横线条纹，但由于摇指过程中义甲频繁触弦，各次谐波分量均不会出现明显衰减.同时，由于触弦瞬间会产生谐波位置之外的杂音，因而有可能在非谐波位置处也有单次触弦时更高的能量出现.摇指声谱图如图7(b)所示，图中弹奏的琴弦为第8弦.

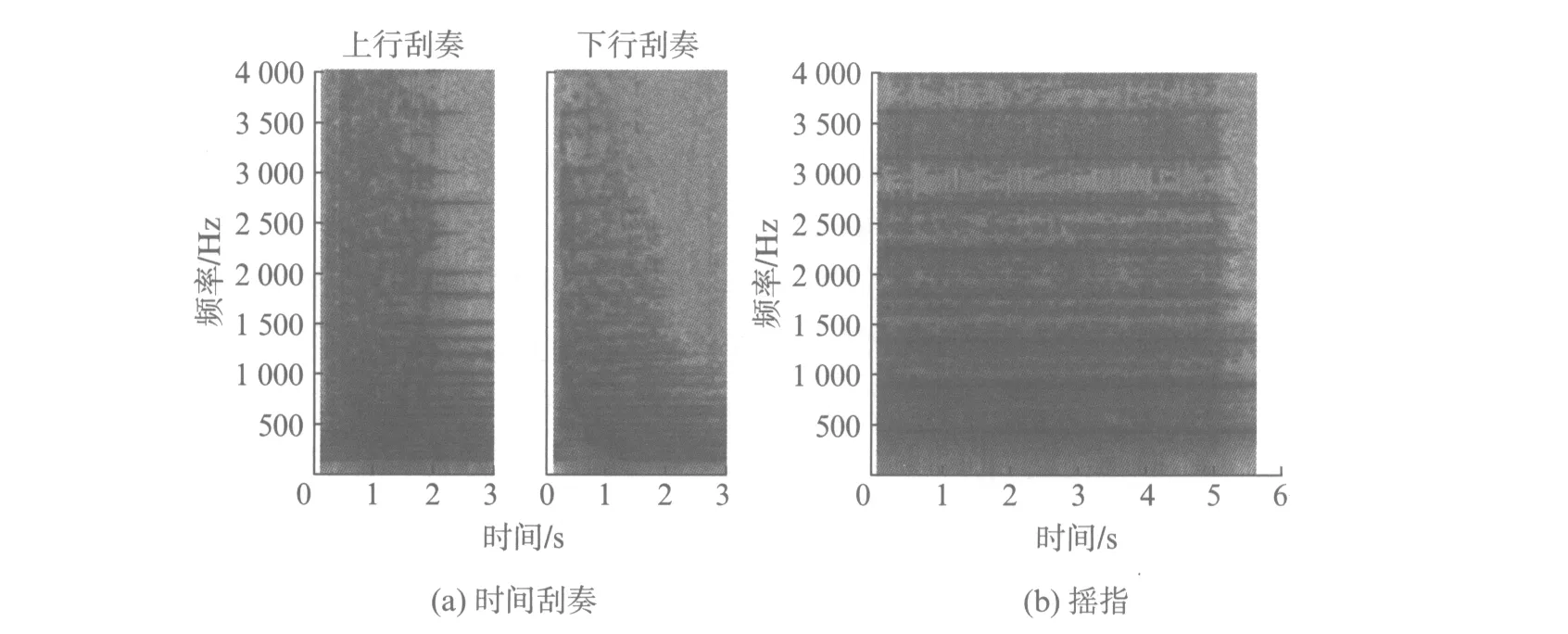
图7 多次触弦技法的声谱图Fig.7 Spectrogram in notes with multiple string touchings

2.6 泛音的声谱图

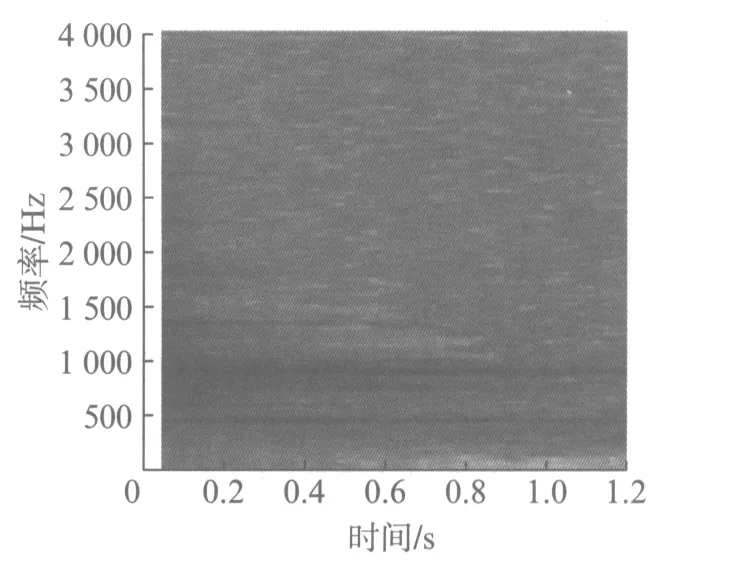
图8 泛音的声谱图Fig.8 Spectrogram of overtone

古筝的泛音弹奏方式为，在右手义甲触弦的瞬间，以左手指尖在当前琴弦的有效长度1/2处触弦并迅速离开，可以得到清脆明亮的音色，有时可用于模拟钟声等，其时域波形光滑，频谱由2次谐波占主导地位.泛音的声谱图如图8所示，其2次谐波位置的声谱图条纹颜色明显比其他条纹深，而基频与其他谐波较弱，与普通的弹奏方式产生的声谱图有明显差异.

3 基于声谱图的古筝乐信息主干提取

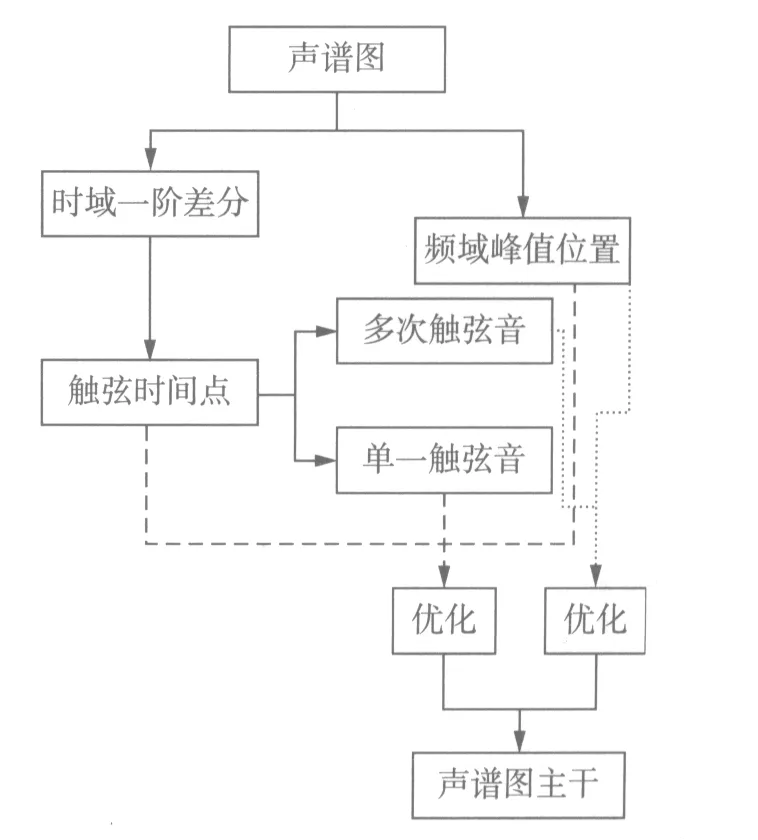
图9 声谱图主干信息提取流程图Fig.9 Diagram of spectrogram main trace extraction

由第2节的古筝主要指法的单音分析可知，古筝乐曲的声谱图主要表现为一系列在每个音的范围内随时间衰减的横条纹，并会由于揉、颤弦、滑音等在横条纹的附近发生细节变化，而刮奏、摇指等密集触弦的指法，则会产生如曲线形音头轨迹，密集条纹，或不随时间衰减等变化.揉、颤弦、滑音、刮奏、摇指等均为能够影响古筝演奏情感表达的重要因素.这些因素所产生的声谱图细节变化不易直接提取，因而本文通过一种基于有限峰值中心点的声谱图主干提取方法，获取声谱图条纹中心位置作为乐曲框架式的脉络，则可以作为分析基础，围绕各条纹中心线对声谱图的细节变化进行进一步的分析.

3.1 声谱图主干提取方法实验设计

声谱图的主干提取分为时域、频域两个方向分别进行，如图9所示.古筝演奏中，对一个音符的表现，分为单次触弦与多次触弦两类.其中，多数的普通技法均为单次触弦，而刮奏、摇指等技法则为短时间内均匀的多次触弦.

声谱图主干提取的第1步，通过对声谱图进行时域一阶差分，获取触弦时间点.通过是否出现短时间内的密集触弦点，判断该音符属于单一触弦技法或是多次触弦技法.第2步，根据频谱峰值位置，将声谱图转化为稀疏矩阵，并经过优化，获取声谱图主干.优化过程中，单一触弦音使用当前音符触弦激发后的能量较强的时间段的信息，而多次触弦音使用当前音符所占所有时间的信息.

3.2 时域主干提取： 触弦时间点提取

声谱图主干提取，首先需要进行触弦时间点的提取.对于单次触弦的音，触弦时间即为此音符的起始时间，而多次触弦的音，密集的连续触弦时间的第一次触弦即为此音符的起始时间.对触弦时间点的提取，可以进行各音符之间的分割，以及提取节奏等乐曲重要信息.

图10为《渔舟唱晚》(宋心馨演奏版本，乐曲下载于中国古筝网)的起始部分，仅包含单次触弦技法.图10(a)中灰色曲线为时域波形，横坐标为时间(s)，纵坐标为幅度；图10(b)为对应的声谱图，横坐标为时间(s)，与图10(a)对齐，纵坐标为频率(Hz)，只显示了0至2000Hz部分.由时域波形可以看到，触弦点的时域波形包络会有突发上升，然而，在一个音符时间范围内，时域波形包络衰减并非单调，例如图10(a)在0.6s附近有明显的上升；同时，此次的时域幅度高于6.9s附近第5个音符的触发幅度，因而，即便在时域波形包络上升位置处配合幅度的阈值判断仍不便进行触弦点的准确提取.

由图10(b)的声谱图可以看到，在每个音符的稳定振动状态下，声谱图表现为若干条平行的横条纹，而横条纹之间的幅度较低，但在触弦点处，由于触弦瞬间义甲与琴弦的碰撞，不可避免的会带来一定的触弦声，即便控制在不易听辨出的程度，依然可以在声谱图中看到每个触弦点处均有较明显的分布于各横条纹之间的峰值.对声谱图作时间方向的一阶差分，则可在各触弦点得到明显大于其他位置的数值，表现为纵向条纹.设被分析的音乐段的声谱图为S(n,k)，其中：n为离散信号的时间序号，n=1,2,…,N；k为对应的频率序号，k=1,2,…,K.其一阶差分结果为：

DT(n,k)=S(n+1,k)-S(n,k)n=1,2,…,N-1；k=1,2,…,K.

(1)

声谱图的一阶差分结果二值化后的结果如图10(c)所示，提取各纵条纹的时间位置，即为触弦时间点.经微调修正的触弦时间点以黑色竖线标记于图10(a)中.

当演奏中出现刮奏、摇指等短时间内多次触弦的演奏技法时，对触弦时间点的提取则会呈现密集结果，如图11(a)中点划线框内所示.然而，刮奏、摇指等技法由于演奏中的反复触弦，造成对弦的反复激发，在最后一次触弦时间之前，声音能量不会发生明显衰减，造成声谱整体能量较高，因而时域一阶差分结果虽然能够体现密集触弦的特性，但是并不能完全准确地检测出密集的所有触弦时间点，从而检测出的密集时间点无法体现出均匀分布特性.

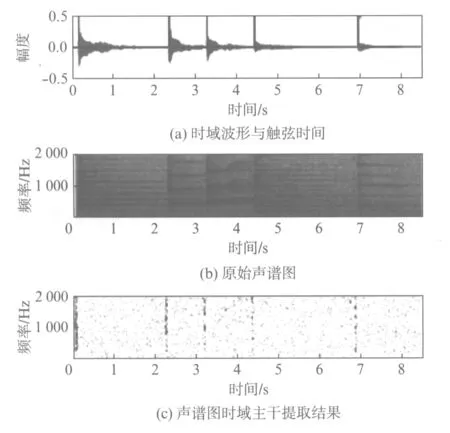
图10 渔舟唱晚片段Fig.10 A segment of “Yu Zhou Chang Wan”

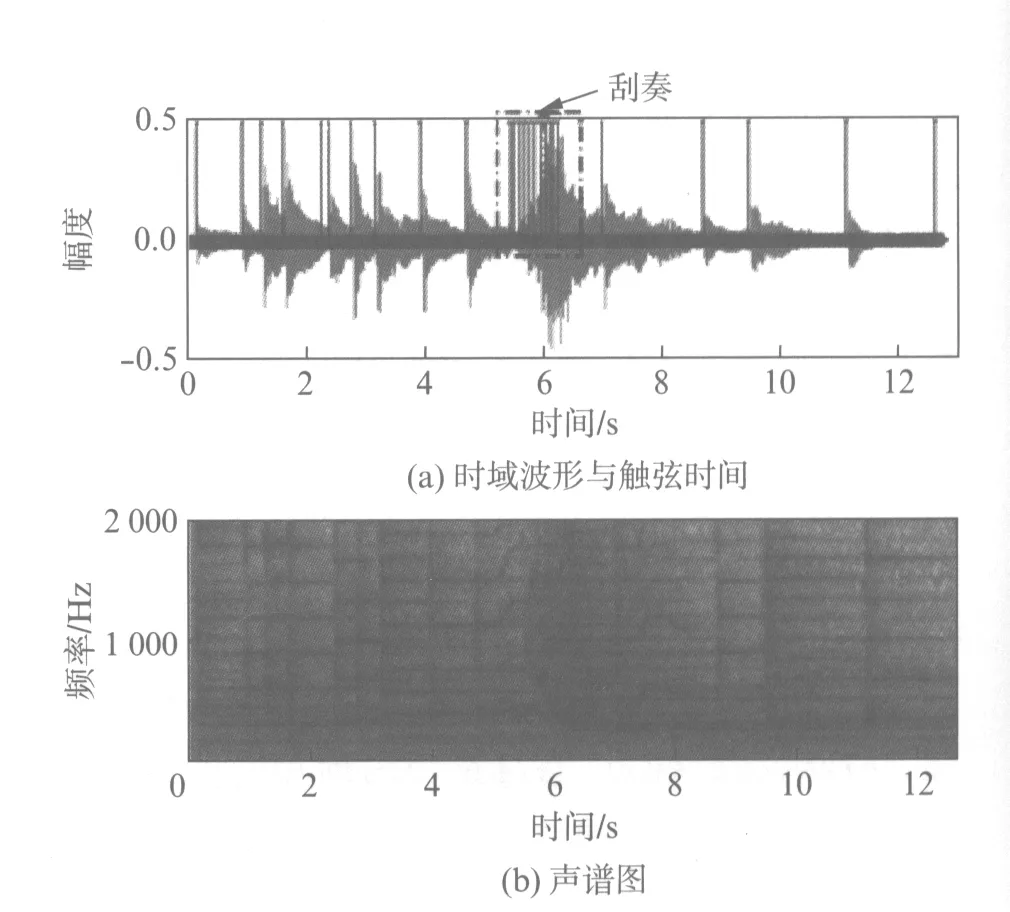
图11 含有多次触弦演奏技法的片段(渔舟唱晚)Fig.11 A segment with multiple string touchings(“Yu Zhou Chang Wan”)

3.3 频域主干提取： 各音符谐波频率提取

声谱图的信息内容为一个数据矩阵，每一个元素代表了它所在位置对应的时间、频率上的幅度值，其中包含的数据量较大，占用较大的存储空间，且不便于处理.孔旭等在研究声谱相似度的工作中提出了对声谱图的最大频率强度采样的方法[9]，即对每一帧存储其若干个幅度最大值的频率的坐标，并以各坐标构成识别特征矩阵.在古筝乐曲主干提取中，由于各次谐波的幅度关系会包含触弦位置等信息，因而最大幅值也需要被同时存储.本文提出了对声谱图进行两步频域主干的提取，其中： 第1步，将原始声谱图提取为稀疏矩阵；第2步，结合声谱图稀疏矩阵以及在时域主干提取中得到的触弦点时间，提取每个音符的最强的若干谐波，并将谐波显示在声谱图中各音符的起始位置处.

3.3.1 频域主干提取： 提取稀疏矩阵

此步骤的具体方法如下：

1) 对声谱图进行频域一阶差分，并对结果的符号再次进行频域一阶差分，结果中取值为-2的位置即为频谱峰值位置：

DF1(n,k)=S(n,k+1)-S(n,k)k=1,2,…,K-1，

(2)

DF2(n,k)=sign[DF1(n,k+1)]-sign[DF1(n,k)]k=1,2,…,K-2，

(3)

P=position(DF2(n,k)=-2)；

(4)

2) 对前一步获取的峰值位置所在处的幅值进行排序，保留前16位的坐标；

3) 保留提取出的16位坐标处的原始幅度数值，其余位置数据置0.

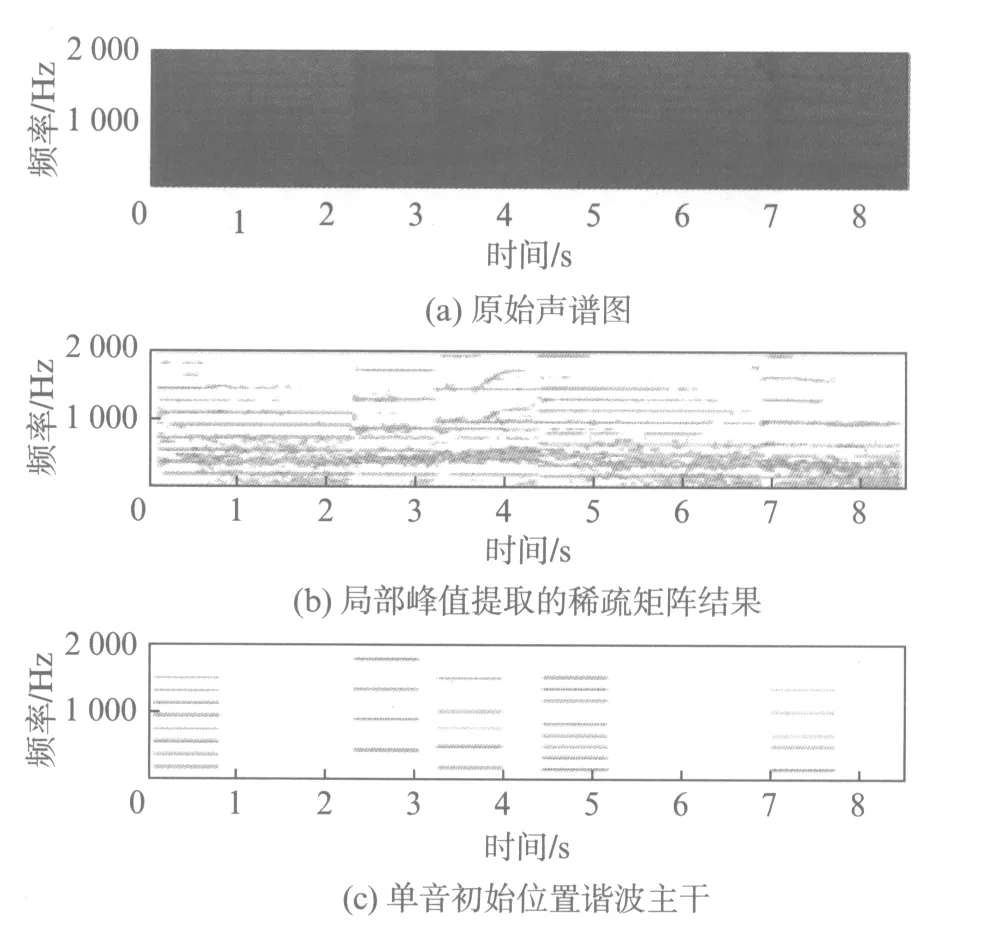
图12 渔舟唱晚片段Fig.12 A segment from “Yu Zhou Chang Wan”

经过此处理过程，每列数据从几千个数值化简为仅有16个非0值.图12为《渔舟唱晚》的初始片段，仅包含单次触弦技法，图12(a)为原始声谱图，图12(b)为处理后所得的稀疏矩阵.由图12(b)可以看到，声谱图中的主要条纹位置均得到了保留，然而，在主要条纹位置之外，存在若干散点，同时，在低频部分，存在前一音符的谐波条纹的延续，尤其以1000Hz以下部分更为明显，如第3s前后，第2个音符在0～2000Hz 内应有4个谐波存在，而另有4条对应于第1个音符的谐波条纹存在.

3.3.2 频域主干优化： 最强谐波位置提取

在将声谱图转化为稀疏矩阵的过程中，会残留若干不在谐波位置处的散点，且前一音符的部分谐波会持续存在，对后续音符产生影响.第二步的主要目的即为尽可能地去除散点，并删除来自于前一音符谐波位置的拖尾轨迹.具体方法为：

1) 对于单次触弦技法，以各触弦时间点为起点，选取至下一触弦时间点的间隔一半位置处，计算此时间区间各频率处在稀疏矩阵中有被保留元素的值的均值，并进行排序.对于多次触弦技法，选取密集触弦时间段内第一次触弦起至下一音符起始时间点的所有信息，计算各频率处在稀疏矩阵中有被保留元素的值的均值，并进行排序.

2) 设定谐波间隔阈值.由古筝最低音弦(第21弦)的基频约为73Hz，设定其频率值的一半，即：

thresf=36.5Hz

(5)

为谐波间隔阈值.

3) 根据步骤1)中排序后的被保留值，从最高值起，删除该音符时间范围内，稀疏矩阵中与其频率距离小于谐波间隔阈值thresf的所有点.

4) 对步骤3)中保留的频率值，取一阶差分，得到各保留频率间的间隔.当频率间隔均匀时，提取过程结束；当频率间隔不均匀时，分别提取奇数频率值间隔、偶数频率值间隔以及频率间隔的1/2值，连同所有频率点的间隔值一起，以上述所有间隔值中出现频次最高者作为该音符的实际谐波间隔，并标记出不符合本音符的谐波特性的频率值.

5) 对步骤4)中标记出的不符合本音符谐波特性的频率值，将出现在前一音符的谐波频率附近的值删除.

经过此处理过程，各音符位置平均会被保留4～8个谐波，如图12(c)所示.各音符的最强若干谐波被提取出来，仍存在部分音符有个别强度较弱的谐波被误删除，或前一音符的谐波拖尾未被识别的现象，但多数情况，前4个谐波可以得到准确的保留.此时，乐曲主干部分包含的信息包括：

i) 各音符的触弦时间点；

ii) 各音符的谐波频率值；

iii) 各谐波处的平均强度.

针对多次触弦技法的声谱图在频域主干提取时使用当前音符的所占的全部时值的信息，其结果如图13所示.其中，图13(b)为对摇指技法的声谱图进行频域有限数量峰值提取后的结果，由于摇指技法在演奏过程中需要快速频繁拨动同一根琴弦，在每次触弦过程中都会造成琴弦稳定振动模式的中断，因而提取出的结果也表现为不连贯的水平条纹，经平均优化后，获得如图13(c)所示的结果.图13(e)为对刮奏技法进行频域有限数量峰值提取后的结果，在其触弦时间段结束后，呈现密集水平条纹，而在其演奏起始阶段，即顺序拨动相邻若干根琴弦的过程中，呈现出圆弧状边缘.对此边缘进行提取后，如图13(f)所示.

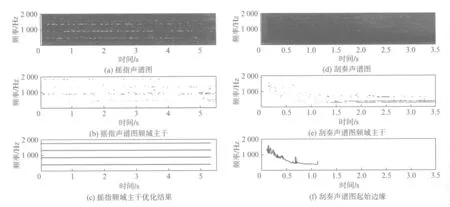
图13 多次触弦技法的声谱图的主干提取信息Fig.13 Key information extracted from notes with multiple string touchings

综上所述，可以通过对声谱图的分析，提取古筝单次或多次触弦演奏技法的声谱图主干信息.经过乐曲主干信息提取，相对于原始声谱图，可以大幅度地减少信息数据量，同时使乐曲特征更加清晰，便于进一步地深入分析.

4 结 语

本文根据相关文献中对古筝的演奏中的情感表达的研究，详细分析了对情感表达产生影响的各种不同演奏技法产生的声音信号在频谱以及声谱图方面的影响.另一方面，本文提出了一种基于有限峰值中心点的声谱图主干提取方法.这一由声谱图提取古筝乐曲主干的方法能够对乐曲中各音符进行分隔，并提取出各音符的前4～8个谐波位置与强度，能够作为后续对不同演奏技法引起的声谱图细节变化提取的基础，以便进行古筝乐曲情绪表达的分析.

[1] 李 莉.论古筝演奏中的情感表达 [J].大众文艺，2012(2)： 10-11.

[2] 王温豪.浅谈古筝演奏中的情感表现 [J].歌海，2008(4)： 67-68.

[3] 蔡丹丹.浅析古筝演奏中的情感表达 [J].音乐时空，2015(8)： 94.

[4] 石彬怡.浅析古筝演奏中的情感表达 [J].湖北科技学院学报，2014，34(5)： 125，129.

[5] HU X, DOWNIE J S, LAURIER C,etal. The 2007 MIREX audio mood classification task： Lessons learned [C]∥Proceedings International Conference on Music Information Retrieval. Drexel, USA： ICMIR，2008： 462-467.

[6] ALJANAKI A, YANG Y H, SOLEYMANI M. Emotion in music task at MediaEval 2014 [R]. Barcelona, Spain： MediaEval，2014.

[7] HU X, YANG Y H. Cross-dataset and cross-cultural music mood prediction： A case on western and Chinese pop songs [J].IEEETransactionsonAffectiveComputing，2016，PP(99)： 1. Doi： 10.1109/TAFFC.2016.2523503.

[8] SAARI P, FAZEKAS G, EEROLA T,etal.Genre-adaptive semantic computing and audio-based modelling for music mood annotation [J].IEEETransactionsonAffectiveComputing，2016，7(2)： 122-135.

[9] 孔 旭，关佶红.以声谱图相似度为度量的波形音乐检索 [J].计算机工程与应用，2009，45(13)： 136-141.

[10] 孔 旭.基于声谱图的音乐检索 [D].上海： 复旦大学，2009.

[11] CHOU C H, LIAO B J. Music genre classification by analyzing the subband spectrogram [C]∥2014 International Conference on Information Science, Electronics and Electrical Engineering. Washington, DC, USA： IEEE Computer Society，2014： 1677-1680.

[12] COSTA Y M G, OLIVEIRA L S, KOERICB A L,etal.Music genre recognition using spectrograms [C]∥The 18th International Conference on Systems, Signals and Image Processing. Washington, DC, USA： IEEE Computer Society，2011： 1-4.

[13] NEAMMALAI P, PHIMOLTARES S, LURSINSAP C.Speech and music classification using hybrid form of spectrogram and Fourier transformation [C]∥2014 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference. Washington, DC, USA： IEEE Computer Society，2014： 1-6.

[14] TACHIBANA H, ONO N, SAGAYAMA S.Singing voice enhancement in monaural music signals based on two-stage harmonic/percussive sound separation on multiple resolution spectrograms [J].IEEE/ACMTransactionsonAudio,Speech,andLanguageProcessing，2014，22(1)： 228-237.

[15] 沪江部落网友.第二期 基础知识(二) [EB/OL].http：∥bulo.hujiang.com/menu/109899/item/830251/.