吸力步长和加载时间对土水特征曲线测试结果的影响规律和修正方法

伊盼盼，牛圣宽

(1. 武昌理工学院，武汉 430023；2. 长江勘测规划设计研究有限责任公司，武汉 430010

0 引 言

非饱和土的土水特征曲线描述基质吸力与饱和度之间的关系，在分析非饱和土的变形及强度问题、污染物地下迁移等问题时起着重要作用[1-4]。

传统的室内测试非饱和土土水特征曲线常用的仪器为压力板仪[5]，其原理为每施加一级压力后试样达到平衡状态再施加下一级吸力。这种方法耗时较长(粉土约一月，粉质黏土约两月)，在吸力较高的情况下，试样底部与陶土板贴合较差并且在陶土板的背面的橡胶膜上积水，这些现象会影响试验精度。

近来提出的关于快速测定非饱和土土水特征曲线的方法的有一步流动方法[6]和动态多步流动方法[7]。一步流动方法是初始对试样施加一小吸力(进气值左右)，待试样达到平衡时，再施加一较大吸力值直至试样达到平衡状态，得到溢出水量随时间的变化关系，然后根据VG模型[8]拟合得到试样的土水特征曲线。该方法由于仅施加一步吸力，故试验时间较短，但是在根据VG模型拟合时存在参数不唯一的现象，对试验结果造成一定影响。Smiles等[9-11]对土水特征曲线的唯一性进行了研究，发现试样在平衡时的含水量不但与吸力值有关，而且与施加基质吸力的步长及时间有关，这种现象被称为“动效应”。Wildenschild等[12]也发现了这种“动效应”，并从进气值、动态接触角等方面解释了产生该“动效应”的原因。Hassanizadeh等[13]基于热动力学多孔介质理论，提出了一个能够描述非平衡流动过程的动态模型。

Wei & Dewoolkar等[14,15]指出可以把这种基质吸力和饱和度随时间变化率值的线形相关性用于模拟非平衡态的多步流动试验结果。动态多步流动方法是在此基础上提出的。该方法的思路是：建立非平衡条件下非饱和土饱和度演化方程；接着开展动态多步流动试验；根据试验结果求解饱和度演化方程；根据容水率的定义确定平衡状态下试样的土水特征曲线。该方法中施加的吸力步数较多，由于每级吸力在上级吸力还没达到平衡状态时施加，可以节省试验时间，但是在该试验中不同的吸力步长和加载时间对试验结果有一定的影响，本文主要研究不同基质吸力步长和加载时间对多步流动试验结果的影响及如何确定合理的吸力步长及加载时间。

1 动态多步流动方法的原理

考虑一圆柱形非饱和土样，初始时，土样处于静力平衡状态，其饱和度为S0r，吸力为p0c=peq(c)(S0r)。若改变试样两端的压力差，试样中的水会从一端流向另外一端，故试样的孔隙含水量也会随之发生变化。基质吸力的变化与饱和度之间存在以下关系[7]：

这里，C是土水特征曲线Sr(pc)的斜率，也称容水率。

(1)

这里，C是土水特征曲线Sr(pc)的斜率，也称容水率。τ为特征时间。

图1 Ci～pic关系曲线Fig.1 The Ci～pic characteristic curve

根据每级吸力下实测的饱和度随时间的变化关系利用最小二乘法依次求得不同吸力步pic下的Ci值，从而建立Ci～pic的关系，如图1所示。根据C的定义，试样在pic吸力步下达到平衡时，其饱和度Sir与吸力pic之间的关系(即稳定状态下的土水特征曲线)近似于图1中的图形面积加上初始饱和度S0r。

对于非饱和土而言，基质吸力与饱和度间存在如下函数关系：

Pc=f(Seqr)

(2)

假设试样在基质吸力为P0c的作用下达到平衡状态时，此时试样的饱和度为Seqr0，即：

P0c=f(Seqr0)

(3)

然后，在吸力P0c的基础上给试样增加一个微小增量ΔP1c，使吸力达到P1c。当试样在P1c下达到平衡状态时，对应的饱和度的变化可以表示成：

Seqr1=Seqr0+ΔS1r

(4)

此时吸力与饱和度的关系为：

P1c=f(Seqr1)

(5)

将式(5)在Seqr=Seqr1处进行泰勒展开，ΔP1c是一个微小增量，因此，可以略去高阶项，式(5)可写成：

(6)

由上式可以得到试样在基质吸力P1c作用下达到平衡状态对应的饱和度Seqr1，其表达式为：

Seqr1=Seqr0+C1Δp1c

(7)

同理，当施加的吸力步为多步时，同样可以求得试样在基质吸力Pic作用下达到平衡状态对应的饱和度，其表达式为：

(8)

2 试验设备和试验方法

采用联合测试系统开展动态多步流动试验，其原理图如图2所示。

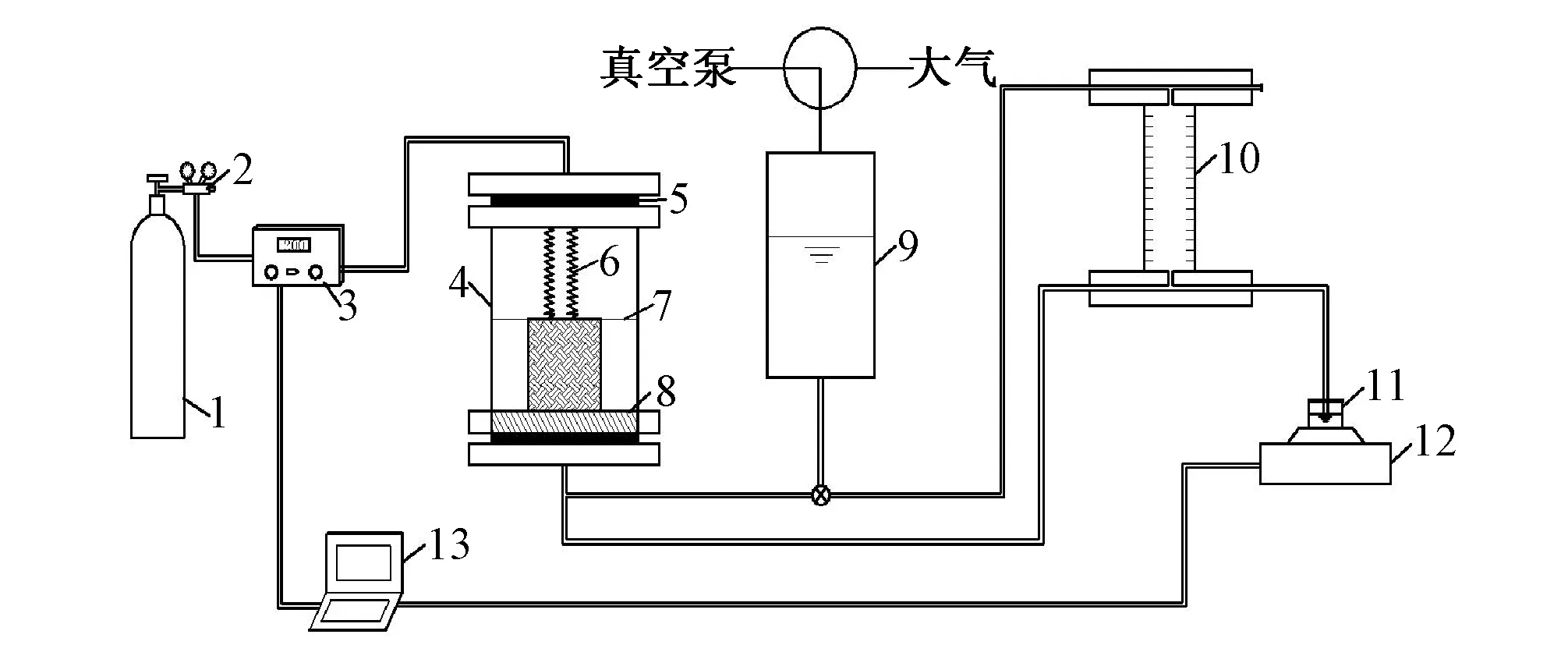
1-高压氮气瓶；2-减压阀；3-压力调节泵；4-压力室；5-密封圈；6-弹簧；7-铁丝网；8-高进气值陶土板；9-储水容器；10-气泡测量系统；11-盛水杯；12-电子天平；13-数据采集装置图2 联合测试系统示意图Fig.2 The sketch map of combined testing system

首先，制备试样。取重塑土样过2mm筛，然后测定土样的比重。根据试验设计的干密度配制土样，将制备好的试样和试验中选用的陶土板进行饱和。

在t0时刻，对试样施加第一级吸力增量Δp1c，直至t1时刻(此时试样并没有达到平衡状态)。接着，在t1时刻，施加第二级吸力增量Δp2c，保持吸力不变至t2时刻。根据类似的步骤，施加第n级吸力增量Δpnc，直至tn时刻，并推算出每级吸力步下饱和度随时间的演化关系。根据这组多步流动试验数据，利用最小二乘法可以推算出每级吸力下的容水率C，进而得到试样平衡态的土水特征曲线。

3 吸力步长和加载时间对试验结果影响分析

3.1 粉土动态多步流动试验结果分析

试验所用土样为取自黄河三角洲的粉土，其基本物理特性如表1所示。

表1 粉土基本物理性质Tab.1 Physical properties of the soil used in the test

根据预制干密度制备试样，对试样开展了三种不同的动态多步流动试验，施加的吸力步、相应加载时间和溢出水量随时间的变化曲线如图3所示。

图3 各动态试验施加的吸力步长及加载历时Fig.3 The suction step and the loading time duration of each dynamic test

从图2中可以看出，动态试验1和动态试验2施加的吸力步相同，共施加了9步吸力，施加的基质吸力历程为： 0～20～30～40～60～90～130～170～210～290 kPa，动态试验1在各吸力下的加载时间约8 h，共计68 h。动态试验2在各吸力下的加载时间约12 h，共计124 h；动态试验3施加了8步吸力，施加的吸力历程为：0～20～30～40～50～80～130～200～290 kPa，共计54 h。其加载历时相对前两种动态试验要短。为了进行对比分析，对该试样用压力板仪做了试样平衡条件下的土水特征曲线，历时17 d。

从图3中可以看出溢出水量随时间的变化关系，动态试验1和动态试验2施加的吸力步相同，各吸力步下的加载时间不同，试样的溢出水总量不同，但溢出水量随时间的变化曲线形状相近。动态试验3与前两种试验施加的吸力步相近，但加载时间较短，得到的溢出水流量曲线形状与前两种动态试验差别较大。

图3也表明了基质吸力增加越快，残余含水量越大的现象这是由于在排水的过程中会引起有一部分孔隙中的水被包裹而在其四周形成排水通路的现象，排水速率越大，这种现象越明显，导致试样的残余含水量也越大。

把溢出水量随时间的变化关系，换算成饱和度随时间的变化关系，利用前面提出的饱和度演化关系，并采用最小二乘法求出每级吸力下对应的C值，进而得出试样平衡态的水特特征曲线。以上三种动态试验得出的试样平衡态下的土水特征曲线如图4所示。

图4 各动态试验得到的SWCC曲线与实测曲线的对比Fig.4 Comparison of SWCC curves between measured curves and obtained by dynamic tests

动态试验1和动态试验2施加的吸力步相同，但加载时间不同。动态试验1在前两级吸力的加载时间和动态试验2相同，后面几级吸力的加载时间比动态试验2要短。从图4中可以看出，这两种动态试验得到的土水特征曲线和实测值比较接近，在饱和度较大时均与实测值基本重合，在饱和度较小时动态试验2的结果更加接近实测值。因此，从试验精度来看，这两种动态试验结果都可以满足试验要求。

动态试验3比前两种试验少加了一步吸力，但每级吸力的加载时间都比前两种试验的时间要短，图中所示动态试验3得到的土水特征曲线饱和度较大时与实测值比较接近，而饱和度较小时则与实测值有一定偏差，这主要是由于吸力值较小时，加载时间较短，使后面几级得到的土水特征曲线点向左偏移。因此前面几级的加载时间对后面的结果影响较大，应适当增加前面几级的加载时间，6～8 h为宜。

因此，对于粉土，在进行动态多步流动试验时，施加的吸力范围宜在10～300 kPa范围内；施加8～10级吸力步数即可满足试验精度，前4级步长的间隔应小一些，间隔控制在10～20 kPa之间为宜，每级的加载时间约6～8小时。后几级吸力可使间隔逐级增大，间隔控制在30～60 kPa之间为宜，每级的加载时间可控制在10～12 h；采用进气值为300 kPa的陶土板可满足实验要求。

3.2 粉质黏土动态多步流动试验结果分析

粉质黏土试样的基本物理性质见表2。

表2 粉质黏土基本物理性质Tab.2 Physical properties of the soil used in the test

由于测试系统的限制，其测试的范围仅在500kPa之内，难以得到较高吸力范围试样的土水特征曲线。因此，对于较高吸力范围的土样我们提出了一种修正的方法，即利用VG模型拟合动态多步流动方法测得试样在小吸力范围(500 kPa)内的土水特征曲线点，进而推算出试样在高吸力范围的土水特征曲线。

图5 各动态试验施加的吸力步长及加载历时Fig.5 The suction step and the loading time duration of each dynamic test

根据预制的干密度制备试样，对该试样开展了吸力步相同，加载时间不同的动态试验。施加的吸力步、相应加载时间和溢出水量随时间的变化关系如图5所示。

从图5中可以看出，这两种动态试验都施加了11步吸力，施加的基质吸力历程为： 0～10～20～30～40～60～90～120～160～200～240～290 kPa；这两种动态试验前五级吸力的加载时间相同，从第六级开始，动态试验2的加载时间开始减少。动态试验1的加载时间共计110 h，动态试验2的加载时间共计66 h，为了进行对比分析，对该试样用压力板仪开展了平衡条件下的土水特征曲线测试，历时65 d。

这两种动态试验得到的溢出水量随时间的变化关系如图5中的下图所示。从图5中可以看出，由于前几级这两种动态试验施加的吸力步和加载时间相同，得到的溢出水曲线也基本重合；从第六级加开始，由于动态试验2的加载时间比动态试验1的时间要少，其溢出水量也相应减少。由此可见，基质吸力步长变化越快，试样中的残余含水量也相应增加。

根据前面的求解方法，得出试样平衡态的土水特特征曲线。由于这两种动态试验仅测到吸力为290 kPa以内的土水特征曲线，这里，我们用VG模型对动态试验得到的土水特征曲线点进行拟合，得到相关的模型参数，把动态试验得到的土水特征曲线进行外推，进而得到高吸力范围的土水特征曲线。得到的模型参数如表3所示。

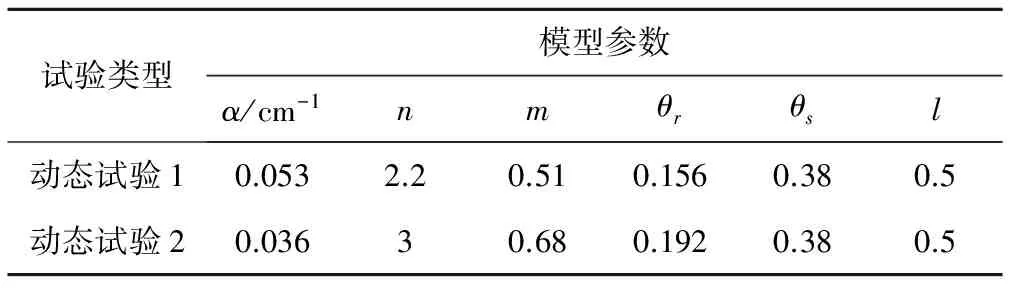
表3 试样的拟合参数Tab.3 The fitting parameters

动态试验得到的土水特征曲线和VG模型的拟合结果如图6所示。

图6 各动态试验得到的SWCC曲线及拟合曲线与实测曲线的对比Fig.6 Comparison of SWCC curves between measured curves and obtained by dynamic tests

为了进行对比分析，由压力板仪实测的试样土水特征曲线也在图6绘出。从图6中可以看出，动态试验1得到的土水特征曲线点和压力板仪实测的土水特征曲线点接近，且用VG模型外推得到的土水特征曲线基本通过实测点。这样既克服了联合测试系统中陶土板进气值的局限，又节省了试验时间。而动态试验2由于后面几级的加载时间较短，得到的土水特征曲线点与实测值偏差较大，VG模型外推的结果也不理想，因此，对于粉质黏土，各吸力步的加载时间应不低于10 m。

因此，对于粉质黏土，施加的吸力宜控制在10～500 kPa范围内，施加的基质吸力步数控制在9～10之间即可满足试验精度，前5级施加吸力的间隔应小一些，以10～40 kPa为宜，每级的加载时间不小于8～10 h，后几级吸力可使间隔逐级增大，以50～80 kPa为宜，每级的加载时间不小于10～12 h。

4 结 语

(1)动态多步流动试验测试土水特征曲线能大量节省试验时间，但是施加的吸力步数和加载时间对试验结果有一定影响。

(2)对粉土开展动态多步流动试验时，施加8～10级吸力步数即可满足试验精度，前4级间隔控制在10～20 kPa之间为宜，各级的载时间约6～8 h。后几级吸力间隔控制在30～60 kPa之间为宜，每级的加载时间可控制在10～12 h。

(3)对粉质黏土开展动态多步流动试验时，施加的基质吸力步数控制在9～10之间即可满足试验精度，前5级施加吸力的间隔以10～40 kPa为宜，每级的加载时间不小于8～10 h，后几级吸力可间隔以50～80 kPa为宜，每级的加载时间不小于10～12 h。

(4)对于粉质黏土试样开展动态多步流动方法测试500 kPa以内的土水特征曲线，利用VG模型拟合外推得出该试样高吸力范围土水特征曲线的方法是可行的。

□

[1] 李爱国，岳中琦，谭国焕等.野外土-水特征及其 工程意义[J].岩石力学与工程学报, 2004,23(6):969-973.

[2] 刘汉乐，周启友，徐 速.非饱和带中非均质条件下LNAPL运移与分布特性实验研究[J].水文地质工程地质，2006,(5):52-57.

[3] Fredlund DG, Equations for the soil-water characteristic curve [J]. Canadian Geotechnical Journal, 2011,31(4):521-530.

[4] Fredlund DG，AXing A，S Huang,Predicting the permeability function for unsaturated soils using the soil-water characteristic curve[J]. International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts, 2011,31(4):533-54.

[5] 孙树国，陈正汉，朱元青，等.压力板仪配套及SWCC试验的若干问题探讨[J].后勤工程学院学报，2006,(4):1-5.

[6] 伊盼盼,韦昌富,陈 盼,等.测定非饱和土水力参数的一步流动方法研究[J].岩土力学, 2012,(4):1 025-1 030.

[7] 伊盼盼,牛圣宽,韦昌富,等. 基于动态多步流动法的非饱和土水力特性测试研究[J]. 岩土工程学报,2016,(10):1 797-1 801.

[8] van Genuchten M T, A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils[J]. Soil Science Society of America Journal, 1980,44:892-898.

[9] Vachaud G, Vauelin M, Wakil M. A study of the uniqueness of the soil moisture characteristic during desorption by vertical drainage.[J]. Soil Science Society of America Journal, 1971,36(3):531-532.

[10] Toppg C, Klute A, Peters D B. Comparison of water Content-Pressure head data obtained by equilibrium, Steady-State, and Unsteady-State methods.[J]. Soil Science Society of America Journal, 1966,31(3):312-314.

[11] Smiles D, Vaehaud G, Vaulin M. A test of the uniqueness of the soil moisture characteristic during transient, nonhysteretic flow of water in a rigid soil.[J]. Soil Science Society of America Journal, 1971,35(4):534-539.

[12] Wildenschild D, Hopmans J W, Simunek J. Flow rate dependence of soil hydraulic characteristics.[J]. Soil Science Society of America Journal, 2001(65):35-48.

[13] Hassanizadeh S M, Gray W G. Thermodynamic basis of capillary pressure in porous media.[J]. Water Resources Research, 1993,29(10):3 389-3 405.

[14] Wei C F, Dewolkar M M. Formulation of capillary hysteresis with internal state variables[J]. Water Resources Research, 2006, 42,W07405:1-16.

[15] Wei C F, Muraleetharan K K. Linear viscoelastic behavior of porous media with non-uniform saturation. International Journal of Engineering Science.45: 698-715.