改进的入侵杂草优化算法在泰斯模型中的应用

邱云翔，刘国东，王 亮，李世钰

(1.四川大学 水利水电学院，成都 610065；2.四川大学 水力学与山区河流开发保护国家重点实验室，成都 610065)

0 引 言

在地下水资源开发利用的过程中，导水系数T和贮水系数S等水文地质参数是非常重要的基础数据。为获得符合实际情况的T和S，需对非稳定流抽水试验数据进行分析。常用的分析方法有配线法和直线图解法。数学模型的优化方法因其能高效模拟配线分析和Theis求解也成为反演T和S的分析方法，主要有高斯—牛顿迭代算法[1]，非线性最小二乘法[2]，遗传算法(GA)[3]，梯度法[4]，粒子群算法(PSO)[5]，GA优化BP神经网络法[6]等。上述方法均能反演出满足一定精度要求的T和S，但对T和S的初始取值范围取较大区间的情形研究较少。2006年，伊朗德黑兰大学的C Lucas和A R Mehrabian首次提出入侵杂草优化算法(Invasive Weed Optimization,IWO)[7]，该算法具备广度搜索的优势，目前已被应用于函数优化，模式识别，自动控制，数据挖掘，决策分析等诸多领域[8-10]。基于此，本文对IWO算法作适当改进，探讨其在T和S的初始取值范围取较大区间时反演T和S的有效性与稳定性。

1 IWO算法

IWO算法的实现步骤如下[7,8]：

(1)确定初始种群大小N0、最大迭代次数itmax、问题的求解维数dim、最大种群数量pmax、最大种子数zmax、最小种子数zmin、非线性调制指数n、初始标准差σinitial、最终标准差σfinal、自变量初始搜索空间xini，根据N0、dim、xini随机产生初始解。

(2)依据适应度函数计算初始解(父代种群)的适应度值，确定父代种群的最优适应度值和最劣适应度值。

(3)在具备初始解(父代种群)的基础上依据其适应度值计算繁殖种子的数量，种子数量与其适应度值呈线性关系，适应度值最优个体繁殖出zmax个种子，适应度值最劣个体繁殖出zmin个种子。

(4)父代种群中所有个体种子产生完成后，根据当前所处迭代次数产生标准差σiter，σiter按下式计算：

(1)

(5)种子依据σiter，按照正态分布N(0,σ2)随机扩散分布在父代个体的周围形成子代种群。

(6)子代种群形成后，判断是否达到pmax。若父代种群与子代种群的个体数量之和未达到pmax，则重复(2)～(5)，若超过pmax，将父代和子代个体按适应度值优劣排序，保留适应度值优秀的个体，使种群数量控制在pmax以内。

(7)判断是否达到itmax，若未达到，则重复(2)～(6)，反之，将适应度值最优个体的信息输出作为结果。

2 改进的IWO算法运用Theis公式

2.1 算法改进

IWO算法在广度搜索空间中运用Theis公式时，搜索空间的下限值一般设置为零，为实现算法从广度搜索逐渐过渡到深度搜索，算法参数中的σinitial和σfinal须分别设置成较大值与较小值。较大的σinitial常使算法在迭代初期扩散分布时产生负解，违背了水文地质参数的非负性，导致算法无法完成深度搜索，难以获得接近实际的T和S。为此，本文尝试引入两个新的算法参数：初始扩散指数ninitial，最终扩散指数nfinal，以扩散指数niter的计算公式代替σiter的计算公式变IWO算法σiter的静态设置为动态调整。改进的IWO算法步骤如下：

(1) 确定初始种群大小N0、最大迭代次数itmax、问题的求解维数dim、最大种群数量pmax、最大种子数zmax、最小种子数zmin、初始扩散指数ninitial、最终扩散指数nfinal、自变量初始搜索空间xini，根据N0、dim、xini随机产生初始解。

(2)～(3)同IWO算法。

(4)父代种群中所有个体种子产生完成后，根据当前所处迭代次数产生扩散指数niter，niter按下式计算：

(2)

(5)种子以父代个体除以niter的商作为σiter，按照正态分布N(0,σ2)随机扩散分布在父代个体的周围形成子代种群。

(6)～(7)同IWO算法。

2.2 模型设计

2.2.1 求解公式

根据非稳定流抽水试验资料，选择Theis公式进行求解，其公式为：

(3)

(4)

(5)

式中：s为抽水影响范围内任一点任一时刻的水位降深，m；Q为抽水井的流量，m3/s；T为导水系数，m2/s；t为自抽水开始到计算时刻的时间，s；r为计算点到抽水井的距离，m；S为含水层的贮水系数。

从式(4)可以看出，计算W(u)时，需要进行广义积分，这将极大增加算法运行时间。故本文采用Rajesh Srivasiava[11]给出的W(u)近似表达式计算，其相对误差小于0.001%，足以满足生产上允许相对误差2%左右的要求[12]。该近似表达式为：

u≤1:W(u)=-Inu+a0+a1u+a2u2+a3u3+a4u4+a5u5

(6)

(7)

式中，a0=-0.577 22；a1=0.999 99；a2=-0.249 91；a3=0.055 19；a4=-0.009 76；a5=0.001 08；b0=0.267 77；b1=8.634 76；b2=18.059 02；b3=8.573 33；c0=3.958 50；c1=21.099 65；c2=25.632 96；c3=9.573 32。

2.2.2 适应度函数

以算法搜索的T和S结合求解公式计算各时刻模拟降深值，以各时刻实测降深值与模拟降深值的离差平方和的均值为适应度值[5]：

(8)

T≥0,S≥0

(9)

式中：J为观测时刻的个数；si为第i个观测时刻的实测降深值。

2.3 模型测试

2.3.1 测试方法

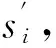
2.3.2 参数设置

测试采用统一的参数设置标准：导水系数搜索空间下限值Tmin=0，导水系数搜索空间上限值Tmax取随机值的500倍，贮水系数搜索空间下限值Smin=0，贮水系数搜索空间上限值Smax=0.5。经调试，改进的IWO算法参数取值如下：N0=5；pmax=30；zmax=4；zmin=0；ninitial=4；nfinal=100；itmax=200。GA参数取值如下：种群规模(M=100)；交叉概率(Pc=0.9)；变异概率(Pm=0.7)；遗传代数(G=400)。

2.3.3 结果分析

图1展示随机生成的1 000组T和S，图2和图3分别展示改进的IWO算法和GA所计算的1 000组T和S的相对误差值(大量数据点在坐标原点附近聚集)，表2对改进的IWO算法和GA的测试结果进行了分析。

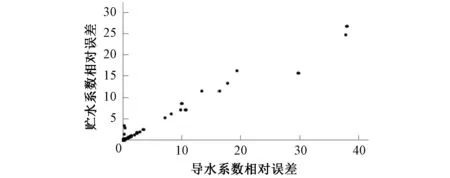
图2 1 000组相对误差值(改进的IWO算法)Fig.2 1 000 relative errors (The modified IWO)

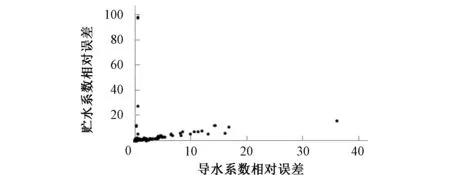
图3 1 000组相对误差值(GA)Fig.3 1000 relative errors (GA)

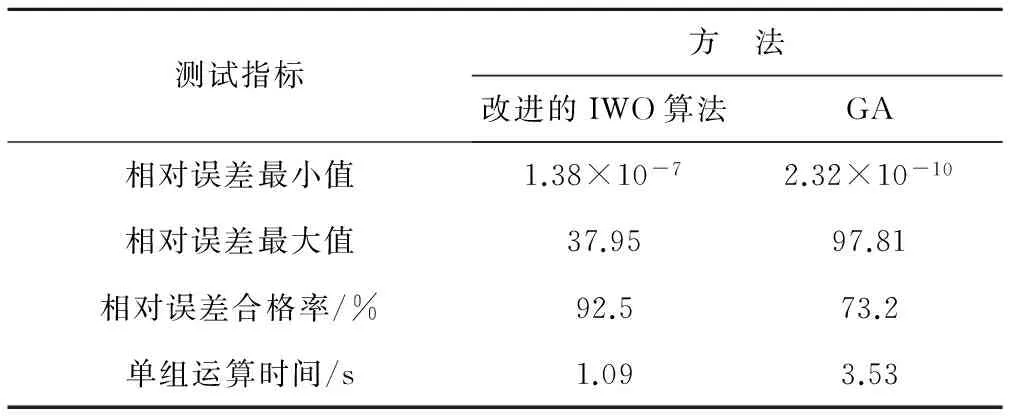
测试指标方 法改进的IWO算法GA相对误差最小值1.38×10-72.32×10-10相对误差最大值37.9597.81相对误差合格率/%92.573.2单组运算时间/s1.093.53

从上述理论测试的表达结果可以看出，当T和S的初始取值范围取较大区间时，改进的IWO算法合格率较GA更高，单组运算时间更短，相对误差波动区间更小，说明改进的IWO算法在广度搜索空间中运用Theis公式是有效的。

3 实例应用

3.1 数据来源

为开展实例应用，选取3个不同尺度的非稳定流抽水试验。依次为文献[12]、[13]和[14]中抽水10 min以后的实测降深等数据。

3.2 应用开展

为进一步展现改进的IWO算法在广度搜索空间中运用Theis公式的优越性，将搜索空间进行扩展：Tmin=0，Tmax取配线法确定结果的1 000倍，Smin=0，Smax=0.5。为判别算法在广度搜索空间中运用Theis公式的稳定性，将算法在每组实例应用中均运行100次。仍新增GA与改进的IWO算法在同等搜索空间下反演T和S的对比。经调试，改进的IWO算法参数设置如表3，GA参数设置如表4。

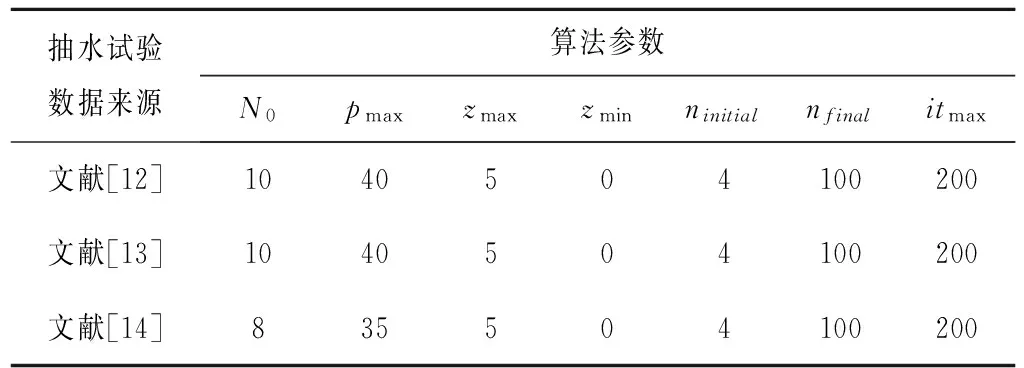
表3 改进的IWO算法参数设置Tab.3 Parameters of the modified IWO

表4 GA参数设置Tab.4 Parameters of the GA

3.3 结果分析

改进的IWO算法与其他方法求解结果的对比见表5与图4，与GA处理上述3组抽水试验的成果分别见图5、6。

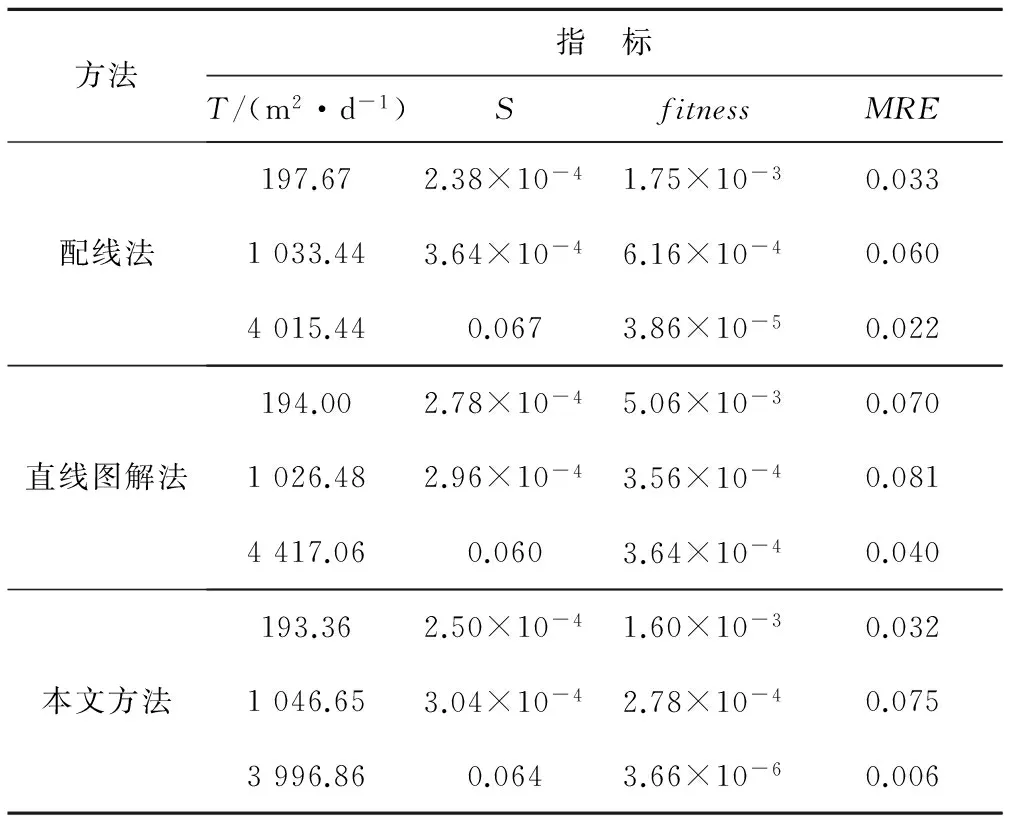
表5 不同方法的求解结果对比Tab.5 Results of different methods

图4 82组实测降深的相对误差值Fig.4 82 relative errors of drawdowns

从表5可以看出，当T与S较小时，本文方法的适应度值(fitness)略低于常用配线法及直线图解法，各观测时刻实测降深的平均相对误差(MRE)与常用方法接近，当T与S较大时，fitness和MRE均较常用方法明显降低。从图4可以看出，在文献[13]中，本文方法的多数观测时刻实测降深的相对误差(RE)介于最小值与最大值之间，在文献[12]和[14](尤其文献[14])中，多数RE的最小值由本文方法获得。综上所述，改进的IWO算法可以在广度搜索空间中反演T和S，并且当T和S较大时其求解结果较常用方法更符合实际情况。

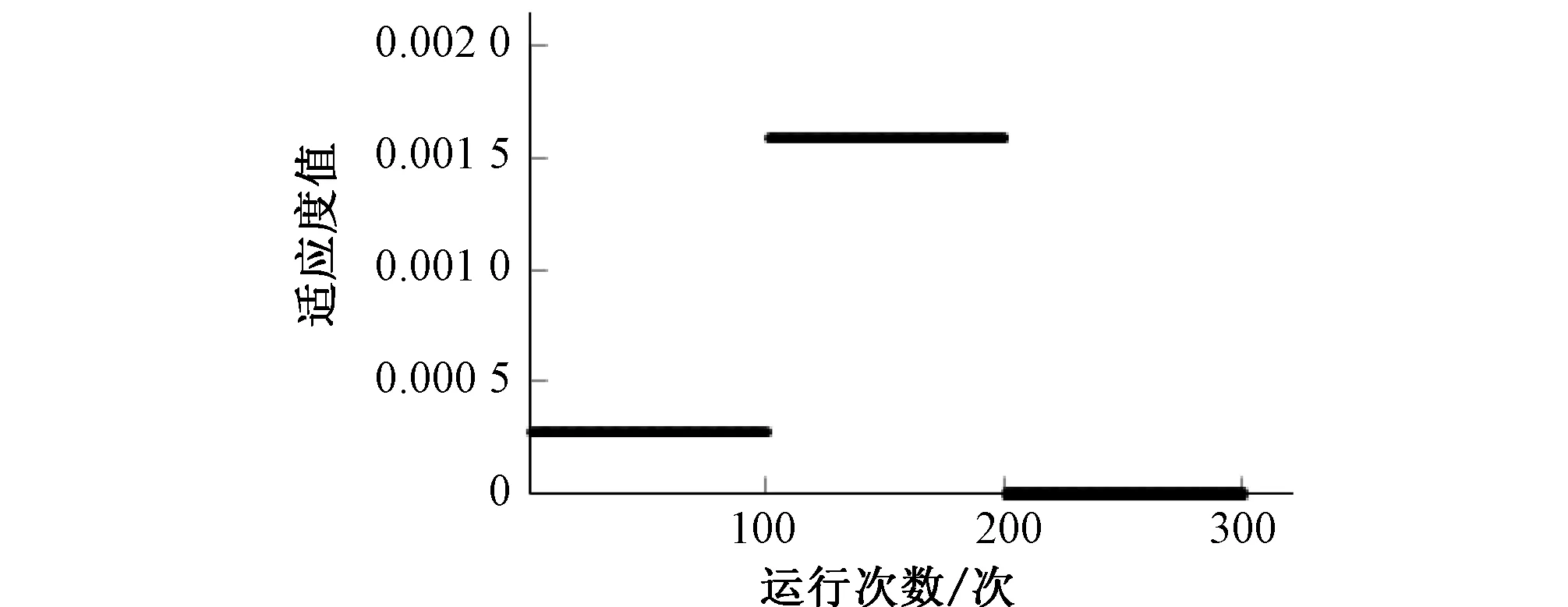
图5 300个适应度值(改进的IWO算法)Fig.5 300 fitness values (The modified IWO)

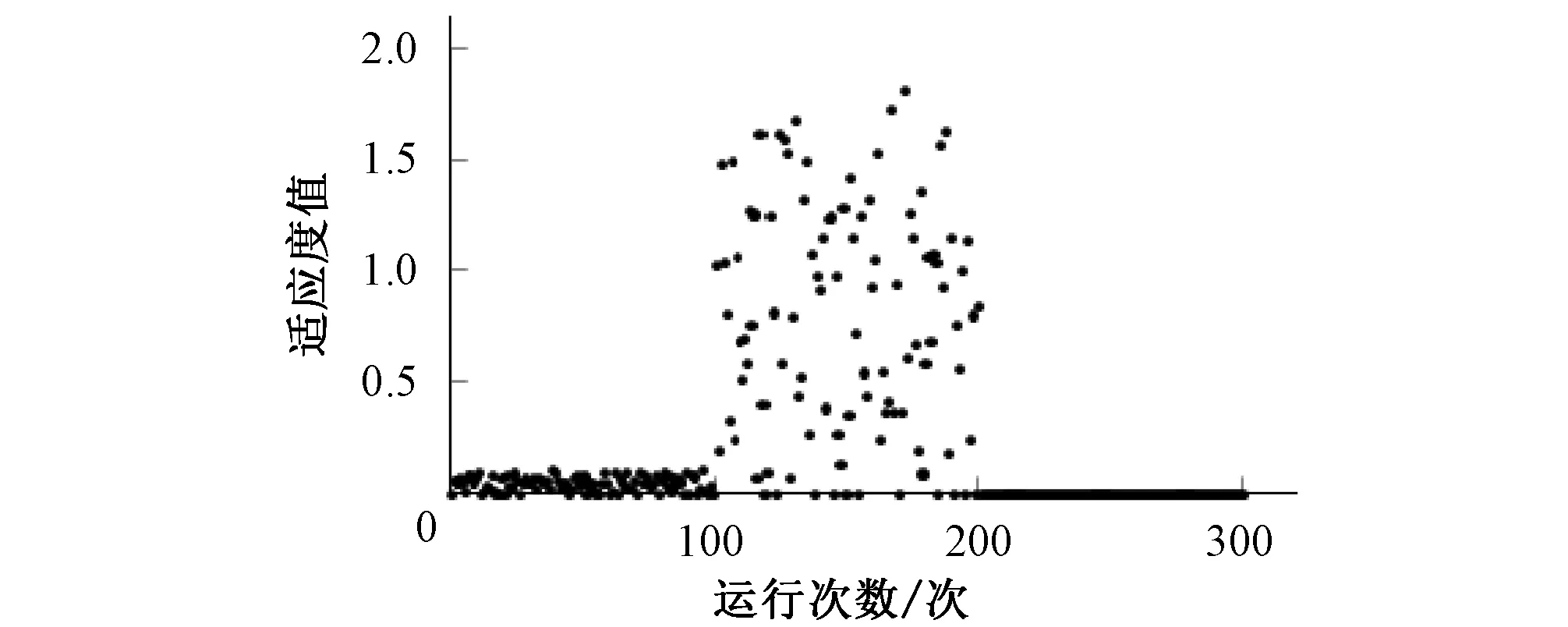
图6 300个适应度值(GA)Fig.6 300 fitness values (GA)

从与GA的对比还可看出，当T和S的初始取值范围取较大区间时，GA需要更大的种群规模及更多的迭代次数(更长的运行时间)来完成相应的求解，且在100次的运算中适应度值存在明显波动，尤其当T和S较小时(文献[12])，这种波动更为显著。改进的IWO算法在广度搜索空间中反演T和S时较GA运行时间更短，所求适应度值更低，并且100次的运算结果更稳定。

4 结 语

改进的IWO算法能在广度搜索空间中高效模拟配线分析和Theis求解，反演出接近实际的T和S，降低了预估T和S初值范围的难度。算法编程较易实现，更换算法程序中抽水试验的数据部分和对算法参数略作调整可处理不同尺度的非稳定流抽水试验。在理论测试中，改进的IWO算法较GA更快更多地搜寻出满足一定精度要求的参数。实例应用中，当T和S较大时，改进的IWO算法比常用配线法和直线图解法求解精度更高，在广度搜索空间的条件下，改进的IWO算法较GA更优更稳定。基于上述特点，改进的IWO算法可作为在广度搜索空间中反演T和S的一种新方法。

随着搜索空间的扩展和对参数求解精度要求的提高，如何进一步改善算法搜索原理，提高算法运行效率需要进一步的研究。如何将其他算法引入本算法并拓展应用需要进一步的尝试。

□

[1] 齐学斌．非稳定流抽水试验参数计算的迭代算法及计算机模拟[J]．水利学报，1995，(7)：67-71，66．

[2] 朱春龙．非稳定流抽水试验参数计算的优化算法[J]．水科学进展，1999，10(1)：75-77．

[3] 霍小虎，黄国如．遗传算法在水文地质参数确定中的应用[J]．地下水，2001，23(4)：195-197．

[4] 刘立才，陈鸿汉，张达政．梯度法在水文地质参数估值中的应用[J]．水文地质工程地质，2003，(3)：39-41．

[5] 郭建青，李 彦，王洪胜，等．粒子群优化算法在确定含水层参数中的应用[J]．中国农村水利水电，2008,(4)：4-7．

[6] 叶 咸，许 模，廖晓超，等．遗传算法优化BP神经网络在求解水文地质参数中的应用[J]．水电能源科学，2013，31(12)：55-57，65．

[7] A R Mehrabian，C．Lucas．A novel numerical optimization algorithm inspired from weed colonization[J]．Ecological Informatics，2006，1(4)：355-366．

[8] 彭 斌，胡常安，赵荣珍．基于混合杂草算法的神经网络优化策略[J]．振动、测试与诊断，2013，33(4)：634-639，725．

[9] 刘 燕，焦永昌，张亚明，等．混合入侵杂草算法用于阵列天线波束赋形[J]．西安电子科技大学学报(自然科学版)，2014,41(4)：94-99．

[10] 周金虎．基于入侵杂草算法的数据挖掘聚类算法研究[D]．兰州：兰州理工大学，2014．

[11] Rajesh Srivastava．Implications of using approximate expressions for well function[J]．Journal of Irrigation and Drainage Engineering．1995，121(6)：459-462．

[12] 薛禹群，吴吉春．地下水动力学[M]．3版. 北京：地质出版社，2010．

[13] 曹万金．地下水资源计算与评价[M]．北京：水利电力出版社，1987:97-109．

[14] U S Department of the Interior(USDI)．Groundwater Manual[M]．Bureau of Reclamation．Supt．of Documents，U S Govt．Printing Office，Washington，D C，1977：119．