相间交界面对非饱和土应力状态的影响1)

刘 艳赵成刚 李 舰 蔡国庆

(北京交通大学土建学院岩土系，北京100044)

相间交界面对非饱和土应力状态的影响1)

刘 艳2)赵成刚 李 舰 蔡国庆

(北京交通大学土建学院岩土系，北京100044)

非饱和土是一种三相多孔介质，不同相之间的交界面尤其是气液交界面的存在直接影响了非饱和土的宏观行为.首先对土中交界面的形式和作用进行了探讨，指出气液交界面对非饱和土的行为有重要影响，并给出了界面功和气液比表面积的表达式.在已有的非饱和土变形功表达式基础上，引入界面能影响，得到了考虑交界面影响的非饱和土自由能方程.利用所得的自由能方程，给出了考虑交界面影响的非饱和土固相和液相相应的应力变量.对考虑交界面面积的液相流动方程进行了探讨，给出了非平衡条件下的土水特征曲线表达式，指出在平衡条件下土水特征曲线中应当考虑交界面面积的影响，传统土水特征曲线是三维关系在吸力--饱和度平面上的投影.将比表面积与土水特征曲线的关系，利用已有试验数据验证了该表达式的合理性.利用界面面积的表达式计算有效应力，将其与已有试验结果进行对比，表明给出的比表面积表达式可很好地反映实际情况.不同于已有现象学研究，本文推导具有严格的理论基础，研究表明完整的有效应力表达式中应考虑土体内部作用力的影响，其不仅包含基质吸力，同时还包含其他形式的作用力，其大小与界面比表面积有关.该表达式为下一步研究界面效应对土体变形、强度和流动特性的研究提供了基础.

非饱和土,有效应力,比表面积

引言

选择合适的应力状态变量是描述非饱和土变形、强度等行为的重要前提，国内外众多学者都对非饱和土有效应力的选择进行了探讨[1-11].这其中比较严格的做法是根据基于热力学原理的变形功表达式来选择具体的广义应力和与其相对偶的广义变形.根据有效应力的意义，变形功中与骨架应变相对偶的应力，可以定义为有效应力.因此，根据变形功选择应力变量和有效应力，有助于认识非饱和土的力学性质，为本构关系和强度理论的建立提供理论依据.Houlsby[12-13]最早对饱和与非饱和土变形功的表达形式进行了研究和讨论，指出可以根据功的表达式来选择描述非饱和土的应力变量和应变变量，而且指出这种选择并不唯一.赵成刚等[14-15]基于多相孔隙介质理论的平衡方程和非饱和土力学的假定,推导出非饱和土总变形功的一种表达式，并基于此建立了非饱和土广义有效应力的概念.李舰等[16]针对膨胀性非饱和土的特性,区分了土中毛细液相和吸附液相性质的不同以及宏观结构和微观结构变化机理的不同,基于多相孔隙介质理论提出了土体总应力和外力输入功的表达式.

但是以上研究都没有考虑非饱和土中的界面效应，非饱和土是三相多孔介质，不同相之间必然存在交界面，这些交界面直接影响到土体的宏观特征.目前大部分研究重点关注的是交界面对非饱和土流动行为的影响[17-18]，而实际上交界面的存在对土体应力的影响也不可忽视.Fredlund和 Morgenstern[19]将收缩膜(即水气交界面)作为非饱和土的第四相来对非饱和土进行应力分析.Buscarnera和Nova[20]、Lu等[22-24]、Osipov[25]等也对界面这种土体内部作用力的存在对有效应力的影响进行了研究.Gray等[21], Nikooee等[26],张昭等[27]基于热力学原理，考虑了交界面以及界面张力对有效应力的影响，对非饱和土有效应力表达式进行了修正，给出的表达式具有更加严格的理论基础.

本文将首先探讨交界面存在对非饱和土的影响，随后在已有的非饱和土变形功表达式中引入界面能的影响，推导考虑界面效应的非饱和土自由能表达式.基于非饱和土的能量方程，可以得到相应的非饱和土有效应力以及液相方程的表达式.基于热力学能量方程可以更系统地分析交界面面积对非饱和土有效应力和液相本构(即土水特征曲线)的影响.最后将利用已有的试验数据对所得的表达式进行验证.

1 交界面作用

1.1 土中的交界面

非饱和土中一般存在固液气三相物质，相与相之间必然存在交界面.界面力学中一般把与气相相交的界面称为表面，其他交界面称为界面.这些界面的存在对于描述多孔介质流动、输运、相变和质量交换等行为有重要影响[28].在交界面区域内，两侧分子受力不平衡，为了克服这种不平衡，在交界面上会产生界面力.界面力主要来源于介质内部的物理化学作用，包括表面张力、范德华力、离子静电引力、极性分子作用力、双电层排斥力等[29-42].

土中主要关注两类交界面的影响，一是固液交界面，二是气液交界面.固液界面对土体的影响主要反映在黏土矿物与水的相互作用上.黏土矿物表面分子与水分子之间的相互作用形成双电层，使得黏土表现出一些特殊性质，如表面活性、吸附能力、离子交换等.双电层作用在土粒表面形成结合水，表现出与自由水不同的性质，如黏滞性、弹性和抗剪强度.气液交界面是存在于非饱和土中的重要特性，通常也将其称为收缩膜.其产生的表面张力和毛细现象对非饱和土行为有重要影响.气液交界面上产生的毛细力，是非饱和土有效应力的重要组成部分.此外毛细力与含水量之间的关系(土水特征曲线)也直接影响着非饱和土的变形、强度和渗流特性.

1.2 界面功

从能量的角度来看，界面力的存在使得交界面上产生了相对于原先不存在交界面系统自由能的过剩自由能，称为界面自由能[28].这些存在于土体内部的作用力与土体所受外力一样，会对土体的变形和强度产生影响，因此有必要在非饱和土变形功的表达式中考虑界面能的影响.界面自由能可以定义为每增加单位面积克服界面张力所做的功，因此界面功可以表示为

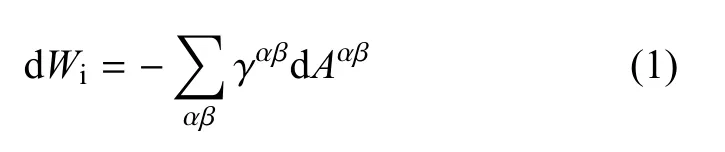
式(1)按照土力学中以压为正的表示方法，故右端有一个负号.γαβ是交界面的表面张力，Aαβ是交界面的面积，aαβ是交界面的比表面积，即单位体积的界面面积，可以表示为

单位体积的界面功可以表示为

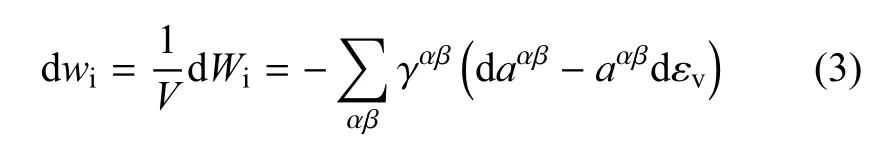
式中，V是非饱和土的体积，εv是非饱和土的体应变.

1.3 界面比表面积

界面比表面积是计算界面能的一个重要参数，它建立土体平衡方程的关键变量，对热力学基本方程的建立至关重要，同时也直接影响了本构方程的构建.比表面积通常与土体组分、结构以及孔隙分布密切相关.由于受到实验方法和测试技术的限制，比表面积的实验确定仍比较困难.目前主要方法有电镜扫描、核磁共振、X射线扫描、示踪技术等.

通常土中气液交界面包含两部分作用，一部分与结合水膜相交，另一部是毛细水相交.总的气液交界面面积应为两部分之和，此时比表面积的大小将随着饱和度的增大而减小，如图1中曲线I所示.而与毛细水相交的交界面面积与饱和度之间并不是单调关系，如图1中曲线II所示.本文假设不考虑结合水膜作用，重点关注毛细水相关交界面作用.因此气液交界面的形成完全是由毛细作用产生，如果要考虑结合水膜影响可参考文献[29].

图1 比表面积与饱和度关系示意图Fig.1 Sketch for relationship between specifi interfacial area and degree of saturation

试验测试方法常常费时或昂贵，因此理论计算方法常常被用于估算土体的比表面积，比如孔隙网格模型、Lattice--Boltzmann模型等.Joekar--Niasar等[30]利用孔隙网络模型对三者的关系进行了研究，并将比表面积表示为饱和度与吸力的二次多项函数.但该函数只是一个数学拟合结果，没有物理意义.为此，Joekar-Niasar和Hassanizadeh[31]对该表达式进行了改进，给出了一个指数形式的表达式，使其可以计算曲线II的气液交界面比表面积，并具有一定的物理意义.

一般气液比表面积可表示为饱和度与吸力的函数，但由于毛细力可以通过土水特征曲线表示为饱和度的函数，因此本文假设气液比表面积与饱和度的关系可以用下式表示

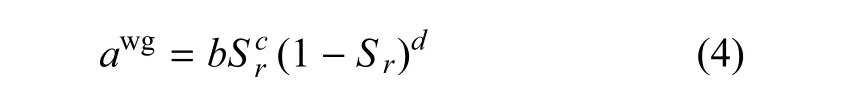
式中，Sr为饱和度，b,c,d均为材料参数.该式表明当土体完全干燥(Sr=0)或完全饱和(Sr=1)时，由毛细作用而产生的气液交界面面积均为零(awg=0).

2 考虑界面影响的非饱和土应力

2.1 热力学描述

赵成刚等[14-15]从热力学基本平衡方程出发，在不考虑温度影响和质量交换，忽略固体颗粒和流体压缩性的假设下，得到了单位体积的非饱和土变形功的基本表达式

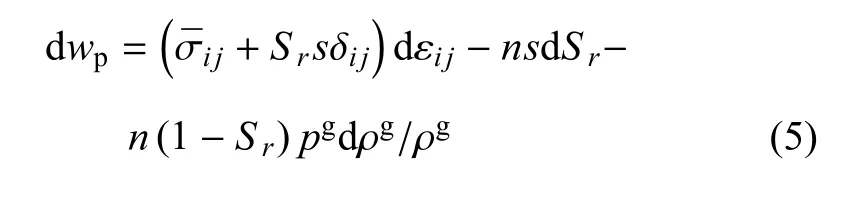
式(5)表明非饱和土变形功由3部分组成：第1项是由于固体骨架变形所产生的变形功，第2项是由于流体饱和度的改变所产生的变形功，第3项是气体压缩产生的变形功.该表达式中并没有考虑界面效应的影响，已有研究表明，存在于土体内部的作用力与土体所受外力一样，会对土体的变形和强度产生影响，因此有必要在非饱和土变形功的表达式中考虑界面能的影响.

引入界面能后，总的变形功表达式为式(3)和式(5)相加.此外，Hassanizadeh和Gray[32]指出大部分土中流体和固体交界面的比表面积为常数，因此毛细力主要受到气液交界面的影响.如果不考虑气相变形功和固相交界面的影响，总变形功可以表示为

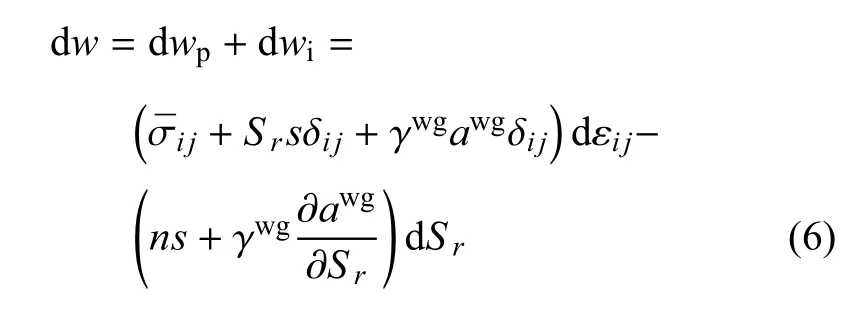
根据能量守恒原理，系统的内能的变化由功和热交换两部分引起

根据热力学第二定律，热量变化可以表示为

式 (8)中 η表示熵，表示 φ熵增，在平衡条件下φ=0，对于非平衡过程，系统存在耗散时φ≥0.

系统的自由能可以表示为

根据式(6)～式(9)，等温条件下有

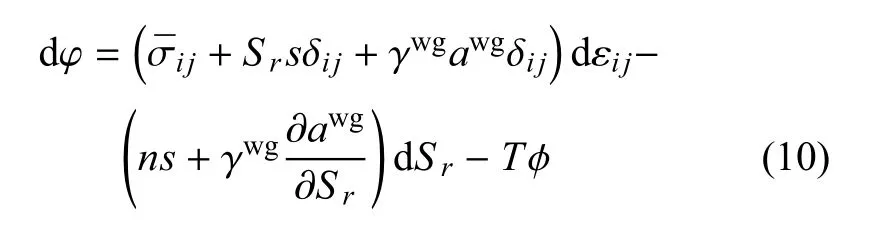
利用能量方程(10)，可以得到如下关系[33]

2.2 非饱和土的流动方程

利用式(10)可以得到流体自由能方程为

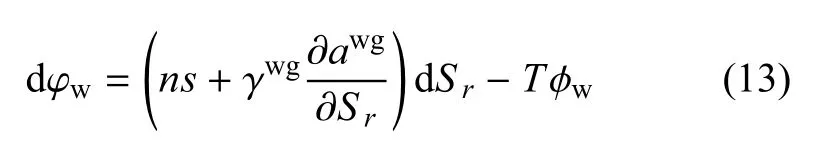
由于熵增φw≥0，因此可以得到不等式

式(12)表明，与流体饱和度变化功共轭的应力为

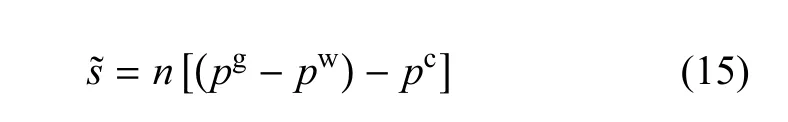
其中，pc是宏观毛细力，可以表示为

式(16)表明毛细力不仅与饱和度有关，同时也与比表面积和孔隙率有关.

在线性假设条件下，根据熵不等式(14)可以给出液相广义力与广义流之间本构关系如下

式 (17)与 Hassanizadeh和 Gray[32]给出的表达式是一致的，τ称为毛细阻尼系数 (capillary damping coefficient)[17]，控制了饱和度改变的速率.如果τ取值很小，说明系统受扰动后会迅速恢复新的平衡.利用式(15)，式(17)可以改写为如下形式

式(18)表征了非平衡条件下的土水特征曲线，右边第2项的存在说明此时基质吸力与饱和度的变化历史有关，已有试验证明这种水力历史会对土的变形和强度产生影响[34].由于流体压力差(pg-pw)与毛细力pc的不平衡，导致了系统饱和度的改变，这种改变可以使系统重新达到新的平衡状态，恢复流体压力差(pg-pw)与毛细力pc的平衡.只有在平衡条件下，饱和度才不随时间变化，式(17)简化为

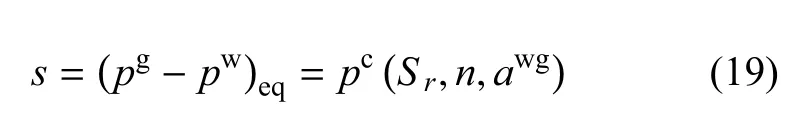
在平衡条件下，如果不考虑比表面积awg的影响，式(19)就是传统考虑固相变形影响的土水特征曲线的基本表达式.对该式进行变换，即可将比表面积表示为吸力和饱和度的函数，为式(4)提供了理论依据.

土水特征曲线的一个重要特点就是存在滞后现象，Hassanizadeh和Gray[32]指出导致毛细力与饱和度之间关系不唯一的原因可能在于土水特征曲线方程中没有包含比表面积的影响.也就是说考虑界面效应后，干燥和湿化过程中pc-Sr-awg三维空间中的曲面可能是唯一的，但这一观点目前仍未得到证实.

2.3 非饱和土的有效应力

与固相变形功共轭的应力实际上就是非饱和土的有效应力，其表达式(11)如下

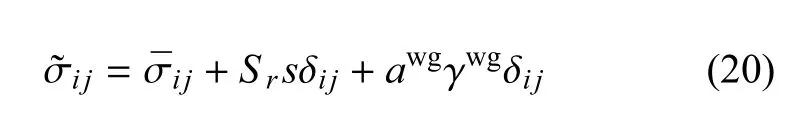
式(20)表明非饱和土的有效应力来源于两个部分：第一部分是净应力，属于外力作用，源自于土体自身的重力或作用在土骨架上的外部载荷；第二部分来源于土体内部的各种作用力.Lu和Likos[22]指出在非饱和土中存在两种类型的主动力，一是作用于骨架上的外力，另一种就是土体内部颗粒间接触的相互作用力.所有这些内部的作用力都是主动的，因为它们并不是由于外力作用而产生，而是源自土体内部的物理化学作用，包括范德华力、双电层排斥力、化学胶结作用力，非饱和土中则还需要考虑表面张力的影响.Osipov[25]同样指出土受力形式可以分为内力和外力两种，外力主要包括重力、静水压力、动水压力和外部结构施加的载荷等，内力主要包括毛细力和水化膜的分离力.有效应力应当是以上外力和内力共同作用下产生的，本节给出的基于热力学原理得到的有效应力表达式(20)正好印证了这一观点.

式 (20)中内力部分实际上就相当于 Lu和Likos[22]提出的吸应力，可表示为

参考Muraleetharan和Wei[35]，假定宏观表面张力γwg可以表示为吸力函数，即

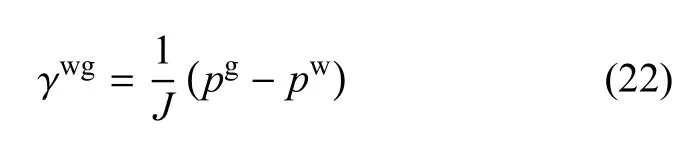
从形式上看式(22)与Young-Laplace方程是一致的，但两者有本质区别.Young-Laplace方程描述的是微观尺度上表面张力与毛细力之间的关系，只有在平衡时毛细力才等于流体的压力差.为了得到宏观的关系式，需借助于平均化方法，给出平衡方程和熵不等式，由此推导出的宏观毛细力与宏观表面张力的关系与后文给出的式(16)一致.根据上一节的分析可知，只有在平衡条件下，宏观基质吸力与毛细力相等，此时式(22)中J就是流体交界面的宏观平均曲率[36].

利用式(22)，可将式(20)表示成Bishop应力的形式，则有

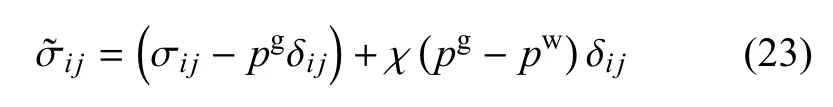
其中有效应力参数χ表达式为

目前非饱和土有效应力常常采用 Bishop应力形式来表示，其中存在的最大争议在于Bishop参数χ的取值问题上.比较普遍的一种做法是用饱和度来替代Bishop参数，由此得到的有效应力代表了总应力减去以各自的体积分数作为权重系数的孔隙水压和孔隙气压的综合作用，这种做法的好处在于饱和时有效应力可以退化为饱和土有效应力.当忽略界面作用时，该表达式可以从功的表达式中得到证明[13,15].Loret和Kahlili[37]对这种将饱和度作为权重系数用以反映孔隙流体的综合作用的做法提出质疑，认为χ取值应当采用面积分数，而不是体积分数，但由于实际当中面积分数难以测量和确定，所以一般近似用体积分数表示的饱和度进行替代.Alonso等[38]也指出由于应力是作用在颗粒单位面积上的作用力，因此基于面积分数定义的饱和度作用权重系数更加合理.Gray等[9]指出并不是所有土体孔隙中的流体都会对有效应力产生影响，真正发挥作用的是形成交界面的那部分流体，而这部分流体的含量仅仅是孔隙流体的一部分，此时用饱和度来度替换Bishop参数作为权重系数来表示流体产生的作用力，就会出现误差.已有实验结果表明，Bishop参数与饱和度之间并不是单调唯一的关系[39]，为此出现了不同的Bishop参数χ表达形式，如Khalili和Khabbaz[40]将χ表示为吸力的函数，Alonso等[38]用有效饱和度来表示χ，Gray和Schrefle[9]用交界面面积比值来表示χ.

式(24)表明在考虑界面效应影响后，有效应力参数χ并不能简单地用饱和度来替代，还需要考虑界面面积的影响.但是由于受到实验手段和测量方法的限制，交界面比表面积的确定仍然比较困难，现有研究发现交界面比表面积可以表示为饱和度和宏观毛细力的函数，这一点也可从式(19)中得到印证.因此借助于式(4)来确定awg，进而确定有效应力的取值，可能是较为有效的一种方法.

3 数值验证

本节将利用已有实验成果对本文提出的考虑界面效应的方程进行验证.计算时首先必须给出土水特征曲线的方程，这里采用van-Genuchten形式，即

接下来采用Porter等[41]的实验结果来验证式(4)的合理性.根据实验结果可以得到所需的参数，残余饱和度取值为其他参数取值见表1.

表1 Porter等[41]实验拟合参数Table 1 Material coefficients for Porter et al.[41]

图2给出了土水特征曲线的预测结果，总体上与实际相符.图3利用本文给出的表达式(4)对实验结果进行了预测，结果表明该表达式可以很好地反映比表面积与饱和度的关系.实验结果表明在吸湿与脱湿阶段，比表面积与饱和度的关系并不唯一，但总体差别并不大.预测曲线表明，当饱和度Sr=0.35时，吸湿(awg=0.30)与脱湿曲线(awg=0.35)的比表面积值差值最大，相差约为15%.高饱和度时(Sr＞0.8)，两者几乎没有区别.

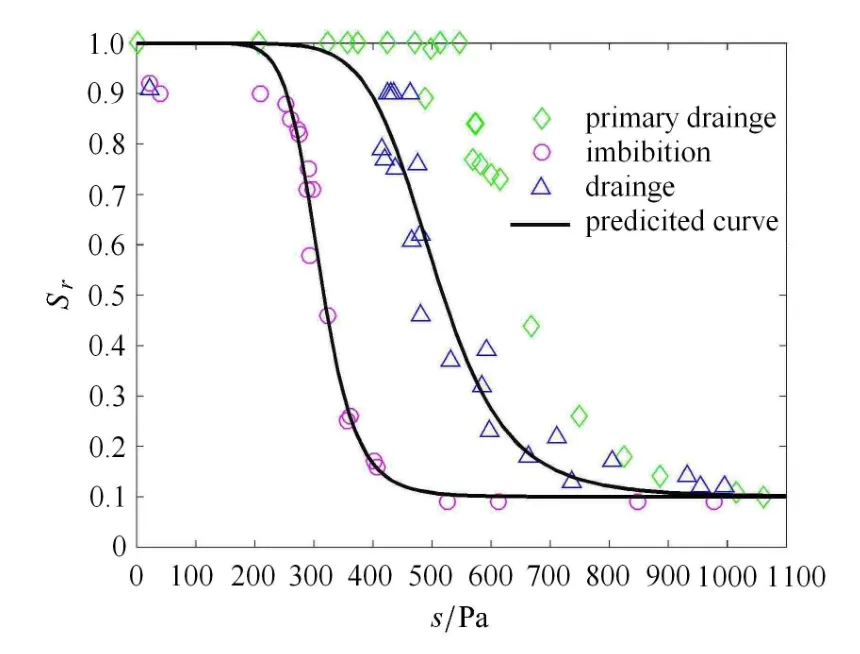
图2 土水特征曲线Fig.2 Soil water characteristic curve

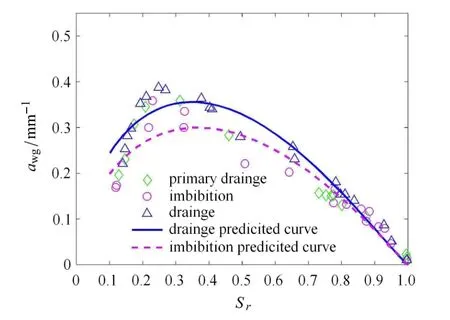
图3 比表面积与饱和度关系Fig.3 Relationship between specifi interfacial area and saturation

图4给出了比表面积、饱和度与毛细力三维关系曲线.该曲线在s-awg平面上的投影反应了比表面积与吸力的关系，说明尽管式(4)中没有包含毛细力作用，但通过土水特征曲线，可以间接地将其影响考虑进来.土水特征曲线实际上就是s-Sr-awg三维空间中的曲面在s-Sr平面上的投影.干燥与湿化曲线在s-Sr-awg三维空间中的曲线是否位于同一曲面上仍需要更多的试验验证.

图4 比表面积、饱和度与毛细力三维关系的预测结果Fig.4 Predictions for relationship among specifi interfacial area, saturation and capillary pressure

图5和图6给出的是考虑界面面积影响后土体有效应力参数以及应力大小的变化情况.图中采用的试验数据来源于Lu[23]，选择了其中4种不同类型的土，其土水特征曲线的参数在原文中已给出，其中残余饱和度取值均为比表面积相关参数b,c,d可通过试验点进行拟合，所得参数取值如表2所示.

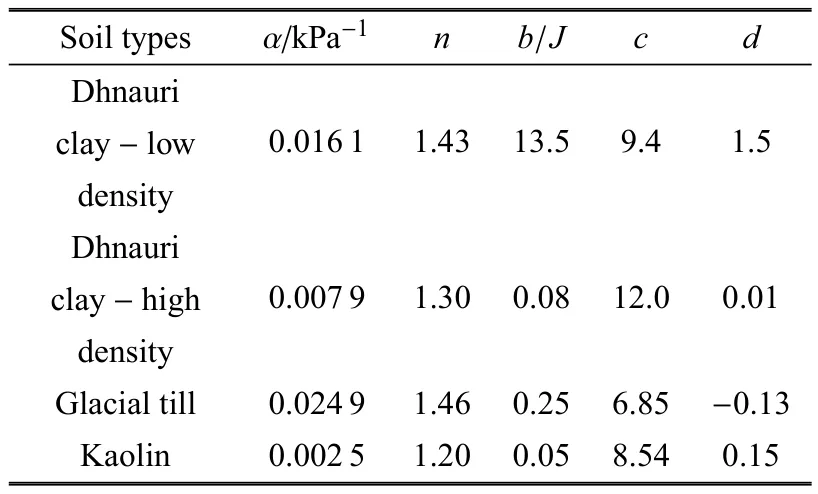
表2 Lu等[23]实验拟合参数Table 2 Material coefficients for Lu et al.[23]

图5利用本给出的表达式(21)，计算得到了4种类型土的吸应力，并将其与实验数据进行了对比.预测曲线可以较好地模拟实验点，从而验证表达式的合理性.图6利用本文给出的式(24)计算得到4种土有效应力参数，将其与饱和度和的关系进行了对比.饱和度与有效应力参数并不相等，如果直接采用饱和度替换有效应力参数，计算出的有效应力将会偏小，由此估算出土体的强度也将出现误差，由此表明本文给出的考虑界面面积影响后的有效应力表达式，其计算结果也更加接近实际情况.

图5 吸应力的对比结果Fig.5 Comparison between predicted results and experimental data for suction stress

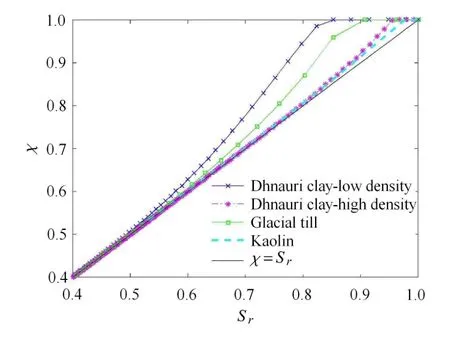
图6 饱和度和有效应力参数Fig.6 Predictions for degree of saturation and e ff ective stress parameter

4 结论

本文探讨了非饱和土相间交界面对其应力状态的影响.在已有的变形功表达式基础上，引入了界面能的影响，通过推导得到了非饱和土的自由能的表达式(10).根据该表达式可以确定相应的广义力与广义流，为建立非饱和土的本构关系提供了理论依据.

利用能量方程和熵增不等式，假设满足线性关系可得到动力条件下的液相本构方程，此时基质吸力与毛细力不相等，它们之间的不平衡可能会导致土体出现排水或吸湿过程.只有在重新达到平衡，饱和度不再随时间变化，基质吸力与宏观毛细力才会相等.在平衡条件下，考虑界面效应后的非饱和土液相本构方程不再是简单的基质吸力与饱和度的关系，还增加了第三个变量即比表面积，传统的土水特征曲线实际上成为三维空间pc-Sr-awg中曲面在pc-Sr平面上的投影.三维空间的土水特征曲面是否唯一，即引入界面比表面积后三维曲面是否存在滞后现象，需要进一步研究.

考虑界面能后，非饱和土的有效应力将包含界面张力与界面面积的影响，有效应力中包含土中外力与内力的共同作用.将所得有效应力表示为Bishop应力形式后，其有效应力参数不能简单地用饱和度来进行替代，而是饱和度与界面面积的函数.利用液相方程，可将比表面积表示为饱和度的函数，通过与已有实验结果对比，验证了该有效应力表达式的合理性.

本文得到的考虑界面影响的有效应力，为下一步研究界面效应对土体变形、强度和流动特性的研究提供了基础.而如何给出更加合理的界面比表面积的定量表达式，并确定其对整个应力状态影响也是需要进一步研究的问题.

1 谢定义,冯志焱.对非饱和土有效应力研究中若干基本观点的思辨.岩土工程学报,2006,28(2):170-173(Xie Dingyi，Fen Zhiyan. Consideration of some fundamental viewpoints in studying e ff ective stress of unsaturated soils.Chinese Journal of Geotechnical Engineering,2006,28(2):170-173(in Chinese))

2 周建.非饱和土本构模型中应力变量选择研究.岩石力学与工程学报,2009(6):1200-1207(Zhou Jian.Research on selection of stress variables of constitutive model for unsaturated soils.Chinese Journal of Rock Mechanics and Engineering,2009(6):1200-1207 (in Chinese))

3 陈正汉,秦冰.非饱和土的应力状态变量研究.岩土力学,2012, 33(1):1-11(Chen Zhenghan,Qin Bing.On stress state variables of unsaturated soils.Rock and Soil Mechanics,2012,33(1):1-11(in Chinese))

4 邵龙潭,郭晓霞,郑国锋.粒间应力、土骨架应力和有效应力.岩土工程学报,2015,37(8):1478-1483(Shao Longtan,Guo Xiaoxia, Zheng Guofeng.Intergranular stress,soil skeleton stress and effective stress.Chinese Journal of Geotechnical Engineering,2015, 37(8):1478-1483(in Chinese))

5 赵成刚,刘真真,李舰等.土力学有效应力及其作用的讨论.力学学报,2015,47(2):356-361(Zhao Chenggang,Liu Zhenzhen,Li Jian,et al.E ff ective stress in soil mechanics and the discussions about its functions.Chinese Journal of Theoretical and Applied Mechanics,2015,47(2):356-361(in Chinese))

6 刘艳,赵成刚,蔡国庆等.非饱和土力学理论的研究进展.力学与实践,2015,37(4):457-465(Liu Yan,Zhao Chenggang,Cai Guoqing,et al.Research development of unsaturated soil mechanics.Mechanics in Engineering,2015,37(4):457-465(in Chinese))

7 张泷,刘耀儒,杨强.岩体结构非平衡演化的有效应力原理及长期稳定性分析.力学学报,2015,47(4):624-633(Zhang Long,Liu Yaoru,Yang Qiang.E ff ective stress principle of non-equilibrium evolution and long term stability analysis of rock mass structure.ChineseJournalofTheoreticalandAppliedMechanics,2015,47(4): 624-633(in Chinese))

8 李锡夔,杜友耀,段庆林.基于介观结构的饱和与非饱和多孔介质有效应力.力学学报,2016,48(1):29-39(Li Xikui,Du Youyao, Duan Qinglin.Meso-structure informed e ff ective stresses in saturated and unsaturated porous media.Chinese Journal of Theoretical and Applied Mechanics,2016,48(1):29-39(in Chinese))

9 Gray WG,Schrefle BA.Thermodynamic approach to e ff ective stress in partially saturated porous media.European Journal of Mechanics-A/Solids,2001,20(4):521-538

10 NuthM,LalouiL.E ff ectivestressconceptinunsaturatedsoils:Clarificatio and validation of a unifie framework.International Journal for Numerical and Analytical Methods in Geomechanics,2008, 32(7):771-801

11 Sheng D.Review of fundamental principles in modelling unsaturated soil behaviour.Computers and Geotechnics,2011,38(6):757-776

12 Houlsby GT.The work input to a granular material.. 1979,29(3):354-358

13 Houlsby GT.The work input to an unsaturated granular material..1997,47(1):193-196

14 Zhao CG,Liu Y,Gao FP.Work and energy equations and the principleofgeneralizede ff ectivestressforunsaturatedsoils.International Journal for Numerical and Analytical Methods in Geomechanics, 2010,34(9):920-936

15 Zhao C,Zhang X.Derivation of the work expression and discussion on the e ff ective principle and the phase separation theorem in unsaturated soil.Science in China Series E:Technological Sciences, 2008,51(9):1530-1541

16 Li J,Zhao C,Cai G,et al.The input work expression and the thermodynamics-based modelling framework for unsaturated expansive soils with double porosity.Chinese Science Bulletin,2013, 58(27):3422-3429

17 Hassanizadeh SM,Celia MA,Dahle HK.Dynamic e ff ect in the capillarypressure–saturationrelationshipanditsimpactsonunsaturated fl w.Vadose Zone Journal,2002,(1):38-57

18 Joekar-Niasar V,Hassanizadeh SM.Specifiinterfacial area:the missing state variable in two-phase fl w equations.Water Resources Research,2011,47(5):159-164

19 Fredlund DG,Morgenstern NR.Stress state variables for unsaturated soils.Journal of the Geotechanical Engineering Division(ASCE),1977,103:447-466

20 Buscarnera G,Nova R.An elastoplastic strainhardening model for soil allowing for hydraulic bonding–debonding e ff ects.International Journal for Numerical and Analytical Methods in Geomechanics,2009,33(8):1055-1086

21 Gray WG,Schrefle BA,Pesavento F.Work input for unsaturated elastic porous media.Journal of the Mechanics and Physics of Solids,2010,58(5):752-765

22 Lu N,Likos W.Suction stress characteristic curve for unsaturated soil.Journal of Geotechnical and Geoenvironmental Engineering, 2006,132(2):131-142

23 Lu N,Godt JW,Wu DT.A closed-form equation for e ff ective stress in unsaturated soil.Water Resources Research.2010,46(5):W5515 24 Likos WJ.E ff ective stress in unsaturated soil:accounting for surface tension and interfacial area.Vadose Zone Journal,2014,13(5)

25 Osipov VI.The 2012 Hans Cloos lecture:physicochemical theory of e ff ective stress in soils.Bulletin of Engineering Geology and the Environment,2014,73(4):903-915

26 Nikooee E,Habibagahi G,Hassanizadeh SM,et al.E ff ective stress in unsaturated soils:a thermodynamic approach based on the interfacial energy and hydromechanical coupling.Transport in Porous Media,2013,96(2):369-396

27 张昭,刘奉银,张国平.考虑气--液交界面的非饱和土有效应力公式.岩土力学,2015,36(S1):147-153(Zhang Zhao,Liu Fengyin, ZhangGuoping.Ane ff ectivestressformulationforunsaturatedsoils considering air-liquid interface.Rock and Soil Mechanics,2015, 36(S1):147-153(in Chinese))

28 Butt H,Graf K,Kappl M.Physics and Chemistry of Interfaces.Second,Revised and Enlarged Edition.Wiley-VCH Verlag GmbH& Co.KGaA,2006

29 Peng S,Brusseau ML.Impact of soil texture on air-water interfacial areas in unsaturated sandy porous media.Water Resources Research,2005,41(3):W3021

30 Joekar-Niasar V,Hassanizadeh SM,Leijnse A.Insights into the relationships among capillary pressure,saturation,interfacial area and relative permeability using pore-network modeling.Transport in Porous Media,2008,74(2):201-219

31 Joekar-Niasar V,Hassanizadeh SM.Uniqueness of specifi interfacial area–capillary pressure–saturation relationship under nonequilibrium conditions in two-phase porous media fl w.Transport in Porous Media,2012,94(2):465-486

32 Hassanizadeh SM,Gray WG.Thermodynamic basis of capillary pressure in porous media.Water Resources Research,1993,29(10): 3389-3405

33 刘艳,赵成刚,蔡国庆.理性土力学与热力学.北京:科学出版社,2016(Liu Yan,Zhao Chenggang,Cai Guoqing.Theoretical Soil Mechanics and Thermodynamics.Beijing:Science Press,2016(in Chinese))

34 Sun D,Zhang J,Gao Y,et al.Influenc of suction history on hydraulic and stress-strain behavior of unsaturated soils.International Journal of Geomechanics,2016:16(6):01001AB

35 Muraleetharan KK,Wei C.Dynamic behaviour of unsaturated porous media:governing equations using the theory of mixtures with Interfaces(TMI).International Journal for Numerical and Analytical Methods in Geomechanics,1999,23(13):1579-1608

36 Gray WG.Thermodynamics and constitutive theory for multiphase porous-media fl w considering internal geometric constraints.Advances in Water Resources,1999,22(5):521-547

37 Loret B,Khalili N.An e ff ective stress elastic–plastic model for unsaturated porous media.Mechanics of Materials,2002,34(2):97-116

38 Alonso EE,Pereira JM,Vaunat J,et al.A microstructurally based e ff ective stress for unsaturated soils.,2010,60(12): 913-925

39 Bishop AW,Blight GE.Some aspects of the e ff ective stress in saturated and partially saturated soils.,1963,13(3):177-197

40 Khalili N,Khabbaz MH.A unique relationship for χ for the determination of the shear strength of unsaturated soils., 1998,48(5):681-687

41 Porter ML,Schaap MG,Wildenschild D.Lattice-Boltzmann simulations of the capillary pressure–saturation–interfacial area relationship for porous media.Advances in Water Resources,2009,32(11): 1632-1640

42 Lu N,Likos WJ.Unsaturated Soil Mechanics.New Jersey:Wiley, 2004

THE INFLUENCE OF INTERFACES ON THE STRESS STATE IN UNSATURATED SOILS1)

Liu Yan2)Zhao Chenggang Li Jian Cai Guoqing
(School of Civil Engineering，Beijing Jiaotong University，Beijing100044，China)

Unsaturated soil is a three-phase porous media.The interfaces between every two phases,especially between liquid and gas phase,have important influenc on soil behavior.The interfacial form and e ff ect of soil are discussed and the expressions for interfacial work and specifi interfacial area are presented.By introducing the interfacial work into the existing work input equation,the Helmholtz free energy of unsaturated soils with interfacial e ff ect can be derived. Based on the free energy equation,the stress variables considering interfacial e ff ect for solid and liquid can be obtained. The influence of interfacial area on fl w equation of liquid phase are discussed,and it is pointed out that the gas-liquid interface area should be introduced as a third variable in a complete soil water retention curve(SWRC).The traditional SWRC is a projection of the three-dimensional expression in the(s,Sr)plane.The e ff ective stress considering specifi area can be calculated by the relationship between specifi area and SWRC.The proposed equation of e ff ective stress is used to simulate experimental data in the literature,and results show our finding are in good accordance with practice.Di ff erent from the existing phenomenology studies,the deductive process has a rigorous theoretical basis in this paper. The results shown that the complete expression of e ff ective should consider the e ff ects of internal force in soil,which including not only matric suction,but also the other force related to the specifi interfacial area.

unsaturated soils,e ff ective stress,specifi interfacial area

TU43

A

10.6052/0459-1879-16-190

2016–07–12收稿，2016–12–30录用,2017–01–02网络版发表.

1)中央高校基本科研业务费专项资金资助项目(2014 JBM090).

2)刘艳，副教授，主要研究方向：非饱和土力学.E-mail：yanl@bjtu.edu.cn

刘艳,赵成刚,李舰,蔡国庆.相间交界面对非饱和土应力状态的影响.力学学报,2017,49(2):335-343

Liu Yan,Zhao Chenggang,Li Jian,Cai Guoqing.The influenc of interfaces on the stress state in unsaturated soils.Chinese Journal of Theoretical and Applied Mechanics,2017,49(2):335-343