封拱温度场对青龙RCC拱坝极限承载能力的影响
杨舒涵,漆天奇,王均星,李圆圆,杨 晓
(1.武汉大学水资源与水电工程科学国家重点实验室,武汉 430072; 2.长江三峡勘测研究院有限公司(武汉),武汉 430072)
拱坝作为一种具有自调节性和超载能力的高次超静定结构,其坝型广泛应用于坝工建设中。随着筑坝技术的迅速发展,Roller Compacted Concrete(RCC)筑坝方式已成为拱坝建设的主流。温度作用作为拱坝的一项主要荷载,是拱坝应力控制性边界条件之一,一般占拱坝荷载的30%以上[1]。拱坝规范中规定的温度作用是由坝址处的气象、库水温等边界条件求出大坝运行期的最高、最低温度,再减去封拱温度得到。由此可知,封拱温度为拱坝温度作用计算的起始点[2]。封拱温度直接影响温度作用的大小,继而影响拱坝坝体应力的大小和分布,最终影响拱坝极限承载能力的大小。目前,国内外学者关于封拱温度场对坝体应力的影响已做了深入研究[3-6],认为封拱温度场的变化对坝体应力的影响显著,封拱时截面平均温度和上下游坝面等效线性温差的调整不同,其对坝体拉、压应力的影响也不同。在温降工况下提高封拱时截面平均温度,易使坝面产生拱向拉应力,促使坝体产生裂缝[7]。由此引发封拱温度场对拱坝承载能力影响的研究。目前,此方面的研究尚不多见。
本文在ANSYS有限元软件平台上,结合湖北省青龙RCC拱坝这一工程实例,依据施工过程中提出的四种不同封拱温度场方案,基于Drucker-Prager准则,采用弹塑性有限元方法,计算各方案下青龙RCC拱坝在降强过程中的极限承载能力,运用塑性区贯通、位移突变法及收敛性等破坏判据,分析各方案下青龙RCC拱坝的渐进破坏模式及强度储备系数的变化规律,探讨其破坏机制,并分析封拱温度场对青龙RCC拱坝极限承载能力的影响,同时评价拱坝抗滑稳定的安全度。
1 封拱温度场的研究
拱坝的温度作用是指坝体封拱形成整体后的温度变化,可以分解成平均温度Tm、等效线性温差Td和非线性温差Tn三部分。其中Tn不影响坝体的变位和应力计算,所以温度作用的计算通常只考虑Tm和Td。参见我国SL282-2003《混凝土拱坝设计规范》,拱坝温度作用计算公式如下:
Tm=Tm1-Tm2-Tm0
(1)
Td=Td1+Td2-Td0
(2)
式中:Tm0、Td0分别为由封拱温度场决定的平均温度和等效温差;Tm1、Td1分别为由多年年平均温度场决定的平均温度和等效温差;Tm2、Td2分别为由多年年平均变化温度场决定的平均温度和等效温差。
拱坝的温度作用决定于封拱温度场、年平均温度场和变化温度场这3个特征温度场,并由式(1)、式(2)中相应值求得[8]。则,调整拱坝的温度作用需从控制这些特征温度场入手。当坝体边界条件及坝区的气温变化规律确定以后,拱坝的年平均温度场和变化温度场就随之确定。所以3个特征温度场中,技术上人为可行的办法是控制封拱温度场以调整拱坝的温度作用[2]。
在拱坝建设实践中,温控措施通常采用双向对称通水冷却的方法,使得拱坝封拱温度场的等效线性温差Td0≈0。 故本文主要以封拱温度场中截面平均温度Tm0为研究对象,进行探讨。
2 计算模型及资料
2.1 工程概况
青龙水电站坐落于湖北省恩施市,为Ш等工程,主要建筑物为抛物线RCC双曲拱坝、发电引水系统等。由于坝高超过100 m,其建筑物级别提高一级为2级。坝址处两侧山体陡峻,河谷呈深“U”形。拱坝坝顶高程737.7 m,坝顶处河谷宽109 m;坝底河床高程607 m,河床宽35 m,最大坝高130.7 m;堰顶高程727.0 m,设3个表孔用于堰顶溢流泄洪。大坝正常蓄水位735.0 m,相应下游水位613.0 m,淤沙高程677.7 m。坝址处多年平均气温16.6 ℃,1月多年平均气温5.7 ℃,7月多年平均气温26.9 ℃。
2.2 有限元计算模型
为准确反映坝肩岩体对大坝应力变形的影响,青龙RCC拱坝三维有限元模型模拟河谷实际地形和不同地质条件,按坝体的实际体型进行建模(如图1所示),并采用8节点6面体等参单元进行有限元离散。坝基向上、下游分别延伸200、250 m,坝基向下延伸150 m,坝肩两侧依地形均沿高程向上延伸200 m。整个计算区域内单元总数105 632个,节点总数117 081个。计算中,坝基岩体上、下游及两岸边界施加法向约束,坝基底面施加三向约束。

图1 拱坝三维有限元整体网格和坝体网格模型Fig.1 Whole three-dimensional finite element mesh and dam grid model
岩体与混凝土材料采用的本构模型为理想弹塑性模型,屈服准则为Drucker-Prager准则,其准则在π平面上是圆, Drucker-Prager准则的屈服条件如下:
(3)
式中:I1、J2分别为应力张量的第一不变量和应力偏张量的第二不变量;α、k为正的材料数。
由于计算采用的Drucker-Prager准则的屈服面是Mohr-Coulomb的外接圆锥,α、k与材料黏聚力c、内摩擦角φ换算如下:
(5)
2.3 材料物理特性
根据青龙RCC拱坝混凝土及岩石力学试验结果,确定材料参数的取值。由于不同性质的岩体的分区,坝基自上而下分别为A、B、C 3个材料区。坝体混凝土、坝基岩体材料参数如表1所示。
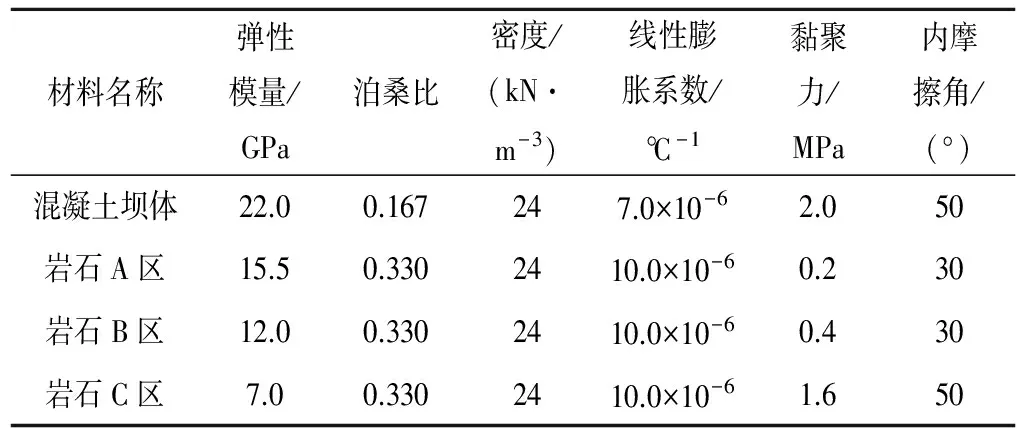
表1 坝体混凝土及坝基岩体材料力学参数Tab.1 Mechanical parameters of dam, rock mass
2.4 研究方案
本文在选取封拱温度场方案时,兼顾实际工程的施工情况以及研究需要。青龙RCC拱坝在施工过程中采用不设横缝、整体连续上升浇筑的方式,其实际封拱温度为坝体混凝土达到的最高温度,且沿厚度方向的温度分布大体对称,故认为封拱温度场中Td0≈0。封拱温度场在施工过程中经多次调整最终拟定出4种方案(如表2所示)。大体思路为:方案1~方案4的Tm0值呈梯度依次递增;方案2整体比方案1增加4 ℃;方案3在方案2的基础上将645~670高程处的Tm0增加3 ℃;方案4在方案3的基础上将680~700 m高程处的Tm0增加10.6 ℃。
根据SL282-2003《混凝土拱坝设计规范》规定的计算方法,结合工程当地的水文气象资料,计算出坝体多年年平均温度场Tm1、Td1和坝体多年平均变化温度场Tm2、Td2(见表2)。将各特征温度场的温度参数值带入式(1)、式(2),得到各个方案的温度作用Tm、Td(见表3)。
本报讯近日,中国氮肥工业协会组织召开“2018年中国氮肥、甲醇技术大会”。会上对2017年氮肥、甲醇行业取得的技术进步创新成果和节能减排先进单位进行了隆重表彰。新洋丰被授予中国“2017年度氮肥、甲醇行业节能减排先进单位”称号,这是对公司一年来在绿色循环发展方面所取得成绩的充分肯定。
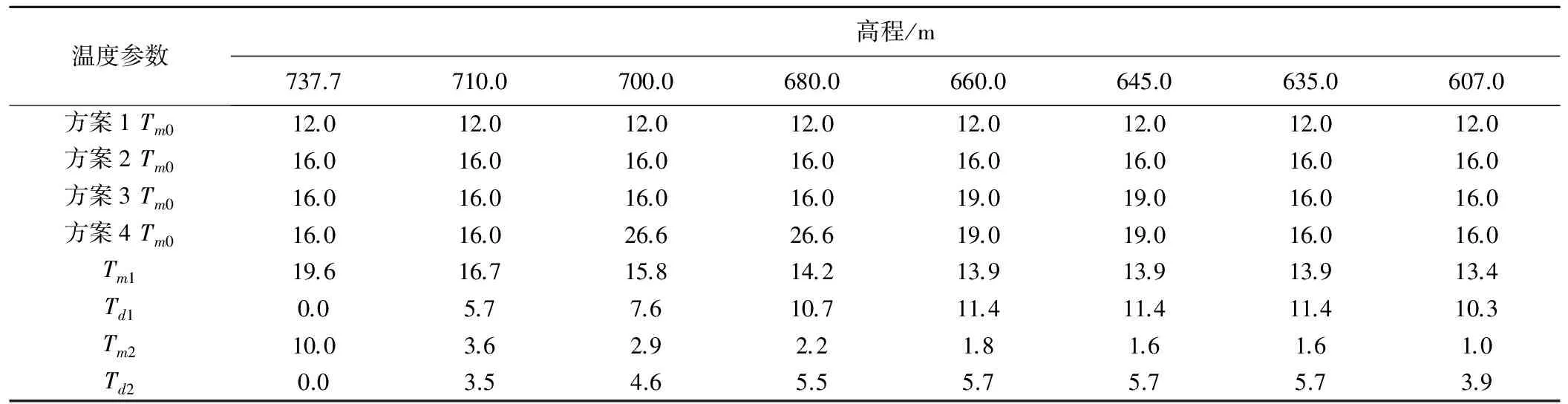
表2 特征温度场温度参数 ℃

表3 各方案坝体温度作用 ℃
2.5 荷载组合
对于RCC拱坝而言,温度作用主要发生在运行期,且温降作用是拱坝产生裂缝的主要原因,对拱坝运行安全极为不利。所以本文主要针对拱坝在正常水位运行情况下的温降工况进行计算分析。荷载组合为:自重、上、下游坝面静水压力、泥沙压力、扬压力以及温度作用。
3 各方案运行期工况变形分析
选取正常运行期温降工况分析,青龙RCC拱坝在不同封拱温度场方案下,上游面拱冠梁处顺河向位移沿高程的分布如图2所示。纵向分析:就单个方案而言,拱冠梁顺河向位移沿高程呈抛物线分布,一般以1/3、1/2坝高处位移最大。横向比较:在方案1、2、3、4中,随着温度参数Tm0逐渐增大,各方案下的拱冠梁顺河向位移除坝底以外均随之增大,其中1/2坝高处位移增大最为明显,增大程度沿高程分别向坝底和坝顶递减。综合来讲,随着封拱温度场中温度参数Tm0的增大,青龙RCC拱坝拱冠梁顺河向位移也逐渐增大。
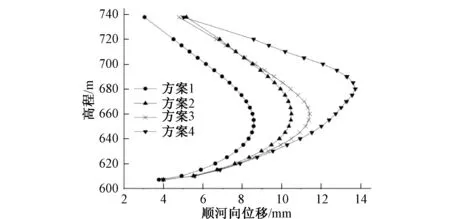
图2 运行期温降工况下拱冠梁顺河向位移Fig.2 Y-displacement at arch crown beam under operation of temperature fall condition
4 极限承载能力分析
一般采用强度储备系数法和超载法进行拱坝极限承载能力分析。强度储备系数法(亦简称降强法)即通过逐步降低材料强度,使正常工作状态的坝体达到结构破坏,其中强度储备系数Kf为材料设计强度与破坏强度的比值。超载法包括超水位法和超水容重法,即以抬高水位方式或增加水容重方式,直至坝体结构失去承载能力,其中超载系数Kp为破坏水压荷载与设计水压荷载比值,或破坏容重与设计容重的比值。很多学者认为[9],在除去基础沉陷、坝肩失稳等因素的影响外,高拱坝的破坏主要是材料强度的不足。强度储备系数法能比较真实反映结构破坏本质以及可能的破坏模式。因此,本文采用强度储备系数法进行青龙RCC拱坝极限承载能力的分析。基于正常运行期的温降工况,保证结构的正常工作状态不变,采用降低原结构材料黏聚力c和内摩擦角φ的方法,以0.2倍的折减系数逐步进行模拟。
4.1 位移分析
根据第3节的分析可知,在不同的封拱温度场下,青龙RCC拱坝上游坝面顺河向位移的最大值往往发生在拱冠梁1/2坝高和1/3坝高。本节采用位移突变法,通过对比各封拱温度场的计算结果,分析1/2坝高、1/3坝高及坝顶这3个特征位置的顺河向位移与强度储备系数的关系曲线。其演变过程均表现为:在降强的初始阶段,各方案下特征位置的顺河向位移基本稳定在某一数值即呈线性变化。随着强度储备系数的增大,在某一强度储备系数处(本文设为“稳定强度储备系数”)出现明显拐点,顺河向位移由缓慢增长阶段进入急剧增大阶段,此时,位移增量与强度折减系数增量之比△UY/△UKf开始急剧变化,最终特征位置处顺河向位移逐渐趋于水平。
各方案下拱冠梁处特征位置的“稳定强度储备系数”如表4所示。将各方案下拱冠梁坝顶处这一特征点的顺河向位移及增幅与强度储备系数关系曲线汇集如图3和图4所示。可知,封拱温度场的变化对拱坝应变有一定的影响。随着封拱温度的增大,各特征位置的“稳定强度储备系数”逐步减小,即位移演变过程线的拐点位置提前,拱坝开始进入不稳定状态时的强度储备系数降低。

表4 各方案下拱冠梁处特征位置的“稳定强度储备系数”Tab.4 “Steady strength accumulation coefficient” at typical measuring points on arch crown beam
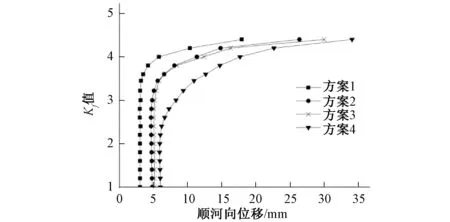
图3 各方案下拱冠梁坝顶处顺河向(Y向)位移与强度储备系数关系曲线Fig.3 Relationship between y-displacement and strength accumulation coefficient at top point on arch crown beam under each scheme

图4 各方案下拱冠梁坝顶处顺河向(Y向)位移增幅与强度储备系数关系曲线Fig.4 Relationship between ratio y-displacement amplification and strength accumulation coefficient at top point on arch crown beam under each scheme
4.2 塑性区分析
各封拱温度场方案下,青龙RCC拱坝上、下游坝面塑性区演化过程见图5~图8。文中按等效塑性应变大于10-5作为破坏标准。有别于只采用极限承载的最终成果作为安全评价的判断依据,本文考虑了在极限承载过程中拱坝由局部破坏到最终溃坝的演化过程,着重分析拱坝从局部材料层次的破坏逐渐过渡到整个结构层次的失效过程。
(1)方案1:强度储备系数Kf=1.0,即未降强时,坝体没有产生塑性破坏;在Kf=1.8时,上游坝面右岸坝踵开始出现小部位的塑性区,并逐渐沿坝基扩展;至Kf=2.4时,下游坝面塑性区沿左、右岸坝肩及底部达到线状贯通;继而Kf=3.4时,上、下游坝面溢洪道附近开始塑性屈服,坝底及左岸坝肩1/3坝高处塑性区发生成由上游面至下游面的贯通;降强终段Kf=4.2时,坝面下游大面积屈服,坝体濒临破坏边缘,但计算仍收敛。在Kf=4.4时,上、下游坝面完全破坏,建基面破坏区全部贯通,拱坝的高次超静定结构遭到破坏,且此后迭代求解不收敛,表明拱坝溃决(见图5)。

图5 方案1降强过程上、下游坝面典型等效塑性应变分布Fig.5 Plastic strain of dam body under loading process of plan A
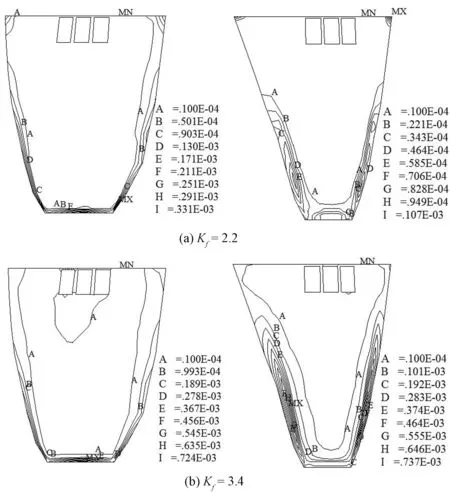
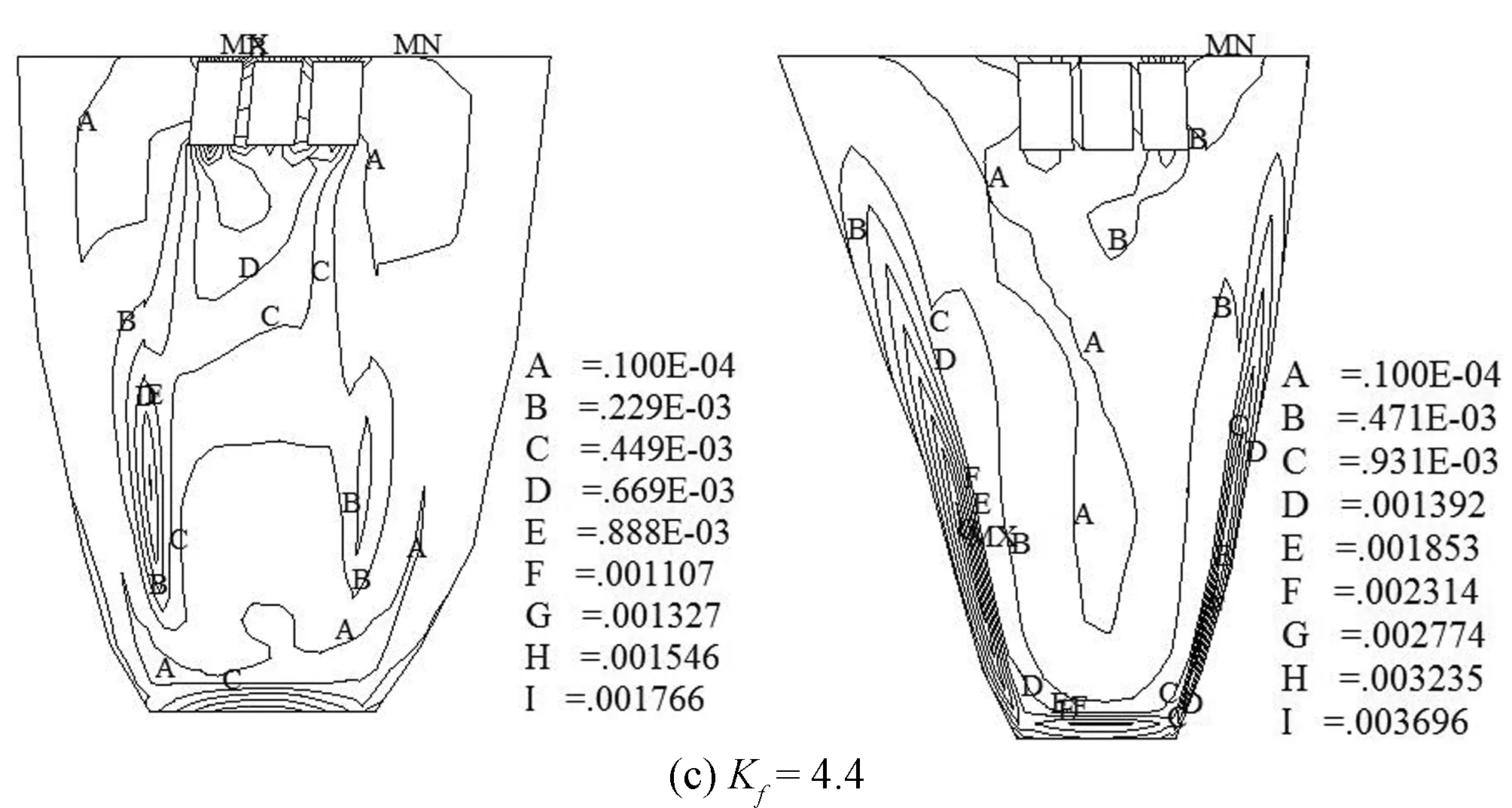
图6 方案2降强过程上、下游坝面典型等效塑性应变分布Fig.6 Plastic strain of dam body under loading process of plan B
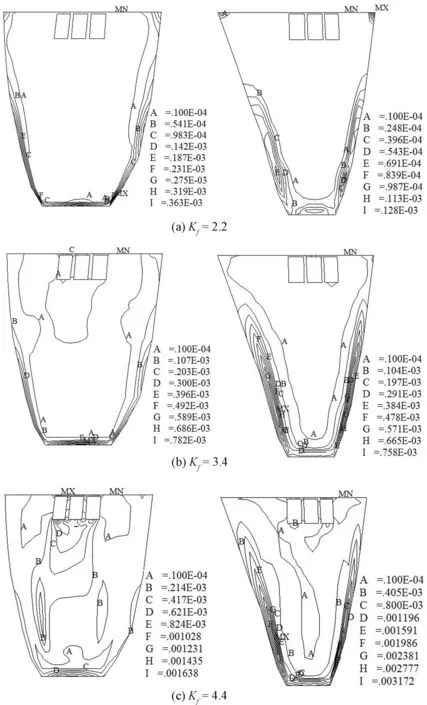
图7 方案3降强过程上、下游坝面典型等效塑性应变分布Fig.7 Plastic strain of dam body under loading process of plan C
(3)方案3:强度储备系数Kf=1.2时,即降强起始,上游坝面塑性区沿两岸坝肩至3/4坝高处形成线状贯通;至Kf=2.2时,达到完全竖向贯通。降强度中期Kf=3.4时,下游坝面破坏区沿两岸坝肩扩展成从坝底到坝顶的竖向贯通,上游坝面溢洪道底部的塑性区向下发展至1/2坝高处;Kf=3.8时,破坏区在上游坝面发生横向贯通。降强终期Kf=4.4时,坝体内部出现大范围破坏区,左右岸坝肩破坏区沿上、下游面全部贯通,此后迭代求解不收敛,认为此时拱坝不具备承载能力,已经发生破坏(见图7)。
(4)方案4:降强伊始Kf=1.2 时,上游坝面塑性区沿两岸坝肩及底部已达到“U”型联通;在Kf=2.2,下游坝面两岸坝肩破坏区联通至4/5坝高,至降强中间段Kf=2.8,下游面两岸坝肩破坏区发展成竖向贯通,且溢洪道底部及1/2坝高拱冠梁处开始出现塑性区,此后,不断向四周蔓延;Kf=3.6破坏区在上游坝面形成横向贯通;Kf=3.9时,下游坝面塑性区亦发生横向贯通;降强度末期Kf=4.2时,坝体濒临破坏边缘,建基面和上、下游坝面的绝大部分区域均已处于塑性屈服;Kf=4.4,上、下游坝面完全破坏,且此后拉格朗日迭代不收敛,拱坝高次超静定结构遭到破坏,失去承载能力(见图8)。
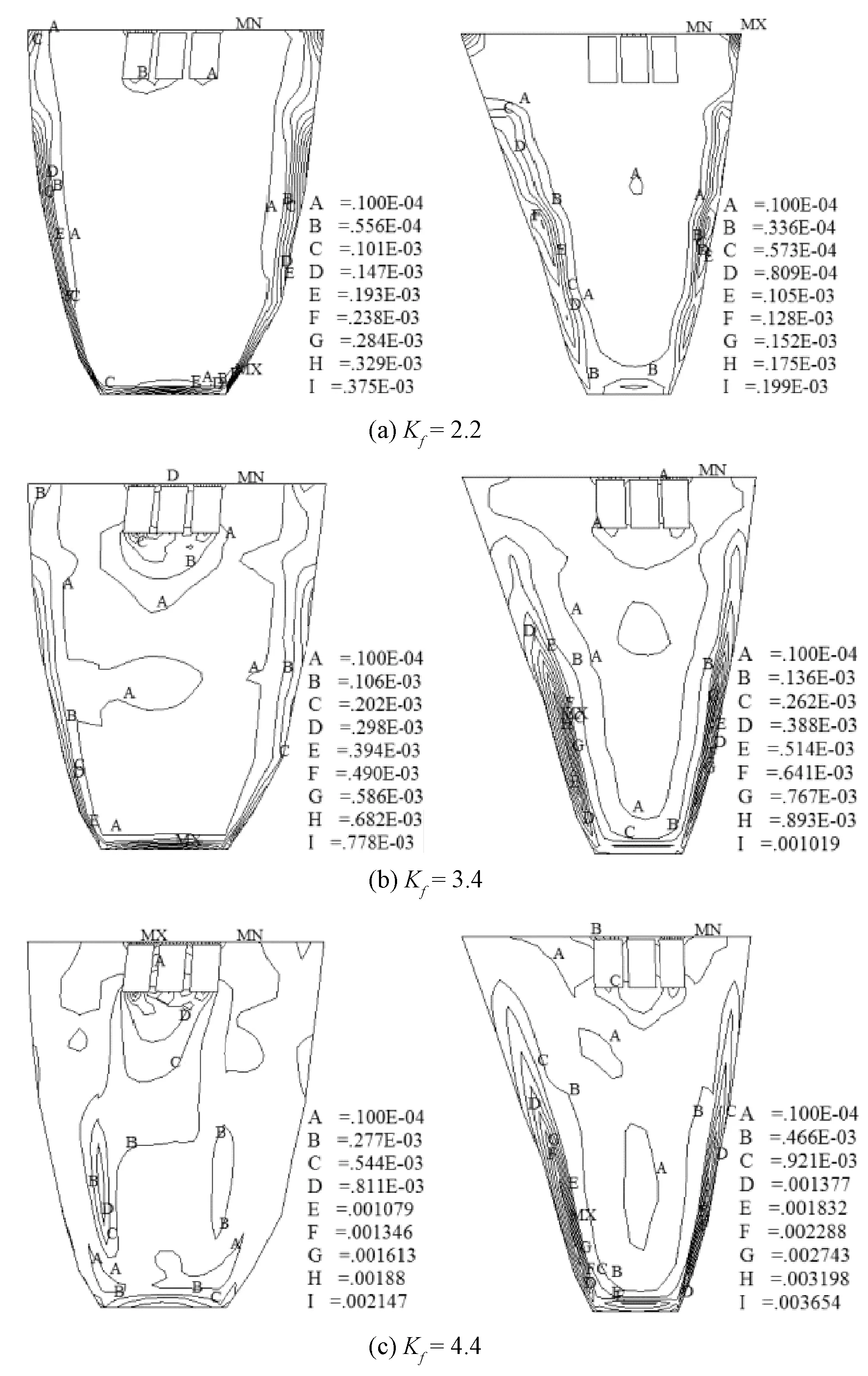
图8 方案4降强过程上、下游坝面典型等效塑性应变分布Fig.8 Plastic strain of dam body under loading process of plan D
为清晰明了的对比不同封拱温度场下青龙RCC拱坝的渐进破坏形态,依据本文采用的破坏判据,将拱坝极限承载过程中出现典型破坏状态时对应的强度储备系数列于表5。随着封拱温度的增大,同一个典型破坏状态对应的强度储备系数逐渐减小,但各方案下最终溃坝时对应的强度储备系数不变;即坝体塑性区的发展速度变快, 但坝体最终的承载能力不变。
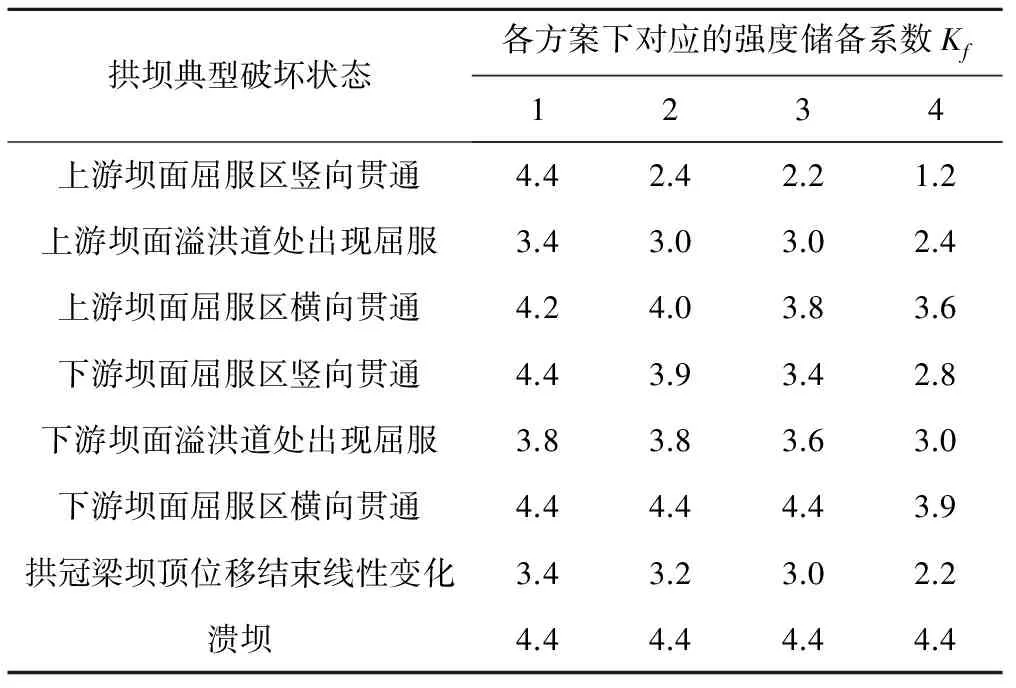
表5 各方案下拱坝出现典型破坏状态时对应的强度储备系数Tab.5 Strength reserve coefficient of each scheme under typical destruction state
5 结 语
本文从控制封拱温度场切入,采用弹塑性有限元方法,计算分析不同封拱温度场下青龙RCC拱坝在降强过程中的渐进破坏模式及强度储备系数变化规律。计算结果表明:
(1)封拱温度越高,青龙RCC拱坝在降强过程中塑性区的发展速度越快,但最终的溃坝强度储备系数基本不变,即,封拱温度场的变化对青龙RCC拱坝坝体的应力影响很大,但对其极限承载能力影响很小。
(2)随着封拱温度的增大,青龙RCC拱坝拱冠梁特征位置顺河向位移与强度储备系数关系曲线发生拐点时的强度储备系数逐步减小。即,封拱温度场的变化对青龙RCC拱坝坝体应变有一定的影响。
(3)青龙RCC拱坝在不同封拱温度场下溃坝时的强度储备系数均为Kf=4.4。
□
[1] 朱伯芳.大体积混凝土温度应力与温度控制[M]. 北京:中国电力出版社,1999.
[2] SL282-2003,混凝土拱坝设计规范[S].
[3] 张国新,杨 波,张景华.RCC 拱坝的封拱温度与温度荷载研究[J].水利学报,2011,42(7):812-818.
[4] 李守义,马 强,张晓飞.基于有限元等效应力法的高拱坝封拱温度场研究[J]. 水力发电学报,2015,34(7):88-94.
[5] 查龙青,王均星,杨舒涵,等.青龙RCC拱坝封拱温度对拉应力的影响[J].水电能源科学,2016,34(3):80-83.
[6] 赵靖伟,张 博,周邠鹏.碾压混凝土拱坝封拱温度场的仿真分析[J]. 水资源与水工程学报,2011,22(2):126-131.
[7] 黎展眉.普定碾压混凝土拱坝裂缝成因探讨[J].水力发电学报,2001,(1):96-102.
[8] 黎展眉.拱坝温度荷载与温度应力的考虑[J].水利水电科技进展,2001,25(5):9-11.
[9] 林 鹏.高拱坝超载的计算机仿真[J].水利水电技术,2000,31(8):4-7.

