U型结构中的水体振荡特性

戴 熙 武

(河海大学水利水电学院，南京 210098)

在水利工程中，存在一些类似U形管的水工建筑结构，这些结构共同的特点是在两端具有自由水面，中间由有压管道连接，本文暂且称之为U形结构。例如上游水库、中间引水管以及调压室组成的结构，上、下游双调压室及中间有压管道组成的结构[1]，分段低压输水系统中的输水单元等都是U形结构。我们知道，在反射水击波的时候，调压室中水面会产生振荡，一段时间内，调压室水面在某一静水位线上下振荡，直至由于摩阻损耗使动能不断减小才逐渐恢复平静。同样，在U形结构中，当水体中存在某种扰动时，两端自由液面会交替上升与下降，直至由于摩阻损耗慢慢恢复平静，在这一过程中其水面振荡具有某一相对固定频率。吴持恭推导出了U形管中自由液面振荡频率公式[2]，但其不适用于上、下游管道横面面积与有压管道截面积不等的情况；万五一等在U形管振荡公式基础上推导出了分段低压输水系统中U形结构的振荡频率公式[3-6]，但其精确程度较低，只能作为初步的估计。本文将对U形结构中上、下游管道横截面面积、有压管道截面积、有压管道长度对其振荡频率的影响规律进行研究，这对于U形输水结构中水面振荡及水力共振的研究具有重要意义。

1 基本理论

在盛水的等截面U形管中，由于某种外界扰动左右自由液面产生一定高差，在重力及惯性力作用下，管中水体将来回振荡，并由于摩阻力作用逐渐衰减最终达到平衡。对于等截面的U形管，利用非恒定流的能量方程可以推导出这种振荡的振幅、周期及水面位移等与时间的关系。吴持恭对U形管上、下游管道自由液面所在的两个断面应用非恒定流能量方程推导出自由液面振荡方程[2]：

(1)

(2)

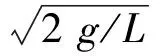
由上式可知U形管中水面振荡周期只与U形管中水柱长度有关，而与管道横截面面积无关。

万五一在U形管振荡的基础上，进行一些假设与简化，从非恒定流的运动微分方程出发推导出分段低压输水系统中的输水单元，自由液面振荡周期公式[3]：

(3)

式中：F为上游管道横截面面积；L为有压管道长度；A为中间有压管道横截面积。

该公式考虑了上游管道横截面面积对振荡所造成的影响，但由于忽略局部水头损失的因素，得到的结果准确性不高。并且该公式只适用于下游管道横截面积与中间有压管道横截面积相等的情况。

2 模型建立及计算方法

2.1 模型建立及网格划分

本文数值模拟的U形结构如图1所示，上下游竖直管道长度H=2.0 m,中间有压管道厚度d=0.1 m。由于本文进行的是二维数值模拟，建模时不考虑垂直于纸面方向尺寸，通过改变L1(L2)来体现上(下)游横截面面积F1(F2)的改变，L1(L2)与d的比值即为F1(F2)与中间有压管道横截面面积A的比值。网格划分采用结构化网格，网格间距为0.01 m，划分结果如图2所示。

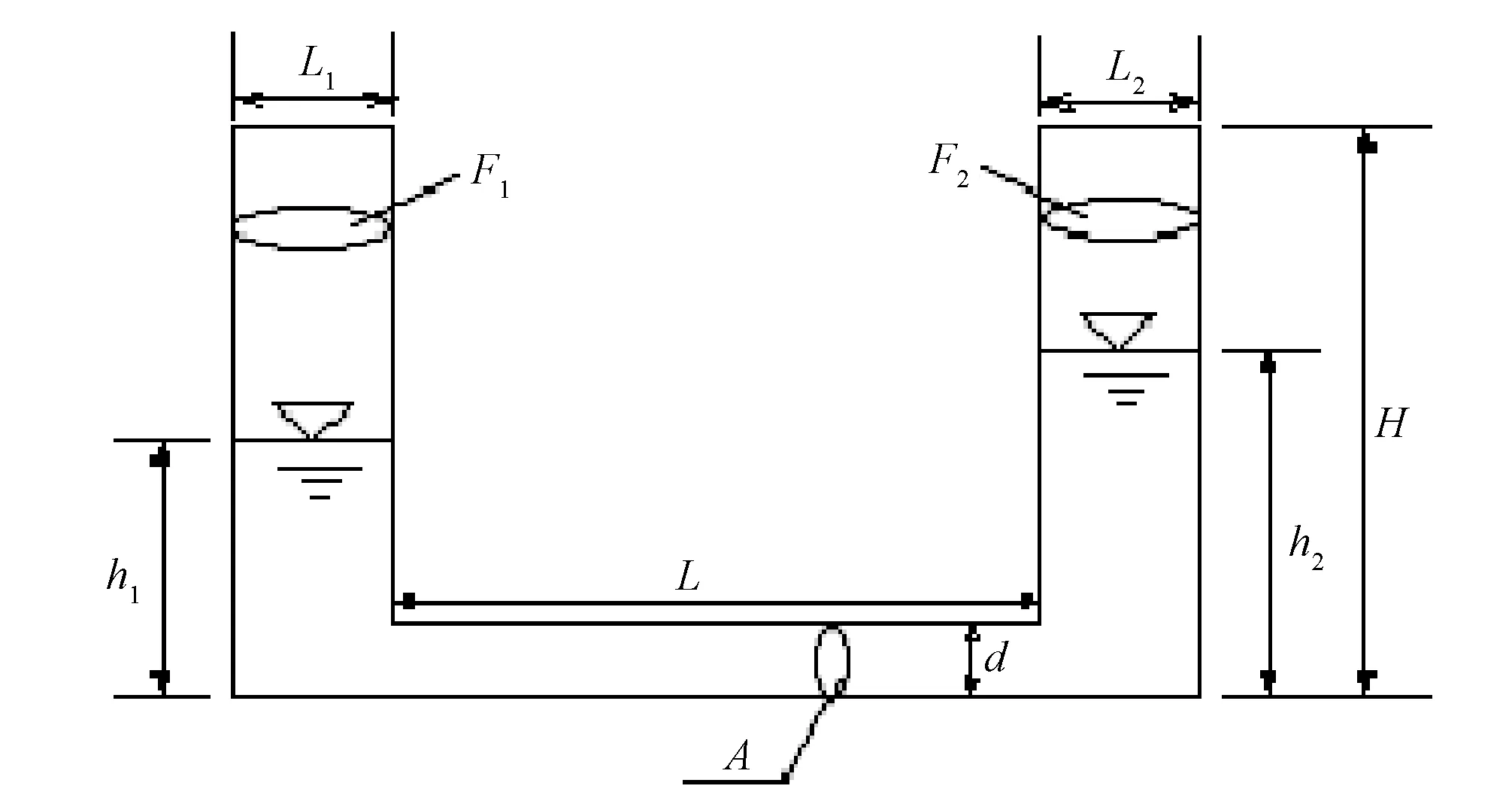
图1 U形结构示意图Fig.1 Schematic diagram of U-type structure

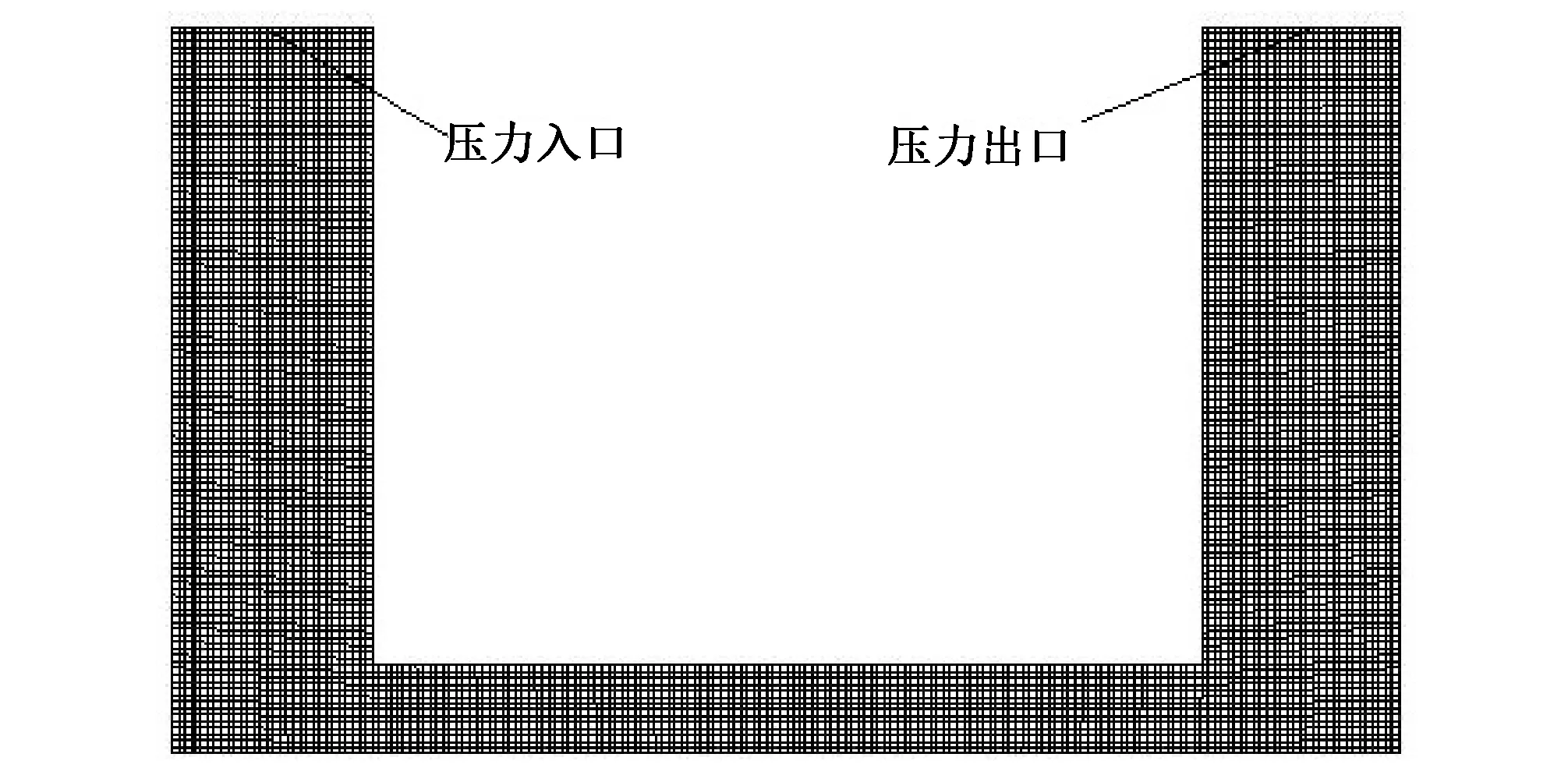
图2 模型网格划分Fig.2 Model mesh generation

2.2 计算方法及边界条件

本文采用Realizablek-ε紊流模型进行非定常流数值模拟，具体的控制方程详见参考文献[7,8]，k和ε的输运方程中C2=1.9、σk=1.0、σε=1.2，其他系数按参考文献[8]确定。采用有限体积法对控制方程进行空间离散，使用PISO算法进行压力与速度的耦合，并且考虑重力的影响。由于上下游涉及水气两相流，采用VOF模型来对自由液面进行追踪，为了更精确地得到水气分界面，采用显示格式进行模拟。

U形结构上游进口边界为压力入口边界，P1=0；下游出口边界为压力出口边界，P2=0；其余为固体边壁，采用考虑壁面粗糙影响的壁面函数来处理。初始化条件为上游管道中水深h1=1.0 m,下游管道水深h2=1.2 m，从而使左右两侧液面来回晃动。

3 模型验证

鉴于试验条件有限，本文采用吴持恭推导出的理论公式即本文中公式(2)验证本文数值模拟结果的可靠性。验证模型为管径D=0.1 m的U形管，U形管验证模型的计算方法及边界条件等与U形结构模型一样。将数值模拟得到的U形管液面振荡周期与理论公式(2)计算结果进行对比与验证；同时将F1=F2=A=0.1 m×0.1 m的U形结构的数值模拟计算得到的振荡周期与U形管振荡周期进行对比，如表1所示。

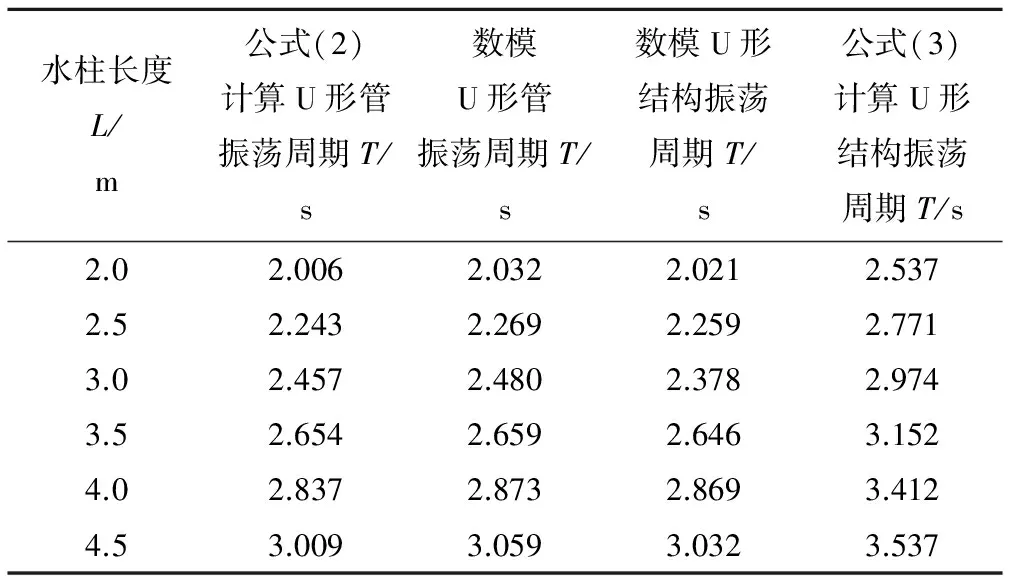
表1 振荡周期数据表Tab.1 Statistics of oscillation period

由表1可知，U形管模型在各水柱长度下由公式(2)计算得振荡周期与数值模拟的结果十分吻合，误差约为1.4%，说明本文采用的数值模拟方法得到的结果具有较高的可靠性；在水柱长度相同时，U形管与U形结构数值模拟得到的振荡周期基本一致，所以等截面的U形结构(F1=F2=A)的水面振荡周期可用公式(2)来近似计算；由公式(3)计算得到的U形结构振荡周期与数值模拟得到的周期差异较大，约为17%左右，说明当水柱长度较短时，用公式(3)计算振荡周期将产生较大的误差，这是由于忽略弯管处局部水头损失所引起的，因此有必要探索U形结构弯管处水流流态对水体振荡所带来的影响。

4 计算结果及分析

4.1 上、下游截面面积对液面振荡周期的影响

首先，保持F2=A，在中间有压管长度分别为L=4、14、40、200、1 000、2 000 m时，使F1分别为有压管道截面积A的n倍(1、2、4、6、8、12、16、20)，数值模拟得到U形结构的水面振荡周期T。由公式(2)计算具有等长有压管的等截面(F1=F2=A)U形结构的水面振荡周期T0，引入一个周期修正系数α，使α=T/T0,α反映了上下游侧管道横截面面积及中间有压管道长度对振荡周期的影响，得到修正系数α与面积倍数n的关系曲线如图3所示。

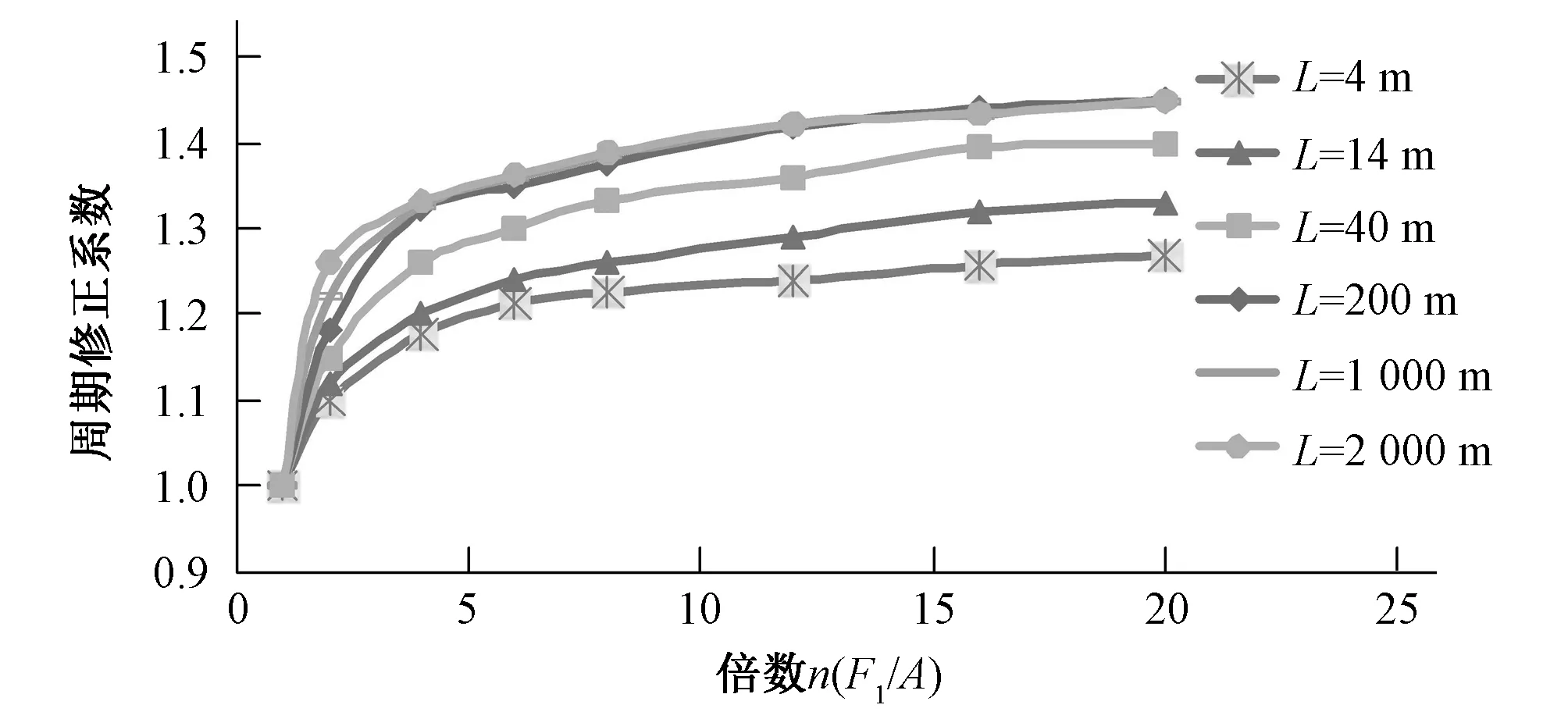
图3 周期修正系数与面积倍数n关系曲线Fig.3 Relationship curve between period correction factor and area ratio n

然后同时改变上游与下游侧管道横截面面积，但保持F1=F2，同样得到修正系数α与面积倍数N的关系曲线如图4所示。

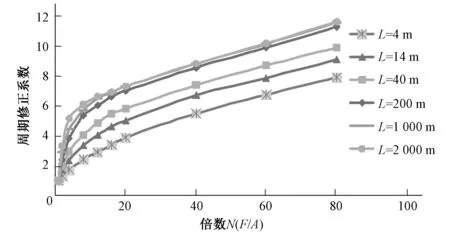
图4 周期修正系数与面积倍数N关系曲线Fig.4 Relationship curve between period correction factor and area ratio N

由图3可知，修正系数α与面积倍数n的关系曲线大致呈现对数分布，曲线随面积倍数n增大逐渐上升，但上升幅度逐渐减小，最后曲线趋于平缓，并且L=200 m，L=1 000 m,L=2 000 m 3条曲线基本重合。由此可知，上游侧横截面积F1及管道长度L均会影响周期修正系数α。随着上游侧横截面积F1的增大，周期修正系数α逐渐增大，但增幅慢慢减小。当上游侧横截面积F1一致时，有压管道长度L越长，周期修正系数α越大，但当管道增长到200 m以后，修正系数基本一致，由此可知中间有压管道长度只在一定范围内才对周期修正系数有影响，因此本例中当中间管道长度达到200 m以后可以拟合出公式α=0.082 ln(n)+1.21。从而的到振荡周期的公式:

(4)

式中：F1为上游侧管道横截面面积；A为中间有压管道横截面积；L为中间有压管道长度。

由图4可知修正系数α与面积倍数N的关系曲线在N小于10时上升很快，然后上升速度逐渐减慢，当N大于20以后呈现为一条斜线，随面积倍数N增大逐渐上升，L=1 000 m,L=2 000 m 2条曲线基本重合。对比图5可知，同时改变上下游侧横截面积对振荡周期带来的影响比该变一侧横截面积大很多，改变一侧面积当倍数n达到10倍以后周期修正系数α增长很慢，但改变两侧面积时，即使倍数N达到60～80，周期修正系数α增长还较大，说明两侧面积对振荡周期带来的影响并不是简单地叠加。但当管道增长到1 000 m以后，修正系数基本一致，也说明两侧面积对振荡周期的影响很大。

4.2 上、下游截面面积对液面振荡幅度的影响

由于壁面摩阻及空气摩阻等原因，U形结构的振荡随着时间慢慢衰减，最后两边的自由液面恢复平静。为了探究上、下游横截面积对U形结构水面振荡幅值影响，假设水面波动前一时刻Ti振幅为Ai，经过一个周期后的Ti+1时刻振幅为Ai+1，衰减系数Gi=Ai+1/Ai,做出Gi与i(i=1,2,3,4,5,6,7,8,9)之间的关系曲线，如图5所示。

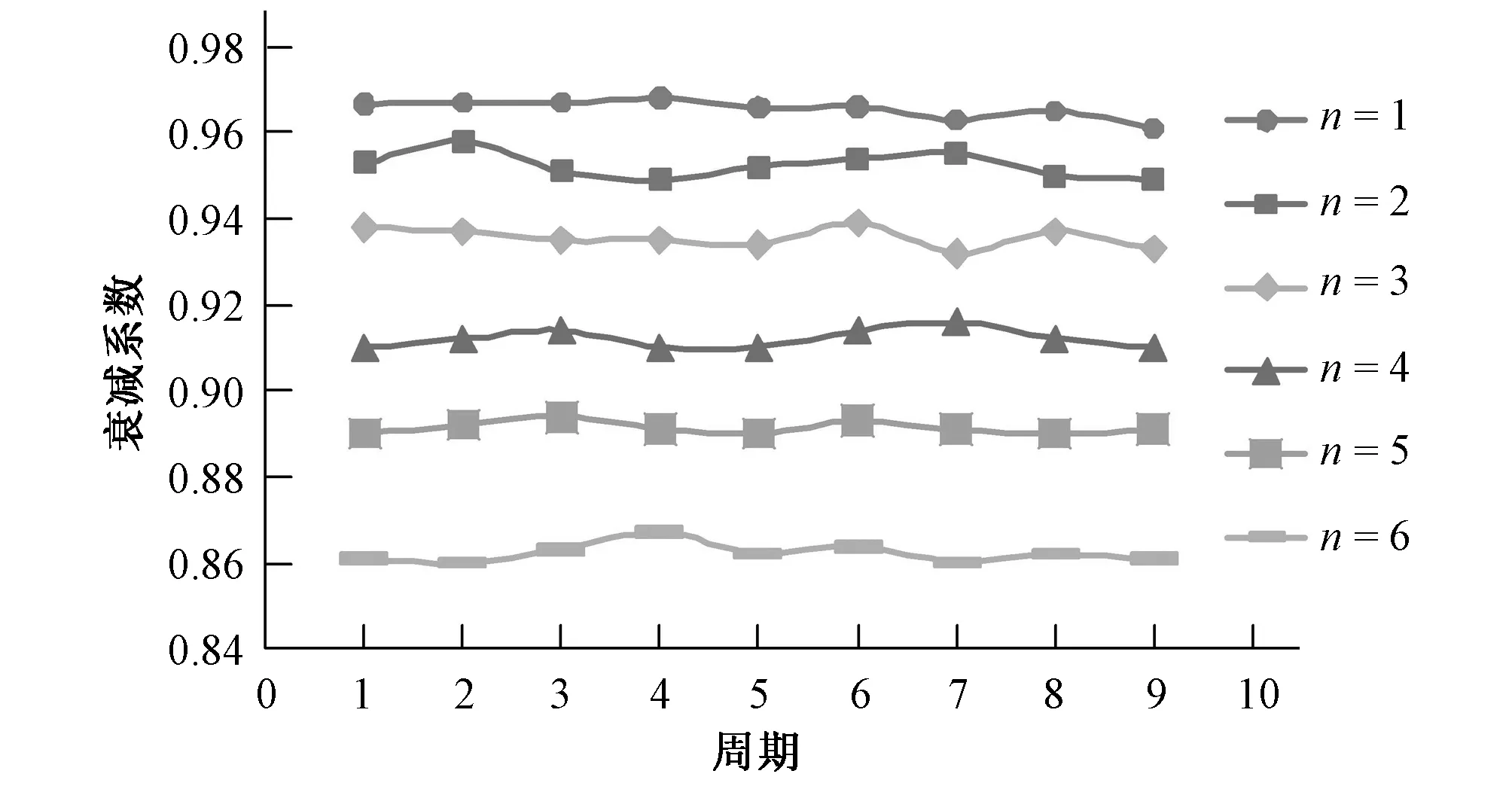
图5 衰减系数Gi与i之间的关系曲线Fig.5 Relationship curve between attenuation factor Gi and i

由图5可知，当只改变上游侧横截面面积使F1=nA，n=1,2,3,4,5,6时，各条曲线Gi随i的变化很小，说明体型一定时U形结构水面振荡的衰减率基本一定；并且倍数n越大，Gi越小，说明上游横截面面积越大，水面振荡越快衰减，水面能更快恢复平稳。

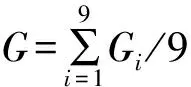
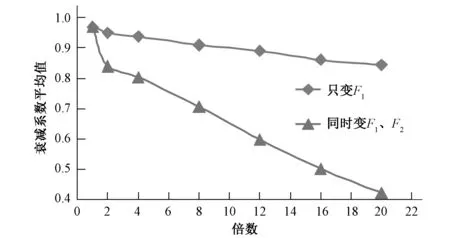
图6 衰减系数平均值G与面积之间的关系曲线Fig.6 Relationship curve between average attenuation factor G and the area

由图6可知，只改变上游侧横截面积F1为有压管截面积A的n倍时，曲线逐渐下降；同时改变上下游横截面积使F1=F2=NA时，曲线较只变上游侧面积的曲线下降更快。由此可知，增大上(下)游侧横截面积能加快U形结构水面振荡的衰减，并且同时增大上下游横截面面积能更加显著地减小衰减系数，能使水面更快恢复平静。

4.3 改变上、下游截面面积对振荡过程中水流流态的影响

以下分别为等截面U形结构F1=F2=A；只改变上游侧管道横截面面积使F1=10A；同时改变上下游侧管道横截面面积使F1=F2=8A时，U形结构水面振荡过程中，上、下游侧局部位置的水流流线图(见图7～图9)。

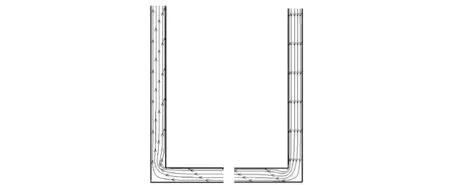
图7 F1=F2=A时流线图Fig.7 Streamlines of Local region under F1=F2=A

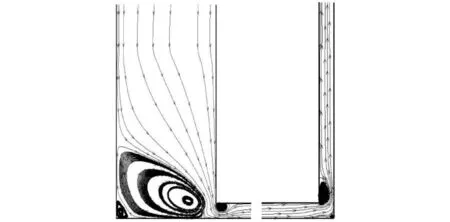
图8 F1=10 A时流线图Fig.8 Streamlines of Local region under F1=10 A

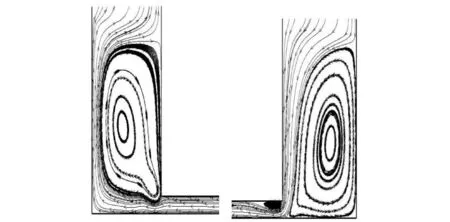
图9 F1=F2=8 A时流线图Fig.9 Streamlines of Local region under F1=F-2=8 A

由图7可知，当上下游横截面与中间有压管道截面积相同时，振荡过程中水流流线比较顺直，只在管道转弯处流线较弯曲，从而其局部水头损失系数较小，水面振荡衰减较慢。由图8可知，当上游侧管道横截面积比中间有压管横截面积大较多时，振荡过程中在上游侧存在一个较大的漩涡，进入有压管道时流线较弯曲，故在此处局部水头损失较大，并且在下游侧与有压管道衔接处有一个相对于管径而言较大的漩涡，严重挤压主流流线，此处水头损失也较大，从而造成水面振荡较快衰减。由图9可知，当同时增大上下游侧横截面积时，在上下游侧均存在一个较大的水流漩涡，主流流线也较弯曲且严重受到水流漩涡的影响与压迫，在下游侧与有压管道衔接处也存在一个较小的水流旋滚，故而同时增大上下游侧面积使水流流态进一步恶化，能很快达到消能的目的，水面振荡能很快衰减。

5 结 语

(1)采用二维数值模拟的方法能较好的模拟U形结构水面振荡的过程，数值模拟得到的U形管的振荡周期与吴持恭推导的公式计算的振荡频率基本相同；数值模拟等截面的U形结构与U形管得到的振荡周期相差无几，故等截面的U形结构可用U形管周期的计算公式来计算振荡周期。

(2)增大上(下)游侧管道横截面面积会使水体振荡周期增大，但其增加效果慢慢减小；同时增加上、下游侧管道横截面面积能较显著使水体振荡周期增大；增加有压管道长度使之达到一定长度以后，上下游侧管道横截面面积对于振荡周期的影响趋于一致。

(3)当U形结构体型一定时，其水面振荡振幅的衰减速度几乎为一个定值；增大上(下)游侧横截面积能加快水面振荡的衰减，同时增大上、下游侧横截面积较只改变上(下)游侧横截面积能更显著加快水面振荡的衰减。

(4)等截面积的U形结构振荡过程中水流流线较顺直，当增加上(下)游侧横截面积后，会产生较大的水流漩涡，严重压迫主流，主流流线较弯曲，并且在有压管道的某些部位也会产生水流漩涡，水流流态较差，增大局部水头损失。

□

[1] 刘 畅，程永光.长连接管和分流调压室的波动稳定和衰减特性[J].水电能源科学，2012，30(2)：131-135.

[2] 吴持恭.水力学[M].北京：高等教育出版社，2005.

[3] 万五一，练继建，崔广涛.分段低压输水管系的水力振荡特性[J].水利学报，2003，(12)：34-39.

[4] 穆祥鹏，练继建，李 琳.基于水力控制的分段低压输水系统优化研究[J].四川大学学报(工程科学版)，2008，40(1)：58-63.

[5] 练继建，郑 政，李 琳，等.多孔并联分段低压输水系统的水力特性和控制[J].水利学报，2006，37(8)：950-957.

[6] 徐进超，蔡付林，周建旭.低压输水单元水力振荡的数值研究[J].水力发电学报，2012，31(2)：128-132.

[7] 王福军.计算流体动力学分析[M].北京：清华大学出版社，2004.

[8] 李家星，赵振兴.水力学[M].南京：河海大学出版社，2005.