基于云模型的水资源管理综合评价方法——以惠州市为例

苏阳悦，纪昌明，张验科，李荣波

(1.华北电力大学可再生能源学院，北京 102206；2.长江勘测规划设计研究有限责任公司水利规划研究院，武汉 430010)

0 引 言

随着经济社会的快速发展，水资源短缺的问题日益突出，已经成为制约我国经济社会稳定发展的瓶颈，采用一套行之有效的水资源管理办法就显得尤为重要。在2011年中央一号文中对新时期水资源管理给出了新的定义，并由此产生了新的管理指标体系，众多学者在这方面已做出了有益的尝试，并取得了一定的成果[1-3]。然而水资源管理评价标准的明确界定存在一定的难度，在指标的选取与权重确定上存在不确定性与模糊性，导致评价结果在某种程度上造成一定的差异，呈现出来的评价状态值也会有所不同，甚至出现不同评价方法的评价结果缺乏一致性。目前常用的评价方法有模糊评价法、人工神经网络等综合评价方法[4-7]，这些评价方法对一些量化困难、只能定性描述的事件具有良好的处理效果，但评价结果的信息量却较为单调。当前最严格水资源管理制度的评价方法仍在探索之中，方法局限在专家调查法(Delphi)、层次分析法(AHP)等，存在较大的主观性。

本文创新点在于将云模型理论[6,7]应用在新时期的最严格水资源管理评价中，试图建立基于云模型与模糊综合评价法的改进评价模型，除了可以实现定性概念和定量数值之间的不确定性转换，体现语言概念的随机性与模糊性，还能反映评价体系里的层次关系，并给出评价结果的信任度与稳定度[11,12]，在一定程度上克服现有定性评价存在主观性和随意性大的缺点，能够对评价客体进行有效评价，给决策者提供了更多的有效信息，使得评价结果更加合理可靠。以惠州市为例，进行水资源管理评价实例研究，通过对比，验证该模型评价结果的可靠性、稳定性和有效性。

1 云模型理论

1.1 云模型的概念

云数字特征和云发生器是云模型理论的两个核心内容[7]。

设U是一个用数值表示的定量论域，C是U上的定性概念，若定量数值x,x∈U是定性概念C的一次随机实现，x对C的确定度μ(x)∈[0,1]是有稳定倾向的随机数，即：

μ：U→[0,1],∀x∈U,x→μ(x)

(1)

则x在论域U上的分布称为云模型，简称云，记为C(x)；每一个x称为一个云滴。

图1 正态云及数字特征

云模型用期望Ex、熵En和超熵He三个数字特征来整体表征一个概念，Ex是云滴在论域空间分布的中心值，是最能够代表定性概念的点；En是定性概念不确定性的量度，由概念的随机性和模糊性共同决定，不仅反映了云滴的离散程度，也反映了定性概念的模糊性；He是熵的不确定性量度，即熵的熵，由熵的随机性和模糊性共同决定，主要反映定性概念中不确定性的凝聚性。

1.2 云发生器

发生器是云模型中定性概念与定量数据之间相互转换的特定算法，正向云发生器实现从定性概念到定量数值的转换，由云的数字特征(Ex,En,He)产生云滴；逆向云发生器实现从定量数值到定性概念的转换，将精确的数据转换为以云数字特征(Ex,En,He)表示的定性概念。

2 基于云模型与模糊综合评价法的改进评价模型

水资源管理评价中的评价指标可以看作是数据挖掘的产物，在大量的、有噪声的、不完全的、模糊的数据中，提取出其中隐含的有用的信息，为决策者提供信息管理与决策支持[14]。

在评价模型建立中，依据人的语言习惯将评语集分为“好”“较好”“一般”“较差”“差”，这类的定性语言概念是模糊的，在度的把握上难以界定[10]。因此，用模糊数学的方法，把定性概念量化，进行模糊评价。在模糊综合评价模型中，将评价指标划分为层次结构，以权重为纽带对评价指标的隶属度进行矩运算，并按一定的评价准则得到评价结果，这提供了更多的信息，并理清了各层次间的关系[4-6]。但模糊综合评价法得到的是明确的隶属关系，并不能有效的对数据的可信度与稳定性进行很好的描述。为解决这个问题，引入云模型与模糊综合评价相结合，因为云模型可以较好的刻画随机性与模糊性两者之间的关系，对应的把信任度与稳定性[12,13]的概念引入到评价结果中，以图形直观的形式展现出来，实现评价状态集与评价指标集之间的不确定性映射。在模型权重选择上，为了减少人为打分带来的不确定性，选用熵权来确定各指标的权重[5,16,17]。

因此，将云模型、熵权法与层次模糊综合评价模型相结合以构建评价模型。

2.1 基本模型与评价指标体系构建

设评价指标集U={u1,u2,…,un}，评价状态集V={v1,v2,…,vn}。

基于云模型的多层次模糊综合评价模型可表示为：

B=A∘R

(2)

式中：B为从评价指标集U到评价状态集V的模糊关系矩阵；A为评价指标权重集；R为隶属云组成的评价矩阵。

2.2 云生成与隶属度的计算

依据云模型的理念，用概念的方法把握量的不确定性，比数学表达更真实、更具备普遍性。

首先，依据隶属度的确定方法，将已归一化处理的各评价指标后的点作为输入点，并以各输入点作为中心值生成一组具有稳定倾向的随机数。

其次，利用逆向云模型将各组随机数作为云滴，也即是输入点。并以无需确定度信息的逆向云算法得出，

(5)

得到个数字特征之后，基于云模型的综合评价法，采用云模型代替隶属函数来计算相应的评价矩阵R。

(6)

得出评价矩阵R后利用综合模糊算子，计算出综合评价结果B。

最后，得出的评价结果将会以B(Ex，En，He)的形式表现，再利用正向云发生器，将该结果生成云图，我们称之为评价对象云。

Ex表示了水资源管理评价的实际状况；En值越小表示评价结果可信度越高；He值越小表明结果的稳定性越好。

2.3 评价状态集的确定

第一步，根据已有成果，将水资源管理的评价指标属性划分为5个评价等级，即：V={V1,V2,V3,V4,V5}={差，较差，中等，较好，非常好}。

从人的主观角度出发，评价等级的取值范围并不是相等的，对于“好”“中等”“差”的概念认知相对精确，取值应当相对窄。而对于“较好”“较差”的概念认知较为模糊，故取值范围应当相对于广一些。

故本文利用模糊逻辑概念按照黄金分割法[20]，在论域[0,1]范围内，划定评价等级的评判区间。以中心点0.5作为评价等级“中等”的期望值，且Ex1=0，Ex5=1，分别为评价等级“差”与“好”的期望。评价等级“较好”与“较差”的期望值应以靠近评价等级“中等”为原则。故有Ex2=0.309，Ex4=0.691，分别为评价等级“较差”与“较好”。

这里根据经验，设He=0.01，利用正态云的性质可计算出各评价等级的云数字特征En的值；其计算公式可表述为：

Enn=(Exn+1-Exn)/3

(7)

依据云滴群对概念的贡献程度[8-11]，对于论域U中的定性概念由贡献的云滴，主要落在区间[Ex-3En,Ex+3En]，因此可以忽略该区间之外的云滴对定性概念A的贡献，也称之为“3En规则”，详细指标值见表1；各评价等级对应的评价云图，见图2。

表1 各评价等级云的数字特征及取值范围

图2 标准评价云图

实际上因各数据都归一化在[0,1]内，故图表所示的云数字特征可以表征不同评价等级，所以也可以称之为“标准评价云”。

2.4 评价准则

(8)

利用该公式计算出评价对象云与各评价标准云的相似度，根据最大相似度原则，找出与评价标准云最为相近的评价标准子云，其所对应的评价等级即为水资源管理评价等级。

2.5 模型求解流程

为模型求解流程图见图3。

图3 模型求解流程图

3 惠州市水资源管理等级评估

惠州市地处珠江三角洲东缘，北部是丘陵山地，南临南海为冲积平原，具有明显的季风环流特征，属于亚热带季风气候，秋季常受台风影响，降水量迅猛增加。惠州市分属东江下游、东江三角洲惠州、粤东沿海诸小河3个水资源四级区，水资源计算总面积为11 173 m2，行政分区为，惠城区、惠阳区、惠东县、博罗县、龙门县、大亚湾开发区、仲恺高新区7个县(区)。

惠州市水汽充沛，降雨量较为丰富，多年平均降水量1 897.0 mm，但时空分布不均，汛期为4-9月，降水量约占全年75%，10-12月和次年1-3月降水量约占全年25%。

降水量区域分布不均，西枝江流域、粤东诸河偏少，东江三角洲区偏多。全市水资源总量为125.68 m3。大中型水库蓄水总量8.77 亿m3。并且有新丰江、枫树坝、白盆珠水库实施水量联合调度。各行业需水要求基本满足。用水量中以农业用水为主，工业用水和生活用水次之。废水排放以工业和建筑业废水占七成。水质监测评价总河长556 km，其中水质为2～3类河长471 km，占84.7%。(数据主要来源于《广东省统计年鉴2015》、《惠州市水资源公报 - 2015》。)

3.1 评价指标体系构建

以资料的可获取性、指标可量化性、科学性、主导因素突出性为指标选取的原则，并参照中央一号文件的工作指导精神[1,2]，构建了惠州市水资源管理评价指标体系。

评价指标体系的构建与各个地区本身的特点直接相关，因此不同的评价指标体系并不完全相同。作为示例，图4构建了一个一般意义下的区域多层次评价指标体系。

3.2 指标隶属云计算

根据建立的惠州市水资源管理评价指标体系计算出各指标的权重与隶属云见表2。

按照熵权法可以得出熵权、熵值的计算结果，从表2可知权重分别为(0.35,0.3,0.35)，通过拟合运算规则乘法运算获得各指标对准则指标的评价贡献，再将结果通过拟合运算规则加法运算和B=A·R得到对应上级指标的综合评价云，于是水资源开发利用B1指标的隶属云为C(0.568 6,0.036 2,0.013 9)；用水效率B2的隶属云C(0.827 4,0.052 6,0.020 2)；水功能区B3(0.579 3,0.036 8,0.014 2)。

再依据子目标与权重可计算出，水资源管理指标体系A的隶属云为C(0.650 1，0.041 3，0.015 9)。

3.3 评价云图与数字特征

依据上述计算得到评价指标用水效率、水功能区、水资源开发利用的隶属云，可绘制其诊断状态云图。将其与评价状态云图进行叠加，如图4所示，就可以对用水效率的状态做出评价，直观的看图可知“用水效率”的状态云图位于标准评价云图中的“较好”与“非常好”之间，且略微向“较好”偏移，因此通过目测可以认为惠州市的用水效率的评估状态位于“较好”与“非常好”之间，且偏向“较好”。

图4 惠州市水资源管理评价体系

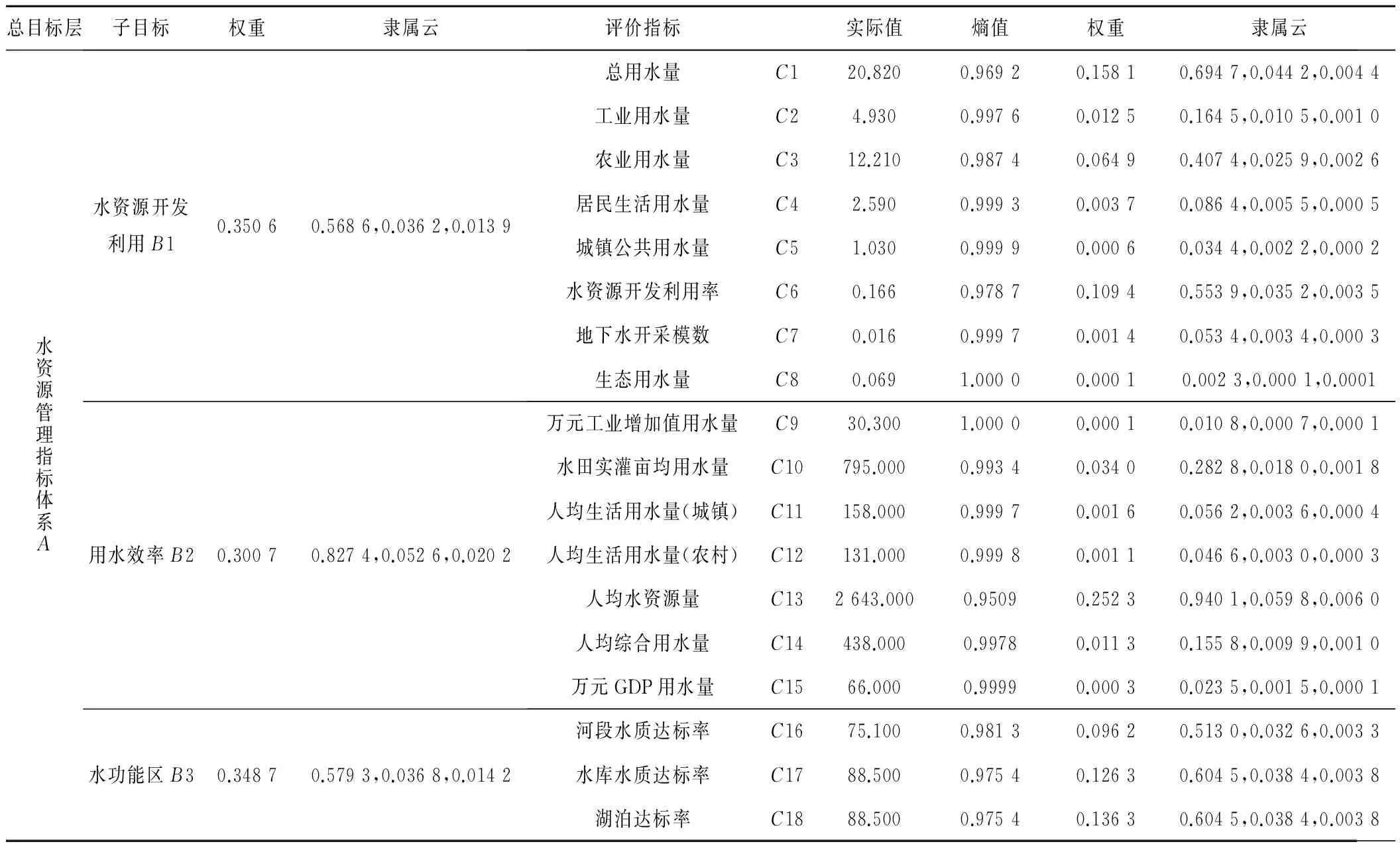
总目标层子目标权重隶属云评价指标实际值熵值权重隶属云水资源管理指标体系A水资源开发利用B10.35060.5686,0.0362,0.0139总用水量C120.8200.96920.15810.6947,0.0442,0.0044工业用水量C24.9300.99760.01250.1645,0.0105,0.0010农业用水量C312.2100.98740.06490.4074,0.0259,0.0026居民生活用水量C42.5900.99930.00370.0864,0.0055,0.0005城镇公共用水量C51.0300.99990.00060.0344,0.0022,0.0002水资源开发利用率C60.1660.97870.10940.5539,0.0352,0.0035地下水开采模数C70.0160.99970.00140.0534,0.0034,0.0003生态用水量C80.0691.00000.00010.0023,0.0001,0.0001用水效率B20.30070.8274,0.0526,0.0202万元工业增加值用水量C930.3001.00000.00010.0108,0.0007,0.0001水田实灌亩均用水量C10795.0000.99340.03400.2828,0.0180,0.0018人均生活用水量(城镇)C11158.0000.99970.00160.0562,0.0036,0.0004人均生活用水量(农村)C12131.0000.99980.00110.0466,0.0030,0.0003人均水资源量C132643.0000.95090.25230.9401,0.0598,0.0060人均综合用水量C14438.0000.99780.01130.1558,0.0099,0.0010万元GDP用水量C1566.0000.99990.00030.0235,0.0015,0.0001水功能区B30.34870.5793,0.0368,0.0142河段水质达标率C1675.1000.98130.09620.5130,0.0326,0.0033水库水质达标率C1788.5000.97540.12630.6045,0.0384,0.0038湖泊达标率C1888.5000.97540.13630.6045,0.0384,0.0038

同理，如图5与图6，也可以得出水功能区纳污方面，其评估状态位于“中等”与“较好”之间，且偏向于“中等”；而水资源开发利用上，其评估状态位于“中等”与“较好”之间，且偏向于“中等”。

最后，如图7，可以看出惠州市水资源管理总体评价，其评估状态位于“中等”与“较好”之间，且十分的靠近评价等级“较好”。

图5 水资源开发利用评价云图

图6 用水效率评价云图

图7 水功能区评价云图

图8 惠州市水资源管理总体评价云图

云用Ex、En和He这3个数字特征来整体表征一个概念，从物理意义上看Ex反应指标实际水资源管理状态的预期；En反映评价结果的可信度的一种反应，通过表2可知，“用水效率”的En=0.052 6，“水资源开发利用”的En=0.036 2，“水功能评价”的En=0.036 8，“总体评价”的En=0.041 3，数值较小，表明本次评估结果的可信度较高；He反映对不确定性评价结果带来的不稳定性的一种描述，由表2可知，“用水效率”的He=0.020 2，“水资源开发利用”的He=0.013 9，“水功能评价”的He=0.014 2，“总体评价”的He=0.015 9，数值也较小，表明本次评价结果的稳定性高。

3.4 云相似度

前文2.4已分别计算评价隶属云与各个评价等级隶属云之间的云相似度，如表3所示。该结果为惠州市水资源管理总体评价的结果，根据最大相似原则，惠州市水资源管理评估等级为“中等”。然而，通云过相似度一栏的数值不难发现，评价等级“好”“较好”“中等”数值之间的差距十分小，因此，结合图8，再次表明结果具有一致性。

表3 惠州市水资源管理评估等级云相似度计算结果

4 方法对比与分析

为了检验基于云模型的模糊综合评判方法计算的准确性，本文采用了模糊综合评判法与传统云模型对研究结果进行检验。

图9 云模型加权与云模型的模糊综合评价方法的对比云图

如表4所示，利用云模型计算惠州市水资源管理指标的云向量为C(0.700 7,0.098 2,0.051 3)。

由表5，依据最大云相似度原理，可知惠州市水资源管理水平属于“较好”的等级。这与本文最终评价结果有所差异。

导致差异的主要原因，如图9所示，通过对比可以直观地看出基于云模型的模糊综合评价法更为可信与稳定。如表4所示，从数字特征上观察，单纯利用云模型加权的方式算得的期望值，Ex=0.700 7，而云综合方法的期望值，Ex=0.650 1，两者都位于评价等级“较好”附近，但是云模型加权的熵值，En=0.982，云综合方法的熵值，En=0.041 3，可以看出本文介绍的方法熵值较小，其离散程度较小，表明本文介绍方法的信任度更高。同时，单纯使用云模型的超熵，He=0.051 3，云综合方法的超熵，He=0.015 9，本文介绍的方法的超熵值明显更小，这表明该评价结果的稳定性也更高。

表4 云模型加权算法与云模型模糊综合评价法的数字特征

表5 云模型加权算法的云相似度计算结果

综合评判的计算结果，如表6所示，可知利用模糊综合评判法计算的惠州市水资源管理等级隶属度，根据最大隶属度最大原则，判定水资源管理水平属于“较好”的等级。同时利用Mamdani模糊控制方法，可以计算出惠州市管理等级的程度为0.69，而基于云模型的综合评价法的等级程度则为0.65，相差值为0.04，评判结果基本一致。

致使评判等级有出入的原因在于在本文的等级区间划分并不是均匀划分，而是采用黄金分割法作为分点依据，倘若使用均匀划分，那么评判结果将会完全一致。这点在基于云模型的综合评判法的云相似度可以看出，“中等”等级的相似度为0.999 9，“较好”等级的相似度为0.999 6，相差0.000 3。两者十分的靠近。事实上，如图7，可直观看出，评价结果十分靠近等级“较好”。

表6 模糊综合评价法评价结果

综上所述，两种方法(传统云模型与模糊综合评判法)的计算所得的惠州市水资源管理等级处于较好水平，且在达标线附近，这与本文的计算结果基本一致，从而说明了本文的计算方法是合理可行的。且通过对比，可知本文的方法更为直观、更为可信与更为稳定。

5 结 论

(1)把云模型应用在水资源管理评价中，能兼顾等级概念的模糊性与随机性，从实际数据分布中抽取等级概念，实现不同层次上的分析与综合。其不仅给出了评价结果的期望值，而且还给出了评价结果的可信度与稳定度，比一般的评价方法给出的信息更为丰富。在权重选择方面采用了熵权法，减少了人为主观因素的影响，使权重更为客观，尽可能地降低了人为打分的模糊性。因此基于云模型和熵权法的模糊综合评价模型为水资源管理评估提供给了一种新的思路。

(2)在对惠州市的实例分析中，可以看出最终的评价等级与次级指标的评估等级表现有所差异，可直观清晰地从图表数据中了解各指标所处位置与等级隶属程度，其中在用水效率上已经达到较好的水平；而水资源开发利用与水功能区限制纳污这两个指标反映出其管理水平处于中等达标状态，然而仍然有待加强；综合指标最终的水资源管理等级定义为中等，然而却已经较为接近较好程度，管理者可根据各指标反映的问题做出实际调整，以期最终达到三条红线所规定的目标。

□

[1] 左其亭,张保祥,王宗志,等. 2011年中央一号文件对水科学研究的启示与讨论[J]. 南水北调与水利科技,2011,(5):68-73.

[2] 左其亭,胡德胜,窦 明,等. 基于人水和谐理念的最严格水资源管理制度研究框架及核心体系[J]. 资源科学,2014,(5):906-912.

[3] 黄曼丽,朱 凌,尹 华,等. 基于熵权的多目标综合评价方法在水利工程中的应用[J]. 中国农村水利水电,2008,(12):99-102.

[4] 柳 军. 模糊综合评价在水环境质量评价中的应用研究[D]. 重庆：重庆大学,2003.

[5] 罗军刚,解建仓,阮本清. 基于熵权的水资源短缺风险模糊综合评价模型及应用[J]. 水利学报,2008,(9):1 092-1 097,1104.

[6] 周晓蔚,王丽萍,张验科. 基于最大熵的河流水质恢复能力模糊评价模型[J]. 中国农村水利水电,2008,(1):23-25.

[7] 石 佳,纪昌明,张验科,等. 基于RVA的建库后下游河流生态风险评价研究[J]. 中国农村水利水电,2013,(8):7-11.

[8] 邸凯昌,李德毅,李德仁. 云理论及其在空间数据发掘和知识发现中的应用[J]. 中国图象图形学报,1999,(11):32-37.

[9] 李德毅,杜 鹢.不确定性人工智能[M].北京：国防工业出版社,2005.

[10] 张秋文,章永志,钟 鸣. 基于云模型的水库诱发地震风险多级模糊综合评价[J]. 水利学报,2014,(1):87-95.

[11] 魏光辉,马 亮. 基于正态云模型的区域水资源承载力评价[J]. 节水灌溉,2015,(1):68-71.

[12] 张仕斌,许春香. 基于云模型的信任评估方法研究[J]. 计算机学报,2013,(2):422-431.

[13] 张仕斌,许春香,安宇俊. 基于云模型的风险评估方法研究[J]. 电子科技大学学报,2013,(1):92-97,104.

[14] 李克飞,纪昌明,张验科. 水电站水库群多目标联合调度风险评价决策研究[J]. 中国农村水利水电,2012,(10):120-122.

[15] 李继伟,纪昌明,张新明,等. 基于改进TOPSIS的水库水沙联合调度方案评价[J]. 中国农村水利水电,2013,(10):42-45.

[16] 张晓星,纪昌明,彭 杨,等. 基于最大熵法的河道行洪风险评估[J]. 中国农村水利水电,2009,(12):70-73.

[17] 何 洋,纪昌明,田开华,等. 基于最大熵原理的径流预报误差分布规律研究[J]. 中国农村水利水电,2016,(11):115-120.

[18] 刘 霞,王丽萍,天谷孝夫. 达拉特旗井灌条件下农田水利用及地下水动态分析研究[J]. 中国农村水利水电,2011,(10):29-32.

[19] 赵璧奎,王丽萍,张验科,等. 大型城市原水系统水质变化过程评价方法研究[J]. 中国农村水利水电,2012,(12):84-87.

[20] 李 琪,徐裕生,张志杰. 黄金分割法在水处理实验中的应用[J]. 中国农村水利水电,1999,(12):12-13.