基于数值模拟的新疆灌溉水田间入渗系数研究

刘苗苗，杨 丽，李 斐，王水献

(兰州大学资源环境学院，兰州 730000)

0 引 言

在我国干旱内陆地区，地下水是人类生活、生产以及维护生态环境重要的淡水资源，是灌溉用水的主要来源之一，而地下水补给来源超过80%来自于渠系及田间渗漏[1]。新中国成立后的几十年来，大多数地区主要采用了传统的漫灌、畦灌等方式，这些灌溉方式渗漏量很大。随着规模化节水灌溉技术的发展，地下水补排关系发生了一系列复杂的变化，地下水资源的变化引起了干旱区一系列的生态问题。为精确评价地下水资源量，关键问题是确定合理的灌溉水田间入渗系数，这对地下水资源的可持续发展具有重要意义。

新疆典型的大陆性干旱气候及其地域限制使得农业生产对灌溉具有很强的依赖性，农业用水约占总生产生活用水量的95%且用水来源以地表水为主，地下水为辅[2]，其中地下水的持续开采利用使得地下水位下降，同时，新疆规模化节水灌溉面积发展较快且高于全国平均水平[3]，使得地下水补给量减少，加剧了地下水位的下降，这些都与规模化节水灌溉的发展有关，目前常见的节水灌溉技术具有显著的节水效果，例如滴灌条件下田间没有产生明显的土壤水渗漏现象[4]，采用高频次小定额的灌水方式也能有效避免深层渗漏损失[5]。目前对农田土壤水深层渗漏量的测定主要有水量平衡法、定位通量法、数值模拟法等[6-7]。其中模型模拟法被广泛应用于华北平原、黄淮海豫北平原、河套灌区等[8-10]，同时，计算机模型已经发展成一种分析灌溉、土壤水分入渗[11]和作物生长[12]的重要工具。毕经伟用HYDRUS-1D模型对土壤水渗漏及硝态氮的淋失特征进行了模拟分析[13]，胡克林用该模型对选取不同下边界条件下的土壤水渗漏情况进行模拟[14]，但灌溉用水的变化量是通过平衡方程计算的，通过模型对此进行的模拟研究相对较少。

本研究选取新疆三工河流域试验区为研究对象，利用已有的田间试验观测数据，构建田间一维土壤水分数值模型，并对模型进行率定，利用校正后的数值模型，研究了不同灌溉模式下的灌溉水田间入渗系数，研究结果对干旱区规模化节水措施下地下水资源的定量评价和管理有着重要的参考依据。

1 材料与方法

1.1 研究区概况

三工河流域位于天山北麓中段东部，准噶尔盆地南缘，地理坐标43°09′～45°29′N，87°47′～88°17′E，行政区属新疆昌吉州阜康市。流域总面积1 670 km2，属内陆干旱区，流域内主要有三工河、四工河、水磨河，均发源于博格达山北麓。流域多年平均降水量为207.8 mm，多年平均蒸发量为1 850.7 mm，昼夜温差大，夏季炎热干旱，冬季寒冷多风，水资源短缺，植被稀少，但光热资源丰富，灌溉农业具有很大潜力[15]。

1.2 田间监测试验

在三工河流域的城关乡张家庄村开展灌溉入渗试验，监测土壤含水量的变化情况，利用中子仪测定不同时刻的土壤含水量，监测期为2004年4月24日至8月的灌溉期，监测方法为灌水前1天、灌水结束后地面无积水时(1～3 h)、灌水后第1天、第2天、第3天，其余时段每月5、10、15、20、25日和月末日观测。

根据观测资料拟定模拟土层深度为200 cm并分为5层，0～20 cm是砂壤土，20～50 cm是砂质黏壤土，50～80 cm是粉土，80～120 cm是砂性土，120～200 cm是砂壤土。各土壤水力参数为HYDRUS-1D模型土壤水分特征曲线参数模块的数值，各经验值如表1所示。

表1 试验区土壤水力参数经验值Tab.1 Empirical value of the soil hydraulic parameters in study area

1.3 数值模型

1.3.1 模型简介

HYDRUS-1D是由美国农业部盐土实验室开发的一款用于模拟水分、溶质和能量在一维非饱和多孔隙介质中运移的一维数值模型[16]，模型考虑了作物根系吸水和土壤持水能力的滞后影响[17]，适用于恒定或非恒定的边界条件且具有灵活的输入输出功能。

1.3.2 时间和空间离散

模拟时间从2004年4月25日至7月20日总计87 d，采用变时间步长剖分方式，根据收敛迭代次数调整时间步长，允许最小时间步长为0.001 d，最大时间步长为1 d。

模型模拟土层为深度200 cm的垂直剖面，将一维的土壤剖面按2 cm等间隔剖分为101个单元。在上述土层剖分的基础上，根据土壤剖面特性和实测的土壤质地，将土壤分为0～20、20～50、50～80、80～120、120～200 cm五层，并赋予不同的土壤水力参数值，并分别在10、30、40、80、120和200 cm深处设置6个观测点。

1.3.3 蒸散发的计算

根据1998年联合国粮农组织(FAO)推荐的Penman-Monteith(PM)公式作为计算参考作物蒸发蒸腾量的标准方法[18]，所用到的气象数据由中国气象数据网提供：

(1)

式中：ET0为参考作物蒸发蒸腾量，mm/d；Rn为净太阳辐射，J/(m2·d)；G为土壤热通量，J/(m2·d)；ea为饱和水汽压，kPa；ed为实际水汽压，kPa；γ为湿度计常数，kPa/℃；Δ为温度-饱和水汽压关系曲线在T处的切线斜率，kPa/℃；U10为距地表10 m处的风速，m/s。

HYDRUS模型应用Beer定律，将Penman-Monteith公式计算得到的潜在蒸散量分为潜在蒸发(Ep)和潜在蒸腾(Tp)：

(2)

式中：k为冠层的消光系数，模型中默认为0.39[17]；LAI为叶面积指数，参考值基于LAI预测函数模型[19]，播种前取值0.3，幼苗期1.5，开花期2.3，结荚期为3。

1.4 土壤水力参数敏感性分析

用HYDRUS-1D模型模拟田间土壤水分运动的精度主要取决于土壤水力参数的选取，为提高模型精度，需要对参数进行适当调整，首先采用单因素敏感性分析法进行参数敏感性分析[20]，即每次只选择某一土层的某一参数，在模型能正常运行的情况下对参数进行适当改变，得到新的模拟结果，利用模拟前后的田间含水量平均值的变化量进行敏感性系数S的计算，定量分析某一参数的改变对模型结果的影响程度。

(3)

式中：X是参数值；Y是模拟值；ΔX和ΔY是两者的改变量。

1.5 误差分析

采用均方根误差(root mean square error，RMSE)和相对误差(relative error，RE)两个评价指标来定量评价参数改进前后模型的土壤含水量模拟效果[21]，各评价指标的计算公式为：

(5)

式中：si和oi分别为第i个样本的模拟值和实测值；N为样本个数。

均方根误差(RMSE)反映模拟值与实测值绝对误差的平均程度，相对误差(RE)反映模拟值与实测值总量之间的相对误差。

2 结果与讨论

2.1 参数敏感性分析和模型的率定

根据公式(3)分析得到的不同深度土壤含水量对应的敏感性系数如表2所示，各层土壤的水力参数对相应土层的土壤含水量影响最大，对于0～20、20～40、80～120和120～200 cm土层，敏感性系数超过0.4的参数有土壤饱和含水率θs、孔径指数n；对于40～80 cm土层，敏感性系数超过0.4的参数只有孔径指数n；土壤含水率对其他参数的变化敏感程度不高且随着土层深度的增加敏感性降低；各土层的土壤含水量对土壤残余含水率θr及a都不敏感，但对孔径指数n均敏感，这是因为van Genuchten 模型中n为ab的指数次幂，所以对土壤含水量均有影响。

表2 各层土壤水力参数敏感性分析Tab.2 Soil hydraulic parameters sensitivity analysis in each layer

注：表中数值均为敏感性系数的绝对值，*表示敏感性系数绝对值超过0.2。

在模型中输入试验田的特征参数、降雨、计算蒸散发所用数据和初始土壤含水量分布。先按土壤水力参数经验值进行模拟，在一个完整灌溉周期内，选取4月25日至5月31日的土壤含水量实测值与模拟值进行对比，再通过敏感性分析得到的结果重点对相关参数进行适当调整，重复调参直至实测值与模拟值充分接近，达到两者之间均方根误差最小，所得参数即为最终率定参数，模型识别后的参数见表3。

表3 模型识别后的土壤水力参数值Tab.3 Model verification of the soil hydraulic parameter values

将率定后的土壤水力参数重新代入模型对土壤含水量进行模拟，采用6月1日至7月20日的土壤含水量实测值对模型进行验证，验证结果的散点图如图1所示，各评价指标的值如表4所示。

图1 试验区土壤含水量模拟值与实测值对比图Fig.1 Comparison of simulation values with observation values of soil water contents in study area

图1是土壤含水量模拟结果的散点图，表层土壤含水量的模拟结果相对较差，深层土壤含水量的模拟结果相对较好，各点均匀分布在1:1线两侧。

表4 土壤含水量模拟值与实测值误差分析Tab.4 The result of error analysis between the simulation value and the observation value

从表4可以看出，模型在模拟40、80、120、200 cm深度土壤含水量时效果良好，但在模拟土壤浅层10、20 cm含水量时与实测值存在一定偏差，分析原因主要是由于灌溉后土壤水未完全下渗时土壤含水量偏大造成的。总体来看模拟结果良好，运用HYDRUS-1D模型对该条件下土壤水分运移进行模拟是可行的。

2.2 不同灌溉模式下的田间入渗系数

利用识别后的模型，参考2014年新疆维吾尔自治区关于三工河流域的农业灌溉用水定额地方标准，选取豆类作物为研究对象，分别对传统灌溉(4 500 m3/hm2)和节水灌溉(3 375 m3/hm2)下的田间土壤水运移进行模拟，分析水量平衡结果，确定合理的田间灌水定额。初始灌溉方式及灌水定额详见表5，将豆类的生长期(87 d)分为播前，幼苗期，开花期和结荚期4个阶段，再根据作物不同生长阶段的需水量确定灌水定额及次数。

2.2.1 传统灌溉水量平衡分析

根据表5所示的灌溉模式模拟的水量平衡结果如表6所示，不同生长阶段的耗水量不同，生长初期，作物耗水以蒸散发为主，随着作物的生长，根系吸水量逐渐增大，模型输出的蓄变量反映模拟土层与其下土层的水量交换。模拟蓄变量为157.32 mm，水量平衡计算值为156.58 mm，误差0.5%。降水和灌溉总量的48.8%为渗漏损失，同时，渗漏量占灌溉量的54.2%。

表5 不同灌溉方式及灌水定额Tab.5 Irrigation scheduling and irrigation quota

在同样的土壤质地条件下，任玉忠研究了灌溉水深层渗漏特性及耗水规律，通过HYDRUS-1D模拟及数值计算下的传统灌溉田间入渗系数分别为0.6和 0.551[22]。陈莉研究得出新疆灌溉水田间入渗系数均值为0.486[23]，周和平计算出新疆东部2009年的系数为0.534[24]。孙宝林研究表明新疆灌溉区为地下水补给来源的主要区域，8.4%的平原灌溉区所补给的地下水量占总补给量的82.6%[25]。综上所述，灌溉水的田间入渗系数介于0.5～0.7之间，为地下水提供大量补给，随着节水灌溉技术的推广，需对系数做进一步的研究。

表6 传统灌溉模式下的水量平衡Tab.6 Water balance of conventional irrigation

2.2.2 节水灌溉水量平衡分析

根据表6作物各生长阶段的需水量及蒸散发[26]，其中作物需水量为参考作物蒸散发乘作物系数[27]，由式(1)可得新疆三工河流域的参考作物蒸散发为622.3 mm。对表5所示的节水灌溉模式进行模拟的结果如表7所示，模型模拟蓄变量为154.90 mm，计算值为153.06 mm，误差1.2%，与表6相比，新的灌溉模式下作物各生长阶段的渗漏损失均有所降低，降水和灌溉总量的29.4%为渗漏损失，同时，渗漏量占灌溉量的33.7%，总体来看，灌溉水渗漏损失由54.2%降到33.7%。

节水灌溉模式下灌溉水田间入渗系数有所降低，究其原因，是在满足作物各阶段需水量的同时，降低了灌水定额，增加了灌水次数，使得作物不同生长期的入渗系数均有所降低；本研究中作物播前期及幼苗期的入渗系数略大于总的入渗系数，因此还可以对该生长期灌溉水量进行调整，在之后的生产中，可以针对不同作物各生长阶段的不同需水量来调整灌水定额及次数，并结合当地的气候条件，制定适合不同作物的节水灌溉模式。

表7 节水灌溉模式下的水量平衡Tab.7 Water balance of water-saving irrigation

总结近年来各学者基于不同评价方法对新疆各地区灌溉水渗漏问题的研究，与本文模型计算结果进行对比。如表8所示，基于不同方法得到的传统灌溉模式下新疆灌溉水田间入渗系数为0.6左右，节水灌溉模式下的田间入渗系数为0.3左右，变幅较大为节水灌溉模式不同所致。本文模拟的两种灌溉模式下的系数分别为0.542和0.337，与前人的研究成果相近，具有较高的可靠性。

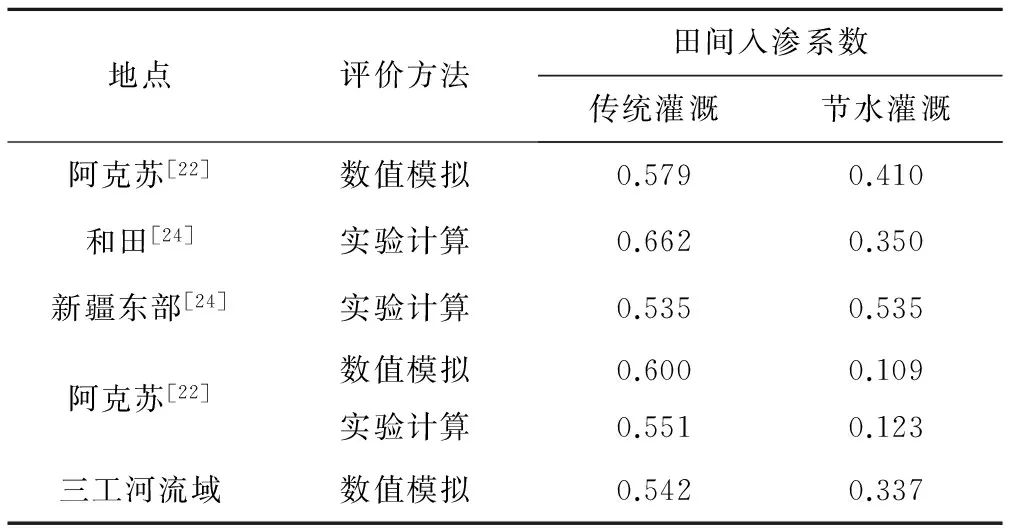
表8 新疆各地区田间入渗系数结果对比Tab.8 Comparison of field infiltration coefficient in Xinjiang

3 结 语

应用HYDRUS-1D模型模拟了豆类作物在整个生长期的土壤水分动态变化，并对田间土壤水量平衡进行分析计算，误差控制在1.5%以内，表明利用该模型对流域进行灌溉水田间入渗系数预测是可行的。

通过土壤水分动态变化分析及田间土壤水量平衡计算，在传统灌溉模式下，作物四个生长期的田间入渗系数分别为0.602，0.563，0.525，0.462；在同样的条件下，考虑作物在不同生长期的需水量，所得节水灌溉的系数分别为0.392，0.419，0.325，0.286，不同生长期入渗系数的不同会导致地下水资源周期性变化，对新疆地下水的开发利用具有参考价值。

传统灌溉下的田间入渗系数介于0.542～0.662之间，与此同时，节水灌溉的田间入渗系数介于0.337～0.410之间。规模化节水灌溉技术的推广使渗漏损失减少了近20%，有效的提高了水资源利用效率，然而这加剧了地下水资源的衰减。对干旱地区来讲，田间入渗系数的降低意味着地下水的补给量减少，在现有的开采模式下必然会加剧地下水位的持续下降。随着限制开采等措施的实施，地下水资源也随之发生变化，将所得的灌溉水田间入渗系数与新疆各灌区结合，能为新疆地下水资源的评价与管理提供理论支持。

□

[1] 罗格平, 周成虎, 陈 曦. 从景观格局分析人为驱动的绿洲时空变化——以天山北坡三工河流域绿洲为例[J]. 生态学报, 2005,25(9):2 197-2 205.

[2] 张 龙, 张 娜. 新疆农业节水现状及对策研究[J]. 中国农村水利水电, 2010,45(7):43-45.

[3] 周和平, 王 忠, 徐小波. 新疆高效节水灌溉发展规模研究[J]. 中国农村水利水电, 2010,45(12):18-21.

[4] 孙泽强, 康跃虎, 刘海军. 喷灌冬小麦农田土壤水分分布特征及水量平衡[J]. 干旱地区农业研究, 2006,24(1):100-107.

[5] 岳 兵. 渗灌技术存在问题与建议[J]. 灌溉排水, 1997,16(2):40-44.

[6] 于红梅. 控制土壤含水量对蔬菜产量及露地菜田水分渗漏量的影响[J]. 中国农学通报, 2007,23(4):232-236.

[7] 冀荣华, 王婷婷, 祁力钧, 等. 基于 HYDRUS-2D 的负压灌溉土壤水分入渗数值模拟[J]. 农业机械学报, 2015,46(4):113-119.

[8] 龚元石, 李保国. 应用农田水量平衡模型估算土壤水渗漏量[J]. 水科学进展, 1995,6(1):16-21.

[9] 朱安宁, 张佳宝. 黄潮土的土壤水渗漏及硝态氮淋溶研究[J]. 农村生态环境, 2003,19(1):27-30.

[10] 郝芳华, 欧阳威, 岳 勇, 等. 内蒙古农业灌区水循环特征及对土壤水运移影响的分析[J]. 环境科学学报, 2008,28(5):825-831.

[11] Skaggs T H, van Genuchten M T, Shouse P J, et al. Macroscopic approaches to root water uptake as a function of water and salinity stress[J]. agricultural water management, 2006,86(1):140-149.

[12] Tafteh A, Sepaskhah A R. Application of HYDRUS-1D model for simulating water and nitrate leaching from continuous and alternate furrow irrigated rapeseed and maize fields[J]. Agricultural Water Management, 2012,113(10):19-29.

[13] 毕经伟, 张佳宝, 陈效民, 等. 应用 HYDRUS-1D 模型模拟农田土壤水渗漏及硝态氮淋失特征[J]. 农村生态环境, 2004,20(2):28-32.

[14] 胡克林, 肖新华, 李保国. 不同类型下边界条件对模拟灌溉农田水分渗漏的影响[J]. 水科学进展, 2006,17(5):665-670.

[15] 占车生, 丰华丽, 马灵玲, 等. 新疆三工河流域农业需水量预测与分析[J]. 干旱区地理, 2009,32(3):438-444.

[16] Simunek J, Van Genuchten M T, Sejna M. The HYDRUS-1D software package for simulating the one-dimensional movement of water, heat, and multiple solutes in variably-saturated media[J]. University of California-Riverside Research Reports, 2005,112(3):1-240.

[17] Van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil science society of America journal, 1980,44(5):892-898.

[18] Allen R G, Pereira L S, Raes D, et al. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56[J]. FAO, Rome, 1998,300(9):D05-109.

[19] 吴立峰, 张富仓, 王海东, 等. 新疆棉花亏缺灌溉叶面积指数模拟研究[J]. 农业机械学报, 2015,46(1):249-258.

[20] 高 跃. 基于 HYDRUS 模型的红壤坡耕地水分动态研究[D]. 武汉：华中农业大学, 2013.

[21] 马 欢, 杨大文, 雷慧闽, 等. Hydrus-1D 模型在田间水循环规律分析中的应用及改进[J]. 农业工程学报, 2011,27(3):6-12.

[22] 任玉忠. 干旱区枣园土壤水深层渗漏数值模拟研究[D]. 乌鲁木齐：新疆农业大学, 2010.

[23] 陈 莉, 吴旭春, 陈 敏. 新疆农业灌溉用水节水潜力分析[J]. 新疆农业大学学报, 2004,27(S1):116-118.

[24] 周和平, 张明义, 周 琪, 等. 新疆地区农业灌溉水利用系数分析[J]. 农业工程学报, 2013,29(22):100-107.

[25] 孙宝林, 魏 琳, 杨 瑾. 新疆地下水资源量及开采潜力分析[J]. 内蒙古水利, 2005,102(2):10-12.

[26] 史晓楠, 王全九, 王 新, 等. 参考作物腾发量计算方法在新疆地区的适用性研究[J]. 农业工程学报, 2006,22(6):19-23.

[27] 闫浩芳. 内蒙古河套灌区不同作物腾发量及作物系数的研究[D]. 呼和浩特：内蒙古农业大学, 2008.