基于LR模糊数的水电机组竖向振动传递路径分析

职保平,秦净净,许新勇,张宏战

(1.小流域水利河南省高校工程技术研究中心,河南开封475004；2.黄河水利职业技术学院,河南开封475004；3.华北水利水电大学,河南郑州450000；4.大连理工大学建设工程学部,辽宁大连116023)

完整的振动系统由振源、传导路径和受振体3部分组成,水电机组振动系统的动力分析主要集中于水力[1-2]、机械[3- 4]、电磁[5],及其耦合振源[6]的模拟与表达,以及厂房、机组振动响应的研究[7],而振动传导路径作为振动系统的主要组成,目前的研究仅处于探索阶段[8],其中,复杂系统所受的耦合振动源可通过不同的路径传递到多个位置,如何建立振动的传递系统模型并预测各种路径传递率具有十分重要的现实意义。

在水电机组中,由于各种不确定因素的影响,其物理参数和几何尺寸同样会呈现出不确定性,从而使刚度矩阵、质量矩阵存在不确定性,并最终导致结构的特征值是不确定的,这样的不确定性往往以随机变量、模糊变量、区间变量等数学形式来表现,其中随机变量需大量样本及概率分布,模糊变量在特定条件具有十分显著的优势。吕恩琳[9]引入α水平截集处理,得到随机区间平衡方程；郭书祥[10]等根据模糊的区间形式表达和运算性质给出模糊数的运算规则,从而导出有限元静力控制方程的求解方法；雷震宇[11]等根据信息熵的理论将模糊有限元方程转化为一个等效的具有相同区间上均匀分布随机变量的随机有限元方程。

本文在前期工作的基础上,建立伞式混流式水轮发电机组振动分析模型,引入质量、阻尼、刚度等传递路径参数的模糊性,根据模糊数的区间形式表达与区间运算的性质,提出基于LR模糊数的水电机组振动传递路径系统中传递率的度量方法,并给出传导路径的排序,为振动传递路径系统的分析提供理论依据。

1 LR模糊数及其运算

根据Zadeh[12]的模糊集合理论,L-R型模糊数的隶属函数为

(1)

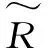
(2)

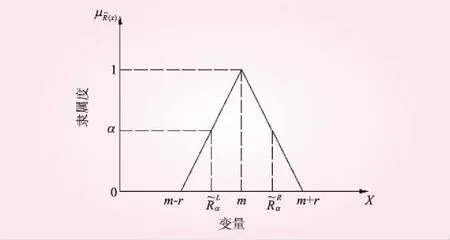
图1 LR三角型模糊数

2 LR模糊变量的运算规则

(3)

其中,

(4)

3 水电机组振动传导路径模糊性分析

现场和模型试验表明,水轮机振动向厂房结构传递的路径一般有下述三种途径[1]：①转轮—轴系—轴承—固定部件(机架、顶盖)—厂房,由转轮部分通过轴系传递至机墩部件,其方向为轴向振动；②充水水压—蜗壳—厂房,通过蜗壳内部水体直接通过蜗壳传递至周围混凝土,其方向可分解成轴向振动和径向振动；③转轮—转轮负压区—顶盖—厂房,通过转轮传递至顶盖,通过环板传递至蜗壳及外围混凝土,其方向为轴向。目前水力振源诱发的竖向振动研究主要集中在路径①,并忽略路径②、③的作用[2]。

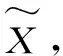
(5)

(6)

根据模糊数运算法则得

(7)

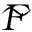
(8)

本文用路径传递率对振动传递系统的路径重要性进行评价,传递率为传递力的力幅与激励力幅之比,即

(9)

4 算例分析

某巨型水电站伞式机组振动传递路径如图2,不考虑蜗壳及其下部结构影响,假设激励为单频简谐激励,区间参数均值如下：质量m1=8.28×104kg,m2=1.042×106kg,m3=3.29×105kg,m4=9×105kg,m5=1.2×105kg,m6=1.39×105kg,m7=8.92×105kg,m8=1.15×105kg；刚度k1=7.26×1010N/m,k3=5.72×1010N/m,k4=2.32×1010N/m,k51=2.20×1012N/m,k52=9.41×109N/m,k6=7.70×109N/m,k7=4.26×108N/m,k81=1.73×108N/m,k82=1.73×1010N/m；阻尼c1=5.48×106N·s/m,c3=4.11×106N·s/m,c4=1.02×107N·s/m,c51=2.56×107N·s/m,c52=7.51×104N·s/m,c6=1.64×106N·s/m,c7=9.74×105N·s/m,c81=2.23×105N·s/m,c82=9.99×104N·s/m。

图2 伞式机组竖向振动简化模型

这些参数中,油膜、水封的刚度参数由于非线性明显、难以测量等因素导致具有很强的模糊性,因此取k51,k81,c51,c81的模糊边界范围为均值的0.1,k82,c82的模糊边界范围为均值的0.1,机墩等质量单元模糊边界范围为半径的0.01。用文中的方法求得α水平截集在0.5～1变化范围内轴系统以及顶盖系统随激励频率变化的传递率曲线(见图3)以及不同截集下轴系统和顶盖系统传递率在固有频率处的变化曲线(见图4)。

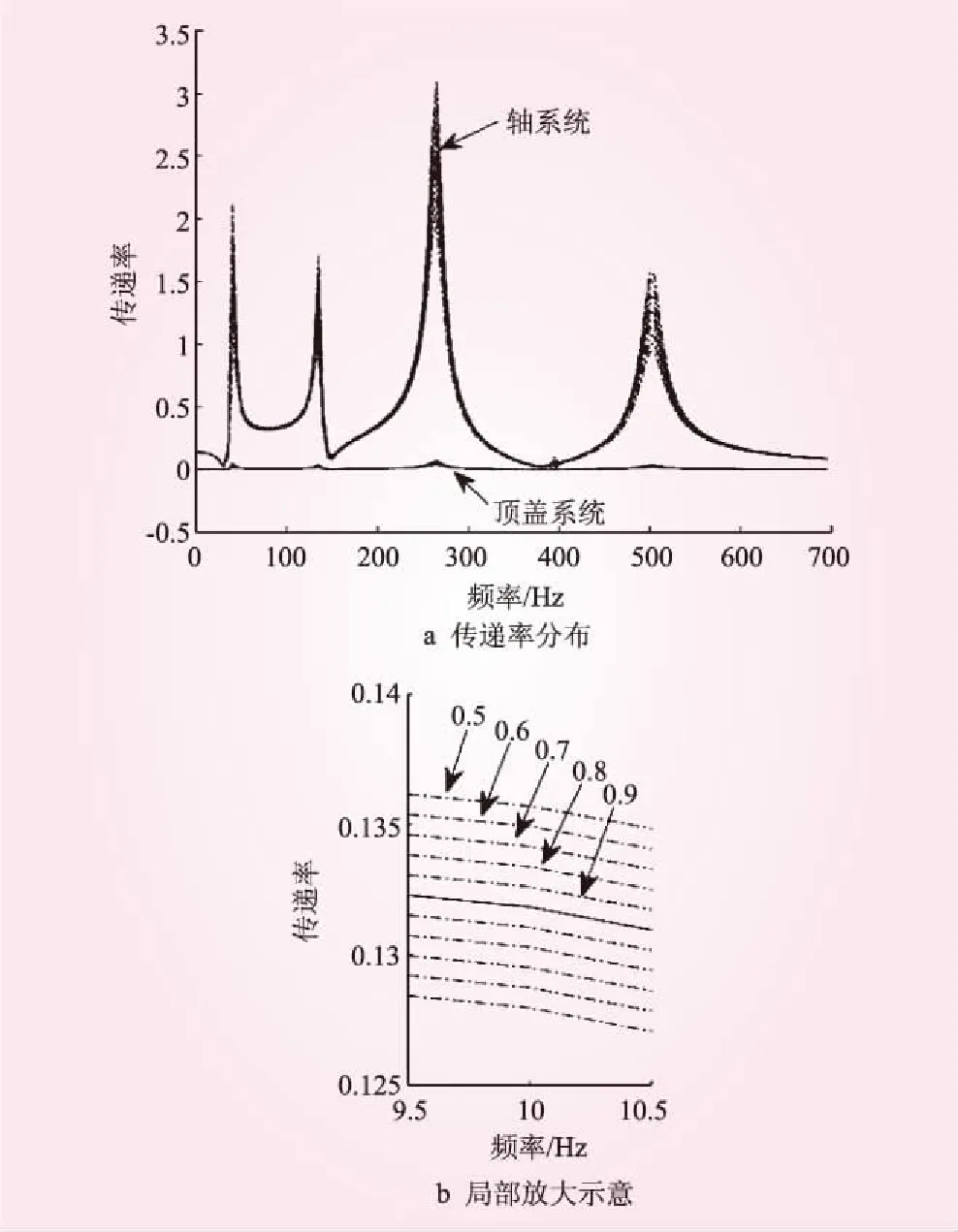
图3 各路径在不同截集下的传递率分布及局部放大示意

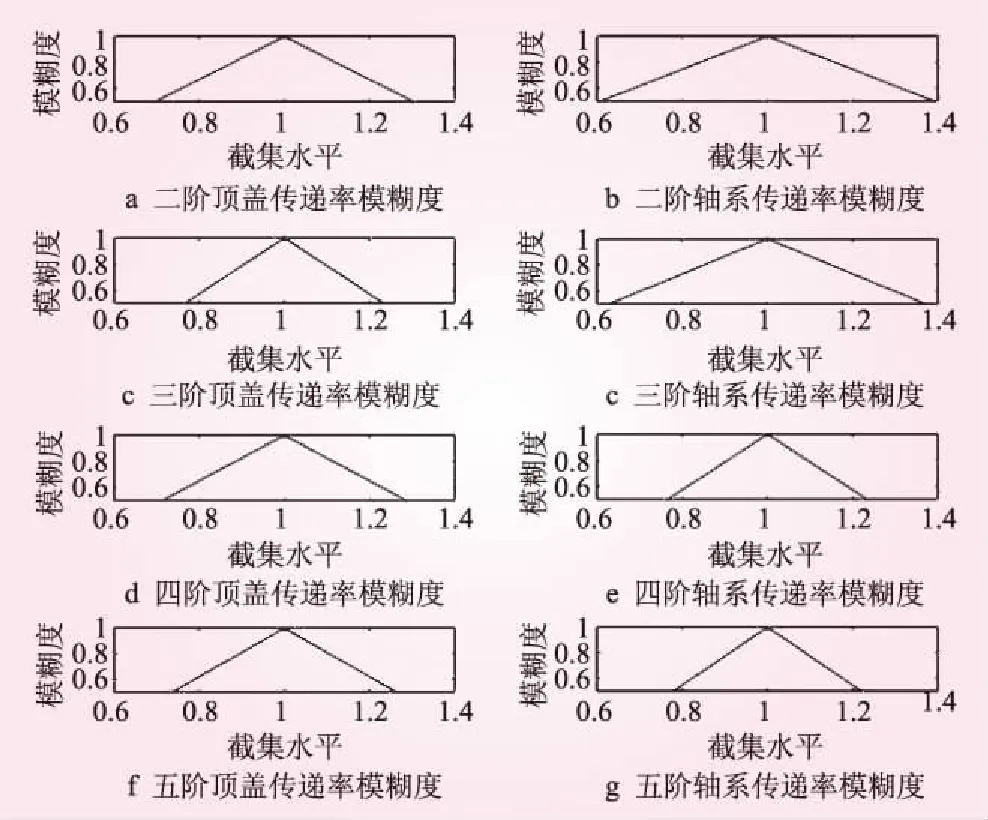
图4 各截集下不同固有频率处的路径传递率模糊度

图3表明：①不同截集水平下,当激振力频率在系统频率处,两条路径传递率均产生峰值；②轴系统的传递率明显高于顶盖系统,表明轴系统是振动传导的主路径。图4为第二阶至第五阶固有频率处,在不同截集下的路径传递率模糊度,纵坐标是α的取值范围,横坐标是与传递率均值相比较的边界范围,图4表明：①当刚度阻尼为三角型模糊函数时,顶盖和轴系统的传递率仍然为三角型模糊隶属函数；②各阶固有频率的模糊度并不完全一致,这是由于结构本身的特性所造成的；③结构经过多个模糊结构时,传递率的模糊范围仍然控制较好,最大边界范围仅为73.8%～126%的均值。

5 结 论

由于问题的复杂性,得到的数据信息常存在一定的模糊性,本文基于区间运算和振动理论,利用模糊变量的区间运算形式与性质,根据输入模糊数的α水平截集,给出水电机组轴系统和顶盖系统传递率的模糊数分布,为进一步评估基于模糊因子的各路径贡献度奠定基础。算例分析表明考虑刚度阻尼变量的模糊性时,在不同的截集水平下,轴系统和顶盖系统的传递率均在系统频率处达到最大值,轴系统大于顶盖系统,且传递率的模糊范围控制也较好。

[1] 黄剑峰, 张立翔, 王文全, 等. 混流式水轮机三维非定常流分离涡模型的精细模拟[J]. 中国电机工程学报, 2011, 31(26): 83- 89．

[2] XIAO Y X, WANG Z W, ZHANG J, et al. Numerical predictions of pressure pulses in a Francis pump turbine with misaligned guide vanes[J]. Journal of Hydrodynamics, 2014, 26(2): 250- 256．

[3] 王海军, 练继建, 杨敏, 等. 混流式水轮机轴向动荷载识别[J]. 振动与冲击, 2007, 26(4): 123- 125．

[4] 孔达, 李忠刚, 焦映厚, 等. 水轮机转子-密封系统模型及其非线性动力学特性分析[J]. 水力发电学报, 2013, 44(4): 462- 469．

[5] 宋志强, 刘云贺. 考虑电磁刚度的水电机组转子轴承系统弯扭耦合振动研究[J]. 水力发电学报, 2014, 33(6): 224- 231．

[6] 李兆军, 蔡敢为, 杨旭娟, 等. 混流式水轮发电机组主轴系统非线性全局耦合动力模型[J]. 机械强度, 2008, 30(2): 175- 183．

[7] 徐伟, 马震岳, 职保平. 基于功率流理论的大型水电站厂房结构脉动压力频响分析[J]. 水利学报, 2012(5): 615- 622．

[8] SINGH R, KIM S. Examination of multi-dimensional vibration isolation measures and their correlation to sound radiation over a broad frequency range[J]. Journal of Sound and Vibration, 2003, 262(3): 419- 455．

[9] 郑宏民, 薛晶, 李玉忍. 温度场模糊随机有限元法研究[J]. 计算机仿真, 2012, 29(3): 167- 171．

[10] 郭书祥, 吕震宙, 冯立富. 模糊运算和模糊有限元静力控制方程的求解[J]. 应用数学和力学, 2002(9)： 936- 942．

[11] 雷震宇, 陈虬. 基于信息熵的模糊随机结构有限元法[J]. 力学季刊, 2001, 22(3): 340- 345．

[12] ZADEH L A. Fuzzy sets as basic for a theory of possibility[J]. Fuzzy Sets and Systems, 1978, 1(1): 3- 28．

[13] 万中, 梁文冬, 卢宗娟. 模糊数的隶属度区间分布函数[J]. 重庆理工大学学报: 自然科学版, 2011, 25(1): 107- 112．

[14] 于少伟. 基于区间数的模糊隶属函数构建[J]. 山东大学学报: 工学版, 2010(6): 32- 35, 93．