乌江梯级水电站短期优化调度研究

曹 辉

(1.中国长江三峡集团公司,北京100038;2.三峡水利枢纽梯级调度通信中心,四川成都610041)

随着厂网分开、电力市场改革的不断深入,水电站作为电力市场主体之一,其角色和经营目标发生了明显变化。如何调度梯级水电站,达到降低成本、优化运行的目的,是每个电力企业迫切需要解决的问题。水电站短期优化调度是提高发电收益的重要手段[1-2]。短期优化调度能在考虑电站水情、电力市场环境及电站特点等因素的情况下,制定优化的竞价电量,为参与市场竞价提供重要的决策支持[1]。本文通过选择梯级发电量最大模型对流域不同频率来水情况下梯级电站的发电量进行计算分析,进而总结了乌江梯级电站短期优化调度的发电规律,为梯级电站短期调度计划的制定提供决策指导[3- 6]。

1 流域概况

乌江是长江上游南岸最大的一条支流,全长1 037 km,流域面积8.8 km2,多年平均水量534亿m3。乌江流域为降水补给河流,降雨集中在5～10月,暴雨集中在6、7两个月,洪水主要由暴雨形成。由于暴雨急骤,汇流迅速,洪水涨落快,峰形尖瘦,洪量集中。乌江流域天然落差大,落差达到2 124 m,水量充沛,水力资源丰富,是西部大开发“西电东送”的主要电源点之一。目前,乌江干流已建和将建成的水库群包括洪家渡、东风、索风营、乌江渡、构皮滩、思林和沙沱水库。梯级各水库的特征参数见表1。

2 乌江梯级水库群优化调度模型

2.1 目标函数

为了挖掘乌江梯级水库群优化调度规律,本文建立梯级发电量最大模型,目标函数见式(1),该模型在未来一个调度期水库始、末水位及短期预报入库径流已知的情况下,考虑各水库电站实际情况及电网综合约束,寻求梯级各电站的某种短期联合运行方式,使调度期内梯级电站的总发电量最大[7-9]。

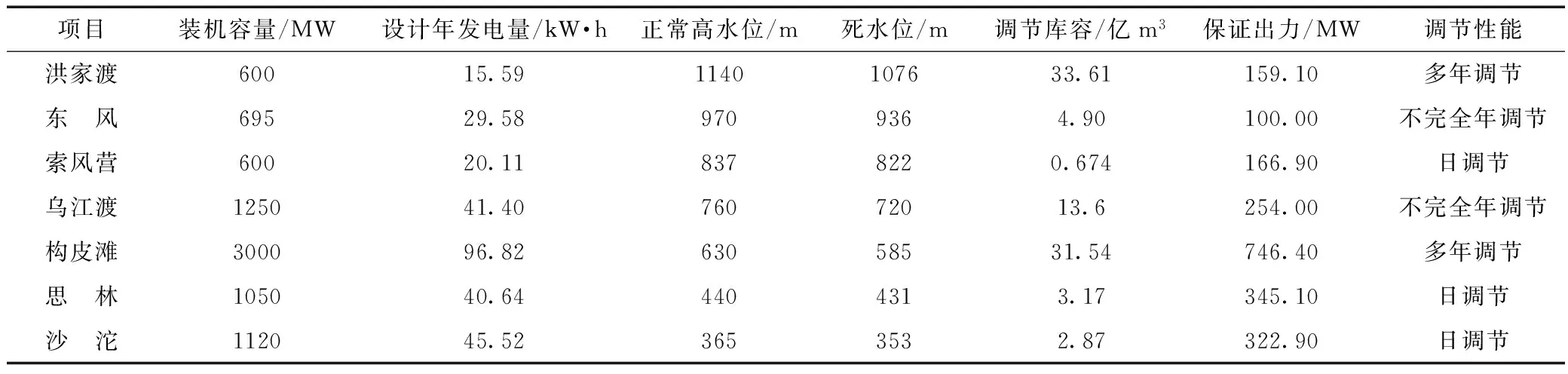
表1 乌江梯级水库群主要特征参数

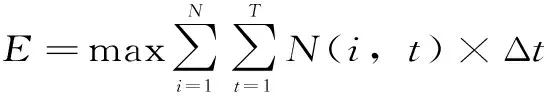
(1)

式中,E为调度期内梯级总发电量；N(i,t)为第i梯级水库t时段平均出力；Δt为时段长；N为梯级水电站数目；T为时段数目。

2.2 约束条件

水量平衡约束

V(m,t+1)=V(m,t)+(QI(m,t)-QO(m,t))×Δt

(2)

蓄水位限制

Zmin(m,t)≤Z(m,t)≤Zmax(m,t)

(3)

出库流量约束

QOmin(m,t)≤QO(m,t)≤QOmax(m,t)

(4)

电站出力限制

Nmin(m,t)≤N(m,t)≤Nmax(m,t)

(5)

式中,QI(m,t)、QO(m,t)为第m级电站、第t时段入库、出库流量；V(m,t)、V(m,t+1)为第m级电站第t时段初、末库容；Zmax(m,t)、Zmin(m,t)为第m级电站第t时段水位变化上、下限；QOmax(m,t)、QOmin(m,t)为第m级电站第t时段出库流量约束上、下限值；Nmax(m,t)、Nmin(m,t)为第m级电站第t时段出力约束上、下限。

2.3 模型求解

本文研究采用关联平衡协调和关联预估协调所组成的混合法对原问题进行分解,选取的协调变量为拉格朗日乘子λit和水库入库流量Qrit,研究中将乌江梯级水电站群分解为7个独立的子系统,即洪家渡水库、东风水库、索风营水库、乌江渡水库、构皮滩水库、思林水库和沙陀水库七个子系统。单库优化采用POA算法进行求解(配合0.618法两阶段寻优),然后通过二级协调器把各子系统连接在一起,并协调各子系统的最优以达到大系统的整体最优,使之满足协调约束,一旦满足则各子系统的最优解即为整个系统最优解。在求解短期优化调度时需要根据具体情况考虑水流时滞问题,因此构造原问题的拉格朗日函数表示为

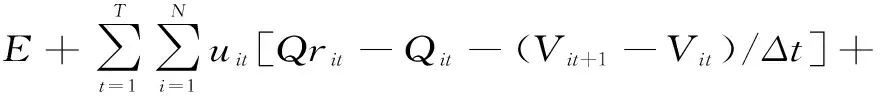
(6)

式中,uit、λit为拉格朗日乘子。由于不考虑梯级系统出力限制要求,构造函数时不需要考虑相应的库恩-塔克乘子,只需进行两级递接控制。

当选取λit和Qrit作为协调变量时,在协调级给定的情况下,对上述拉格朗日函数分解,则可表达成如下加性可分形式:

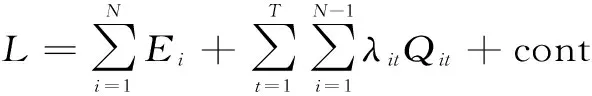
(7)

式中,cont为常数。

由此可将本次研究的大系统问题分解为如下n个子问题

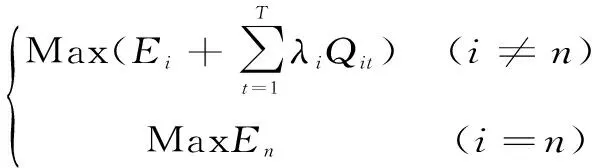
(8)

分别对协调变量Qrit和λit求导可以得出考虑水流时滞的第二级协调器的计算公式为

(9)

(10)

式中,k为迭代次数；ηj为第j水库的出力系数；Hjjt为第j水库t时段的平均水头。

3 梯级水电站发电量最大模型结果及分析

3.1 常规调度

选取不同频率的来水(P=10%、25%、50%、75%、90%),调度期各库的始末水位相同,分别取洪家渡始末水位1 120 m；东风始末水位960 m；索风营始末水位830 m；乌江渡始末水位740 m；构皮滩始末水位630 m；思林始末水位435 m；沙沱始末水位360 m。以梯级发电量最大为目标,采用等流量调节方法,计算乌江干流7库96点日调度,结果如表2、3所示。以上常规调度结果可以看出：

表2 不同频率来水的常规调度计算结果

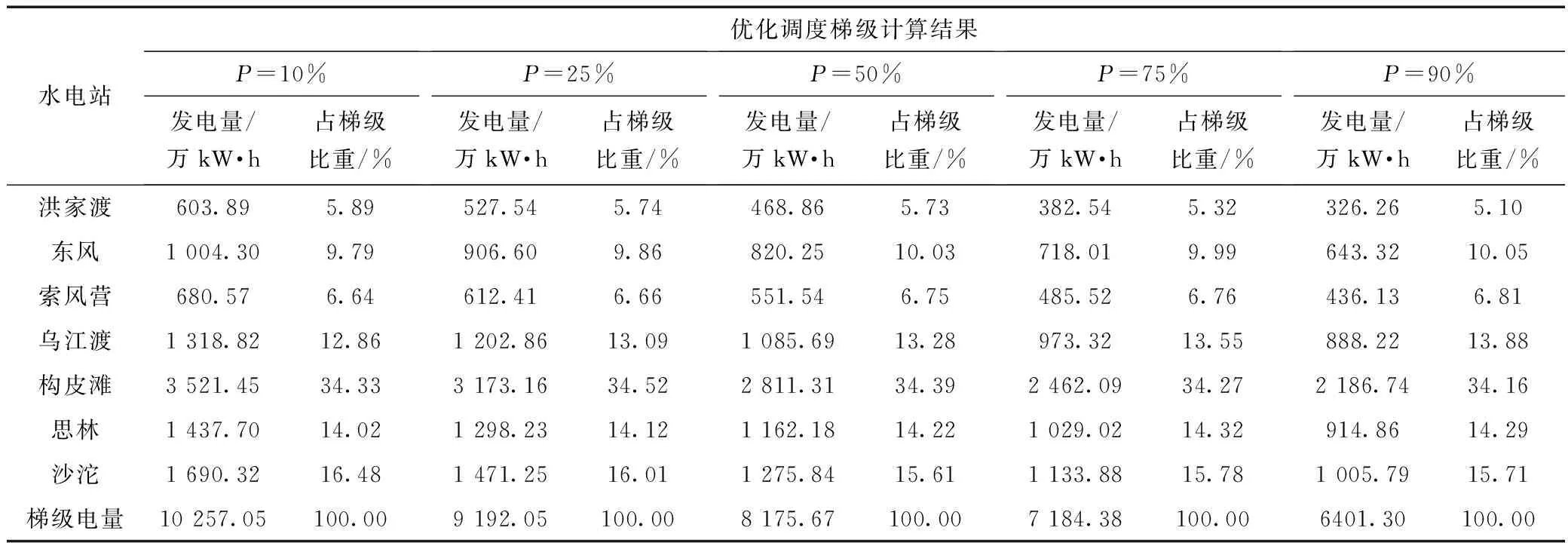
表3 不同频率来水的优化调度梯级计算结果

(1)各库发电量占梯级发电比重不同,随来水改变呈现不同变化趋势。构皮滩占梯级发电比重最大,各频率来水条件下均超过33.61%；而洪家渡最小,仅占5%左右。

(2)随着来水的变化,各水库发电量占梯级总发电量比重略有变化,其中洪家渡水库所占比重随来水减少而不断减少,从来水频率p=10%的5.62%减少到p=90%的4.82%,减少幅度为0.8%；而索风营、乌江渡水库占梯级比重随来水减少则不断增加,其中索风营从来水频率p=10%的6.04%增加到p=90%的6.29%,增加幅度为0.25%,乌江渡从来水频率p=10%的13.56%增加到p=90%的14.46%,增加幅度为0.92%；构皮滩水位变化略有波动,整体呈现减少趋势；其余各库中,东风随来水增加呈增加趋势,思林与沙沱水库随来水的变化波动,趋势但并不明显。

3.2 优化调度

选取不同频率的来水,各库始末水位相同与常规调度一致,以梯级发电量最大为目标,采用大系统分解协调方法,计算乌江干流7库96点日调度,结果如表3所示。从优化调度结果可以看到出：

(1)构皮滩仍然占梯级发电比重最大,而且比常规占梯级比重略微提高,各频率来水条件下均超过34%；洪家渡仍旧最小,但是比重有所提高,均超过5.1%。与常规调度相比,东风、索风营水库发电量占梯级总量比重略有增加,乌江渡、沙沱有所减少,思林没有太大变化。

(2)随着来水的变化,优化调度的各水库发电量占梯级发电量比重略有变化,其中洪家渡水库所占比重随来水减少而不断减少,从来水频率p=10%的5.89%减少到p=90%的5.10%,减少幅度为0.79%,与常规调度相差不多；索风营、乌江渡水库占梯级比重随来水减少不断增加,其中索风营从来水频率p=10%的6.64%增加到p=90%的6.81%,增加幅度为0.17%,比常规调度增幅减少,乌江渡从来水频率p=10%的12.86%增加到p=90%的13.88%,增加幅度为1.02%,增幅略高于常规调度；其余各库中,东风、思林随来水增加呈增加趋势,沙沱呈减少趋势,构皮滩水库随来水的变化波动,趋势并不明显。

3.3 优化调度与常规调度对比分析

优化调度与常规调度的结果无法直接用来比较,因为两种方法的梯级总来水量是不同的,原因是因为短期调度考虑了水流时滞的影响。在乌江干流梯级水库中,相邻两库最大水流时滞时间为3小时,最小也需要1小时,因此水流时滞在乌江短期日优化调度中是一个不容忽视的因素。水流时滞对短期日优化调度的影响集中体现在水量平衡方面,具体地说就是,由于水流滞时的影响,使得上级电站前一日最时间内的流量参与下一级电站次日的水量平衡；同时本级电站当日最后时间内的流量参与下级电站次日的水量平衡。因此,上游电站的下泄流量、区间入流量以及进入下游水库的流量在一个时段甚至一日内,并不是平衡的。其中任一级电站的日发电水可视为两部分组成。一部分为当日水量,另一部分为前一日的水量。

但是为了能够直观的分析说明优化调度与常规调度的差异,做以下处理：①以梯级来水较少的优化调度为基准,减少常规梯级来水到与优化调度相同。②同倍比缩放常规调度除洪家渡以外其他各水库的来水与发电量。

不同频率来水的优化调度下梯级发电量与经过处理的不同频率来水的常规调度下梯级发电量结果如表4所示。通过表4可以看出,随着区间来水增大,发电量增加,但并不是来水越大,优化的效果越明显。当区间来水频率为50%的时候,优化结果最为明显,达到1.22%,区间来水频率为10%的时候优化效果最差,这是因为当来水较大的时候,水库的水位变幅减小,优化能力减弱。

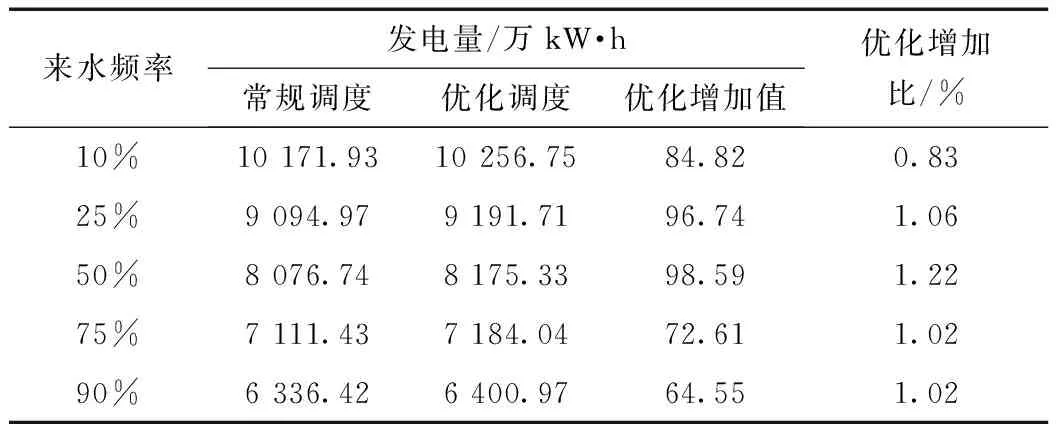
表4 不同频率区间来水的梯级常规与优化调度发电量比较

以区间来水频率为50%为例,详细分析各水库在梯级水库发电所占比重和优化效果，结果见表5。由表5可以看到,沙沱和乌江渡优化效果最差,小于常规调度,其他电站均优于常规调度,其中以索风营最为明显,达到10.82%,其次为乌江渡8.04%,构皮滩3.47%,思林不是很明显只有1.03%,整个梯级发电量优化调度较常规优化1.22%,从上面的优化结果中可以发现：

(1)两个具有多年调节性能的水库水位变化最小,洪家渡与构皮滩水位变化只有0.03 m；调节性能较弱的水库水位变化较大,其中以库容最小的索风营水位变化最大,达到1.8 m,可以认为水位变化幅度与库容大小直接相关。

(2)从水位变化过程来看,具有日调节以上性能的水库,除了东风在前期因为受洪家渡放水的影响,水位略微抬升,其他3座水库均前期降低水位,后期抬高水位,3座日调节性能水库均采取前期蓄水后期放水原则。

表5 P=50%的常规与优化调度比较

4 结 论

本文应基于大系统分解协调算法对发电量最大模型进行求解,其中洪家渡水库所占比重随来水减少而不断减少,索风营、乌江渡水库占梯级比重随来水减少不断增加,东风、思林随来水增加呈增加趋势,沙沱呈减少趋势,构皮滩水库随来水的变化波动,趋势并不明显。并于不同频率来水的常规算法进行比较,当区间来水频率为50%的时候,优化结果最为明显,达到1.22%,区间来水频率为10%的时候优化效果最差。最后对50%频率来水的发电过程进行了分析,从水位变化过程来看,具有日调节以上性能的水库,除了东风在前期因为受洪家渡放水的影响,水位略微抬升,其他3座水库均前期降低水位,后期抬高水位,3座日调节性能水库均采取前期蓄水后期放水原则。

[1] 郭乐, 徐斌. 三峡梯级水库群联合优化调度增发电量分析[J]. 水力发电, 2016, 42(12): 90- 93．

[2] 李克正, 武见, 谢维, 等. 基于优化调度规律挖掘的水库调度运用方案研究[J]. 水力发电, 2015, 41(12): 96- 100．

[3] 钟平安, 张金花, 徐斌, 等. 梯级库群水流滞后性影响的日优化调度模型研究[J]. 水力发电学报, 2012, 31(4): 34- 38．

[4] 刘烨, 钟平安. 基于多重迭代算法的梯级水库群调度图优化方法[J]. 水利水电科技进展, 2015, 35(1): 85- 88 ．

[5] 张阳, 钟平安, 徐斌, 等. 基于廊道约束的水库调度图优化遗传算法[J]. 水利水电科技进展, 2014, 34(6): 13- 17．

[6] 张双虎. 梯级水库群发电优化调度的理论与实践—以乌江梯级水库群为例[D]. 西安: 西安理工大学, 2007．

[7] VALENZUELA J, MAZUMDAR M. A probability model for the electricity price duration curve under an oligopoly market[J]. IEEE Transactions on Power Systems, 2005, 20(3): 1250- 1256．

[8] ELFERCHICHI A, GHARSALLAH O, NOUIRI I, et al. The genetic algorithm approach for identifying the optimal operation of a multi-reservoirs on-demand irrigation system[J]. Bio-systems Engineering, 2009, 102(3): 334- 344．

[9] AFSHER M H, MOEINI R. Partially and fully constrained ant algorithms for the optimal solution of large scale reservoir operation problems[J]. Water Resour Manage, 2008, 22(12): 1835- 1857．