SH0导波在粘接结构中传播时的相位变化1)

丁俊才 吴 斌何存富

(北京工业大学机械工程与应用电子技术学院，北京100124)

SH0导波在粘接结构中传播时的相位变化1)

丁俊才 吴 斌2)何存富

(北京工业大学机械工程与应用电子技术学院，北京100124)

对粘接结构进行超声导波无损检测与评估是一个有挑战性的前沿性课题.针对此问题，研究了SH0导波在界面为理想连接的三层板状粘接结构中传播时的相位变化情况.首先基于波传播的控制方程，建立了粘接结构中反射和透射SH0导波相对于入射SH0导波的相位差解析模型.然后利用数值模拟计算了铝/环氧树脂/铝粘接结构中反射和透射SH0导波的相位差曲线.最后分析了入射角度和频厚积的变化对反射和透射SH0导波相位差的影响.结果表明，对于具体的粘接结构，反射和透射SH0导波在其中传播时的相位差变化主要依赖于入射角度、频率等参数.在特定的频厚积下，当声波水平入射时，反射和入射SH0导波同相位.无论入射角度为多大，随着频厚积的增大，反射SH0导波的相位差曲线均会产生周期性谐振.对于透射SH0导波，当声波垂直入射时，其相位差曲线的改变无规律可循；但是随着入射角度逐渐增大，透射SH0导波的相位差曲线逐渐变规则.所得结果可为实验时研究板状粘接结构中SH0导波的传播特性以及提取SH0导波回波中的有用信息和定位提供一定的理论指导.

粘接结构,SH0导波,相位差,反射和透射,周期性谐振

引言

粘接结构因具有比强度、比模量高，以及密封、减振等优越性能，在机械、建筑、医疗、电力、航空航天等领域被广泛应用[1-2].为保证粘接结构在使用过程中的机械强度与稳定性，必须要对粘接界面的力学性能进行无损检测与评估[3].因此，针对粘接结构界面力学行为及其表征技术的研究具有一定的学术意义和应用价值[4].超声导波由于具有能量衰减小、检测效率高、传播距离远以及能携带更多的界面局部特征信息等优点，目前已成为粘接结构无损检测应用最为广泛的技术之一[5].

Deng等[6]采用半解析有限元方法分析了具有锥形粘接层的粘接结构中的导波传播特性.Cerniglia等[7]利用3D模拟和实验的方法研究了多层粘接结构中的导波传播.然而，相对于其他导波而言，SH导波(也可简称为SH波)由于具有频散小、易激发、灵敏度高，且可以实现高频小厚度检测等优势，在针对粘接以及其他结构的检测中更受关注[8-9].Crom等[10]通过数值模拟得到了铝/复合板粘接结构中的SH波频散曲线，分析了铝板和复合板的厚度、剪切模量等参数对SH波相速度的影响.Banerjee[11]从理论上分析了粘接结构中的SH波传播模式，研究发现，垂直激发时响应信号被一阶反对称模态所控制. Chaudhary等[12]推导了自增强弹性层处于两均匀半无限固体之间的“三明治”结构中平面SH波的反射和透射系数表达式.Dravinski等[13]和Sheikhhassani等[14]利用边界积分法研究了多层结构中SH波的频散特性.Castaings[15]利用有限元和实验的方法研究了处于不同界面质量的铝/树脂玻璃/铝搭接结构中SH波的传播，研究表明，SH0导波对界面质量的变化非常敏感.Predoi等[16]基于SH波通过分析粘接界面强度的降低研究了粘接层厚度的变化规律.Wang等[17-18]分析了SH波在两层结构中传播时的相位变化.Yew等[19]利用SH波评估了粘接结构粘接层的质量，研究表明，粘接结构中SH波二阶模态的截止频率主要依赖于粘接层的厚度和力学性能.Ding等[20]基于弹簧模型法推导了弱粘接结构中SH0导波的反射和透射系数表达式，研究了弱界面和SH0导波的相互作用.

刘福平等[21]利用SH波在层界面反射系数的附加相角研究了SH波Goos-Hanchen效应所引起的横向偏移.代海涛等[22]基于传递矩阵二维谱分析了复合材料层合板中稳态SH波的频散特性.徐红玉等[23]讨论了多层弹性介质中平面SH波通过弹性夹层时的传播特性，求得了透射波和反射波振幅的解析表达式.龚育宁[24]研究了具有滑移界面的两层结构中SH波的反射和透射特性，研究表明，若入射波的强度无法使接触面发生粘着，那么接触面上无透射现象.魏唯一等[25]讨论了初应力对周期压电/压磁层状结构中SH波传播特性的影响.郭智奇等[26]研究了层状黏弹性介质中SH波的反射和透射情况，得到了二维黏弹性平面的SH波解.杜建科等[27]基于线弹性理论讨论了功能梯度压电材料层状结构中的SH波，结果指出，适当的材料梯度分布可使SH波倾向于沿覆盖层表面传播.杨理践等[28]分析了有界双层结构中SH波的频散特性.余嘉顺等[29]精确模拟了SH波在表面多层介质中的传播，得到了具有特定波形和传播方向组合的任意SH波声场.艾春安等[30]给出了粘接界面层多孔缺陷微观结构的界面数学模型，得到了SH波在“三明治”结构中传播的频散方程，分析了孔隙度的变化对SH0导波传播速度的影响.

综上可见，许多学者采用不同的方法结合超声SH波对多层结构开展了研究并取得了相应的成果.但是分析发现，以上文献大多针对的是层状结构中SH波的多模态或频散特性，未见有关于多层板状粘接结构中SH波传播时单个或多个模态相位变化情况的讨论.对超声导波传播过程中的相位变化进行研究，有助于提取其回波中的有用信息和定位[31].与SH波其他非零阶模态(例如SH1,SH2,SH3,··)不同的是，无论是在单层还是多层板状结构中传播的SH0导波均无频散现象，也即其声弹性应力响应不受入射频率的影响.另外，由于在各向同性弹性固体板介质中SH波和SV横波、纵波是解耦的，因此当SH0导波单独入射时，结构中不会形成SV横波和纵波；类似地，若采用SV横波或纵波入射，在波结构上也可以认为SH0导波对于板中应力检测是无声弹性效应的[32].SH0导波的这些特性决定了其比SH波其他非零阶模态更适合于单层或多层板状结构的检测.

针对上述问题,作为理论上的补充，本文以具有非频散特性的SH导波的最低阶模态(即SH0导波)为例，研究三层板状粘接结构中SH0导波在传播时的相位变化问题.首先在界面处于理想(也称刚性或完好)连接的情况下，从理论上得到粘接结构中SH0导波的反射和透射系数表达式，进而由此两个系数表达式分别导出反射和透射SH0导波相对于入射SH0导波(下文若有提及反射或透射SH0导波相位差之处均指反射或透射SH0导波相对于入射SH0导波的相位差)的相位差(即SH0导波传播过程中因界面存在而产生的附加相角)解析表达式；接着利用数值模拟计算粘接结构中反射和透射SH0导波的相位差曲线；最后分析声波入射角度或频厚积的变化对反射和透射SH0导波相位差的影响.

1 理论分析

图1所示为SH波传播示意图.将笛卡尔坐标系的y轴置于三层板状粘接结构的上界面(界面1)，板厚沿x方向.假设半无限固体介质1和介质3分别为粘接结构的上、下基体，介质2是厚度为h的粘接层，介质1～介质3均为各向同性弹性固体介质.同时，忽略波传播的非线性效应，不考虑SH波在结构中传播时的衰减.图中SHi1为入射SH波；SHt2和SHt3分别为粘接层和基体3中的透射SH波；SHr1和SHr2分别为基体1和粘接层中的反射SH波.α为粘接层中SH波的传播角；θ和β分别为SH波在基体1中的入射(或反射)角和在基体3中的透射角.由于SH波在各向同性弹性固体介质中传播时不发生波型转换，因此在介质1～介质3中仅存在SH波.若令角频率为ω的平面简谐SH波从上基体1入射到多层粘接结构，依据Snell定律，入射波和所有的反射或透射波的波矢量沿y方向的分量都相等.

图1 粘接结构中SH波传播模式Fig.1 SH wave propagation model in bonding structure

容易知道，各向同性弹性固体介质中，平面简谐SH波只在z方向上的位移分量不为零，即ux=uy=0(ux和uy分别为x和y方向上的位移分量).因此，SH波的Navier控制方程可写为[33]

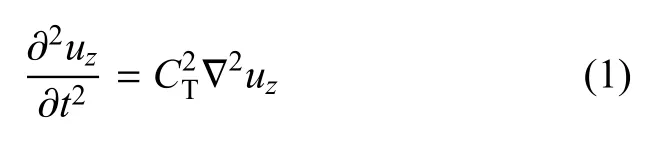
式(1)中，uz为z方向上的位移分量；t为时间；∂和∂2分别为一阶和二阶偏微分算子；∇2为二阶Laplace算子为横波速度，这里µ和ρ分别为介质的剪切模量和密度.

如图1所示，这里将基体1、粘接层和基体3中沿着z方向的位移分量(记为uz1,uz2和uz3)分别写成以下形式

式(2)中，k和ω分别为波数和角频率.之所以选取这种解的形式，主要是由于它代表波动沿着y方向传播(由指数项表示)，且在x方向有确定的分布(由g1(x),g2(x)和g3(x)给出).一般地，实际的物理位移场是式(2)右边项的实部.

结合式(1)和式(2)可知，实际上g1(x),g2(x)和g3(x)分别是下列3个微分方程的解

式(3)中

这里，c=ω/k为相速度，CT(1),CT(2)和CT(3)分别为介质1～介质3中的横波速度.诚如前文所言，入射波、反射波与透射波的波矢量沿界面的分量相等，因此在界面1和界面2处分别有

在式(4)的基础上，可以很容易写出式(3)的位移通解

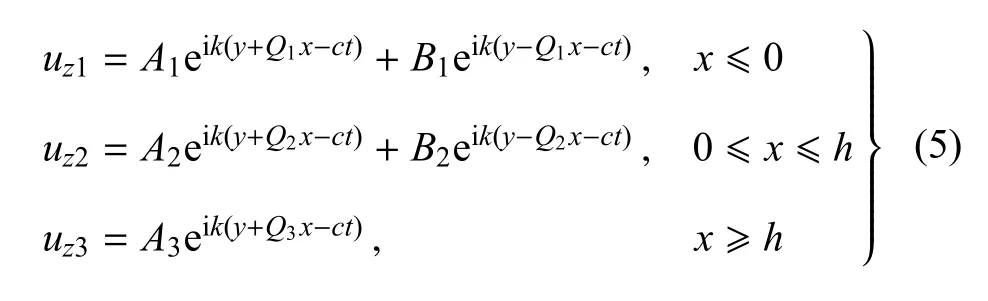
式(5)中，A1和B1分别为基体1中入射和反射SH波的幅值；A2和B2分别为粘接层中透射和反射SH波的幅值；A3为基体3中透射SH波的幅值.

若界面1和界面2为理想连接，那么界面上的切向位移和应力连续，因此界面1和界面2上的连接条件可分别写为

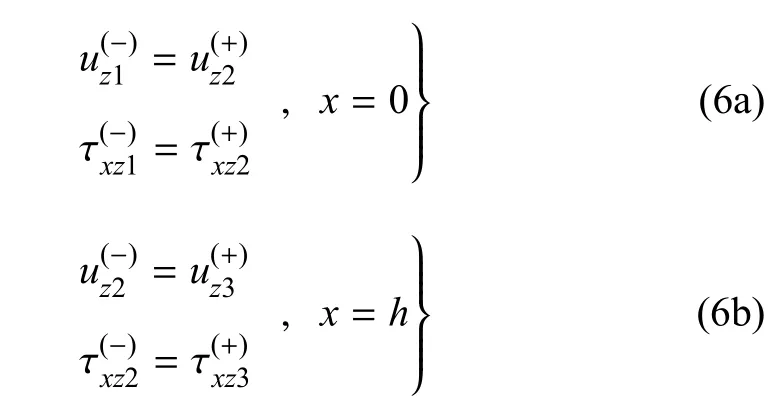
式(6)中，符号“+”和“-”分别表示界面的上侧与下侧；τxz1,τxz2,τxz3分别为基体1、粘接层和基体3中沿着z方向的切应力分量，且

式中，µ1,µ2和µ3分别为基体1、粘接层和基体3的剪切模量.将式(5)、式(7)和界面连接条件式(6)相结合并经过一定的运算，最后可以得到粘接结构中SH0导波的反射和透射系数表达式

这里假设δ=δ1-δ2,δ′=δ3-δ2，那么δ,δ′分别为粘接结构中SH0导波因被粘接界面反射、透射而产生的附加相位角，也即反射、透射SH0导波相对于入射SH0导波的相位差.

2 数值计算与结果分析

基于上述模型，利用Mathematica软件编写相应的程序计算粘接结构中反射或透射SH0导波在传播过程中相位差的变化曲线.本文选取均匀无杂质、无缺陷的铝板作为粘接结构的基体材料，环氧树脂为粘接剂，其物理参数见表1.

表1 常见材料的物理性质Table 1 Physical properties of common materials

2.1 入射角度与相位差的关系

图2为SH0导波以不同角度入射的情况下，铝/环氧树脂/铝粘接结构中反射与透射SH0导波相对于入射波的相位差变化情况.图中SH0导波的频率取1MHz.由于实际工业生产中常用粘接结构的粘接层厚度通常为几十到几百微米，因此本节将粘接层的厚度固定在0.2mm.诚然，频率和粘接层厚度也可取满足条件的其他值.

图2 入射角度对SH0导波相位差的影响Fig.2 The ef f ect of incident angle on the phase-dif f erence of SH0guided wave

由图2可知，入射角度的改变对反射和透射SH0导波的传播相位差有一定影响.反射和透射SH0导波相对于入射波而言，相位差变化的区别较为明显，并且从整体上讲，透射SH0导波在传播时相位差的变化大于反射SH0导波.对于反射SH0导波，与入射波相比，相位差总体变化不大且最大不超过0.3rad.当声波的入射角度小于82°，相位差随着入射角度的增大缓慢增大；当入射角位于82°～90°之间，相位差急剧缩小.尤其当入射角为90°时，反射和入射SH0导波同相位.对于透射SH0导波，当入射角分别小于和大于48.3°时，透射SH0导波的传播相位相对于入射波基本保持不变，相位差分别维持在1.1rad和-1.95rad左右.然而当入射角处于48.3°附近，透射SH0导波的相位差发生了快速且剧烈的“突变”.之所以会产生此种“突变”现象，除了与SH0导波本身的波结构有关以外，还与粘接结构的材料参数以及声波的频率等有关.若波型、材料参数和频率等改变，那么图2(b)中相位差曲线发生“突变”的位置也会有所变化.

2.2 频厚积与相位差的关系

针对粘接结构的检测，频厚积一直是重要和关键的参数.就超声检测中常用的兆赫兹脉冲激励而言，其相对带宽通常在50%～80%之间，检测的频厚积往往不超过 5MHz·mm. 因此，本节将在0～5MHz·mm的频厚积范围内展开研究.图3～图5所示分别为铝/环氧树脂/铝粘接结构在SH0导波以特定角度(0°,30°或60°)入射时，频厚积的变化对反射或透射SH0导波相位差的影响.

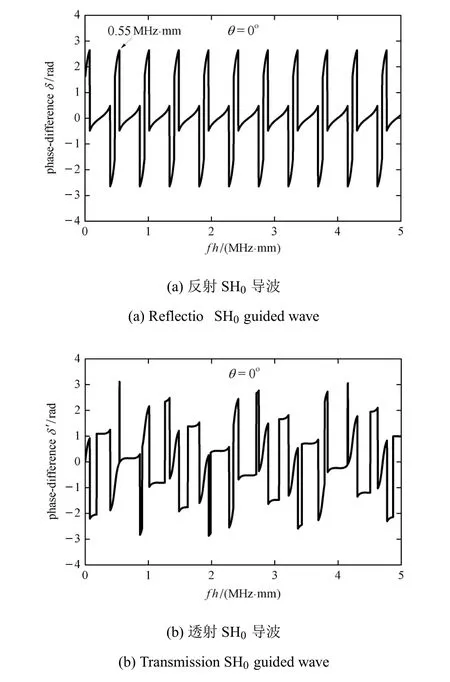
图3 入射角为0°时频厚积对SH0导波相位差的影响Fig.3 The ef f ect of frequency-thickness product on the phase-dif f erence of SH0guided wave when the incident angle is 0°

图4 入射角为30°时频厚积对SH0导波相位差的影响Fig.4 The ef f ect of frequency-thickness product on the phase-dif f erence of SH0guided wave when the incident angle is 30°

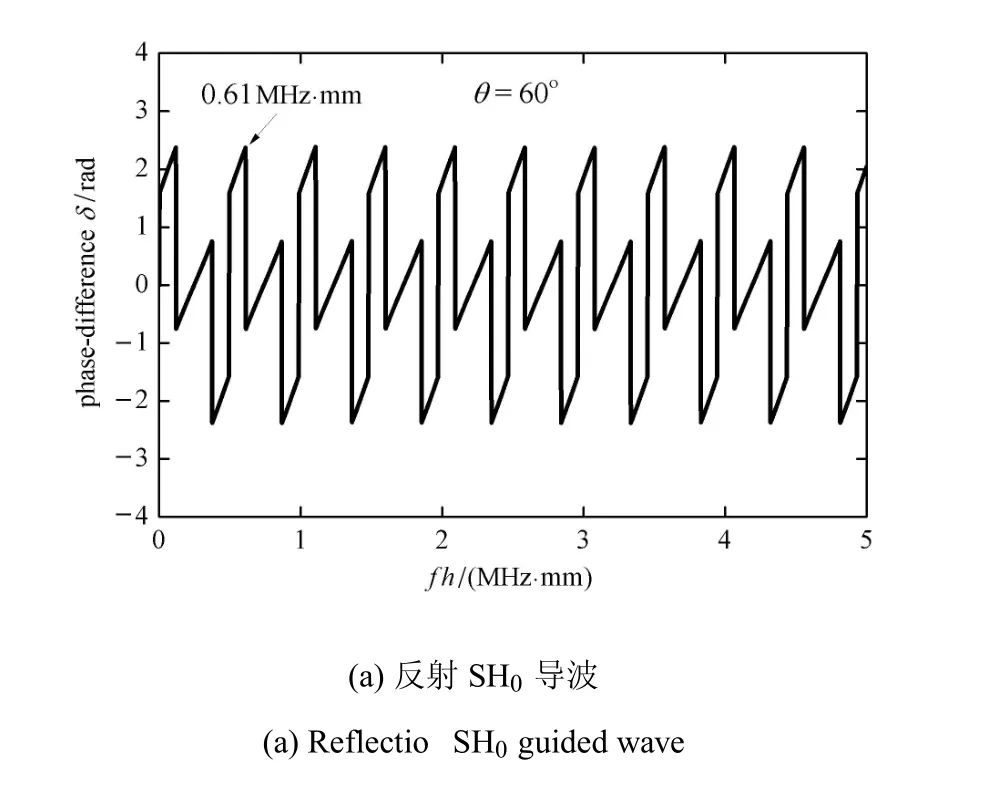
图5 入射角为60°时频厚积对SH0导波相位差的影响Fig.5 The ef f ect of frequency-thickness product on the phase-dif f erence of SH0guided wave when the incident angle is 60°

图5 入射角为60°时频厚积对SH0导波相位差的影响(续)Fig.5 The ef f ect of frequency-thickness product on the phase-dif f erence of SH0guided wave when the incident angle is 60°(continued)

出于撰写简洁性考虑，本节仅以图3和图5为例进行分析.当声波垂直入射，反射SH0导波(图3(a))的相位差曲线出现了规则的以0.55MHz·mm为周期的谐振，并且曲线的极大值和极小值点处的幅值分别保持为±2.64rad不变.在所有极大值和极小值点的两侧，反射SH0导波的相位差发生了较为剧烈的转变.当声波的入射角度增大到60°(图5(a))，反射SH0导波相位差曲线的谐振现象依然存在，但是与垂直入射相比，其谐振周期增大了11%；另外，极大值和极小值点处的幅值分别下降和上升了9.9%.与反射SH0导波不同的是，对于透射SH0导波，当声波垂直入射(图3(b))，其相位差曲线与反射时相比稍显“混乱”无规律；当入射角增大到60°(图5(b))，透射SH0导波的相位差曲线反而变得较为规则.除了上述现象，再次观察图3～图5可以发现，无论声波的入射角度和频厚积为多大，反射和透射SH0导波相位差曲线的极大值和极小值点处的幅值均不超过±πrad.

2.3 频率、粘接层厚度与相位差之间的三维关系

图6～图9分析了声波入射频率、粘接层厚度和反射或透射SH0导波相位差之间的三维关系.对应于前文，这里图6和图8中SH0导波的入射角取0°；图7和图9中SH0导波的入射角取60°，图中颜色的深浅表示相位差幅值的大小.这些三维图清晰地显示出了相位差的变化趋势，如图6(b)中箭头所指的类似于曲线的部分，其中蓝颜色和红颜色线条分别表示反射SH0导波与入射波相位差的极小值和极大值点.如2.2节所言，对于反射SH0导波，当入射角取0°或60°时相位差的变化规则且有规律.对比图6(b)与图7(b)可以发现，入射角度越大，蓝颜色和红颜色线条的宽度越宽，表明曲线的谐振周期在增大.类似地，对于透射SH0导波(图8和图9)，当入射角为0°，相位差曲线的改变“杂乱无章”毫无规律可循；但是当入射角达到60°，曲线的变化较为规则.

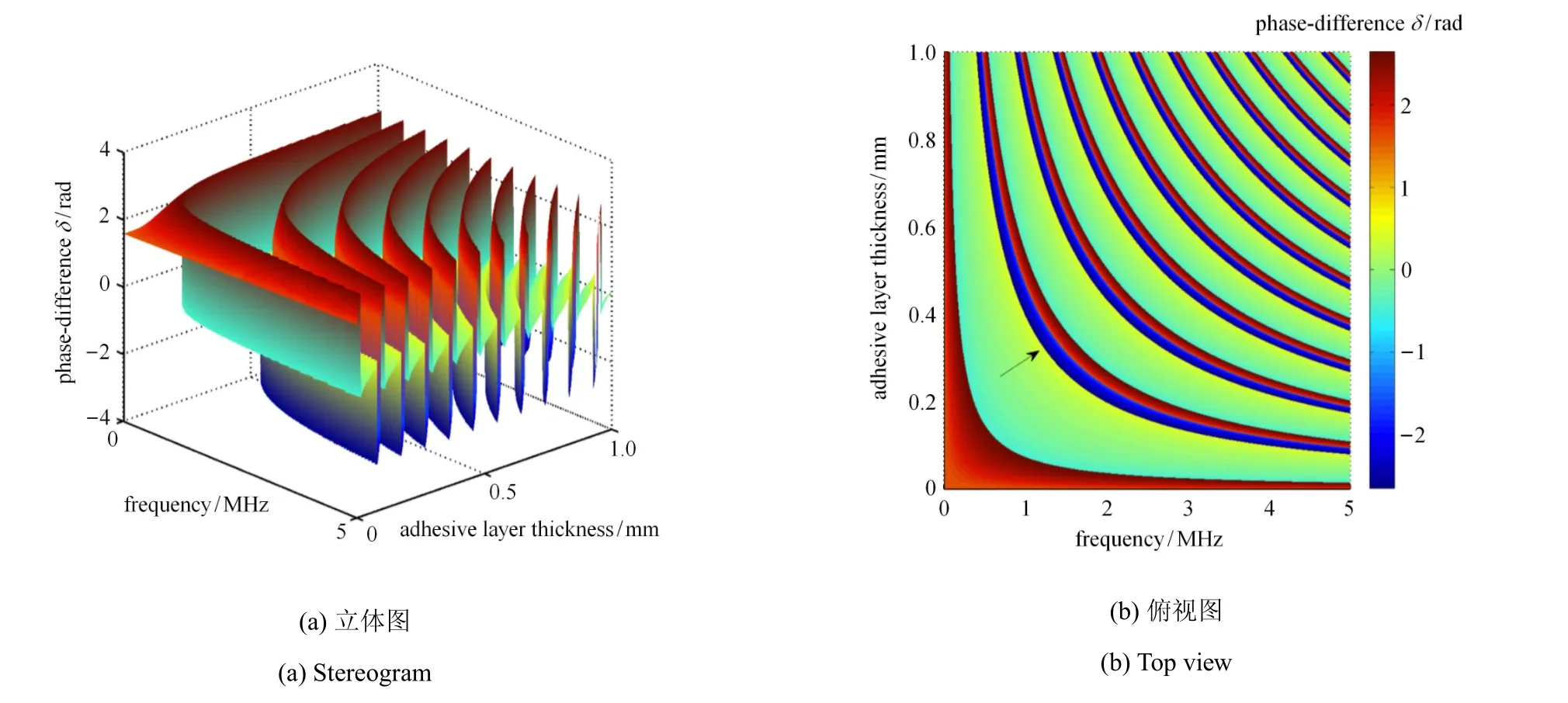
图6 入射角为0°时频率、粘接层厚度与反射SH0导波相位差之间的关系Fig.6 The relationship between the frequency,the thickness of adhesive layer and the phase-dif f erence of reflectio SH0guided wave when the incident angle is 0°

图7 入射角为60°时频率、粘接层厚度与反射SH0导波相位差之间的关系Fig.7 The relationship between the frequency,the thickness of adhesive layer and the phase-dif f erence of reflectio SH0guided wave when the incident angle is 60°

图8 入射角为0°时频率、粘接层厚度与透射SH0导波相位差之间的关系Fig.8 The relationship between the frequency,the thickness of adhesive layer and the phase-dif f erence of transmission SH0guided wave when the incident angle is 0°

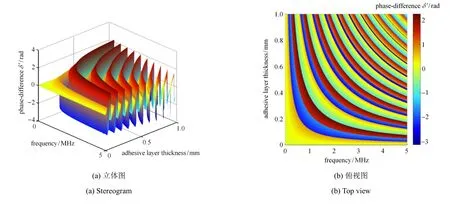
图9 入射角为60°时频率、粘接层厚度与透射SH0导波相位差之间的关系Fig.9 The relationship between the frequency,the thickness of adhesive layer and the phase-dif f erence of transmission SH0guided wave when the incident angle is 60°

3 讨论和结论

对粘接结构中超声导波传播问题的研究一直受到重视.作为理论补充，我们讨论了界面为理想连接的三层板状粘接结构中SH0导波在传播时的相位变化情况，得到以下结论：

(1)本文在SH0导波入射的情况下，基于波传播的控制方程，从理论上推导了粘接结构中反射和透射SH0导波相对于入射波的相位差解析表达式.通过计算证实了所推公式的正确性.

(2)对于具体的粘接结构，反射和透射SH0导波在其中传播时相位差的变化主要依赖于入射角度、频率等参数.无论声波的入射角度为多大，随着频厚积的增大，反射SH0导波与入射波的相位差曲线均会出现规律的周期性谐振.对于透射SH0导波，当声波垂直入射时，其相位差曲线的改变无任何规律可循；但是随着声波入射角度的增大，透射SH0导波的相位差曲线逐渐由不规则变规则.无论SH0导波的入射角度和频厚积为多大，反射和透射SH0导波相位差曲线的极大值和极小值点处的幅值均不会超过±π rad.本文的研究成果可为具体实验时提取SH0导波回波中的有用信息和定位提供较好的理论指导.

1 Wu B,Ding JC,He CF,et al.Wave propagation in water-immersed adhesive structure with the substrates of finit thickness.NDT&E International,2016,80：35-47

2 MassereyB,RaemyC,FrommeP.High-frequencyguidedultrasonic waves for hidden defect detection in multi-layered aircraft structures.Ultrasonics,2014,54(7)：1720-1728

3 Zhang KS,Zhou ZG,Zhou JH,et al.Characteristics of laser ultrasound interaction with multi-layered dissimilar metals adhesive interface by numerical simulation.Applied Surface Science,2015, 353：284-290

4 Moreno MCS,Cela JJL,Vicente JLM,et al.Adhesively bonded joints as a dissipative energy mechanism under impact loading.Applied Mathematical Modelling,2015,39(12)：3496-3505

5 Kundu S,Manna S,Gupta S.Propagation of SH-wave in an initially stressed orthotropic medium sandwiched by a homogeneous and an inhomogeneous semi-infinit media.Mathematical Methods in the Applied Sciences,2015,38(9)：1926-1936

6 Deng QT,Yang ZC.Propagation of guided waves in bonded composite structures with tapered adhesive layer.Applied Mathematical Modelling,2011,35(11)：5369-5381

7 Cerniglia D,Pantano A,Montinaro N.3D simulations and experiments of guided wave propagation in adhesively bonded multilayered structures.NDT&E International,2010,43(6)：527-535

8 Graham JW,Lee JK.Reflectioand transmission from biaxially anisotropic-isotropic interfaces.Progress in Electromagnetics Research,2013,136：681-702

9 Vajari DA,Sørensen BF,Legarth BN.Ef f ect of fibe positioning on mixed-mode fracture of interfacial debonding in composites.International Journal of Solids and Structures,2015,53：58-69

10 Crom LB,Castaings M.Shear horizontal guided wave modes to in-fer the shear stif f ness of adhesive bond layers.Journal of the Acoustical Society of America,2010,127(4)：2220-2230

11 Banerjee S.Theoretical modeling of guided wave propagation in a sandwich plate subjected to transient surface excitations.International Journal of Solids and Structures,2012,49(23-24)：3233-3241

12 Chaudhary S,Kaushik VP,Tomar SK.Reflectio/transmission of plane SH wave through a self-reinforced elastic layer between two half-spaces.Acta Geophysica Polonica,2004,52(2)：219-235

13 Dravinski M,Sheikhhassani R.Scattering of a plane harmonic SH wave by a rough multilayered inclusion of arbitrary shape.Wave Motion,2013,50(4)：836-851

14 Sheikhhassani R,Dravinski M.Scattering of a plane harmonic SH wave by multiple layered inclusions.Wave Motion,2014,51(3)：517-532

15 Castaings M.SH ultrasonic guided waves for the evaluation of interfacial adhesion.Ultrasonics,2014,54(7)：1760-1775

16 Predoi MV,Kettani MEC,Leduc D,et al.Use of shear horizontal waves to distinguish adhesive thickness variation from reduction in bonding strength.Journal of the Acoustical Society of America, 2015,138(2)：1206-1213

17 Wang AL,Liu FP.The phase shift of reflectio and refraction of SH-wave at an interface of two media.Advanced Materials Research, 2014,983：388-391

18 Wang AL,Liu FP.The lateral shift of refraction SH-wave on an interface of two media.Advanced Mechanics and Materials,2014, 551：580-582

19 YewCH,WengXW.UsingultrasonicSHwavestoestimatethequality of adhesive bonds in plate structures.Journal of the Acoustical Society of America,1985,77(5)：1813-1823

20 Ding JC,Wu B,He CF.Reflectio and transmission coefficients of the SH0mode in the adhesive structures with imperfect interface.Ultrasonics,2016,70：248-257

21 刘福平,王安玲,李瑞忠等.全反射SH地震波的Goos-Hanchen效应动校正时差.地球物理学报,2009(8)：2128-2134(Liu Fuping, Wang Anling,Li Ruizhong,et al.The influenc on normal moveout of total reflecte SH-wave by Goos-Hanchen ef f ect at an interface of strata.Chinese Journal of Geophysics,2009(8)：2128-2134(in Chinese))

22 代海涛,程伟.压电复合材料层合结构中的SH波.复合材料学报,2007,24(1)：179-184(Dai Haitao,Cheng Wei.SH wave in piezoelectric composite layered structure.Acta Materiae Compositae Sinica,2007,24(1)：179-184(in Chinese))

23 徐红玉,陈殿云,杨先建等.弹性介质中平面SH波通过弹性夹层时的传播特性.岩石力学与工程学报,2003,22(2)：304-308(Xu Hongyu,Chen Dianyun,Yang Xianjian,et al.Propagation characteristics of plane SH wave passing through elastic interlining in elastic medium.Chinese Journal of Rock Mechanics and Engineering, 2003,22(2)：304-308(in Chinese))

24 龚育宁.SH波在滑动接触面上的反射与折射.固体力学学报, 1987,8(2)：174-178(Gong Yuning.The reflectio and refraction of SH-waves at a slipping unilateral interface.Chinese Journal of Solid Mechanics,1987,8(2)：174-178(in Chinese))

25 魏唯一,刘金喜,方岱宁.初应力对周期压电/压磁层状结构中SH波传播特性的影响.工程力学,2010,27(11)：184-190(Wei Weiyi, Liu Jinxi,Fang Daining.Ef f ect of initial stress on the propagation characteristics of SH-waves in periodic piezoelectric-piezomagnetic layered structures.Engineering Mechanics,2010,27(11)：184-190 (in Chinese))

26 郭智奇,刘财,张凤琴.层状黏弹性介质中SH波的反射和透射问题.吉林大学学报(地球科学版),2005,35(增刊)：57-61(Guo Zhiqi,Liu Cai,Zhang Fengqin.Reflectio and transmission problem of SH waves in layered viscoelastic medium.Journal of Jilin University(Earth Science Edition),2005,35(Sup)：57-61(in Chinese))

27 杜建科,叶定友.功能梯度压电材料层状结构中的SH波.固体火箭技术,2005,28(2)：133-136(Du Jianke,Ye Dingyou.SH waves in laminated structure of functionally gradient piezoelectric material.Journal of Solid Rocket Technology,2005,28(2)：133-136(in Chinese))

28 杨理践,吕瑞宏,高松巍等.有界双层结构SH导波频散特性分析.沈阳工业大学学报,2016,38(3)：286-292(Yang Lijian,Lu Ruihong,Gao Songwei,et al.Analysis for frequency dispersion characteristics of SH guiding wave in bounded double layer structure.Journal of Shenyang University of Technology,2016,38(3)：286-292(in Chinese))

29 余嘉顺,贺振华.SH波在表面多层介质中传播的精确模拟.地震研究,2003,26(1)：14-19(Yu Jiashun,He Zhenhua.Precise modelling of SH wave propagation in subsurface multilayer media.Journal of Seismological Research,2003,26(1)：14-19(in Chinese))

30 艾春安,朱盛录,俞红博.横波检测粘接界面层多孔隙缺陷的数值分析.无损检测,2007,29(1)：16-19(Ai Chun’an,Zhu Shenglu, Yu Hongbo.Numeric analysis of the testing of porosity fl w on the adhesive layer with SH wave.Nondestructive Testing,2007,29(1)：16-19(in Chinese))

31 Rose JL.Ultrasonic Guided Waves in Solid Media.Cambridge：Cambridge University Press,2014

32 刘飞,吴斌,何存富等.弹性板中低阶导波模态声弹性效应分析.北京工业大学学报,2013,39(6)：823-827(Liu Fei,Wu Bin,He Cunfu,et al.Analysis of acoustoelastic ef f ect for low-order guided wave modes in elastic plate.Journal of Beijing University of Technology,2013,39(6)：823-827(in Chinese))

33 徐红玉,陈殿云,王钦亭.层合介质中平面SH波的传播.焦作工学院学报(自然科学版),2003,22(4)：320-323(Xu Hongyu,Chen Dianyun,Wang Qinting.Propagation of plan SH wave in laminated medium.Journal of Jiaozuo Institute of Technology(Natural Science),2003,22(4)：320-323(in Chinese))

THE PHASE SHIFT OF SH0GUIDED WAVE PROPAGATING IN BONDING STRUCTURE1)

Ding Juncai Wu Bin2)He Cunfu
(College of Mechanical Engineering and Applied Electronics Technology，Beijing University of Technology，Beijing100124，China)

It is a difficult and challenging subject for non-destructive testing and evaluation of adhesive structure by ultrasonic guided waves.For this issue,the phase shift of SH0guided wave transmitting in perfect connected trilaminar plate-like adhesive structure was researched.Firstly,the phase-dif f erence analytical model between the incident and transmission/reflectio SH0guided wave,which based on the control equation of wave propagation,was established.Then,the phase-dif f erence curves of reflectio/transmission SH0guided wave in aluminum/epoxy resin/aluminum adhesive structure were calculated by numerical simulation.Finally,the ef f ects of changes of incident angle and frequency-thickness product on the phase-dif f erence of reflectio/transmission SH0guided wave were analyzed.The results show that the changes of phase-dif f erence of reflectio/transmission SH0guided wave transmitting in adhesive structure mainly depend on the parameter as incident angle or frequency of acoustic wave,for the concrete bonding structure.The reflectio and incident SH0guided waves are in the same phase when the ultrasound is incident under a particular frequency-thickness product.Despite the angle of incidence,the phase-dif f erence curve of reflectio SH0guided wave shows periodic res-onance with the increasement of frequency-thickness product.For the transmission SH0guided wave,the change of the phase-dif f erence curve has no law to follow when the ultrasound is normal incident.But the phase-dif f erence curve changes from irregularity to regularity as the angle of incidence increase.The results obtained could provide the theory support for studying the propagation characteristics of SH0guided wave in plate-like bonding structure and information retrieving of echoed SH0guided wave and positioning during the experiment.

adhesive structure,SH0guided wave,phase-dif f erence,reflectio and transmission,periodic resonance

O347.4

A doi：10.6052/0459-1879-16-245

2016-09-05收稿，2016-10-28录用,2016-10-31网络版发表.

1)国家自然科学基金资助项目(11132002,11372016,51245001,51475012).

2)吴斌,教授,主要研究方向：波动力学及其应用和无损检测新技术.E-mail：wb@bjut.edu.cn

丁俊才,吴斌,何存富.SH0导波在粘接结构中传播时的相位变化.力学学报,2017,49(1)：202-211

Ding Juncai,Wu Bin,He Cunfu.The phase shift of SH0guided wave propagating in bonding structure.Chinese Journal of Theoretical and Applied Mechanics,2017,49(1)：202-211