一类广义Markov跳变随机反应扩散神经网络的稳定性研究
吕天石,甘勤涛
(军械工程学院基础部,河北 石家庄 050003)
一类广义Markov跳变随机反应扩散神经网络的稳定性研究
吕天石,甘勤涛
(军械工程学院基础部,河北 石家庄 050003)
广义神经网络; 反应扩散; Markov跳变; 随机干扰; 混合时滞; Lyapunov泛函
基于神经网络的基本变量,神经网络可分为局域神经网络和静态神经网络。ZHANG等[1]研究表明:只有当神经网络的负反馈矩阵和连接权矩阵是可交换的且连接权矩阵是非奇异矩阵时,局域神经网络与静态神经网络才是等同的。因此,局域神经网络的动力学分析结果并不能完全适用于静态神经网络,这在很大程度上限制了神经网络的理论研究和应用。此外,在神经网络的实现过程中,由于信号传输的速度以及放大器的切换速度皆有限,会不可避免地产生时滞,同时模拟神经网络的电子电路在不均匀的磁场环境下工作时也会产生电子的扩散效应。因此,有必要将时滞和反应扩散引入到神经网络中。
1 问题描述
设{rt,t≥0}为定义在完备概率空间(Ω,F,P)(带有满足通常条件的自然流{Ft}t≥0,即右连续性和F0包含所有P零测集)上取值于有限状态空间S={1,2,…,N}右连续的Markov过程,其转移概率为
(1)
考虑具有混合时滞的广义Markov跳变随机反应扩散神经网络,即
ζ,x)dt+W1(rt)f(W0y(t,x))dt+
W2(rt)f(W0y(t-τ,x))dt+W3(rt)×
σ(rt,t,y(t,x),y(t-τ,x))dω(t)。
(2)
通过分析式(2)可以看出:当W1(rt)=W2(rt)=W3(rt)=I时(I表示适当阶数的单位矩阵),为静态神经网络;当W0=I时,为局域神经网络。因此,式(2)可称为具有混合时滞的广义Markov跳变随机反应扩散神经网络,以下简称神经网络(2)。
(3)
初始条件
(4)
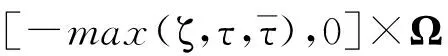
为方便证明,记rt=i时,A(rt)=Ai,W1(rt)=W1i,W2(rt)=W2i,W3(rt)=W3i。证明神经网络(2)的全局均方鲁棒渐近稳定性需要用到的假设、引理和定义如下:
假设1: 存在正定对角矩阵H,使得激励函数f(u)满足Lipschitz条件,即
fT(u)f(u)≤uTH2u。
假设2:存在正常数ρ1和ρ2,使得不等式
trace[σT(t)σ(t)]≤ρ1yT(t,x)y(t,x)+
ρ2yT(t-τ,x)y(t-τ,x)
成立,其中trace[·]表示矩阵的迹。
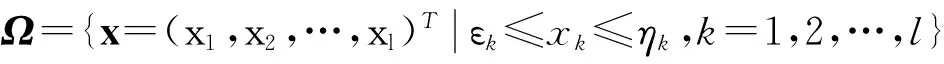
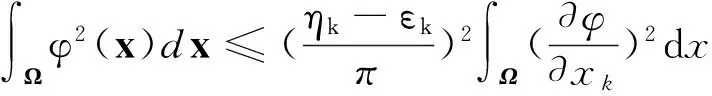
引理2[10]:对给定的向量x∈Rn,y∈Rn,存在ε>0,使得不等式
xTy+yTx≤εxTx+ε-1yTy
成立。
定义1[11]:如果存在正常数κ,使得不等式
2 主要结果
(5)
成立,则神经网络(2)是全局均方鲁棒渐近稳定的。式中:X 证明:对神经网络(2)构造正定的Lyapunov泛函 V[t,y(t,x),rt=i]=Vi[t,y(t,x)]= V1i[t,y(t,x)]+V2i[t,y(t,x)]+V3i[t,y(t,x)]+ V4i[t,y(t,x)]+V5i[t,y(t,x)], (6) 定义运算 (7) 式(6)、(7)中: V1i[t,y(t,x)]=∫ΩyT(t,x)Piy(t,x)dx; f(W0y(s,x))dsdθdx; W1(rt)f(W0y(t,x))dt+W2(rt)f(W0y(t- PiAiy(t-ζ,x)dx+∫ΩfT(W0y(t,x))W1iTPiy(t,x)dx+ ∫ΩyT(t,x)PiW1if(W0y(t,x))dx+∫ΩfT(W0y(t-τ,x))× W2iTPiy(t,x)dx+∫ΩyT(t,x)PiW2if(W0y(t-τ,x))dx+ Piσ(rt,t,y(t,x),y(t-τ,x)); (8) ∫ΩyT(t-ζ,x)Qy(t-ζ,x)dx; (9) ∫ΩyT(t-τ,x)Ry(t-τ,x)dx; (10) (11) f(W0y(s,x))μdsdx; (12) (13) 由边界条件(3)、格林公式及引理1,可知: -2∫ΩyT(t,x)PiDπy(t,x)dx。 (14) 根据引理2和假设1可知:存在正常数ε1和ε2,正定对角矩阵H1和H2,使得不等式 ∫ΩfT(W0y(t,x))W1iTPiy(t,x)dx+ ∫ΩyT(t,x)PiW1if(W0y(t,x))dx≤ ∫Ωε1fT(W0y(t,x))f(W0y(t,x))dx+ (15) ∫ΩfT(W0y(t-τ,x))W2iTPiy(t,x)dx+ ∫ΩyT(t,x)PiW2if(W0y(t-τ,x))dx≤ ∫Ωε2fT(W0y(t-τ,x))f(W0y(t-τ,x))dx+ ∫Ω[ε2yT(t-τ,x)W0TH22W0y(t-τ,x)+ (16) (17) 成立。 根据假设2可知:存在正常数ρ1和ρ2,使得不等式 ∫ΩσT(rt,t,y(t,x),y(t-τ,x))Piσ(rt,t,y(t,x), y(t-τ,x))dx≤∫Ωλi[ρ1yT(t,x)y(t,x)+ ρ2yT(t-τ,x)y(t-τ,x)]dx (18) 成立。 结合式(8)-(18),可得 ηT(t,x)Λη(t,x), 其中 因为Λ Λ+diag(κI,O,O,O) 则有 (19) 对式(19)两边取期望,可得 因此,结合定义1可知:神经网络(2)是全局均方鲁棒渐近稳定的,即定理1得证。 令y(t,x)=(y1(t,x),y2(t,x))T,考虑如下具有混合时滞的广义Markov跳变随机反应扩散神经网络,即 W1(rt)f(W0y(t,x))dt+W2(rt)f(W0y(t-τ,x))dt+ y(t-τ,x)]dω(t)。 (20) 其设定参数为 初始条件为 y1(t,x)=0.13{1+[t-τ(t)]/π}cos(x/π), y2(t,x)=0.21{1+[t-τ(t)]/π}cos(x/π), 其中(t,x)∈[-0.35,0]×Ω。 显然,H1、H2、P1、P2、Q和R是正定对角矩阵。因此,结合定理1可知式(20)可称为具有全局均方鲁棒渐近稳定的神经网络,以下简称“神经网络(20)”。 根据神经网络(20)及其设定参数和初始条件,模式i=1、2时神经网络的时间响应图分别如图1、2所示。可以看出:当选取满足线性矩阵不等式(5)的相应参数和激励函数时,具有Markov跳变参数、随机干扰和混合时滞的广义反应扩散神经网络是全局渐近稳定的。 图1 模式i=1时神经网络的时间响应图 图2 模式i=2时神经网络的时间响应图 笔者研究了一类具有混合时滞的广义Markov跳变随机反应扩散神经网络,利用Lyapunov稳定性理论得到了神经网络系统的全局鲁棒均方渐近稳定性判据,并通过数值模拟说明了所得结论的有效性。与以往结果相比,所得结果保守性较低,具有更广泛的适用范围,应用价值在一定程度上有所提高,给网络设计带来方便。 [1] ZHANG X,HAN Q.Global asymptotic stability for a class of gene-ralized neural networks with interval time-varying delays [J].IEEE transactions on neural networks,2011,22(8):1180-1192. [2] VIDHYA C,BALASUBRAMANIAM P.Stability of uncertain reaction-diffusion stochastic BAM neural networks with mixed delays and Markovian jumping parameters [J].Expert systems with applications,2012,39(3):3109-3115. [3] SHI G,MA Q.Synchronization of stochastic Markovian jump neural networks with reaction-diffusion terms [J].Neurocomputing,2012,77(1):275-280. [4] SHEN H,HUANG X,ZHOU J,et al.Global exponential estimates for uncertain Markovian jump neural networks with reaction-diffusion terms [J].Nonlinear dynamics,2012,69(1/2):473-486. [5] WANG Y,LIN P,WANG L.Exponential stability of reaction-diffusion high-order Markovian jump hopfield neural networks with time-varying delays [J].Nonlinear analysis:real world applications,2012,13(3):1353-1361. [6] ZHOU C,ZHANG H,ZHANG H,et al.Global exponential stability of impulsive fuzzy cohen-grossberg neural networks with mixed delays and reaction-diffusion terms [J].Neurocomputing,2012,91(2):67-76. [7] KAO Y,GUO J,WANG C,et al.Delay-dependent robust exponential stability of Markovian jumping reaction-diffusion cohen-grossberg neural networks with mixed delays [J].Neural proces-sing letters,2013,38(3):321-346. [8] MA Q,XU S,ZOU Y.Stability and synchronization for Markovian jump neural networks with partly unknown transition probabilities [J].Neurocomputing,2011,74(17):3404-3411. [9] ZHOU J,XU S,SHEN H,et al.Passivity analysis for uncertain BAM neural networks with time delays and reaction-diffusions [J].International journal of systems science,2013,44(8):1494-1503. [10] RAO R,ZHONG S,WANG X.Stochastic stability criteria with LMI conditions for Markovian jumping impulsive BAM neural networks with mode-dependent time-varying delays and nonlinear reaction-diffusion[J].Communications in nonlinear science & numerical simulation,2014,19(1):258-273. [11] LIU Y,WANG Z,LIU X.On global stability of delayed BAM stochastic neural networks with Markovian switching [J].Neural processing letters,2009,30(1):19-35. (责任编辑:尚菲菲) Research on Stability for a Class of Generalized Markovian Jumping Reaction-diffusion Neural Networks LÜ Tian-shi,GAN Qin-tao (Department of Fundamental Courses,Ordnance Engineering College,Shijiazhuang 050003,China) By constructing some suitable Lyapunov functionals and calculating the stochastic derivative of these Lyapunov functionals along neural networks using differential formula,the global mean square and asymptotic robust stability for a class of generalized Markovian jumping stochastic reaction-diffusion neural networks with mixed delays is discussed under Dirichlet boundary conditions.The obtained criteria not only depend on delays but also depend on diffusion coefficients and diffusion spaces.Finally,a numerical example is provided to show the validity of the obtained results criteria. generalized neural networks; reaction-diffusion; Markovian jump; stochastic perturbation; mixed delays; Lyapunov functionals 1672-1497(2017)01-0105-06 2016-11-20 国家自然科学基金资助项目(61305076) 吕天石(1990-),男,硕士研究生。 O175.13 A 10.3969/j.issn.1672-1497.2017.01.022



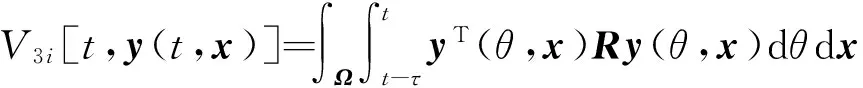
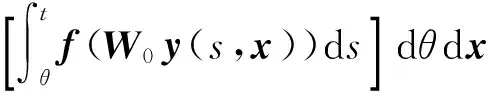
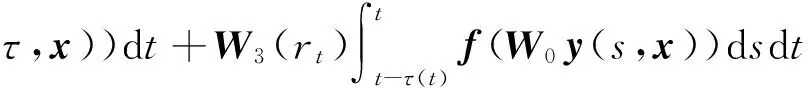






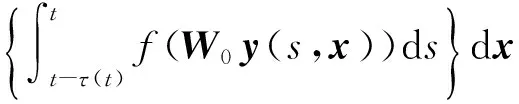

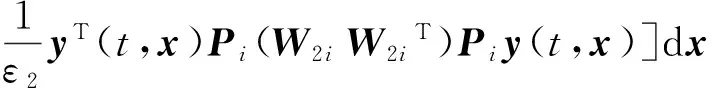

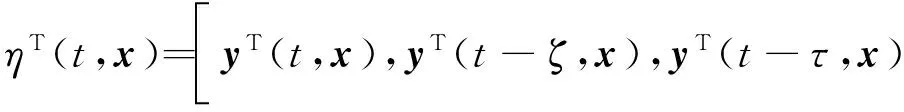






3 数值模拟

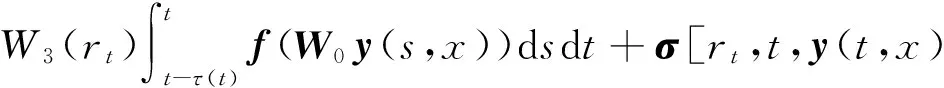


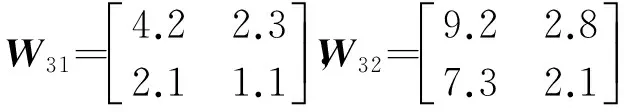


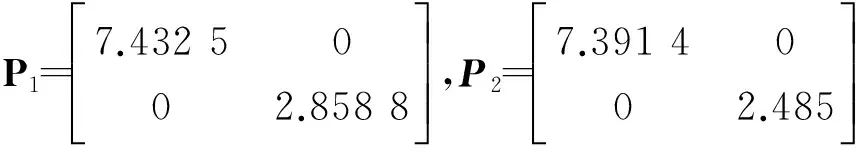


4 结论

