装备对抗目标的随机灰色期望值分配模型
柯宏发,柯肇敏,祝冀鲁
(1.装备学院复杂电子系统仿真重点实验室,北京 102206; 2.中国矿业大学(北京)化学与环境工程学院,北京 100083)
装备对抗目标的随机灰色期望值分配模型
柯宏发1,柯肇敏2,祝冀鲁1
(1.装备学院复杂电子系统仿真重点实验室,北京 102206; 2.中国矿业大学(北京)化学与环境工程学院,北京 100083)
针对装备对抗目标分配问题中的随机、灰色双重不确定性,建立了装备对抗目标的随机灰色期望值分配模型。首先,给出了随机灰色变量的定义,研究了随机灰色变量的加(减)、乘、除、大小关系运算和期望值算法;其次,建立了装备对抗目标的多目标随机灰色期望值模型和标准随机灰色期望值目标规划模型;最后,给出了电子装备侦察地域的随机灰色期望值分配实例,并将其转化为一般灰色线性规划模型进行求解。结果表明:该模型可应对装备对抗目标分配问题中的随机灰色特征,在目标分配领域具有潜在的应用价值。
装备对抗目标; 目标分配模型; 不确定性; 期望值; 随机灰色变量; 灰色线性规划
随着装备的体系化、信息化、网络化发展,战场环境复杂多变,涌现性多,不确定程度高,装备对抗目标分配成为装备体系化、网络化优化配置的关键,也是多武器无缝链接与协同、实现一体化火力打击的有效方式。建立装备对抗目标分配模型可使得有限的武器装备资源实现协同配合、整体优化,从而获得最佳的对敌目标作战效果。装备对抗目标的分配问题涉及分配机制、分配模型和求解算法等[1-2],分配模型与求解算法更是其中的研究热点,其中:KE等[3]提出了贫信息下作战目标的GM(1,1)分配模型;HU等[4]提出了一种编组无人机作战目标的层次式分配模型。
由于武器装备与作战目标的对抗过程中存在大量灰色、随机、模糊等单式不确定性,也存在模糊随机、灰色随机、随机灰色等混合不确定性现象,因此在不确定性环境下研究装备对抗目标分配问题比较符合实际背景,也取得了诸多研究成果[5-8]。如:笔者课题组[5]针对电子装备试验训练过程中存在随机性特征参数的问题,分别建立了电子侦察装备的单目标和多目标随机期望值分配模型,并给出了目标规划方法和遗传算法求解步骤;范成礼等[8]针对反导目标分配优化问题中存在的不确定性特征,引入模糊随机规划理论,建立了基于模糊随机规划的反战术弹道导弹的目标分配优化模型。尽管在武器装备对抗目标分配问题中可采用随机变量[9-10]描述装备的作战能力,但由于对装备作战对象、作战环境等信息很难完全掌握,大部分情况下缺乏大量的统计数据,难以确定作战能力的均值和方差,因此单纯地采用随机变量描述装备的作战能力就会产生较大的局限性,这时可采用需要较少统计数据的灰色变量进行描述。基于此,针对装备对抗目标分配问题中的随机、灰色双重不确定性,笔者利用随机灰色变量来描述随机灰色现象,从而建立装备对抗目标的随机灰色期望值分配模型。
1 随机灰色变量
1.1 随机灰色变量的定义
借鉴随机模糊变量的相关定义[11],笔者认为:随机灰色变量是从灰色变量空间到随机变量空间构成的背景或论域的可测函数,其实质是一个取值为随机变量的灰色变量。
定义1:假设ξ是一个从灰色概率空间(Ω,F,P)到随机变量论域的函数,若函数f(ξ)是灰色概率空间(Ω,F,P)上的可测函数,则称ξ为一个随机灰色变量。
假设某型号电子侦察装备对某频段内信号的侦察概率p服从正态分布,即有p~N(p′,δ2),其中参数p′通常希望通过试验采集样本进行统计估计,但实质上难以采集足够的数据样本,很多情况下给出一个信息不完全情况下的灰数,这时的侦察概率p就是一个取值为正态随机变量的随机灰色变量。
假设参数p′通过n种不同可能性前提下的灰数进行表达,即有
(1)
则p就是一个n维随机灰色变量。式(1)在实际工程应用中等价表达为
(2)
假设ξ是一个灰色概率空间(Ω,F,P)上的随机灰色变量,如果对于每一个φ∈Ω,期望值E[ξ(φ)]是一个从灰色概率空间(Ω,F,P)到区间灰数集的函数,则E[ξ(φ)]是灰色概率空间(Ω,F,P)的一个灰色变量。
定义2:假设η是一个灰色概率空间(Ω,F,P)上的随机灰色变量,u是一个随机变量,v是灰色变量,并且
ξ(ω)=η(ω)+u,∀ω∈Ω,
(3)
如果pos{ξ(ω)∈Ω}是ω在灰色概率空间(Ω,F,P)上的可测函数,则称ξ=η+u为一个随机灰色变量。类似地,假设
ξ(ω)=η(ω)v,∀ω∈Ω,
(4)
如果pos{ξ(ω)∈B}是ω在灰色概率空间(Ω,F,P)上的可测函数,则称ξ=ηv为一个随机灰色变量。
1.2 随机灰色变量的数学运算
假设ξ和η是2个相互独立的、维数分别为n和m的随机灰色变量,其中
随机灰色变量的加(减)、乘、除和大小关系运算如下:
1)加(减)运算
对于随机灰色变量ξ和η的加(减)运算,即求ϑ=ξ±η。由于ξ为n维随机灰色变量,η为m维随机灰色变量,则其和(差)ϑ为mn维随机灰色变量,即
ϑ=ξ±η=
(5)
由式(5)容易看出:随机灰色变量ξ和η的加运算满足交换律,即ξ+η=η+ξ;随机灰色变量ξ、η和χ的加运算满足结合律,即(ξ+η)+χ=ξ+(η+χ)。
2)乘运算
对于随机灰色变量ξ和η的乘运算,即求ϑ=ξη。由于ξ为n维随机灰色变量,η为m维随机灰色变量,且二者相互独立,则其乘积ϑ为mn维随机灰色变量,并有
ϑ=ξη=
(6)
由式(6)容易看出:随机灰色变量ξ和η的乘运算满足交换律,即ξη=ηξ;随机灰色变量ξ、η和χ的乘运算满足结合律,即(ξη)χ=ξ(ηχ)。
3)除运算
同理,对于随机灰色变量ξ和η的除运算ϑ=ξ÷η,ϑ也为mn维随机灰色变量,其表达式类似于式(6),将ξη置换为ξ/η,ξiηj(i=1,2,…,n;j=1,2,…,m)置换为ξi/ηj即可。
4)大小关系
对于随机灰色变量ξ,如果有min(ξ1,ξ2,…,ξn)>0成立,显然有ξ>0;若ξ1=ξ2=…=ξn=0,则有ξ=0;若max(ξ1,ξ2,…,ξn)<0,则有ξ<0。同样,在武器装备对抗目标分配问题中,大多数情况是讨论ξ>0时的随机灰色变量。
对于任意随机灰色变量ξ、η和χ,令ξ=η-χ,若有ξ>0、ξ=0或ξ<0成立,则定义η>χ、η=χ和η<χ。但在实际工程应用中,更多的是min(ξ1,ξ2,…,ξn)<0和max(ξ1,ξ2,…,ξn)>0的情况,从样本概率的角度出发,给出如下定义。
定义3:假设2个随机灰色变量ξ和η,并有
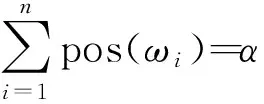
令
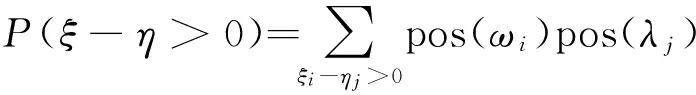
(7)
则有
(1)若P(ξ-η>0)=αβ,则称ξ>η;
(2)若P(ξ-η>0)=0,则称ξ≤η;
(3)若0
1.3 随机灰色变量的期望值
定义4:假设ξ是定义在灰色概率空间(Ω,F,P)上的随机灰色变量,则称
(8)
为随机灰色变量ξ的期望值(为了保证随机灰色变量ξ的期望值有意义,要求式(8)右端2个积分中至少有1个有限)。
定义5:假设ξ是定义在灰色概率空间(Ω,F,P)上的随机灰色变量,并有
则称灰数
(9)
为随机灰色变量ξ的期望值。
对于2个相互独立的随机灰色变量ξ、η,根据定义5,容易证明其期望值有下列性质:
1)E[ξ+η]=E[ξ]+E[η];
2)设a、b为实数,则有E[aξ+b]=aE[ξ]+b;
3)由于ξ、η相互独立,则有E[ξη]=E[ξ]E[η];
4)假设E[ξ]>E[η],则有ξ>η。
定义6:假设ξ是定义在灰色概率空间(Ω,F,P)上的随机灰色变量,且其期望值E[ξ]有限,则称
V(ξ)=E[(ξ-E[ξ])2]
(10)
为随机灰色变量ξ的灰色方差。
根据期望值E[ξ]的定义,有
V(ξ)=E[ξ2]-(E[ξ])2=
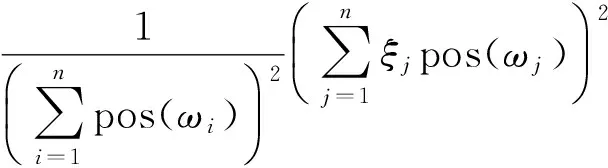
(11)
很显然,由式(11)可证明灰色方差V(ξ)具有下列性质:
1)设a为实数,则有V(aξ)=a2V(ξ);
2)假设ξ、η相互独立,则有V(ξ±η)=V(ξ)±V(η)。
2 随机灰色期望值规划模型
随机灰色规划是在随机灰色环境中的优化理论,可通过随机灰色规划建模解决含有随机灰色信息的优化问题。为了使决策在期望约束下得到最大(或最小)的期望效益,定义随机灰色期望值分配模型的标准形式为
maxE[f(x,ξ)],
(12)
st.E[gk(x,ξ)]≤0,k=1,2,…,K。
(13)
式中:x为一个决策向量;ξ为一个随机灰色向量;f(x,ξ)为目标函数;gk(x,ξ)为随机灰色约束函数。
在装备对抗目标分配问题中,常常涉及到多个期望目标,这时可建立的多目标随机灰色期望值模型为
max(E[f1(x,ξ)],…,E[fL(x,ξ)]),
(14)
st.E[gk(x,ξ)]≤0,k=1,2,…,K。
(15)
式中:fl(x,ξ)(l=1,2,…,L)为目标函数。
为了平衡多个目标的冲突,指挥控制系统可根据各个不相容目标的重要程度对其进行等级划分,并按照这个顺序尽可能满足更多的目标。这种思路是多目标规划的建模思想。基于随机灰色环境下的多目标规划建模思想,建立标准的随机灰色期望值目标规划模型,即
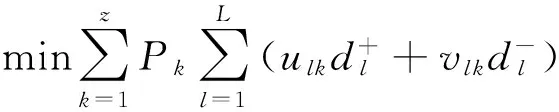
(16)
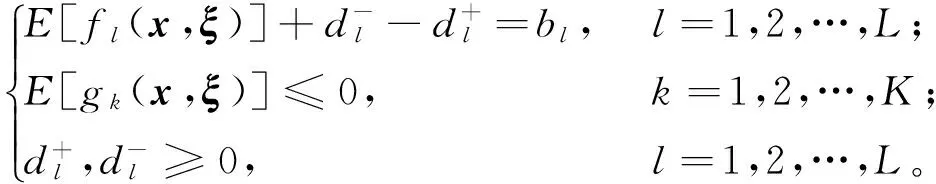
(17)
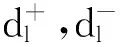
3 电子装备侦察地域的随机灰色期望值分配实例
在电子装备的对抗目标分配问题中,除了对电子装备的对抗目标进行规划外,由于对抗目标的地域差异,通常还需要对其作战地域进行规划。但在实际的目标分配方案设计活动中,电子装备针对具体作战地域的作战能力缺乏具体的描述数据,只能通过以往的少量经验数据进行估计,给出的估计数据大多数情况下符合随机灰色环境。
例如,基于侦察效能进行电子侦察装备的侦察地域分配。该电子侦察系统包括Ⅰ、Ⅱ、Ⅲ型3种类型各8、13、10套,共31套的电子侦察装备需要分配,以对A、B、C、D四个地域内的信号进行侦察,分配关系如图1所示。为了确定电子侦察装备分配使用的最优计划,这里用8个规划变量来表示电子侦察装备的一个分配方案。其中:x11、x12、x13表示Ⅰ型电子侦察装备分配给地域A、B和C的数量;x22、x23、x24表示Ⅱ型电子侦察装备分配给地域B、C、D的数量;x31、x34表示Ⅲ型电子侦察装备分配给地域A、D的数量。

图1 电子侦察装备分配关系
电子侦察装备对作战地域的侦察效能用信号侦察概率来表示,利用随机灰色变量描述3种类型电子侦察装备对A、B、C、D四个地域内信号侦察概率p11、p12、p13、p22、p23、p24、p31、p34,它们分别表示为
为了实现对A、B、C、D四个地域内敌方信号进行最大概率条件下的侦察,需要确定4个地域内信号的侦察概率条件,分别用随机灰色变量ξ1、ξ2、ξ3、ξ4表示。假设其表达式分别为
对电子侦察装备进行分配,以满足对4个地域内信号的侦察需求,规划目标是使电子侦察系统的侦察效能达到最大,可建立的随机灰色期望值模型为
x22E[p22]+x23E[p23]+x24E[p24]+
x31E[p31]+x34E[p34])。

根据随机灰色变量期望值模型,可以得到:E[p11]=0.835,E[p12]=0.8,E[p13]=0.74,E[p22]=0.7,E[p23]=0.815,E[p24]=0.805,E[p31]=0.79,E[p34]=0.78;E[ξ1]=4.9,E[ξ2]=5.3,E[ξ3]=4.6,E[ξ4]=5.2。上述随机灰色期望值模型转化为一般灰色线性规划模型为
0.815x23+0.805x24+0.79x31+0.78x34)。

其解为
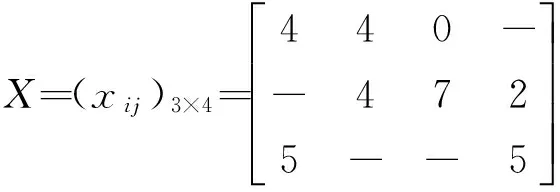
即分配给地域A、B、C的Ⅰ型电子侦察装备数量分别为4、4、0,分配给地域B、C、D的Ⅱ型电子侦察装备数量分别为4、7、2,分配给地域A、D的Ⅲ型电子侦察装备数量分别为5、5。X中“-”表示某类型装备与相应地域之间无作用关系。在这种分配模式下,电子侦察系统对A、B、C、D四个地域内的平均信号侦察概率为0.790 5。
本例若用随机变量直接描述电子侦察装备的信号侦察概率,在使电子侦察系统的侦察效能达到最大目标下,可建立的随机期望值模型为
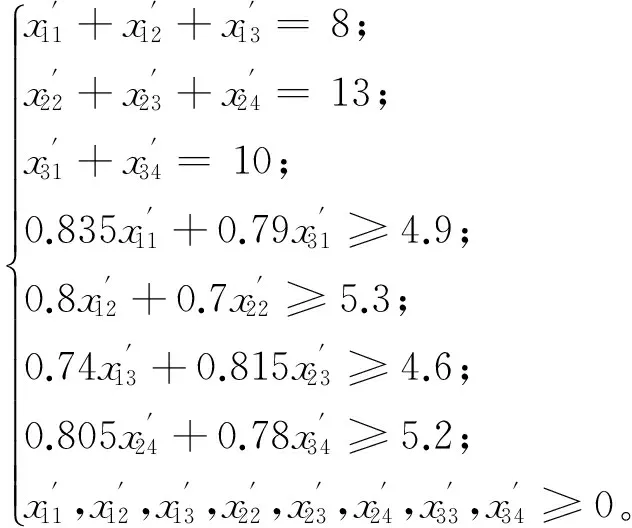
其解为
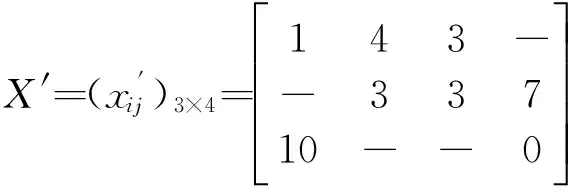
这时,电子侦察系统对A、B、C、D四个地域内的平均信号侦察概率为0.771 8,而采用随机灰色变量时平均信号侦察概率为0.790 5,这种分配模式下电子侦察系统的平均信号侦察概率得到了提高。另外,若以随机变量直接描述4个地域内信号的侦察概率条件时,本例将无最优解。
4 结论
针对装备对抗目标分配问题中随机、灰色双重不确定性特征,建立了装备对抗目标的多目标随机灰色期望值分配模型和多目标情形下标准随机灰色期望值目标规划模型。实例结果证明:随机灰色期望值模型是处理随机灰色现象的有效方法,可有效应对装备对抗目标分配问题中的随机灰色特征。但除了关心期望值的最大化或最小化之外,往往也需要考虑可靠性问题,即决策事件发生的概率(或置信度问题),这时需要建立随机灰色背景下的随机机会约束规划、随机相关机会规划[11]等模型,这是下一步有待深入探讨的问题。
[1] 于连飞,刘进,张维明,等.武器目标分配问题算法研究综述[J].数学的实践与认识,2016,46(2):26-32.
[2] 韦刚,高嘉乐,孙文.多目标多武器系统目标分配模型与算法研究[J].飞航导弹,2016(5):77-82.
[3] KE H F,CHEN Y G,WANG G Y.Target assignment model of electronic equipments based on GM(1,1) model[J].The journal of grey system,2005,17(3):235-242.
[4] HU X X,MA H W,YE Q S,et al.Hierarchical method of task assignment for multiple cooperating UAV teams[J].Journal of systems engineering and electronics,2015,26(5):1000-1009.
[5] 柯宏发,陈永光,戴增刚.电子侦察装备的随机期望值分配模型与算法[J].装甲兵工程学院学报,2013,27(4):60-64.
[6] ZHANG J L.Resource planning and allocation problem under uncertain environment[J].Journal of systems science and complexity,2015,28(5):1115-1127.
[7] GUO J S,WANG Z T,ZHENG M F,et al.Uncertain multi-objective redundancy allocation problem of repairable systems based on artificial bee colony algorithm[J].Chinese journal of aeronautics,2014,27(6):1477-1487.
[8] 范成礼,邢清华,郑明发,等.基于模糊随机规划的反TBM目标分配优化模型[J].系统工程理论与实践,2015,35(9):2401-2409.
[9] 朱昌锋.基于随机灰色蚁群神经网络的集装箱结点站运量预测[J].铁道科学与工程学报,2011,8(2):81-85.
[10] 王庆荣,张秋余.基于随机灰色蚁群神经网络的近期公交客流预测[J].计算机应用研究,2012,29(6):2078-2080.
[11] 刘宝碇,赵瑞清,王纲.不确定规划及应用[M].北京:清华大学出版社,2003.
(责任编辑:尚菲菲)
Equipment Target Assignment Model Based on Random Grey Expected Value
KE Hong-fa1,KE Zhao-min2,ZHU Ji-lu1
(1.Key Laboratory of Complex Electronic System Simulation,Equipment Academy,Beijing 102206,China;2.College of Chemical and Environmental Engineering,China University of Mining & Technology(Beijing),Beijing 100083,China)
According to analysis about complex uncertainty of random grey feature for equipment target assignment,an equipment target assignment model based on random grey expected value is proposed.Firstly,the definition is given,and operational rules including addition,subtraction,multiplication,division,cooperation and expected value,of random grey variables is studied.Secondly,the equipment target model based on multi-objective random grey expected value and the standard objective programming model based on random grey expected value are set up.Finally,an example of assignment model based on random grey expected value for electronic equipment reconnaissance area is given and the model is transformed to general grey linear programming model which is easy to solve.The experimental results indicate that the proposed model can deal with random grey characteristic of equipment target assignment and has potential application value.
equipment target assignment; target assignment model; uncertainty; expected value; random grey variable; grey linear programming
1672-1497(2017)01-0099-06
2016-09-27
军队科研计划项目
柯宏发(1969-),男,教授,博士。
N949; N941.5
A
10.3969/j.issn.1672-1497.2017.01.021

