基于气动反问题的扩压叶栅优化设计

姜俊锋，陈 榴，胡 磊，戴 韧

1 前言

轴流风扇和压气机叶型的基本构造方法是在标准的中弧线上迭加标准厚度分布，例如NACA65系列［1］。这样构造出来的叶栅具有丰富的气动性能试验数据和详细的设计应用准则［2,3］。选择合适的叶栅稠度和叶片安装角，即可满足风扇设计速度三角形的要求。随着叶栅气动优化方法的发展，风扇叶型设计突破了标准叶型的束缚，依据具体工况要求，采用某种优化算法，寻找与某个优化目标的最佳值所对应“定制”叶型，提高了叶型的气动性能。跨音速流动可控扩散叶型和低速流动的自然层流叶型是2个重要成果［4～6］。

叶栅气动优化方法需要大量的流场计算，虽然鲁棒性好，但是耗费的机时令人难以接受［7］。尤其重要的是，优化结果的筛选完全取决于优化算法的能力，往往陷入所谓的“局部”优化，而且得到的优化解往往缺乏合理的物理解释。另一方面，经过长期的气动力学研究，我们已经掌握了具有较好气动性能叶型的流动分布特征。如果能预先给出某个气动目标，再寻找对应的叶型并做优化，那么就可以节省大量的计算费用，而且得到的解也具有物理上的合理性。

与叶栅流动的正问题相比，反问题的理论还不够完善。叶栅气动反问题的第一个困难是如何建立气动目标与叶型几何之间的对应关系，因为没有流动方程是以叶型为因变量，而是以速度或压力分布为自变量而建立的。一个直观可行的方法是从某个相近的初始叶型出发，比较其流动与设计目标的差距，逐步修改叶型逼近设计目标［8～10］。其中 Kasra 采用虚拟速度法［8］，Dulikravich等人采用傅里叶级数［9］，姚征采用涡量修正的叶型修改方法［10］。戴韧将旋成面叶栅气动正命题的微分-积分解法与叶型修正的“喷气模型”结合［11］，获得反问题的解，采用正反问题结合的方法实现了叶片反设计。

叶栅反问题求解的第二个难题是预定气动设计目标的可行性是没有保证的，因此，完全精确的反问题解是不存在的。为了解决这个难题，以各种最优化的方法，逼近气动设计目标，获得某种误差范数的最小值所对应的叶型，即为叶栅反问题的解。Pehlivanoglu等采用遗传算法［12］，Obayashi等采用进化算法［13］，丰镇平基于控制理论，采用伴随梯度算法，都取得了不错的成果［14］。

本文利用边界层积分解的Head方法建立叶型表面压力系数分布与边界层积分厚度的关系［15］，利用遗传算法，获得近似最优的压力系数分布。采用反问题的“弹性模型”求解方法，逼近目标压力系数，并结合试验设计方法优选反问题的目标压力系数分布，从而建立基于反问题的优化设计方法。将此方法应用到具体实例进行验证，获得符合气动设计目标的叶型，改善叶栅流场，降低叶型的损失，提高气动性能。

2 叶栅气动反问题设计方法

叶栅气动反问题设计方法的计算流程如图1所示，其中有3个重要步骤：确定目标压力系数分布、初始叶型的流动分析和叶型的修正。叶栅反问题的气动目标与单机翼气动反问题是不同的，因为叶栅进出口速度三角形限定了叶片绕流环量的大小，所给定的气动目标需要满足这个环量的约束，因此满足气动目标的解是有限的。叶型的修正有多种方法，但是修正后叶型的二阶连续是至关重要的，因为型线曲率的间断点是流动发生阶跃的位置，在扩压流动中，会引起边界层的快速增长甚至是分离。

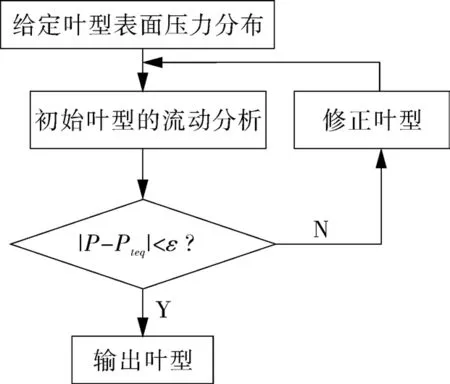
图1 反问题设计流程

2.1 目标压力分布的近似优化

确定一个近似最优的目标压力系数分布是反问题设计中很重要的一步。本文根据Head边界层计算方法，建立边界层外缘速度ue与边界层厚度以及壁面摩擦系数之间的关系。

二维不可压的流体动量积分方程为［15］：

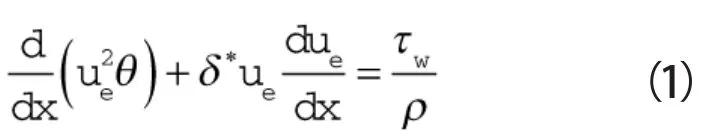
引入Head裹入方程，与式（1）联立求解边界层动量厚度θ沿流向的增长。

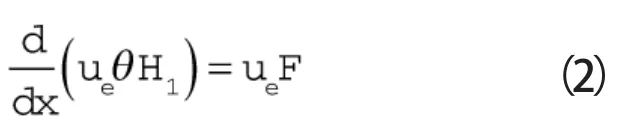
其中 H=δ＊/θ,H1=（δ-δ＊）/θ

式中 H1——形状因子

对于给定的速度分布ue，式（1）、（2）中包含3个未知数θ，Cf和H，还需补充若干关系式才能封闭求解［15］。设想沿叶型表面的速度分布ue（x）表述为由（n+1）点控制的n次参数化多项式：

其中Pi（t）是多项式基函数，ue,i为控制点。利用遗传算法优化{ue,i}，得出一个近似最优的速度分布ue（x）。将此速度分布按照伯努利积分换算得出对应的最优压力系数分布。

选取3种典型的速度分布，如图2所示。经过对比发现，内凹的速度分布具有较小的动量损失厚度，壁面摩擦系数也较小，如图3，4所示。因此以内凹速度分布为初始速度分布进行优化，利用贝济埃（Bezier）曲线对速度分布进行参数化。

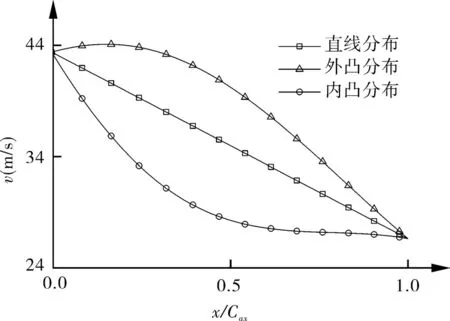
图2 3种典型不同的速度分布

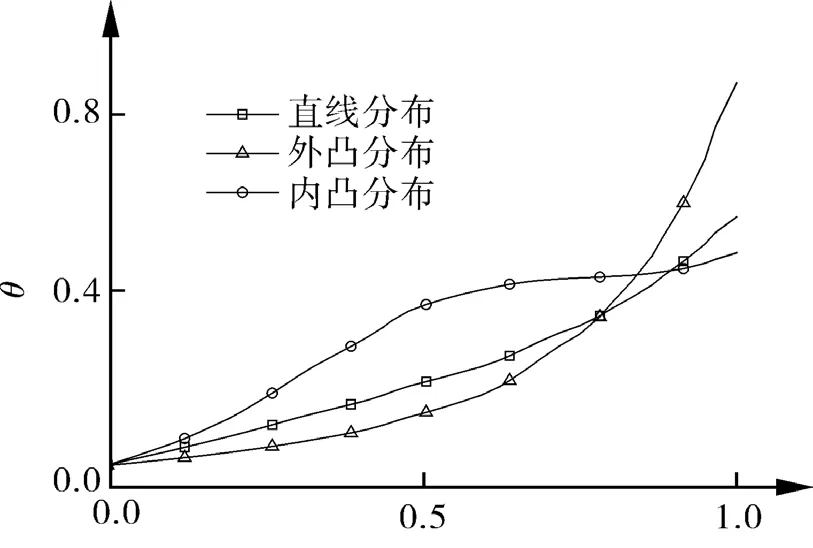
图3 动量损失厚度分布

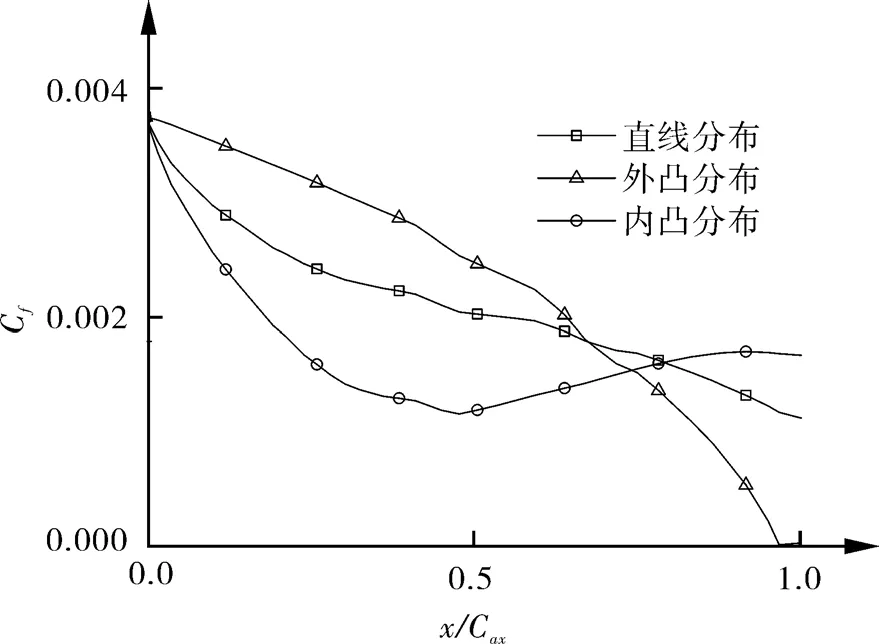
图4 壁面摩擦系数分布

优化目标：

Min：F=θout

Subject to：Cf≤ Cf.baseline

经过优化得到近似最优的速度分布，并按照伯努利方程换算得出对应的压力系数分布如图5所示。最优压力系数分布在x/Cax=0.5之前下降速度较快，曲线的切向与水平面的夹角从15°到55°之间进行变化，x/Cax=0.5之后压力系数变化较小，基本为水平线且带有一定的下凹。

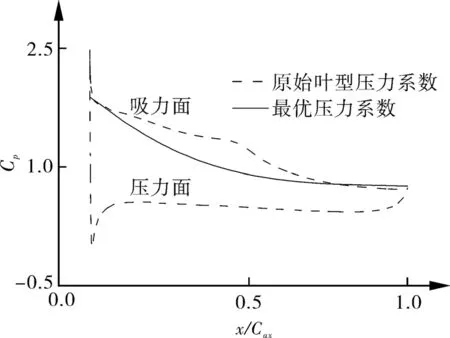
图5 Head方法最优压力系数分布

此压力系数分布是利用Head方法求解出的一个最优的压力系数分布，但是由于Head方法计算的时候没有考虑曲率的影响，以及叶栅流动之间的相互作用等因素，不能直接应用到本文的反问题设计中，还需要结合叶栅流动的特点进行适当的修改。因此以Head求解出的最优压力系数分布为初始压力系数，并利用贝济埃（Bezier）曲线进行参数化，如图6所示，通过控制点使压力系数在最优压力系数附近进行变动，并将此压力系数分布作为目标压力系数分布。控制点仅改变X3，X4和 X5，其余控制点保持不变。

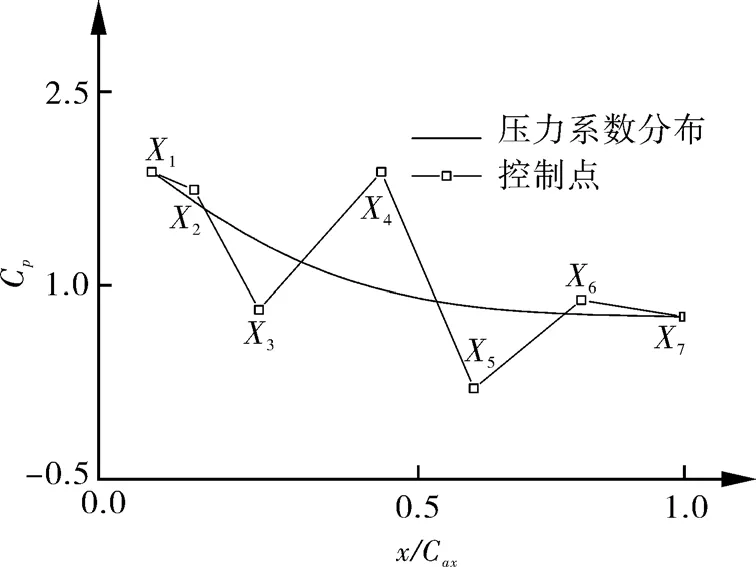
图6 压力系数分布参数化

2.2 叶型气动反问题的解法

叶型气动反问题求解能否成功的关键在于，如何将叶型表面气动参数与气动目标的差距，转换为叶型修改的“动力”。本文将叶片表面视为弹性膜，当初始叶型表面压力与目标值不一致时，在两者之间的压差作用下，叶片表面发生局部“变形”，变形量的大小与当地压差成正比。据此建立叶型修正模型。

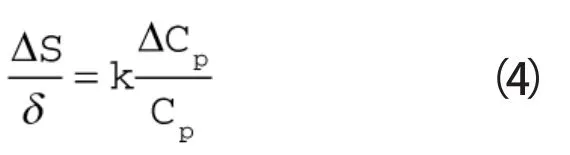
式中 ΔS——叶型表面法向位移

δ——叶型的当地厚度

k——变形率系数，相当与弹性模型。

ΔCp—— 计算压力系数与目标压力系数的差值

Cp——当地压力系数

在叶型表面选取m个反问题目标控制点，覆盖部分叶型，余下叶型自由变动，以满足叶栅总环量的约束。m点叶型的变化后，需要与其余未修正的叶型光滑连接，并保证二阶以上的连续。本文采用附加约束的最小二乘法进行拟合得到新叶型［16］。

采用目标压力的收敛残差Resp和叶型几何残差Resg考核气动反问题的收敛性，两者分别定义为：

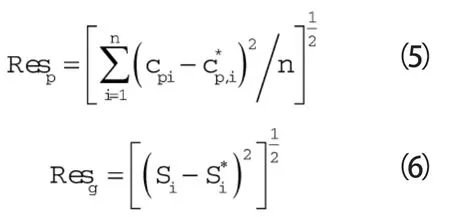
式中 cp——计算压力系数

cp*——目标压力系数

Si——原始叶型控制点

Si*——反设计叶型控制点

2.3 基于反问题的优化设计

应用Head积分，获得叶片吸力面一个最优压力系数分布，作为叶型优化的初始反问题目标，并允许其有一定的“浮动”空间。采用拉丁超立方的试验设计方法，选取n组不同的目标压力系数分布，针对每一组目标压力系数分布进行反问题求解，并对反问题求解出的叶型进行气动性能分析，对比叶栅静压升、总压损失系数以及出口气流角，从而得出较优的反问题叶型。建立以叶型压力分布为自变量的优化问题，称为“气动反问题优化设计”。

3 反问题设计方法的应用

某风扇中截面叶型采用NACA65［17］，叶栅稠度为1.4，叶片安装角16°，进口气流相对叶片弦线的攻角为30度，扩压因子为0.56，超出了最佳气动特性范围［2］。原叶栅流动的CFD分析结果表明，在叶片吸力面的85%弦长位置，流动出现了分离，使得叶型流动损失明显增加，如图7所示。为了提高该风扇的气动性能，采用本文建立的反问题优化设计方法对该叶型进行设计，获得新的气动叶型。

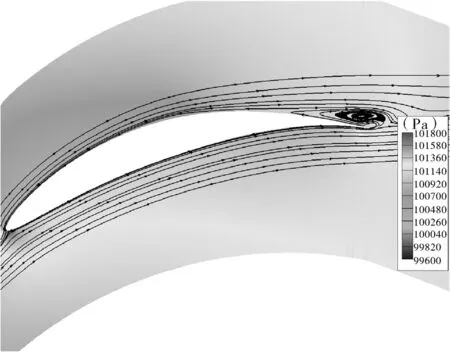
图7 原始叶型速度流线图及压力云图

首先采用拉丁超立方的试验设计方法，给定控制点X3，X4，X5的上下限（0.8，1.2）、（1.6，2.6）、（0.12，0.28），如图6所示，生成20组目标压力系数分布。对每一组目标压力系数分布进行反问题设计，并计算出反设计结果对应的压升δp、总压损失系数cp以及出口气流角β等参数。然后针对这20组样本进行分析，选取较优的压力系数分布作为最终的反问题设计结果。

图8是优化设计过程中，反问题设计叶型的表面压力系数与目标值之间的残差收敛曲线。最终残差稳定在初始残差的7%左右，残差下降了2个数量级。图9是反问题叶型控制点残差的收敛曲线，最终趋于稳定，与压力系数残差趋势一致。由图9可知，第3个控制点的变化较大，其余2个叶型控制点的变化较小。

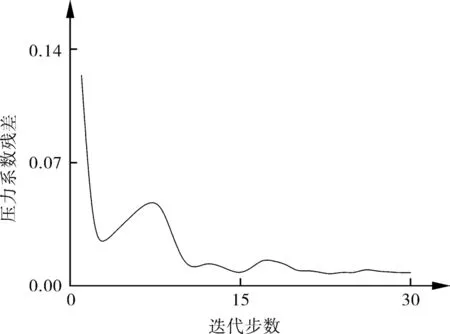
图8 反问题设计压力系数残差变化曲线

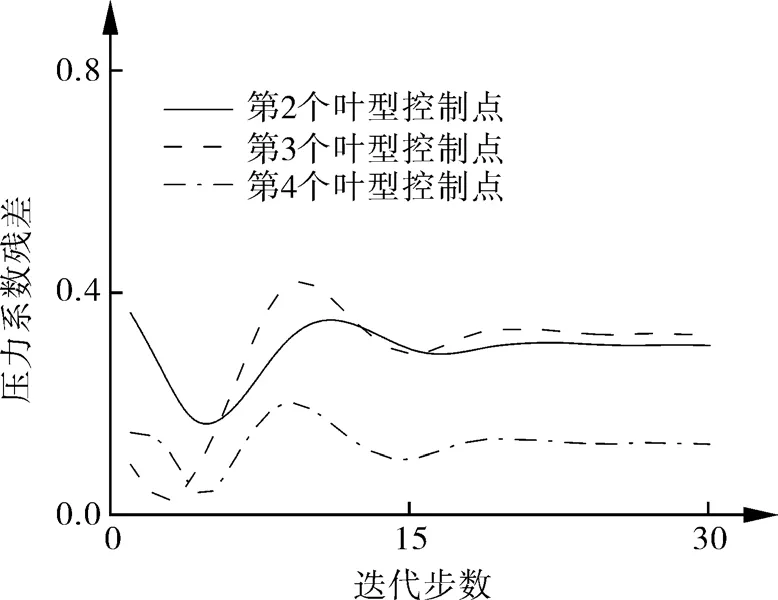
图9 反问题叶型控制点残差变化曲线

目标压力系数分布、计算压力系数分布以及原始压力系数分布，如图10所示，计算的压力系数分布与目标值较为吻合。原始叶型吸力面，在x/Cax=0.4的轴向位置，压力分布有一个“台阶”，在x/Cax=0.85的轴向位置其后流动压力几乎保持不变，也说明x/Cax=0.85以后，吸力面流动是分离的。目标压力系数分布表明，x/Cax=0到x/Cax=0.15的吸力面压力系数提高，x/Cax=0.15到x/Cax=0.7之间压力系数减小。对比反设计叶型与原始叶型发现，x/Cax=0.2到x/Cax=0.8部分的叶型厚度较原始叶型有所减薄，如图11所示。

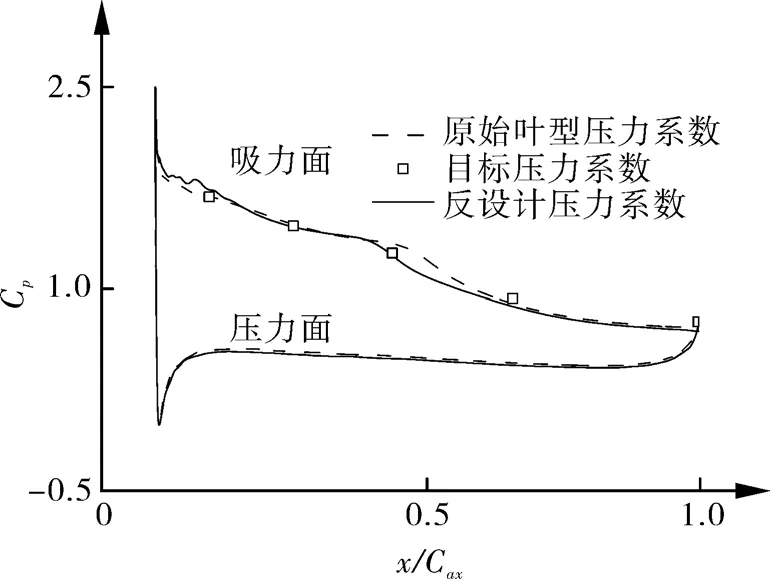
图10 原始叶型与反设计叶型压力系数对比

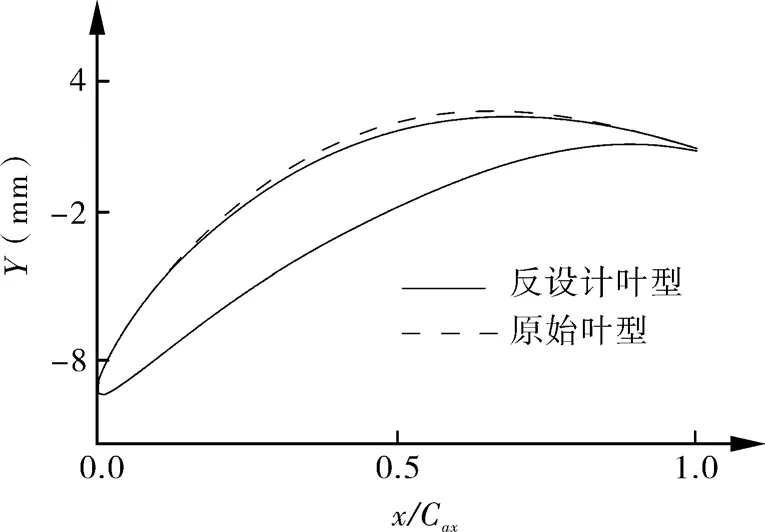
图11 原始叶型与反设计叶型对比

4 反问题设计的验证

本文采用CFX14.0软件，对反问题设计结果进行数值验证。其中湍流模型选择带 γ-θ 转捩的SST模型，计算域采用结构化网格，叶片周围采用O型网格，壁面的Y+≈1，所有网格单元的最小内角正交性都在36°以上，拉伸比＜1000。

图12为叶型优化后，叶栅内流动的速度流线及压力云图。叶栅内分离区较原始叶型有所缩小，叶片尾迹宽度减小。

图12 反设计叶型速度流线及压力云图

图13 为反设计叶型与原始叶型吸力面的曲率对比，由图可知在x/Cax=0.2到x/Cax=0.78之间，反设计叶型要比原始叶型的曲率小，而在x/Cax=0.178到尾缘处则相反。由于叶型曲率的改变，从而改善了整个流场的流动，提高了叶型的性能。曲率分布对流动形态的作用，还有待后续研究。

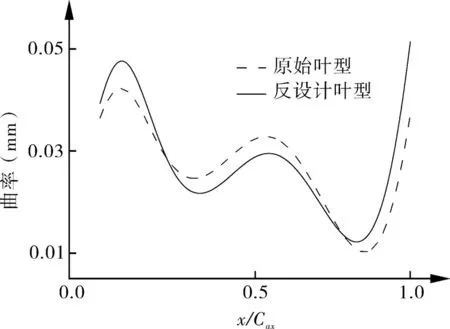
图13 反设计与原始叶型的吸力面曲率对比

表1对比了反设计后叶型阻力系数、升力系数、升阻比以及总压损失系数等参数。新的叶型阻力系数减少16.4%了，升力系数几乎不变，总压损失系数减小了15.6%，总的性能有了较大的提升，证明了本文反问题设计方法是可行的。

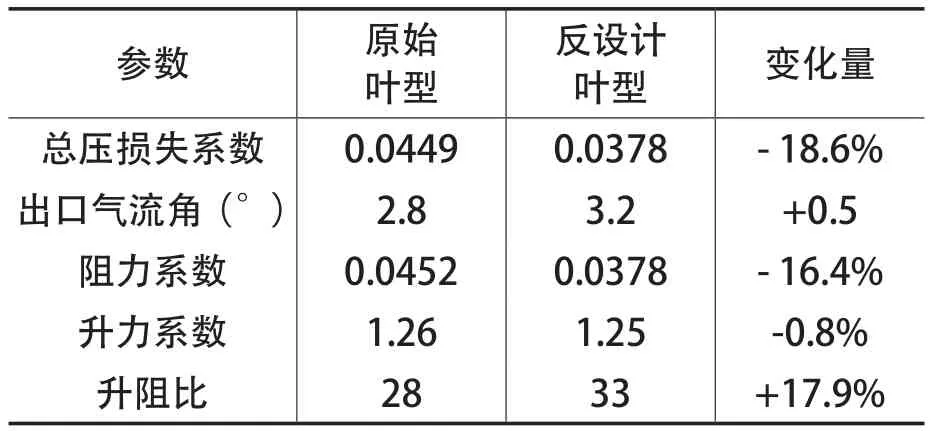
表1 原始叶型与反设计叶型性能参数对比

5 结论

（1） 本文采用的Head边界层厚度计算方法，结合优化算法求解最优的压力系数分布的方法具有可行性。成功地将边界层厚度的计算应用到叶型的反设计中，并结合优化算法求解出近似最优的压力系数分布。

（2） 叶型的修改是反问题的核心，本文采用的“弹性模型”修改叶型的方法，成功的设计出了满足要求的叶型，表明本文的叶型修改方法是成功的。同时表明本文建立的反问题求解程序不仅具有求解速度快，而且具有较好的实用性以及可靠性。

［1］ 王仲奇，秦仁，透平机械原理［M］. 北京：机械工业出版社，1988.

［2］ Herrig L J，Emery J C，Erwin J R. Systematic twodimensional cascade tests of NACA 65-Series compressor blades at low speeds［R］. NACA TN3916 Report Archive & Image Library，1951.

［3］ 轴流压气机气动设计［M］. 北京：国防工业出版社，1975.

［4］ Hobbs D E，Weingold H D. Development of controlled diffusion airfoils for multistage compressor application［J］. Journal of Engineering for Gas Turbines and Power，1984，106（2）：271-278.

［5］ Somers D M. Design and experimental results for a natural-laminar-flow airfoil for general aviation applications［R］. NASA Technocal Paper 1865，1981.

［6］ Gopalarathnam A，Selig M S. Low-speed naturallaminar-flow airfoils：Case study in inverse airfoil design［J］. Journal of aircraft，2001，38（1）：57-63.

［7］ Shahpar S. A Comparative Study of Optimisation Methods for Aerodynamic Design of Turbomachinery Blades［C］. ASME 2000-GT-523 - ASME Turbo Expo 2000：Power for Land，Sea，and Air. 2000：V001T03A087-V001T03A087.

［8］ Kasra Daneshkhah，Wahid S. Ghaly. An inverse blade design method for subsonic and transonic viscous flow in compressors and turbines［J］. Inverse Problems in Science & Engineering，2006，14（3）：211-231.

［9］ Dulikravich G S，Dennis B H. Inverse design and optimization using CFD［C］.European Congress on Computational Methods in Applied Sciences and Engineering，ECCOMAS，2000.

［10］ 姚征. 基于涡量修正的叶栅气动优化设计［J］. 空气动力学学报，2001，19（4）：376-382.

［11］ 戴韧，刘高联. 旋成面叶栅气动反命题的新解法（Ⅱ）［J］. 航空动力学报，1994（1）：4.

［12］ Pehlivanoglu Y V，Hacioglu A. Inverse design of 2-D airfoil via vibrational genetic algorithm［J］. Journal of Aeronautics and Space Technologies，2006，2（4）：7-14.

［13］ Obayashi S，Takanashi S. Genetic optimization of target pressure distributions for inverse design methods［J］.AIAA Journal，1996，34（5）：881-886.

［14］ 丰镇平，厉海涛，宋立明，等. 基于控制理论的透平叶栅气动反设计优化［J］. 中国科学：技术科学，2013（3）：257-273.

［15］ Cebeci T，Bradshaw P. Momentum transfer in boundary layers［M］. Washington，DC，Hemisphere Publishing Corp.；New York，McGraw-Hill Book Co.，1977.

［16］ 同济大学计算数学教研室. 数值分析基础［M］.上海：同济大学出版社，1998.

［17］ 陈榴，刘雪骄，戴韧.弯曲动叶对高负荷风扇气动性能的影响［C］. 中国工程热物理学会-流体机械.2013.