连续刚构桥偏载系数合理取值

邬晓光, 刘 英, 贺 攀, 李艺林(长安大学 陕西省桥梁与隧道重点实验室, 陕西 西安 710064)

连续刚构桥偏载系数合理取值

邬晓光, 刘 英, 贺 攀, 李艺林
(长安大学 陕西省桥梁与隧道重点实验室, 陕西 西安 710064)

依托8座载荷试验桥梁,针对连续刚构桥偏载系数的合理取值问题,通过有限元计算值与试验实测值对比,分析了偏载系数的全桥分布规律,确定出连续刚构桥宽跨比和高跨比为偏载系数的主要控制因素,提出了偏载系数计算公式,并将有限元解和公式计算值进行对比,验证了公式精度在±5%范围内.

连续刚构桥; 载荷试验; 宽跨比; 高跨比; 偏载系数

连续刚构桥一般采用变截面单箱单室或单箱多室混凝土箱梁,由于箱梁截面是一个整体,不能像装配式空心板、T梁、小箱梁简单地根据横向分布影响线分配载荷[1].在偏心载荷作用下,箱梁的空间受力比较复杂,实际工程设计中,通常引入偏载系数对平面杆系计算值进行修正,以考虑箱梁的偏载效应.偏载系数可以定义为梁体某个位置在偏载作用下得到梁体的最大效应与对应的横向各个位置效应的平均值之比[2-3],其计算方法有经验系数法、偏心压力法、修正的偏心压力法等.现有研究大多集中于对比分析几种常用计算方法的精度,且均为理论分析[3-7],少有结合现场试验的对比分析,缺乏实例验证;文献[8]在常规跨度布置及截面尺寸情况下,分析得到了连续梁桥偏载系数建议值及其分布规律,但仅仅局限于特定的桥梁,通用性和可操作性有限;文献[9-11]研究了桥梁宽跨比对偏载系数的敏感程度,但仅分析了等截面等跨度连续箱梁偏载系数,对于变截面不等跨连续箱梁尚未探讨.

综上所述,现阶段偏载系数的研究大多局限于连续梁桥,缺乏对连续刚构桥的探讨,且尚未明确偏载系数的主要影响因素及其相关关系,没有提出切实可行的取值建议,理论研究和实践应用均存在一定程度的不足.基于此,本文依托8座载荷试验连续刚构桥,计算值与实测值对比分析偏载系数的全桥分布规律,确定偏载系数的主要影响因素并分析其数学相关关系,提出基于宽跨比和高跨比的偏载系数计算公式,并用2座连续刚构桥的实体模型计算值验证公式正确性,以供工程设计参考.

1 载荷试验

1.1 依托工程

选取10座单箱单室连续刚构桥作为研究对象,其中前8座桥为拟合样本,后2座桥为公式验证桥梁,其基本情况如表1所示.

1.2 静载试验

因试验桥梁众多,本文以小金河大桥为例说明载荷试验操作事项.

经模型分析确定该桥控制截面为边跨0.33 L、6号墩支点、6号墩底、中跨跨中截面, 4个偏载工况. 计算各工况下控制截面内力影响线, 根据影响线分析结果分级加载. 本次试验共需要16辆总重各为350 kN的三轴载重汽车. 各加载工况、载荷效率如表2所示, 满足规范[12]要求.

各测试截面挠度和应变测点布置如图1所示,其中应变数据采用TDS-303静态数据采集仪进行采集,挠度数据采用精密水准仪进行测试,并记录数据.

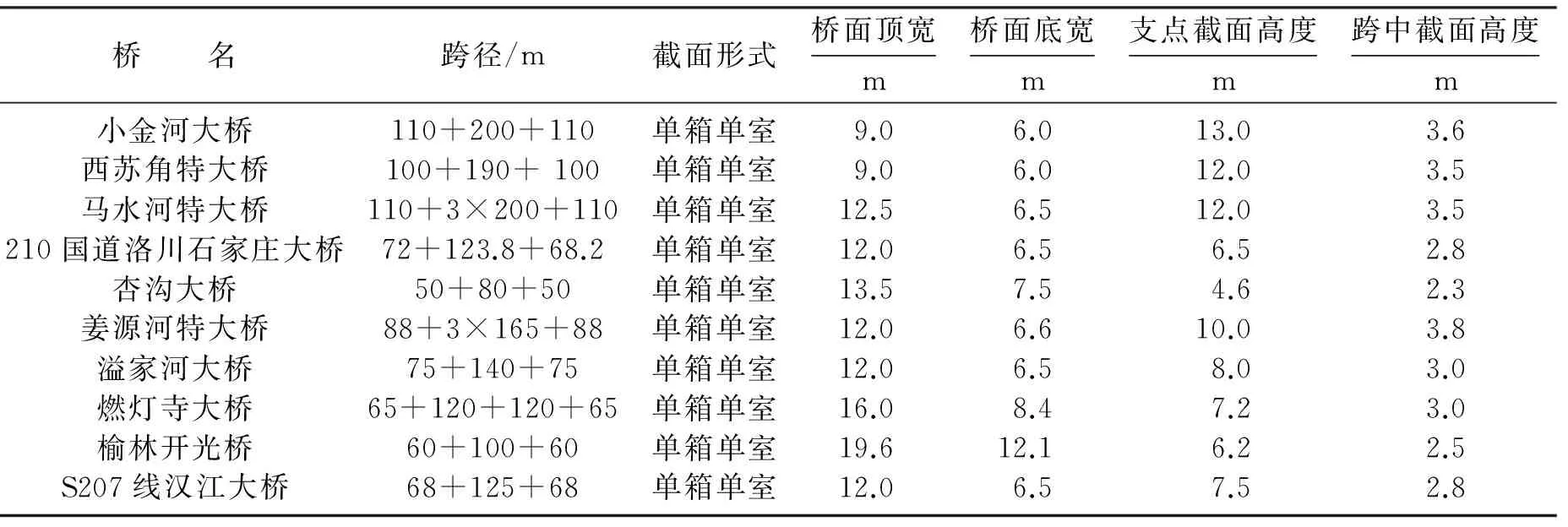
表1 依托连续刚构桥梁概况Table 1 General situation of continuous rigid frame bridges

表2 偏载试验效率表Table 2 The efficiency of the partial load test

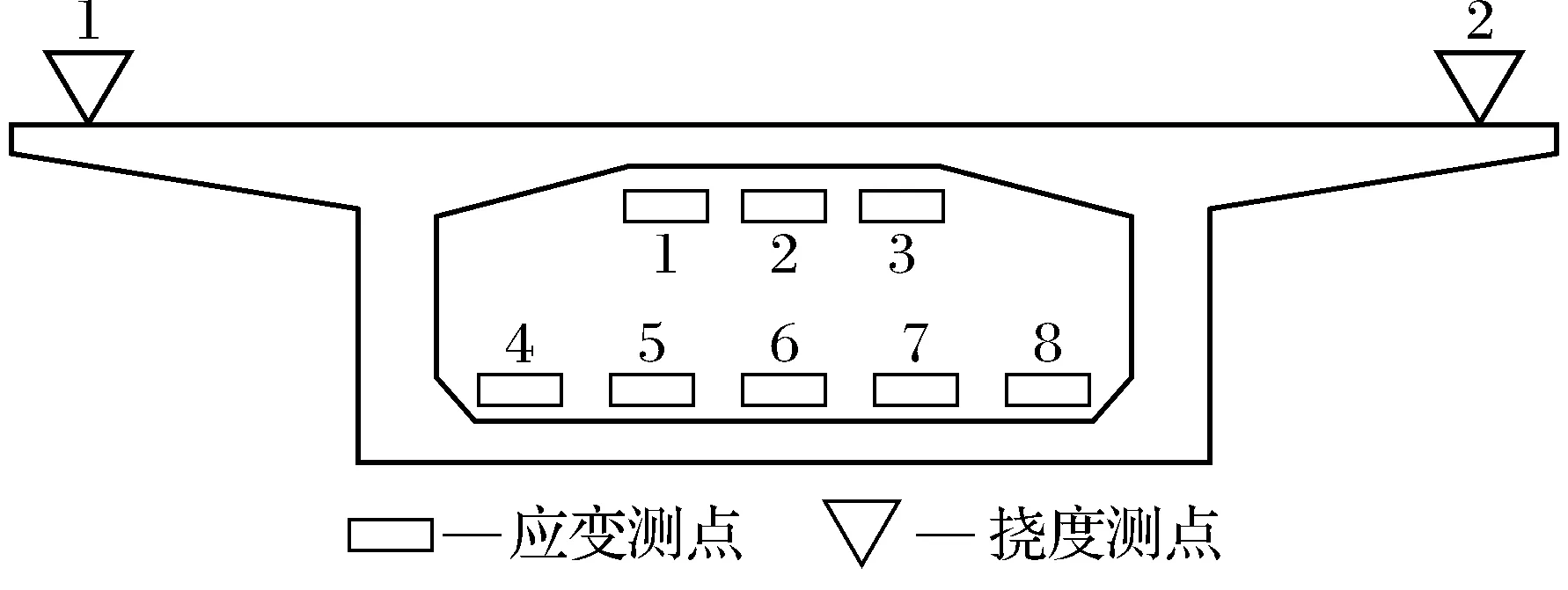
图1 静载试验测点布置图Fig.1 Test point arrangement of static load test

1.3 试验结果

通过静载试验得到小金河大桥各控制断面偏载作用下的应变和挠度值见表3、表4.

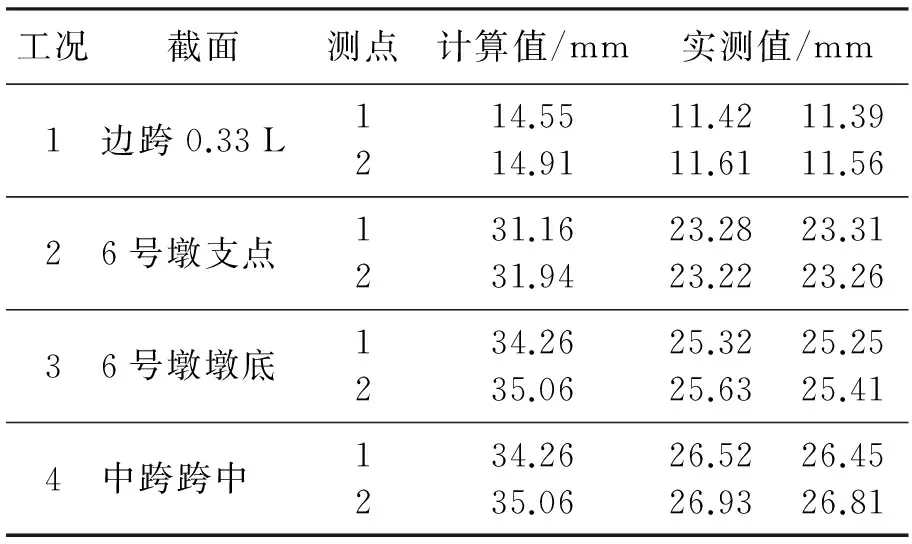
表3 挠度计算值与实测值Table 3 Calculating values and measured data of deflection

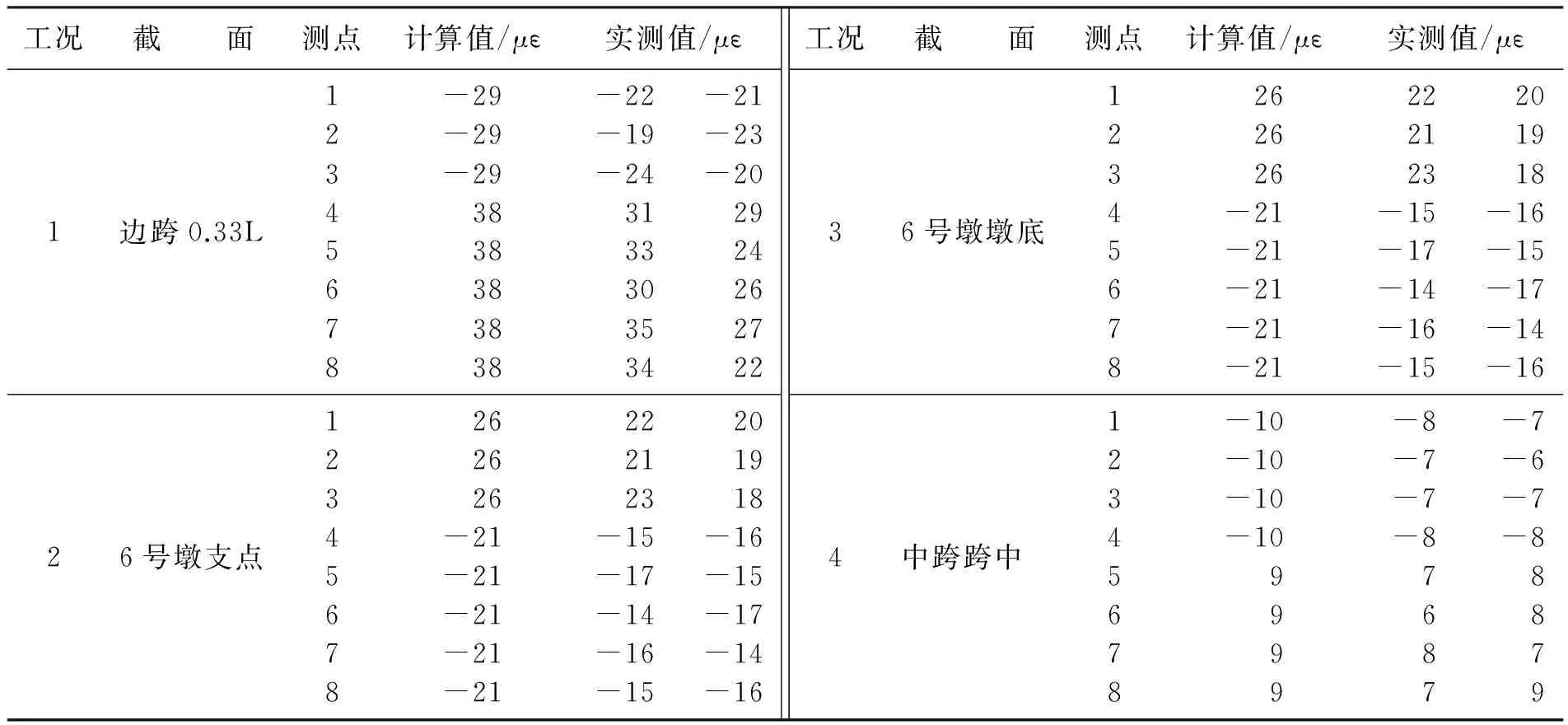
表4 应变计算值与实测值Table 4 Calculating values and measured data of strain

由表3、表4计算挠度校验系数及应变校验系数均满足规范规定,结构刚度、强度均满足设计要求且具有一定的安全储备.

2 连续刚构桥偏载系数研究

基于静载试验结果,用连续刚构桥控制截面位置处最大值效应(挠度和应力)与对应横向各个效应平均值之比表示偏载系数,如表5所示(因分析对象较多,仅列出部分以示说明).

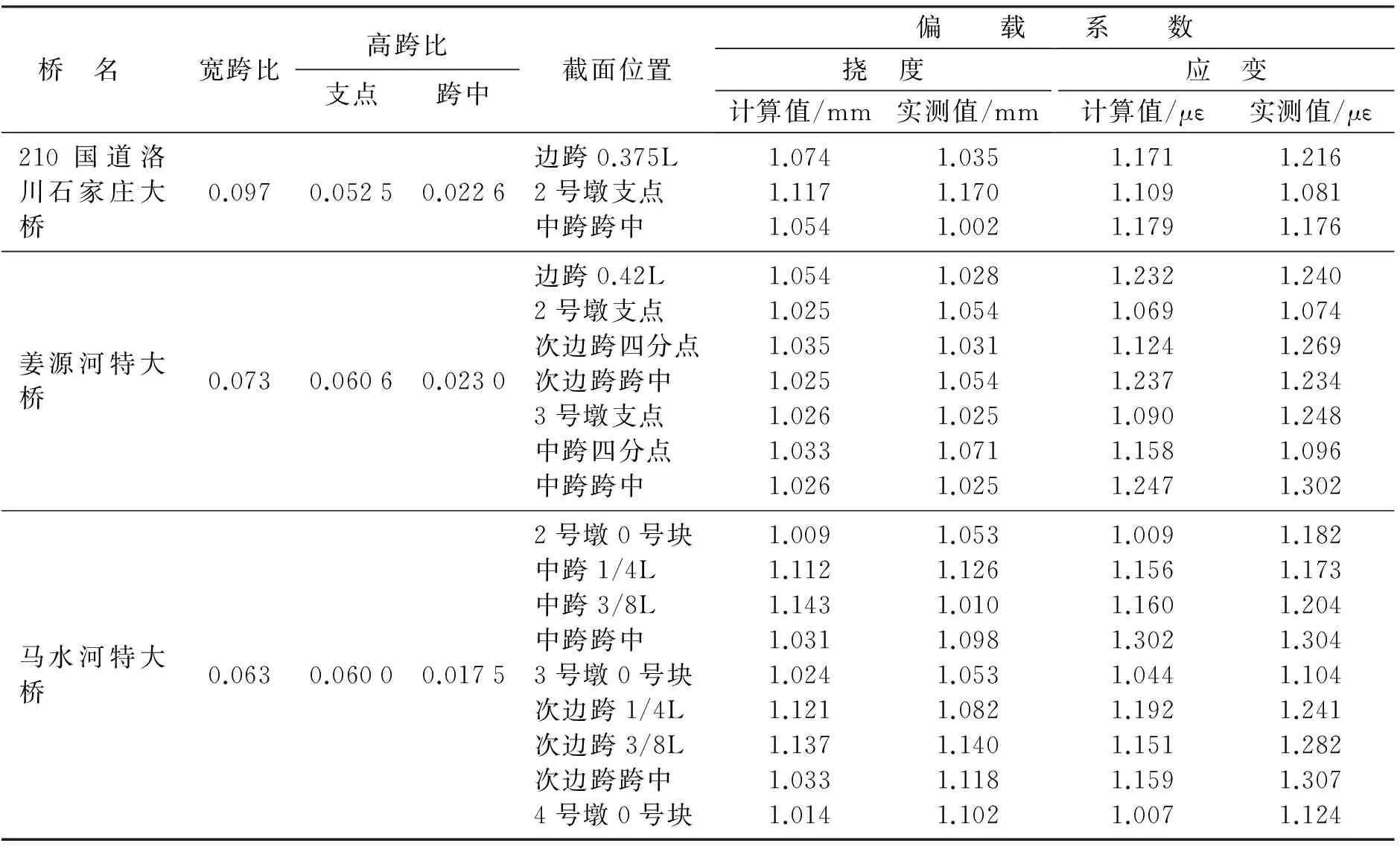
表5 12 m桥宽试验桥梁偏载系数表Table 5 Eccentric load coefficient of 12 m width test bridges

由表5分析可知偏载系数沿全桥的分布是变化的,桥梁跨数较少时,边跨(次边跨)0.4L附近出现最大值,中跨跨中次之,桥墩支点位置处最小;同一座桥边跨偏载系数大于中跨相同位置的偏载系数,表明偏载系数与宽跨比有关;同一跨内L/4截面处偏载系数最大,跨中次之,桥墩支点位置处最小;对于宽跨比相近,高跨比不同的桥梁,相同位置处偏载系数相差很大,表明偏载系数与高跨比存在很大的相关性;按挠度计算的偏载系数实测值与计算值相差无几,且均小于1.15实测值普遍大于计算值,故从挠度角度考虑设计取1.15是安全的;按应变(应力)计算的偏载系数实测值普遍大于计算值,且相差较大,只有少数值小于1.15,故从应力角度考虑,设计取1.15存在安全隐患,故应按应力偏载系数控制设计.

3 连续刚构桥偏载系数公式拟合及验证

以上分析可知宽跨比和高跨比为连续刚构桥偏载系数的主要影响因素.理论上连续刚构的设计应按偏载系数分布规律取值,即不同截面位置处取用不同值,但实际应用时可操作性较差,且不利于提高工作效率,故借鉴经验法的思想宜对全桥采用统一的偏载系数值,取最大值控制设计.各桥梁应力偏载系数最大值如表6所示.

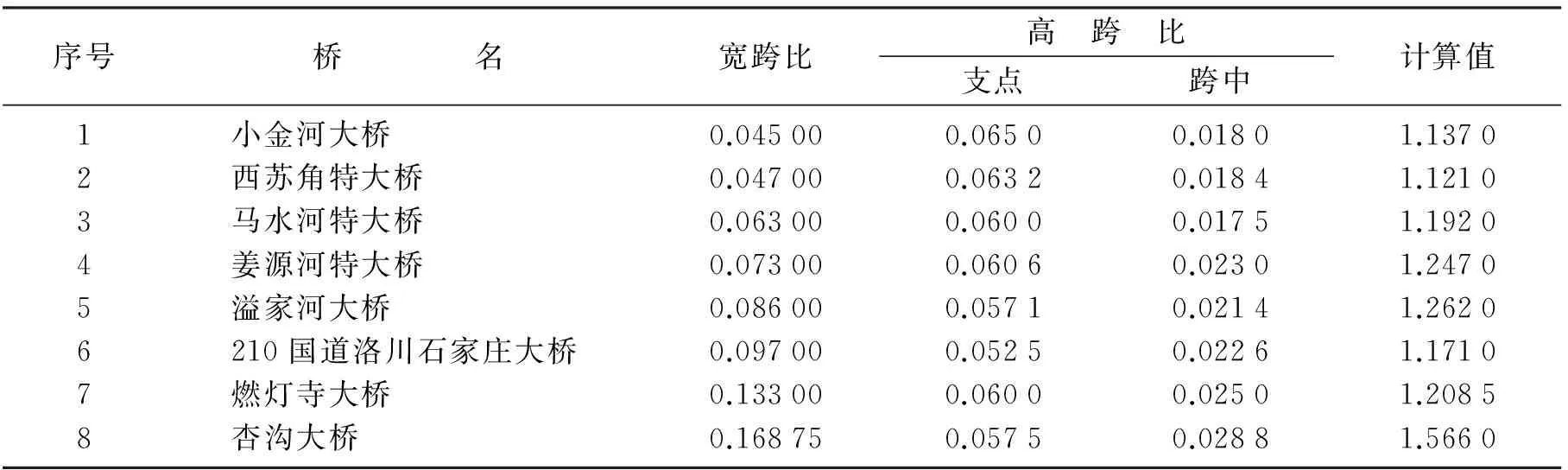
表6 试验桥梁应力偏载系数最大值Table 6 The maximum eccentric load coefficient of test bridges

注:因应变实测值受环境,气候等条件影响较大,故取计算值研究.

用MATLAB拟合偏载系数与宽跨比、高跨比的三维空间关系,公式如下:

其中:ξ支、ξ中、ξ设计分别为按支点高跨比计算、按跨中高跨比计算及设计取用的偏载系数;B为桥梁宽度;L为桥梁标准跨径;H支为墩顶梁高;H中为跨中梁高.

限于试验桥梁均采用单箱单室截面,故此公式仅适用于单箱单室截面连续刚构桥梁的设计,对于其他截面形式还需进一步探讨.

为验证偏载系数计算公式的正确性,选取榆林开关桥和S207线汉江大桥建立Midas FEA实体模型,计算各控制截面的应力偏载系数值,将公式计算值与有限元值对比分析如表7所示.

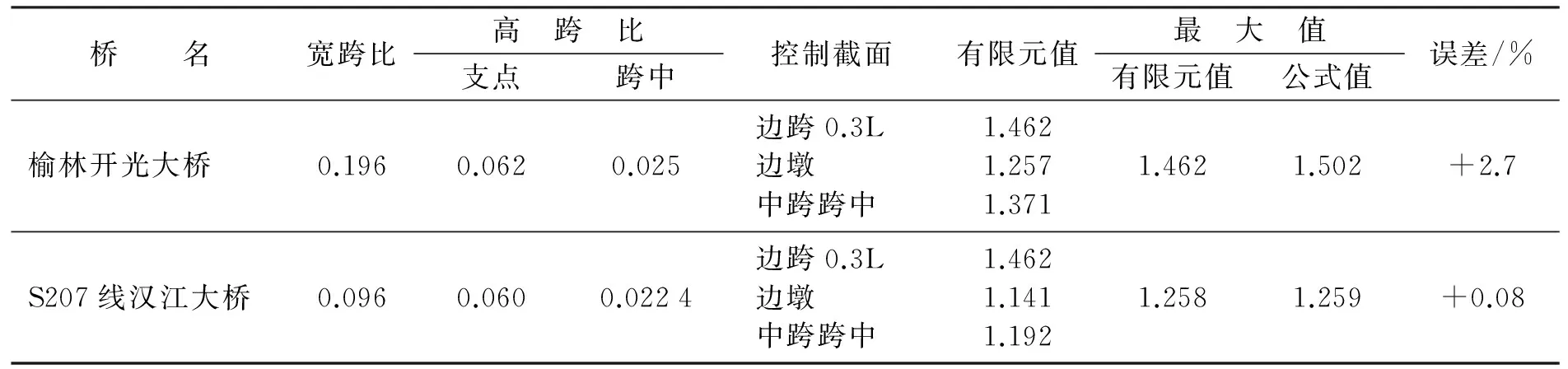
表7 偏载系数公式计算值与有限元计算值对比分析Table 7 Comparative analysis of formula calculating values and finite element solutions of eccentric load coefficient

注:误差=(公式值-有限元值)/有限元值.

偏载系数模型计算值与拟合公式计算值偏差在±5%范围内,满足工程精度要求.

4 结论及建议

(1) 偏载系数沿全桥的分布是变化的,桥梁跨数较少时,边跨(次边跨)0.4L附近出现最大值,中跨跨中次之,桥墩位置处最小.

(2) 同一跨内L/4截面处偏载系数最大,跨中次之,桥墩位置处最小.

(3) 从挠度角度考虑,偏载系数取1.15是安全的,但从应力角度考虑,设计取1.15存在安全隐患,应按应力偏载系数控制设计.

(4) 偏载系数受宽跨比和高跨比的影响较大,基于此提出偏载系数计算式(1)、式(2),实际设计时偏载系数取两公式计算值的平均值即式(3).

(5) 本文提出的偏载系数计算公式初步满足工程精度的要求,单箱单室或其他截面连续刚构桥的设计可适当参考取值同时建立空间模型进一步计算确定,以减少验算次数,保证桥梁结构安全.

[1] 许羿,黄旭. 简支箱梁桥偏载系数的平而杆系有限元计算方法[J]. 重庆交通大学学报, 2008,27(5):672-675. (XU Y,HUANG X. Calculating method of eccentric loaded coefficients of simple supported girder bridges with plane finite bar elements[J].Journal of Chongqing Jiaotong University, 2008,27(5):672-675.)

[2] 徐海军,冷金荣. 城市高架桥异形宽箱梁空间结构分析[J]. 结构工程师, 2010,26 (2):70-75. (XU H J,LENG J R. Three-dimensional analysis of wide irregular box-girders for city viaduct[J]. Structural Engineers, 2010,26 (2):70-75.)

[3] 陈国强. 连续宽箱梁的偏载增大系数的讨论[J]. 公路交通科技, 2013,30(7):66-71. (CHEN G Q. Discussion on eccentric load enhancement coefficient of continuous wide box girder[J]. Journal of Highway and Transportation Research and Development, 2013,30(7):66-71.)

[4] 郭忆,叶见曙,万红燕. 预应力混凝土箱梁偏载系数试验研究[J]. 黑龙江工程学院学报, 2002,16(4):14-16. (GUO Y,YE J S, WAN H Y. Research on pre-stressed concrete box-beam eccentric-loaded coefficients trials[J]. Journal of Heilongjiang Institute of Technology, 2002,16(4):14-16.)

[5] 王勇,刘永健,唐小方. 混凝土连续箱梁偏载系数简化算法研究[J]. 长沙交通学院学报, 2006,22(3):35-39. (WANG Y,LIU Y J,TANG X F. Study on the simplified calculations of the eccentric-loaded coefficients of the continuous concrete box-bean[J]. Journal of Changsha Communications University, 2006,22(3):35-39.)

[6] 陈爱萍,刁荣亭,赵国. 预应力混凝土变宽箱梁偏载系数研究[J]. 山东交通学院学报, 2008,16(3):50-55. (CHEN A P,DIAO R T,ZHAO G. Research on eccentric-loaded coefficients of pre-stressed concrete non-uniform width box-beam[J]. Journal of Shandong Jiaotong University, 2008,16(3):50-55.)

[7] 陆军,张道光. 预应力混凝土变截面连续箱梁桥偏载系数研究[J]. 现代交通技术, 2011,8(3):23-25. (LU J,ZHANG D G. Research on eccentric loaded coefficients of variable cross-section continuous prestressed concrete box girder bridge[J]. Modern Transportation Technology, 2011,8(3):23-25.)

[8] 苏俭,刘钊,阮静. 连续梁桥的活载正应力偏载系数研究[J]. 世界桥梁, 2009(4):34-37. (SU J,LIU Z,RUAN J. Study of eccentric load coefficient of live load normal stress of continuous beam bridge[J]. The World Bridge Journal, 2009(4):34-37.)

[9] MA L,ZHOU L Y,LI S Q,et al. Eccentric load coefficient of live load normal stress of continuous composite box-girder bridge with corrugated steel webs[J]. Procedia Earth and Planetary Science, 2012,5:335-340.

[10] 陈水生,苗守举,桂水荣,等. 单箱多室波形钢腹板箱梁偏载系数参数分析[J]. 工业建筑, 2016,46(5):160-165. (CHEN S S,MIAO S J, GUI S R, et al. Parameter study of eccentric load coefficient of multi-cell single-box composite box girder with corrugated steel webs[J]. Industrial Construction, 2016,46(5):160-165.)

[11] 安丽勇. 桥梁宽度和跨度对城市桥梁活载偏载系数影响的研究[J]. 城市道桥与防洪, 2012(10):49-51. (AN L Y. Study on influence of bridge width and span on urban bridge eccentric coefficient of live load[J]. Urban Roads Bridges & Flood Control, 2012(10):49-51.)

[12] 中华人民共和国交通运输部. 公路桥梁承载能力检测评定规程:JTG/T J21—2011[S]. 北京:人民交通出版社, 2011. (Ministry of Transportation of the People, Republic of China. Specification for inspection and evaluation of load-bearing capacity of highway bridges: JTG/T J21—2011 [S]. Beijing: China Communications Press, 2011.)

【责任编辑: 肖景魁】

Reasonable Value of Eccentric Load Coefficient of Continuous Rigid Frame Bridge

WuXiaoguang,LiuYing,HePan,LiYilin

(Laboratory for Bridge and Tunnel, Chang’an University, Xi’an 710064, China)

For the proper values of eccentric load coefficient of continuous rigid frame bridge, relying on the eight loading test bridges, the eccentric load coefficient distribution regularity of the whole bridge is analyzed by comparing the finite element calculated values with experimental measured values. It is determined that width-span ratio and high-span ratio of continuous rigid frame bridge can be the main control factors of eccentric load coefficient. A calculation formula for eccentric load coefficient is put forward, and the finite element solutions are compared with the formula calculating values to verify that the accuracy of formula is within ±5%.

continuous rigid frame bridge; load test; width-span ratio; high-span ratio; eccentric load coefficient

2016-10-21

陕西省交通运输厅科技资助项目(13-25k).

邬晓光(1961-),男,湖北英山人,长安大学教授,博士生导师.

2095-5456(2017)01-0049-05

U 448.23

A