基于曲率的在线签名认证研究
谭 华,何 朗,黄樟灿,方炫苏,王飞阳
(武汉理工大学 理学院,湖北 武汉 430070)
基于曲率的在线签名认证研究
谭 华,何 朗,黄樟灿,方炫苏,王飞阳
(武汉理工大学 理学院,湖北 武汉 430070)
为了提高签名认证的准确率,提出了一种新的特征提取和距离测度方法。首先对签名曲线进行预处理,其次计算出极值点的曲率值,最后基于离散Fréchet距进行签名认证算法设计,与其他距离测度相比较,离散Fréchet距离明确了两个点集间的点点对应关系,提高了曲线相似判断的精度。实验表明,该算法具有较小的时间复杂度,具有较低的误纳率和误拒率。
签名认证;极值点;曲率;离散Fréchet距;曲线相似
近年来,由于互联网技术的快速发展,如何准确有效地鉴别一个人的身份显得尤为重要,而签名作为一种行为特征,在商务、司法、金融、保险等领域是一种重要的鉴别手段[1-2]。手写签名的研究最早由MANCERI发表了“利用签名进行个人识别的可行性研究”报告,提出了手写签名作为个人身份识别标志的可能性。后来,研究者观察到签名动态特征的重要性,国内许多学者也对手写汉字签名认证进行了探讨和研究,金涌等[3]研究了基于空间曲线弹性匹配的在线手写签名认证;郑建彬等[4]提出了一种基于演化计算的签名认证算法。目前许多研究者对曲线的相似判断产生了兴趣,ZHU等[5-6]利用曲率和挠率算出全曲率,并由全曲率值选出曲线的特征点来进行曲线的匹配复原;LIU等[7]提出利用特征段曲率的Hausdorff距离进行匹配;ZHOU等[8]利用角点及各角点之间的曲线段曲率进行不规则曲线的匹配。随着计算机技术的发展,HOLM等[9]将连续Fréchet距离应用到蛋白质结构排列的相似性上;EFRAT等[10]将曲线的相似性判断应用到了签名认证中;曲线相似性判断是时间序列分析、形状匹配、模式识别和蛋白质结构预测中的一个中心问题,而在线签名认证在模式识别、人工智能、信息传感与中文信息处理领域有着深远的理论研究价值,对于身份认证的技术更新也有一定的现实指导意义[11]。
1 相关工作
1.1数据采集
数据库的建立由WACOM公司生产的一款具有1 024级压力传感器的数位板[12],在手写板上采集到签名的x坐标、y坐标及压力信息,采样的时间间隔Δt为10 ms。采集到的原始真实签名和伪造签名图像及其分别对应的x坐标、y坐标曲线随时间变化示意图如图1~图4所示。

图1 真实签名

图2 伪造签名

图3 真实签名和伪造签名的x轴轨迹曲线
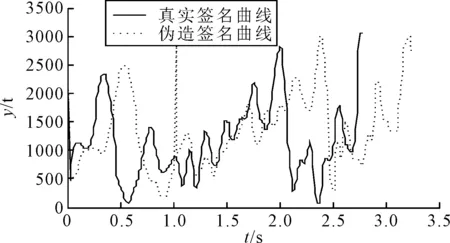
图4 真实签名和伪造签名的y轴轨迹曲线
1.2预处理

笔者采用算术均值滤波法对签名曲线进行平滑,其原理是对待处理的当前数据点ai,选择其左右相邻的两个点ai-1,ai+1,求得这3个值的平均值作为当前点的值。由于需要滤波的数据是一维线性数据,假设采集的原始签名数据有个点,故而选用模版大小为1×3,计算公式如下:
(i=2,3,…,N-1)
(1)
平滑后,由于书写者不能保证每一次签名的大小都一致,因此需要对不同签名进行归一化。计算方法为:
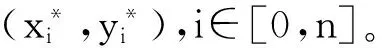
预处理前后的对比如图5~图6所示,预处理可以去除掉一些伪极值点,为更精确地匹配奠定基础。
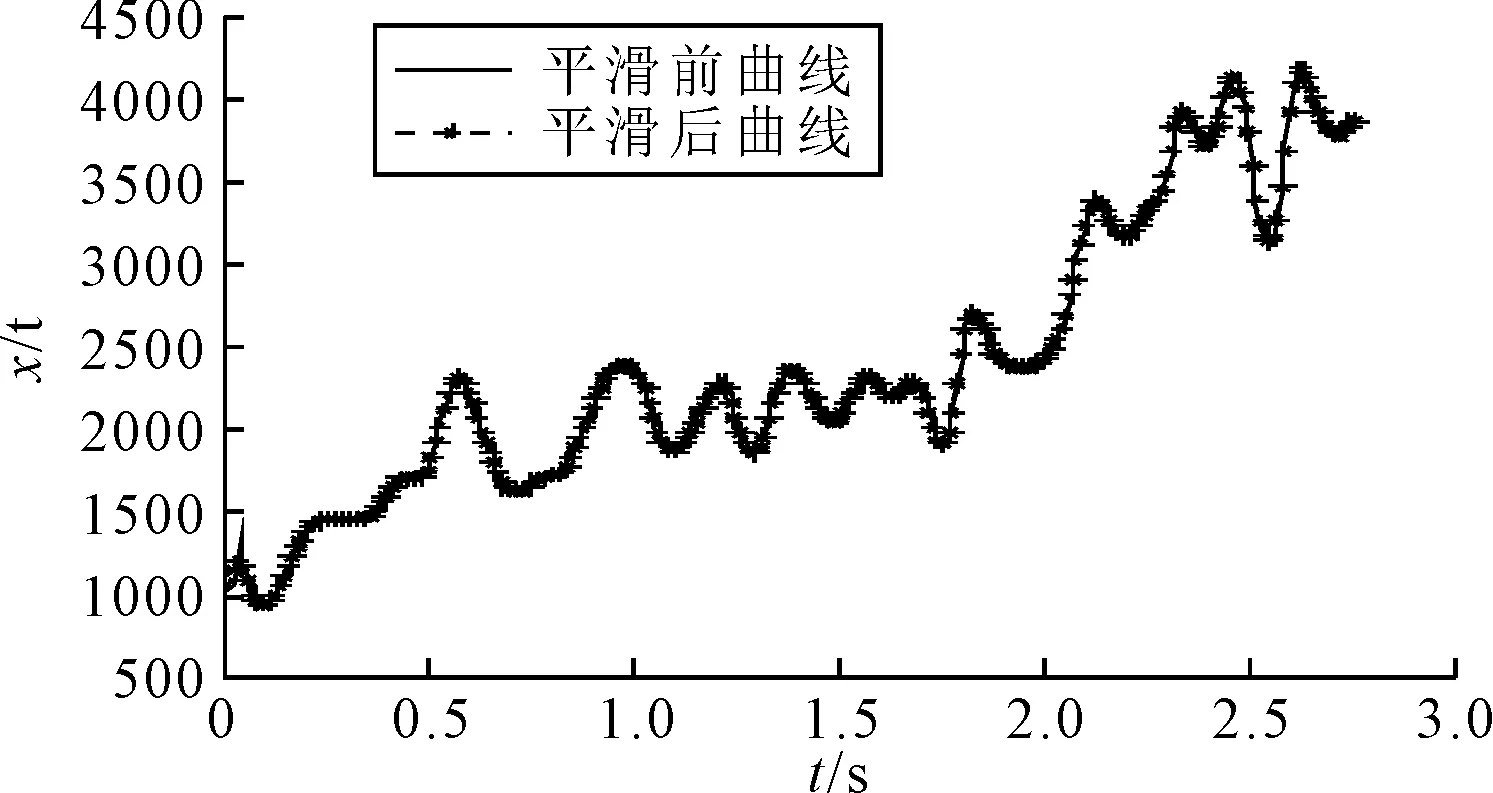
图5 真实签名x轴轨迹曲线预处理前后对比

图6 真实签名y轴轨迹曲线预处理前后对比
1.3特征提取
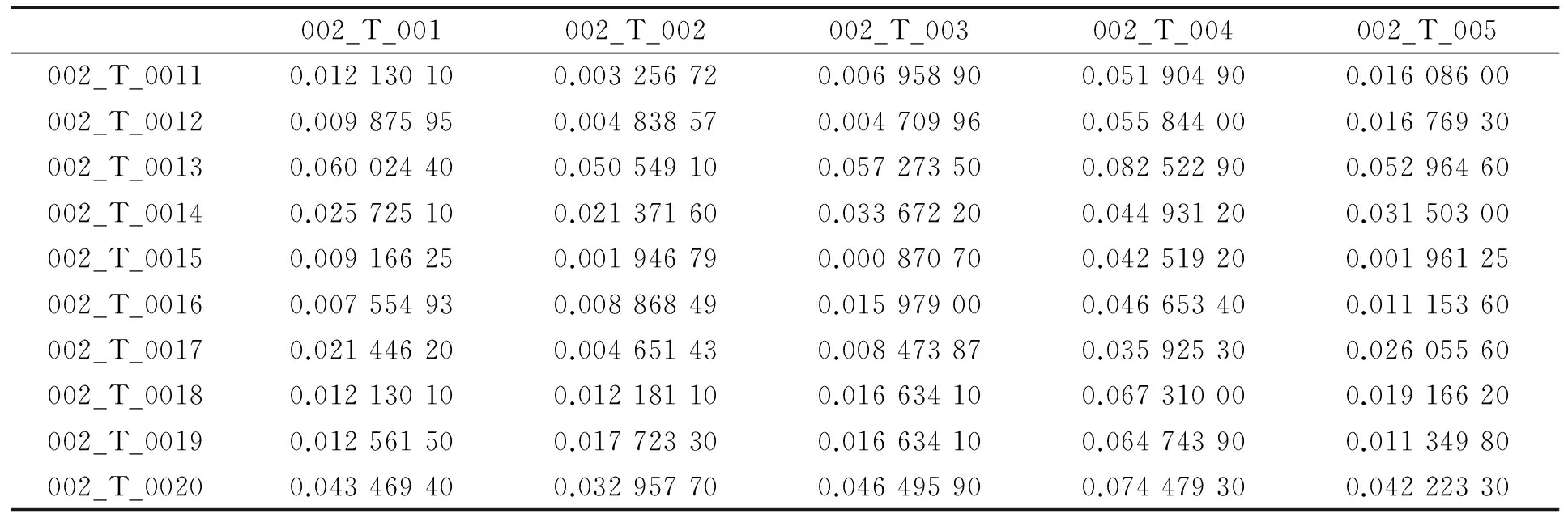
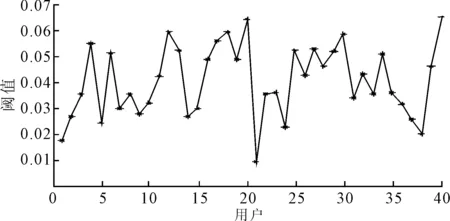
签名曲线中的特征点分为波峰点和波谷点。由于波形曲线是由离散的点构成,故可选取一个点与周围相邻的4个点进行比较并找到稳定极值点。即对于波形中的某个点ai,若ai>ai-1>ai-2且ai>ai+1>ai+2,则ai为稳定的波峰点;对于波形中的某个点ai,若ai 1.4曲率的计算 对于由离散点构成的签名曲线,只能利用某点及其相邻点值来近似估算该点的曲率[15-16]。设k0为曲线T在点p0处的曲率,R0为曲线T在点p0处的曲率半径,即密切圆的半径,则k0=1/R0。密切圆的极限定义为:设p0为曲线T上一点,p1,p2分别为曲线上点p0附近的两点,当p1,p2沿着曲线趋近于点p0时,这3点所确定的圆的极限位置为点p0的密切圆。于是可以利用密切圆构造一种计算离散曲率的方法,用点p0及其附近两点p1,p2确定的圆即Δp0p1p2的外接圆近似代替密切圆。 (3) 利用x轴和y轴曲线的信息,得到的真实签名和伪造签名曲率曲线如图7和图8所示。 图7 平滑后真实签名每点对应的曲率曲线 图8 平滑后伪造签名每点对应的曲率曲线 2.1签名曲线相似性的度量 首先建立如下的一个数学模型:给定两条由极大值点构成的多边形链A=〈a1,a2,…,am〉和B=〈b1,b2,…,bn〉,且m (4) 若两条曲线被判为相似,那么参考签名曲线的第i个波峰点只可能与测试签名对应的第i-1个、第i个、第i+1个波峰点匹配,或不与测试签名的任一波峰点对应匹配,故实际上压缩了搜索空间。这样就有下列7种可能性: 当Ai=〈ai〉,Bi=0时,则有: 当Ai=〈ai〉,Bi=〈bi+1〉时,则有: 当Ai=〈ai〉,Bi=〈bi-1,bi〉时,则有: 2.2新的在线手写签名认证方法 首先对参考签名和测试签名的x轴曲线进行分析,具体步骤如下: (1)将参考签名的m个波峰点和测试签名的n个波峰点作比较,若n-m≥5,则认为这两个签名不相似,算法结束;否则执行步骤(2)。 笔者采用2004年国际签名认证大赛中的评价标准,以SVC2004任务1作为实验数据集对算法进行评估,其包含40位签名者,每个人有20个真实签名和20个伪造签名。首先对每位签名者选取10个真实签名作为训练,另外10个真实签名和10个伪造签名作为测试,分别进行比较算出距离,以第2位用户的签名数据为例,其部分比较结果如表1和表2所示。 表1 5个真实参考签名和10个真实测试签名之间的距离比较 表2 5个真实参考签名和10个伪造测试签名之间的距离比较 在SVC2004数据库的40位用户中,利用每位用户的20个真实签名进行研究来确定阈值。将每一个真实签名都作为模板,分别与其他19个签名作比较,共算出190个不同的离散Fréchet距,再求其平均值,通过大量的实验学习和训练来初步确定不同用户的阈值。其实验结果如图9所示。 对每位用户确定出阈值后,再从每位用户的真实签名中随机选择一个签名作为模板,与剩余样本和伪造样本计算出距离,并与设定的阈值范围进行比较分析,得出签名样本库总的误纳率(FAR)和误拒率(FRR)。笔者选择第2位用户的第2个签名作为模板,其他真实和伪造签名作为测试进行验证,其阈值为0.026 916 70,部分比对结果如表3所示。 图9 40位用户的不同阈值 实验对真实签名数据库的800个数据与伪造签名数据库的800个数据分别进行了测试,其中有1 498个签名匹配成功,成功匹配率为93.625%,其比较结果如表4所示。 表3 部分测试签名和模板签名的匹配情况 表4 FAR与FRR的对比 可以看出有52个伪造签名被误认为真实签名,误纳率FAR为3.250%,还有50个真实签名被误认为伪造签名,误拒率FRR为3.125%,最终总的误判率为6.375%。 目前,模式识别领域的算法被广泛应用于在线签名认证中,很多研究者致力于对已有认证算法的改进和组合,如FUENTES等[19]利用SVM将动态HMM和全局MLP进行融合来认证签名,提高了认证算法的鲁棒性。IRANMANESH等[20]使用多层感知器(MLP)神经网络对签名数据进行分类。一些学者在进行签名性能评估时有使用其建立的数据库,也有使用一些公开的签名数据库如PHILIPS在线签名数据库、SIGMA数据库、SUSIG数据库和SVC2004签名数据库等。如表5所示为使用不同数据库和不同方法的认证性能。 基于SVC2004这个标准数据集,笔者研究了一种新的在线签名认证方法。首先对签名曲线进行预处理,提取出稳定的极值点,并求出特征点的曲率值,再用离散Fréchet距作为距离测度进行签名认证,曲率具有平移和旋转的不变性,在判别签名曲线相似性方面有很好的效果。实验表明,该算法对熟练伪造签名有很好的识别效果,与其他方法相比具有较低的误纳率和误拒率。 表5 系统性能对比 [1] 邱益鸣,胡华成,郑建彬.基于曲线相似的在线签名认证方法[J].系统工程与电子技术,2014,36(5):1016-1020. [2] 王飞,孙锬锋,蒋兴浩.在线签名认证综述[J].信息安全与通信保密,2015(5):107-111. [3] 金涌,柳健.基于空间曲线弹性匹配的在线手写签名鉴别[J].华中理工大学学报,1999,27(5):14-16. [4] 郑建彬,郭震,黄樟灿,等.在线手写签名认证的演化设计[J].计算机工程与应用,2006,42(21):28-31. [5] ZHU Y J, ZHOU L S, WANG J. Contour extraction and feature point detection for 3-D fragments reassembly[J]. Transactions of Nanjing University of Aeronautics and Astronautics,2005,22(1):25-29. [6] ZHU Y J, ZHOU L S, ZHANG L Y. Algorithm for three-dimensional fragments reassembly[J]. Journal of Image and Graphics,2007,12(1):174-170. [7] LIU S S, ZHU Y J, ZHANG L Y. Research on algorithm for matching 2D contours[J]. Electrical Technology and Automation,2005,34(2):60-63. [8] ZHOU S L, LIAO W H, YIN J P. Study of method for planar fragmented objects matching[J]. Computer Engineering and Application,2009,45(31):151-153. [9] HOLM L, SANDER C. Mapping the protein universe[J]. Science,1996,273(5275):595-602. [10] EFRAT A, FAN Q F, VENKATASUBRAMANIAN S. Curve matching, time warping and light fields: new algorithms for computing similarity between curves[J]. Journal of Mathematical Imaging & Vision,2007,27(3):203-216. [11] 罗琼.智能手机在线手写签名认证系统设计[D].武汉:武汉理工大学,2014. [12] 高伟霞,韩新风,张永峰.在线签名认证的数据采集系统设计[J].吉首大学学报(自然科学版),2012(4):91-94. [13] 王飞.基于HMM/ANNs混合模型的视频手写签名认证算法的研究与实现[D].上海:上海交通大学,2015. [14] 李成华,龚良慧,江小平,等.基于EMD和SVD的在线手写签名特征提取方法[J].中南民族大学学报(自然科学版),2016,35(1):103-107. [15] 方丽菁,卢卫君,黄文钧.曲率挠率的估计算法及其工艺嵌入[J].图学学报,2012(2):9-13. [16] 于昊,赵乃良,陈小雕.类曲率在曲线相似性判定中的应用[J].中国图象图形学报,2012,17(5):707-714. [17] 安霄霄.手写签名的多重数字水印及认证算法研究[D].哈尔滨:哈尔滨工业大学,2015. [18] 朱洁,黄樟灿,彭晓琳.基于离散Fréchet距离的判别曲线相似性的算法[J].武汉大学学报(理学版),2009(2):227-232. [19] FUENTES M,GARCIA S S, DORIZZI B. Online signatureverification: fusion of a hidden markov model and a neural network via a support vector machine[C]∥Ninth International Workshop on Frontiers in Handwriting Recognition.[S.l.]:[s.n.],2002:253-258. [20] IRANMANESH V, AHMAD S M S, ADNAN W A W, el al. Online handwritten signature verification using neural network classifier based on principal component analysis[J]. The Scientific World Journal,2014,1155(10):381469-381476. TAN Hua:Postgraduate; School of Science, WUT, Wuhan 430070, China. On-line Signature Verification Based on Curvature TANHua,HELang,HUANGZhangcan,FANGXuansu,WANGFeiyang In order to improve the accuracy of signature verification, a new feature extraction and distance measurement method are proposed. Firstly, the signature curve is preprocessed. Secondly, curvature values of extreme points are calculated. Finally, it is based on discrete Fréchet distance that signature verification algorithm is designed, compared with other distance measures, discrete Fréchet defines the point correspondence between two point sets to improve the accuracy of curve similarity judgment. Experiments show that the algorithm has less time complexity, and has a lower FAR and FRR. signature verification; extreme points; curvature; discrete Fréchet distance; curve similarity 2095-3852(2017)01-0115-06 A 2016-08-14. 谭华(1990-),女,湖北咸宁人,武汉理工大学理学院硕士研究生. 国家科技支撑计划基金项目(2013BAJ02B00). TP391.43 10.3963/j.issn.2095-3852.2017.01.024
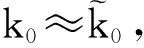


2 算法设计

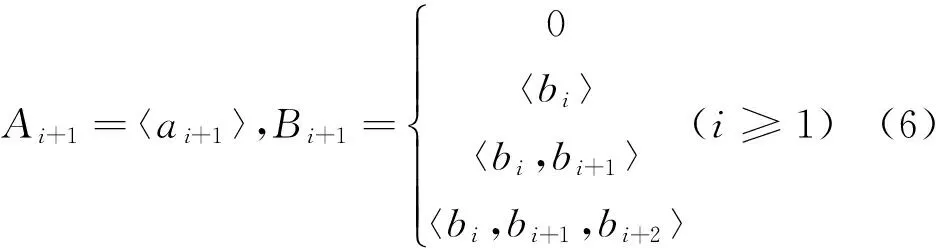







3 实验结果与分析



4 结论


