基于三方相互威慑讨价还价模型的PPP项目风险分担
张 瑞,张义祝
(1.河海大学 工程管理研究所,江苏 南京 210000;2.连云港市市区水工程管理处,江苏 连云港 222002)
基于三方相互威慑讨价还价模型的PPP项目风险分担
张 瑞1,张义祝2
(1.河海大学 工程管理研究所,江苏 南京 210000;2.连云港市市区水工程管理处,江苏 连云港 222002)
现有的PPP风险都是在“政府”与“私人部门”之间进行分担,并未考虑风险在“私人部门”内部之间的分担。为此,构建政府部门、项目公司中专业公司和纯投资者三方相互威慑讨价还价模型,并得出相对应的子博弈纳什均衡。使得项目风险在“政府”和“私人部门”之间合理分担的同时也可以在“私人部门”内部间得到合理分配,该项成果不仅在理论上补充了现有PPP风险分担存在的不足,而且为我国后续PPP项目进一步发展提供了较好的基础。
PPP项目;风险分担;三方讨价还价模型
随着我国经济的不断发展及城市化进程的加剧,政府建造的基础设施项目不能满足人民需求的这一矛盾,日益凸显。为了解决该矛盾,PPP这种新型融资项目应运而生并得到迅猛发展。PPP是一种合作机制,在这种机制下政府和私人部门在享受不同权利和义务的同时通过相互合作发挥互补能力,从而可以提供更高效的基础设施产品和公共服务[1]。然而PPP项目具有投资额巨大、持续时间长、合同不完备程度高等特点,这使得双方在项目实施过程中存在诸多不确定风险,对这些风险因素如何进行合理的分担成为双方谈判的重点和难点。不合理的风险分担方式不仅会导致项目投资成本增加、工期拖延,甚至会导致项目失败,与此同时实践过程中PPP项目参与者谈判重点是如何进行风险合理的分配[2]。因此,如何进行风险的合理分配就是PPP学者研究的热点。
目前关于PPP风险分担问题的研究主要采用的是定性研究,包括风险分担的研究机理、原则等。在风险分担准则方面,王丙亮等提出风险分担的原则:①风险应由最有能力掌控风险后果的部门承担,②风险应由能以最小成本承担风险的部门承担[3];陈波等提出风险分担的准则为:①风险共担原则,②由最有控制力一方承担,③承担风险要和获得收益相匹配,④风险有上限[4];郑彦璐等提出风险分担的原则为风险与控制力相对称、风险与收益相对称原则和上限原则[5];王雪青等在将PPP项目风险分为宏观、中观、微观风险的基础上,依据参与方对风险的偏好不同将风险分配给最适合的一方承担[6]。在风险分担的框架体系方面,程连于构建了蒙特卡罗模拟为基础的风险评估与优化框架体系,验证了在随机发生不定风险时,按照最低可行价格进行风险分担是合理可行的[7];李丽红等在分析我国PPP发展现状的基础上,发现PPP项目的服务效率、风险控制成本及风险分担之间存在一个合理的区间,并进一步构建了风险分担的框架[8];杜亚灵等提出PPP风险分担研究的3种主要途径为理论推演、理论应用和实践总结,并且提出风险分担比例的确定是当前PPP研究的主要薄弱环节[9]。在PPP项目风险分担研究方面,El-SAYEGH通过问卷调查从而确定一个适当的风险分担比例[10];范小军等针对双方需要共同承担的融资风险,分别从影响项目成本和项目收益角度构建了风险分担比例模型[11];周鑫构建了政府部门和私人部门双方讨价还价模型,使用贴现率来确定风险分担的比例[12];朱向东等将风险分担的主体从两方拓展到三方,并构建了三方静态博弈模型[13];李林等根据参与方地位不对称构建了完全信息和不完全信息的双方讨价还价模型,并求出纳什均衡解[14];何亚伯等为了克服层次分析法主观性过强问题,构建了基于AHP和熵值法的PPP风险分担模型[15]。
相互威慑讨价还价是在20世纪60年代被托马斯用来描述美苏两个国家之间关系,并且其将讨价还价能力定义为能给对方带来伤害的能力,但该说法并没有在学术界得到认可;30年后阿里尔鲁宾斯坦从非合作博弈角度求解了具有时间偏好的完全信息无限期讨价还价惟一完美均衡解;向钢华等首次将不完全信息引入相互威慑讨价还价模型中,建立了不完全信息的相互威慑讨价还价模型[16];龚志强等提出了三方相互威慑讨价还价模型并给出均衡解[17]。
对上述文献整理后可以发现,现有的PPP风险分担研究主要为风险分担的原则、机理、框架的定性研究[18],定量研究尤其是风险分担比例确定的研究较少,并且在进行风险分担时一般都在政府部门和私人部门两方之间进行分担,但风险在私人部门与政府部门分配之后,私人部门内部如何进行风险分担,现有文献几乎没有涉及。笔者希望构建政府部门、项目公司中专业公司和纯投资者三方相互威慑讨价还价模型,从而使得风险在政府部门和私人部门之间合理分配之后,也可以使得风险在项目公司内部得到合理分配,从而提高项目的成功率。
1 PPP项目参与者讨价还价的过程描述
1.1PPP项目参与者
PPP项目涉及众多参与者,主要包括政府部门、各方纯投资者、承包商、监理单位、供货方、保险公司、担保方及最终使用者。PPP项目众多参与方最少可以分成3类:政府各部门、项目公司中纯投资者及项目公司中专业公司。以上项目三方参与者能否对PPP项目的各类风险进行合理分配是关系项目成败的重要因素。
1.2PPP项目三方讨价还价的过程
在PPP项目的三方参与者讨价还价过程中,为了实现己方利益最大化往往会暂时性选择自发性的联合,笔者称此类行为为“联盟”,因为两方“联盟”后对另外一方的威慑力大大增强,可以使“联盟”得到更多的利益,得到的利益最后在“联盟”的双方间进行分配。在现实中,与政府部门相比,项目公司中专业公司和纯投资者都处于弱势地位,由项目公司中专业公司和纯投资者组建SPV统一和政府部门谈判,进行风险分担,按照Rubinstein的讨价还价模型轮流进行出价,最终达到均衡,从而实现PPP项目风险在三方间分配。
博弈过程[19-20]根据参与方信息掌握的程度可分为完全信息博弈过程和非完全信息博弈过程。完全信息博弈是指在博弈过程中,每一位参与人对其他参与人的特征、策略空间及收益函数有准确的信息;不完全信息博弈是指参与人对其他参与人此类信息不能完全掌握。
2 不完全信息条件下PPP项目风险的初次分配
笔者采用三方相互威慑讨价还价模型,在模型中,与政府部门相比,项目公司中专业公司和纯投资者处于相对弱势地位,所以在第一轮讨价还价中,项目公司中专业公司和纯投资者为了更好“抵御”政府方的威慑以获取己方利益最大化,项目公司中专业公司和纯投资者会率先组成“联盟”和政府进行讨价还价。
2.1基本假设
假设1 政府和“联盟”都是理性的,均不希望谈判破裂。
假设2 政府和“联盟”间的信息是不对称的,也就是说在谈判过程中,由于双方的地位和信息获取不同,某种风险对于一方得利与否不确定。
假设3 风险都是相互独立,每一类风险和其他风险没有关联。
假设4 对于某种风险,假设一方承担的比例为Ki,则另一方承担的比例为1-Ki,双方对Ki的大小进行讨价还价。
假设5 相比于“联盟”,政府占据优势地位,由政府先出价。
2.2模型参数的讨论
(1)谈判损耗系数δ。该模型中最重要的一个因素就是谈判损耗系数δ(δ>1),也就是每多进行一次谈判过程,双方都会消耗一定的谈判成本,主要包括双方付出的时间、可能错过投资而造成的收益损失及收齐信息花费的成本。因此,在讨价还价过程中,每多进行一轮博弈双方承担的成本损失就越大,风险也就越大。在实际PPP项目中,由于政府和“联盟”所处的地位是不对等的,所以每多进行一个回合谈判,存在δ1(政府损耗系数)<δ2(“联盟”损耗系数),也就是说对于“联盟”而言,每多进行一轮谈判造成的损失比政府部门大。
(2)海萨尼转换。在1967年以前,博弈论专家认为不完全信息博弈是没有办法研究的,因为当一个参与人不知道与谁博弈时,博弈的规则是无法定义的。但是1967年海萨尼提出解决不完全信息博弈的方法是,引入一个虚拟的参与人—“自然”,“自然”首先行动决定参与人的特征,参与人知道自己的特征,其他参与人不知道,这样不完全信息博弈就转变为完全但不完美信息博弈,这就是所谓的“海萨尼转换”,后来海萨尼已经成为处理不完全信息博弈的标准方法。
(3)公共部门强势的概率。政府在谈判过程中不知道“联盟”在谈判中的强弱地位,政府是理性人不希望谈判破裂,希望尽快达成协议,政府部门将以概率q1的可能性采取强势威慑“联盟”承担更多的风险,以概率q2的可能性不采取强势威慑“联盟”承担更多的风险(其中q1+q2=1)。
2.3模型的构建
该模型中政府部门比“联盟”更加具有优势地位,所以由政府部门先“出价”。

(1)
(2)
政府部门以概率为q2(q1+q2=1)的可能性不威慑“联盟”转移自己的风险比例,则在此种情况下政府部门承担的风险G″1和“联盟”承担的风险U″1分别为:
G″1=q2K1=(1-q1)K1
(3)
U″1=q2(1-K1)=(1-q1)(1-K1)
(4)
第一回合中政府和“联盟”承担的风险期望值分别为:
(1-q1)K1
(5)
(1-q1)(1-K1)
(6)
同理可得第二回合中政府和“联盟”承担的风险期望值分别为:
G2=q1δ1(K2-α2)+
δ1(1-q1)K2
(7)
U2=q1δ2(1-K2+α2)+
δ2(1-q1)(1-K2)
(8)
第三回合政府部门和“联盟”承担的风险期望值分别为:
(9)
(10)
政府部门和“联盟”讨价还价的过程将一直持续下去直至双方对风险承担的比例达成一致。
2.4模型的求解
经过海萨尼转换以后,对于无限期讨价还价模型而言,设立的逆推归纳点无论在第三回合还是第一回合,结果都是一致的,所以笔者选择无限期讨价还价模型的第三回合作为逆推起点。第二回合中,假如“联盟”提出的风险承担比例使政府在第二回合承担的风险期望值G2大于政府在第三回合承担的风险期望值G3,则政府部门肯定会拒绝“联盟”在第二回合提出的风险承担比例K2,每进行一次谈判“联盟”都会承担谈判损耗并且在现实情况下“联盟”的谈判损耗(δ2)会大于政府部门的谈判损耗(δ1),为了避免谈判被拖入第三回合而造成自己谈判损耗的增加,“联盟”在第二回合提出的风险分担比例时,在使己方承担的风险期望值最小的情况下,同时要使政府部门在第二回合承担的风险期望值G2不大于政府部门在第三回合承担风险的期望值G3,那么“联盟”在第二回合提出的最优策略是:
G2=G3
(11)
q1δ1(K2-α2)+δ1(1-q1)K2=
(12)
K2=δ1K3+q1α2-q1δ1α3
(13)
在这种情况下,“联盟”第二回合和第三回合承担的风险期望值分别为:
U2=δ2(1-δ1K3+q1δ1α3)
(14)
(15)
U2-U3=δ2(1-δ1K3+q1δ1α3)-
(16)
U2-U3=δ2[(1-δ2)-(δ1-δ2)(q1α3-K3)]
(17)
因为δ2>δ1>1,0 现在逆推到第一回合,如果政府部门在第一回合提出的风险分配比例使“联盟”在第一回合承担的风险期望值U1大于“联盟”在第二回合承担的风险期望值U2,则“联盟”肯定会拒绝政府部门在第一回合提出的风险分担比例,谈判进入第二回合,每多进行一次谈判,政府部门都会增加谈判损耗,所以政府部门也不想将谈判拖入第二回合,因此政府部门在第一回合提出的风险承担比例是:在己方第一回合承担风险的期望值最小的基础上,同时让“联盟”在第一回合承担风险的期望值U1不大于“联盟”在第二回合承担风险的期望值U2,那么政府部门在第一回合的最优策略为: U1=U2 (18) q1(1-K1+α1)+(1-q1)(1-K1)= δ2(1-δ1K3+q1δ1α3) (19)K1=1+q1α1-δ2+δ1K3δ2-q1δ1α3δ2 (20) 该模型是无限次讨价还价模型,对于一个无限次讨价还价模型而言,无论是从第一回合还是从第三回合开始,结果都是一样的,可得: K1=K3 (21) K3=1+q1α1-δ2+δ1K3δ2-q1δ1α3δ2 (22) K3=[δ2-1+q1(δ1α3δ2-α1)]/(δ1δ2-1) (23) 1-K3=[δ1δ2-δ2+q1α1+q1δ1α3δ2]/(δ1δ2-1) (24) 假设αi为常数,则政府部门和“联盟”承担风险的均衡结果分别为: K=(δ2-1)/(δ1δ2-1)+q1α 1-K=(δ1δ2-δ2)/(δ1δ2-1)-q1α 由上式可知,K是政府部门的风险报价,由于政府部门有q1的可能威慑“联盟”将属于己方风险额α转移给“联盟”,所以政府部门实际承担的风险比例为(δ2-1)/(δ1δ2-1),而“联盟”实际承担的风险比例为(δ1δ2-δ2)/(δ1δ2-1)。 笔者已经进行了“联盟”和政府部门的风险分担比例进行分配,接着将进行风险在“联盟”内部的风险分配,项目公司中专业公司和纯投资者为了利益最大化双方组成“联盟”时已经进行了信息的公开,所以风险在纯投资者和专业公司进行分配时的信息是对称的,所以此时风险分担博弈是完全信息条件下讨价还价模型。 3.1基本假设 假设1 为了在和政府博弈中得利,纯投资者和专业公司完全了解公开信息,因此信息是对称的。 假设2 纯投资者和专业公司间都是理性的,均不希望谈判破裂。 假设3 风险都是独立的,彼此间无关联。 假设4 某一种风险(纯投资者和专业公司承担的风险比例为β,0≤β≤1),纯投资者承担的比例为γi,则专业公司承担的比例为β-γi,双方对γi进行讨价还价。 假设5 相对于专业公司而言,纯投资者更具主导地位,所以由纯投资者先出价。 3.2模型的构建 (25) (26) 专业公司对于纯投资者提出的风险分担比例可以有两个选择,接受或者拒绝,如果专业公司接受纯投资者提出的风险分担比例则讨价还价到此结束,否则进入下一回合。 同理可得,第二回合纯投资者和专业公司承担的风险期望值分别为: (27) (28) 第三回合纯投资者和专业公司承担的风险期望值分别为: (29) (30) 3.3模型的求解 B2=B3 (31) (32) (33) 在这种情况下,专业公司在第二回合承担的风险期望值为: (34) (35) P1=P2 (36) (37) (38) 对于一个无限次讨价还价模型而言,无论是从第一回合还是第三回合逆推结果都是一致的,可以得到: γ1=γ3 (39) (41) (42) (43) 其中β=(δ1δ2-δ2)/(δ1δ2-1),则: (44) (45) 综上所述,政府部门、专业公司和纯投资者分担的风险比例分别为: 政府部门 (δ2-1)/(δ1δ2-1) 合理的风险分担是PPP项目成败的关键因素,以往的研究将PPP项目的风险仅在“政府部门”和“私人部门”之间进行分担,并没有考虑“私人部门”构成的多样性、对待风险的偏好及应对能力不同。笔者通过比较以往对于PPP风险分担比例的研究,从而构建了政府部门、纯投资者、项目公司中专业公司三方相互威慑讨价还价模型,使得风险在“政府”与“私人部门”进行合理分担的同时,风险也可以在“私人部门”间得到合理的分担。对于笔者最终提出的风险分担比例,是考虑纯投资者和项目公司中专业公司之间进行合作共同“对抗”政府部门得出的比例,实际过程中具体情况还需要进一步研究。研究发现只有当项目公司中专业公司和纯投资者之间进行合作才可以利益最大化;与此同时,政府部门最优策略是打破纯投资者和项目公司中专业公司之间的合作。由于条件的限制,笔者最终结论中的谈判损耗系数的确定是通过问卷调查和访谈得到,并且接受问卷和访谈的人均有过多次参与PPP项目的建设,以求结果更可靠,希望笔者的研究结果可以弥补PPP项目在风险分担方面不足,并为PPP项目的风险分担提供一个依据。 [1]JINXH,DOLOH.Interpretingriskallocationmechanisminpublic-privatepartnershipprojects:anempiricalstudyinatransactioncosteconomicsperspective[J].ConstructionManagementandEconomics,2008,26(7):707-721. [2]LIB,AKINTOYEA,EDWARDSPJ,etal.TheallocationofriskinPPP/PFIconstructionprojectsintheUK[J].InternationalJournalofProjectManagement, 2005,23(1):25-35. [3] 王丙亮,游锐.大型基础设施建设PPP项目风险分配研究—修正最终要约仲裁的引入[J].经济论坛,2009(21):126-128. [4] 陈波,徐成桂.PPP融资模式的风险分配方法[J].交通科技与经济,2011,13(1):126-128. [5] 郑彦璐,邓小鹏,李启明.保障性住房PPP模式的风险分配理论分析[J].东南大学学报(哲学社会科学版),2010,12(6):22-25. [6] 王雪青,喻刚,邴兴国.PPP项目融资模式风险分担研究[J].软科学,2007,21(6):39-42. [7] 程连于.PPP项目融资模式的风险分担优化模型[J].价值工程,2009,28(4):142-145. [8] 李丽红,朱百峰,刘亚臣,等.PPP模式整体框架下风险分担机制研究[J].建筑经济,2014(9):11-14. [9] 杜亚灵,尹贻林.PPP项目风险分担研究评述[J].建筑经济,2011(4):29-33. [10]El-SAYEGHSM.RiskassessmentandallocationintheUAEconstructionindustry[J].InternationalJournalofProjectManagement,2008,26(4):431-638. [11] 范小军,赵一,钟根元.基础项目融资风险的分担比例研究[J].管理工程学报,2007,21(1):98-101. [12] 周鑫.PPP项目融资风险分担博弈分析[J].合作经济与科技,2009(14):78-79. [13] 朱向东,肖翔,征娜.基于三方博弈模型的轨道交通项目风险分担研究[J].河北工业大学学报,2013(2):97-101. [14] 李林,刘志华,章昆昌.参与方地位非对称条件下项目风险分配的博弈模型[J].系统工程理论与实践,2013,33(8):1940-1948. [15] 何亚伯,孙蕾,秦伟.基于AHP和熵值法的PPP项目风险分担研究[J].项目管理技术,2016(14):35-41. [16] 向钢华,王永县.一种不完全信息相互威慑讨价还价模型[J].运筹与管理,2008,17(6):16-19. [17] 龚志强,谢政,戴丽.三方相互威慑讨价还价模型[J].经济数学,2015(2):87-92. [18] 吕俊修,刘冬梅.PPP融资项目中风险分担的操作[J].工程建设与设计,2009(5):115-119. [19] 张维迎.博弈论与信息经济学[M].上海:上海人民出版社,2012:24-56. [20] 谢识予.经济博弈论[M].上海:复旦大学出版社,2002:114-159. ZHANG Rui:Postgraduate; School of Business, Hohai University, Nanjing 211100, China. Risk Sharing of PPP Project Based on Three Parties Mutual Deterrence Bargaining Model ZHANGRui,ZHANGYizhu The existing PPP risks are shared between government and private sector,the sharing of risk within the private sector is not considered. This paper constructs the government,the project company professional company and investors tripartite mutual threat bargaining model, and acquire the corresponding sub game Nash equilibrium. The risk between the government and private sector can share reasonable and meanwhile the inner of private sector can also get reasonable share , the results not only supplement the problems concerned with the existing PPP risk sharing in theory but also for the follow-up of the PPP projects provide a good foundation for further development. PPP project; risk sharing; three parties bargaining model 2095-3852(2017)01-0054-06 A 2016-08-12. 张瑞(1992-),男,江苏宿迁人,河海大学商学院硕士研究生. C931 10.3963/j.issn.2095-3852.2017.01.0123 完全信息条件下PPP项目风险的再次分配
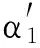

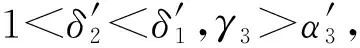
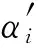
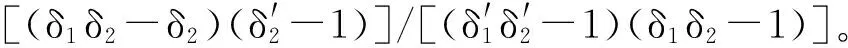


4 结论

