带时间窗的突发灾害应急物流中心选址研究

孙 强

(辽宁工程技术大学 工商管理学院，辽宁 葫芦岛 125105)

带时间窗的突发灾害应急物流中心选址研究

孙 强

(辽宁工程技术大学 工商管理学院，辽宁 葫芦岛 125105)

为提高应急救援的时间满意度，建立了基于救援时间满意度的突发灾害应急物流中心选址优化模型，并利用改进的人工蜂群算法对模型进行运算。结果表明，改进的人工蜂群算法能对应急物流中心的选址和救援地的物资需求量进行有效计算，且能对不同救援地的时间满意度进行求解。与不带时间窗的突发灾害应急物流中心选址模型相比，该模型同时满足了应急救援成本的最小化和救援时间满意度的最大化。

突发灾害；应急物流中心选址；救援时间窗；救援时间满意度；改进人工蜂群算法

突发灾害是指突然发生的、造成或可能造成严重社会危害, 需要采取应急处置措施予以应对的自然灾害、事故灾难、公共卫生事件和社会安全事件[1]。目前我国正处在社会经济发展的关键时期，各类突发事件时有发生，且呈现出一系列新的特点[2]。当突发自然灾害发生时，如何科学有效地配置应急资源，避免灾难进一步扩大，具有重要的理论意义和应用价值，物流中心的优化选址与救援时间满意度是突发灾害应急救援考虑的首要因素。SUN 等将模糊粗糙集理论引入到应急物流模型中，运用运筹学的方法对模型进行求解，并用实例验证了模型与算法的有效性[3]。刘北林等综合考虑应急物流的时间性和救援活动的经济性，建立了多目标数学模型并利用TOPSIS法对模型进行求解[4]。赵明等以多供应点多受灾点的应急物资调度为研究对象，以开始时间最早和救援地数目最少为目标构建了调度模型，并用遗传算法对其进行了求解[5]。宋晓宇等引入灰色理论研究了非匀速连续消耗的多物资供应点选择问题[6]。ALEM等研究救灾过程中物流中心的随机规划模型，为应急物流的配送决策提供了新的思路[7]。HE等考虑应急救援中的不确定性，建立了基于公众利益最大化的应急医药物流规划模型，为救援物资的储备提供了理论基础[8]。

现有研究存在的问题有：①目标函数多集中于救援成本最小化，对时间要素在应急物流中的作用少有考虑，这容易导致应急救援的及时性受到影响；②没有考虑到救援地对救援活动的时间满意度，导致应急物流中心的选址考虑因素不全面；③对应急物流中心的水平物流活动，相关研究较少。基于此，笔者将应急物流的时间因素考虑在内，根据不同救援地的时间满意度要求，建立了包括时间成本和物流成本在内的突发灾害应急物流中心选址模型，以实现应急物流中心的合理选址和救援时间满意度的最大化。

1 突发灾害应急物流中心选址模型

1.1问题描述

笔者研究的是基于三级物流网络的突发灾害应急物流救援模型：救灾物资供应中心、应急物流中心、救援地。突发灾害事件发生时，应急物流起始于救灾物资供应中心，这是一个持续获得救援物资并随时准备分拨的应急物资集散地，所有救灾物资均从这里出发配送。应急物流中心属于联系救灾物资供应中心和救援地的桥梁，除了向救援地分配物资外，还具有水平调拨物资的作用，共同保证在最短的时间内将救援地需要的救援物资送达，应急物流中心的合理选址是保障救援绩效和救援时间满意度的前提。

1.2救援时间满意度

应急救援时间的早晚决定了被救援群众的生命是否安全，因此救援地对于应急救援物流的时间有较高要求，在有效的时间段内，救援物资越早送达救援地，救援时间满意度就会越高[9]。将救援时间满意度函数引入突发灾害应急物流中心选址模型，可以最大限度地提高救援的时间满意度[10]。设救援时间满意度在[0，1]区间内，救援物资越早送达，救援时间满意度越高。令tjn为j应急物流中心到n救援地的时间，Ljn为n救援地可以等待的最短时间，Ujn为n救援地可以等待的最长时间，于是n救援地对应急物流救援的等待时间范围为[Ljn,Ujn]，λ(tjn)为n救援地对j应急物流中心的救援时间满意度函数：

其中，k为救援时间敏感系数。

1.3模型符号定义

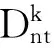
1.4模型构建

目标函数为出现突发灾害时，在保证救援时间满意度的情况下，最大限度地完成救援任务，实现应急救援成本的最小化。该救援过程产生的成本包括应急物流成本和由于救援时间延迟产生的成本两部分，其中应急物流成本包括应急物流中心建设成本、应急物流运输成本、应急物流中心的水平转运成本。

s.t.

(1)

(2)

(3)

(4)

(5)

(6)

wjnYjnt≤tjn

(7)

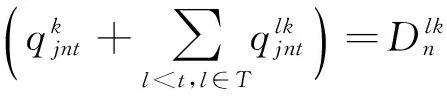
(8)

Yjt∈(0,1)

(9)

Yjnt∈(0,1)

(10)

(11)

∀j∈J,m∈J,n∈N,l

式(1)表示救援地的物资需求能够通过应急物流中心满足；式(2)表示从应急物资供应中心调出的救灾物资不超过其总供应能力；式(3)表示从应急物流中心到救援地的物资不超过其总供应量；式(4)表示应急物流中心之间水平调度的救灾物资均到达救援地；式(5)和式(6)表示应急物流中心的所有救灾物资均全部发出；式(7)表示救援地对救援物流的时间满意度；式(8)表示从应急物流中心发出的配送延迟的救灾物资没有超出救援地可以等待的最长时间；式(9)和式(10)分别表示Yjt和Yjnt为(0,1)变量；式(11)为各变量要满足非负条件；式(12)为各参数的取值范围。

2 模型求解

上述模型为多重约束的混合整数非线性多目标决策模型，可以采用启发式算法对模型进行求解。人工蜂群算法(artificial bee colony algorithm,ABC算法)是一种全新的智能优化算法，具有易于实现、控制参数少、计算简便等优点[11]。ABC 算法中蜂群活动由蜜源、雇佣蜂和非雇佣蜂3部分组成，非雇佣蜂包括观察蜂和侦察蜂两种个体。在求解函数优化问题时，模拟实际蜜蜂采蜜机制处理函数优化问题，每个蜜源的位置代表函数的一个可行解，蜜源的含蜜量对应函数解的适应度值，蜂群寻找蜜源的过程即为算法寻找最优解的过程[12]。ABC 算法常用于解决函数离散优化和无约束优化问题，但雇佣蜂和观察蜂在局部搜索过程中的盲目性和随机性降低了算法的搜索效率和收敛速度[13]。笔者采用文献[14]提出的改进人工蜂群算法，在雇佣蜂寻优过程中引入混沌变量，可以提高雇佣蜂的局部搜索能力；同时采用自适应步长的观察蜂搜索模式，对观察蜂局部搜索行为中的不足进行改进。改进人工蜂群算法流程如图1所示。

图1 改进人工蜂群算法流程

3 算例仿真与结果分析

算法的实现采用Matlab7.0 编写代码，在CPU为3.0 GHz，内存为4G的个人笔记本电脑上进行测试。为验证模型和算法的合理性和科学性，设置算法的具体参数如下：蜜源数量、观察蜂、雇佣蜂、侦查蜂的数量都为100，混沌序列长度为30，向量维度为30，最大迭代次数为1 000，进化停滞阈值参数为100，最大步长为1，最小步长为0.000 1。模型的参数如下：救灾物资供应中心个数为1，应急物流中心个数为4，救援地个数为10，救灾时段为4，救援地可以等待的最短时间为8 h，救援地可以等待的最长时间为24 h，救灾物资类别数为2，体积分别为140 m3和80 m3。救灾物资采用汽车运输，单位运输成本均为1元/(kg·km)，其余参数的取值见表1～表4。

表1 救灾物资在不同救灾时间段的供应能力

表2 不同救灾时间段各救援地对不同救灾物资的需求数量

表3 建立应急物流中心的固定成本和容量

利用改进人工蜂群算法求解时间窗约束的应急物流中心选址优化模型Ⅰ，结果如表5所示。可以看出，模型Ⅰ的目标函数值为2 663 000元，与不带时间窗的应急物流中心选址优化模型Ⅱ相比，无论是从总成本还是延迟成本来看，均优于模型Ⅱ。但模型Ⅰ的物流成本高于模型Ⅱ，这是因为应急物流中心之间的水平物流活动，导致了物流成本的增加，但能使救援地延迟配送的物资数量最少，从而确保了救援地的时间满意度，由成本增加带来的救援效益也是显而易见的，该结果能够说明模型的优越性和可行性。

表4 延迟配送成本

表5 模型结果对比

图2所示为不同救援周期内应急物流中心的位置和救援地的物资配送数量。可以看出，应急物流中心的选址在不同救援周期内，由于救援地的灾情和需求的不同，呈现出动态变化的现象。这样可以在不同的救援周期内，根据应急物流中心的位置和救援地的实际情况，合理选择救援地，最大限度地提高救援效率和救援地的时间满意度。

每个救援地的救援时间满意度结果如表6所示。救援地2因为存在救援延迟的情况，导致该地区的救援时间满意度最低。其余救援地的救援时间满意度均较高。

图2 不同救援周期内应急物流中心选址和救援地的物资配送数量

表6 10个救援地的救援时间满意度

综上，笔者建立的模型具有极大的柔性，无论是救援地的时间满意度，还是应急物流中心的水平调度，在实际应急救援中都是非常必要的，可以保证应急救援各个时期内最大限度地满足救援地的物资需求，使得救援地的延迟配送成本最小化，同时使得救援地的时间满意度和救援总成本最优，为应急物流中心选址和救灾物资分配提供了科学依据。

4 结论

笔者将救援时间满意度引入灾害应急物流中，对带有时间窗的应急物流中心选址进行了研究，采用改进人工蜂群算法对建立的模型进行求解，得出如下结论：①考虑到应急物流中心资源的水平调度，同时考虑了延迟救援成本和救援时间满意度，以各项成本最优为目标，建立了突发灾害应急物流中心选址模型。结果表明，该模型能够科学合理地为突发灾害应急物流中心选址提供理论依据。②采用改进人工蜂群算法对模型进行求解，验证了算法的有效性和可行性。运算结果显示，模型可以很好地考虑到各种突发情况，在保证救援地全覆盖的情况下，最大限度地提高救援时间满意度和降低配送延迟成本，实现救援效益的最大化。③突发灾害应急物流复杂系统影响因素众多，建立的优化模型的目标函数和约束条件都较为简化，并未考虑实际救援中的道路运输条件、救援半径、救援人员的应急响应速度、应急物流中心的周围环境等因素，该模型还需要在实际中进一步具体完善。

[1] 万波,万敏.基于备用覆盖的应急服务设施选址问题研究[J].武汉理工大学学报(信息与管理工程版)，2015，37(6)：730-734.

[2] 陈述,余迪,郑霞忠,等.重大突发事件的动态协同应急决策[J].中国安全科学学报，2015，25(3)：171-176.

[3] SUN B, MA W, ZHAO H. A fuzzy rough set approach to emergency material demand prediction over two universes [J]. Applied Mathematical Modeling, 2013,37(10):7062-7070.

[4] 刘北林,马婷.应急救灾物资紧急调度问题研究[J].哈尔滨商业大学学报(社会科学版)，2007(3)：3-6.

[5] 赵明,宋晓宇,董洁,等.利用遗传算法求解应急物资调度优化问题[J].沈阳建筑大学学报，2012，28(5)：944-948.

[6] 宋晓宇,刘春会,常春光.面向应急物资调度的一种灰色规划模型[J].计算机应用研究，2010，27(4)：1259-1262.

[7] ALEM D, CLARK A, MORENO A. Stochastic network models for logistics planning in disaster relief [J]. European Journal of Operational Research, 2016,255(16):87-206.

[8] HE Y X, LIU N. Methodology of emergency medical logistics for public health emergencies [J]. Transportation Research Part E: Logistics and Transportation Review, 2015,79(7):178-200.

[9] 马云峰,张敏,杨珺.物流设施选址问题中时间满意度函数的定义及应用[J].物流技术，2005，24(9)：26-29.

[10] 兰辉,何琴飞,边展,等.考虑道路通行状况的冷链物流配送路径优化[J].大连海事大学学报(自然科学版)，2015，41(4)：67-74.

[11] GAO W F, HUANG L L, WANG J,et al. Enhanced artificial bee colony algorithm through differential evolution[J]. Applied Soft Computing, 2016,48(11):137-150.

[12] EBRAHIMNEJAD A, TAVANA M, ALREZAAMIRI H. A novel artificial bee colony algorithm for shortest path problems with fuzzy arc weights [J]. Measurement, 2016,93(11):48-56.

[13] DWIVEDI A K, GHOSH S, NARENDRA D. Low power FIR filter design using modified multi-objective artificial beecolony algorithm [J]. Engineering Applications of Artificial Intelligence, 2016,55(10):58-69.

[14] 唐少虎,刘小明.一种改进的自适应步长的人工萤火虫算法[J].智能系统学报，2014，9(3)：265-275.

SUN Qiang:Lect.; School of Business Administration, Liaoning Technical University, Huludao 125105, China.

Location of Abrupt Disaster Emergency Logistics Center with Time Windows

SUNQiang

In order to maximize the improvement of emergency rescue time satisfaction, the location of abrupt disaster emergency logistics center with time windows restriction based on the rescue time and rescue satisfaction was built. Then the improved artificial bee colony algorithm was used for solving the model. The results show the improved artificial bee colony algorithm can effectively calculate the emergency logistics center location and relief supplies demand of different rescuer places. Compared with the model of abrupt disaster emergency logistics center location model without time window, this model satisfied the minimization of emergency rescue cost and maximization of rescue satisfaction at the same time.

abrupt disaster；location of abrupt disaster emergency logistics center；time windows ；rescue time satisfaction；improved artificial bee colony algorithm

2095-3852(2017)01-0001-05

A

2016-08-06.

孙强(1983-)，男，山东淄博人，辽宁工程技术大学工商管理学院讲师；博士.

X913.4

10.3963/j.issn.2095-3852.2017.01.001