基于混沌DESAPSO算法的无人机三维航迹规划

唐汇禹，彭世蕤，孙经蛟，刘香岚

(空军预警学院，武汉 430019)

【信息科学与控制工程】

基于混沌DESAPSO算法的无人机三维航迹规划

唐汇禹，彭世蕤，孙经蛟，刘香岚

(空军预警学院，武汉 430019)

粒子群(PSO)算法易陷入局部最优，将其运用于无人机三维航迹规划会导致航迹品质不高，针对这一问题，提出了将差分进化(DE)算法、模拟退火(SA)算法嵌入PSO算法中，构成混沌差分进化模拟退火粒子群(DESAPSO)算法，从三个方面提高了航迹品质：一是利用DE算法的变异、交叉及竞争选择增加种群多样性；二是利用SA算法概率突跳能力跳出局部最优解；三是对PSO算法参数进行混沌优化，进一步增强种群多样性。仿真结果表明：混沌DESAPSO算法改进航迹品质效果明显，获得了满意的无人机三维航迹。

混沌粒子群；差分进化；模拟退火；无人机；航迹规划

无人机航迹规划就是在满足威胁回避、机动性能限制等约束条件下，求得一条从起始点到目标点的最优或次优航迹，其实质为多目标优化问题[1]。而三维航迹规划搜索空间巨大，传统的经典算法诸如牛顿法、梯度法等已不适用，取而代之的是现代智能算法，其中具有代表性的包括粒子群算法(PSO)、遗传算法、蚁群算法和模拟退火算法等[2]。

PSO算法[3]具有实现容易、计算精度高、收敛速度快的特点，且其易与其他算法相结合，衍生出许多性能优良的算法。目前，已有许多学者将标准PSO算法及其改进算法运用于无人机航迹规划中，取得了许多成果[4-6]。但标准PSO算法后期易陷入局部最优，其根本原因是迭代后期粒子间相似度很高，种群多样性缺失。为了解决这一问题，提高航迹规划品质，在此从以下三方面来增加粒子种群多样性：一是利用差分进化算法的变异、交叉及竞争选择操作来增加种群多样性，其中变异和交叉算子采用非线性算子保证后期粒子若未能搜寻到全局最优解时，仍具有较高的全局搜索能力；二是利用模拟退火算法的突跳能力增加种群多样性，跳出局部最优找到全局最优；三是对PSO算法的参数采用混沌序列保证不重复遍历整个空间，进一步增强种群多样性。

将改进后的混沌DESAPSO算法运用于无人机三维航迹规划，通过与其他算法对比表明该算法性能优良。

1 无人机三维航迹规划建模

1.1 航迹编码

无人机航迹是由离散的导航节点直线相连而成的线路，算法中每个粒子的信息代表一条航迹。因此，可假设粒子数目为N，每条航迹除起始点和目标点外共有m个导航节点，整个种群可表示为：X=[X1,X2,…,XN]T，其中Xi为第i个粒子的位置。令Xi=[x0,xi1,…，xim,xt,y0,yi1，…，yim,yt,z0,zi1，…，zim,zt]，其中(x0,y0,z0)、(xt,yt,zt)为航迹起始点和目标点，(xim,yim,zim)为第i个粒子中第m个导航节点的三维坐标。

另外，考虑粒子位置虽可进行限制，但粒子运动是不定方向的、随机的，为确保粒子能从起始点朝着目标点方向运动，可采取对粒子x轴坐标进行固定均分，即将[x0,xt]均分成(m+1)段，y轴和z轴只做限制，不做均分。粒子在进行位置更新和限制时，只对y轴和z轴中除起始点和目标点外的m个导航节点进行操作。

1.2 航迹适应度函数

智能优化算法运用于航迹规划，需建立合适的适应度函数，适应度函数值即无人机飞行代价，该值是评价航迹优劣的唯一指标。无人机的适应度函数包括两大方面，分别为机动性能约束和威胁约束。其中，机动性能约束主要包括最大爬升角/下滑角、最大水平转弯角、最大航程、最小步长、最小转弯半径；威胁约束主要包括火力威胁、地形威胁和高度威胁。

对于机动性能约束代价，可参考文献[5]。其中最大爬升角/下滑角和最大水平转弯角代价函数表达式相同，最大航程代价和步长程度代价改进后分别如式(1)、式(2)所示。

(1)

其中，ltotal为总路程，L为起始点到目标点的直线距离，Lmax为无人机的最大航程。

(2)

其中，Lstep为步长程度标准值，Li为相邻节点的航迹长度。

而最小转弯半径约束，可通过爬升下滑角/水平转弯角、步长程度以及高度变化来合理控制，因此不对其另行约束，高度变化代价如式(3)所示：

(3)

其中，Δhi为相邻节点的高度变化值，CΔh为安全阈值。

威胁代价中的雷达威胁，可参考文献[7],导弹威胁和高炮威胁可参考文献[8]，对三种威胁进入禁飞区的情况，对式(1)施加惩罚K；地形威胁代价参考文献[8]，对进入禁飞区的情况同样施加惩罚K，另外将山峰地形等效成圆锥体存在一定误差，因此设置无人机飞行高度比当前地形高度高某一数值Clim，以此保证安全飞行，如式(4)所示：

(4)

其中，z(x,y)为无人机当前坐标的地形高度，z为无人机当前高度。

高度威胁可设置如式(5)所示的代价函数。

(5)

其中：z为当前飞行高度，Hmin为最小离地高度，Hmax为无人机以概率1被发现的高度。

综上，对任意航迹Xi，其航迹总代价如式(6)所示，通过设置不同的权值可以合理评价各代价对航迹的影响。

(6)

其中，N为粒子数；fk为各代价函数；M为代价种类数，ω1～ωM为相应的权值，其和值为1。

2 混沌DESAPSO算法

2.1DE算法

DE算法[9]包括变异、交叉以及竞争选择3步：首先，对第t代第i个粒子中的除开起始点和目标点外的y坐标和z坐标进行差分变异得到变异个体Ui(t+1)：

Ui(t+1)=Xr1,j(t)+F(Xr2,j(t)+Xr3,j(t))

(7)

其中，r1、r2、r3为[1,N]的随机整数，且满足r1≠r2≠r3≠i，j为除开起始点和目标点外的y坐标和z坐标，F为非线性变异算子，如式(8)所示：

(8)

其中，Fmax、Fmin分别为变异算子的最大值和最小值，T为最大迭代次数。

然后，对产生的变异个体进行交叉操作得到实验个体Vi, j(t+1)：

(9)

其中，CR为交叉率，采用如式(10)的非线性变异算子，randni为[m+3,2m+3]和[2m+6,3m+5]间的随机整数，m为前述导航节点数，这样做是保证实验个体Vi, j(t+1)至少有一位是由变异个体Ui, j(t+1)贡献。

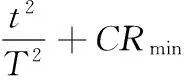
(10)

最后，对实验个体Vi(t+1)和种群个体Xi(t)进行竞争选择得到新一代种群个体Xi(t+1)：

(11)

2.2 混沌PSO算法

PSO算法起源于群鸟觅食，对于前述编码方式，可假设每个粒子速度为Vi=(vi1,vi2,…,viN)，粒子个体的最好位置为Pi=(pi1,pi2,…,piN)，其适应值称为个体极值，粒子群的最好位置为Pg=(pg1,pg2,…,pgN)，其适应值称为全局极值，粒子依据下式进行速度和位置更新：

(12)

(13)

其中，ω为[0,1]内的惯性因子，c1、c2称为学习因子，一般取2；r1、r2为[0,1]内变化的随机数，为确保不重复遍历整个搜索空间，可对参数r1、r2采取的混沌操作，混沌序列为logistic模型如式(14)。

(14)

2.3SA算法

SA算法[10]起源于固体退火过程，在采用了如式(15)所示的Metropolis准则后，算法具有以概率1收敛到全局极值的能力。

(15)

其中，Δf为后一代粒子适应值和前一代粒子适应值的差值，exp(-Δf/T(t))>rand项是为了保证前期温度较高时，即使后一代粒子适应值较差，仍具有以较高概率exp(-Δf/T(t))接受裂解的可能，从而跳出局部最优。后期随着温度降低，粒子接受裂解的可能变得极小，从而逐渐收敛到全局最优。要注意的是，后期虽然接受裂解概率极小，但不能排除有接受裂解的可能，因此应该实时保存迭代过程中找寻到的历史最优解。T(t)为当前迭代温度，温度衰减一般采用如式(16)的线性衰减，α为温度衰减系数，取值范围在[0.5,0.99]。

T(t)=α*T(t-1)

(16)

2.4 混沌DESAPSO算法流程

混沌DESAPSO算法是以PSO算法为主流程，主要过程包括三步：一是利用改进的DE算法对种群进行变异、交叉和竞争选择；二是利用混沌参数r1、r2对PSO种群进行再次遍历寻优；三是利用SA算法的Metropolis准则促使粒子群跳出局部最优，最终收敛到全局最优。

混沌DESAPSO算法具体步骤如下：

步骤1:初始化算法所有参数，包括粒子数N、最大迭代次数T、变异因子F、交叉因子CR、惯性权重ω、学习因子c1、c2、r1、r2、以及退火初始温度T0和温度衰减系数α，初始化种群位置和速度，且t=1；

步骤2:计算每个粒子的适应值，初始化个体极值pbest和全局极值gbest；

步骤3:迭代开始，按式(7)、式(9)和式(11)对初始化的粒子种群进行变异、交叉和竞争选择，更新个体极值pbest和全局极值gbest；

步骤4:按式(12)、式(13)对粒子进行速度和位置更新，进行速度和位置限制使其不超过边界，计算每个粒子适应值，进行个体极值和全局极值更新；

步骤5:计算前后代粒子的适应值差值Δf，按式(15)进行模拟退火操作，按式(16)进行降温操作；

步骤6:判断t是否小于等于最大迭代次数T，若是，转到步骤3；若否，算法结束，输出最优航迹。

3 仿真验证

本文特征地形模型参考文献[11]，模拟5座山峰，山峰中心坐标分别为(40,40)、(50,160)、(100,100)、(140,50)、(160,170)，山高Hi=[2.5,2.8,3.2,2.8,2.5]，无人机起点和终点分别为(10,10,2)、(130,110,3)，上述单位均为km。雷达威胁、导弹威胁以及高抛威胁参数如表1所示。

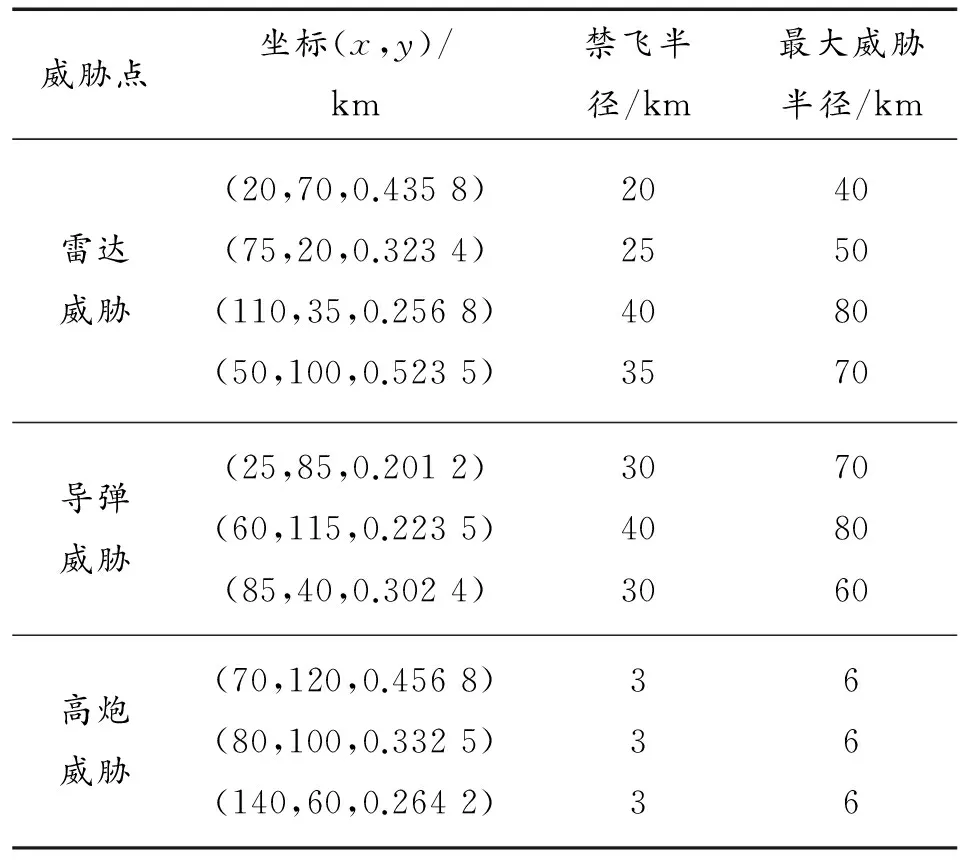
表1 威胁信息

分别用PSO算法、SAPSO算法以及混沌DESAPSO算法进行无人机三维航迹规划，各算法独立连续独立运行30次进行分析对比，混合算法参数同单一算法参数全部取相同，算法参数设置如下：PSO算法参数，粒子数目N=30，最大迭代次数T=500，惯性权重ω从0.9线性递减至0.2，学习因子c1=c2=2；SA算法参数，初始温度T0=4 000，温度衰减系数α=0.98；DE算法参数，变异因子F从0.7非线性递减至0.4，交叉因子从0.3非线性递增至0.8。各算法运行结果如表2所示。

表2 三种算法测试结果

从测试结果可以看出：PSO算法、SAPSO算法以及混沌DESAPSO三种算法收敛精度和稳定性依次不断提高，表明航迹规划品质不断提高；从数值变化来看，由于导航节点少、概率代价模型数值小以及对代价进行了1/13的加权平均，因此航迹品质改善明显；从平均时间来看，前两种算法复杂度相近，由于SAPSO算法收敛精度较PSO更高，因此平均耗时更短，而混沌DESAPSO复杂度明显高于前两种算法，以牺牲时间为代价获得了精度的提升。各算法迭代收敛曲线如图1(a)所示，局部放大如图1(b)所示。

由图1可知，混沌DESAPSO算法收敛速度最快，大约到10代就接近收敛到全局极值，PSO算法次之，SAPSO算法最慢。本文给出PSO算法和混沌DESAPSO算法二维及三维航迹对比图，分别如图2(a)、(b)和图3(a)、(b)。

由图2和图3可知：从二维航迹看，两种算法都能找到满足威胁回避、地形回避的可行航迹，且混沌DESAPSO算法能找到更加利用山峰遮蔽的二维航迹；从三维航迹看，混沌DESAPSO算法能找寻到高度更低、更靠近山峰飞行的三维航迹，也因此航迹品质更高，验证了航迹改善的有效性。

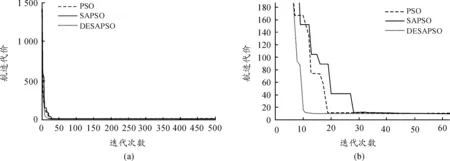
图1 三种算法迭代收敛曲线

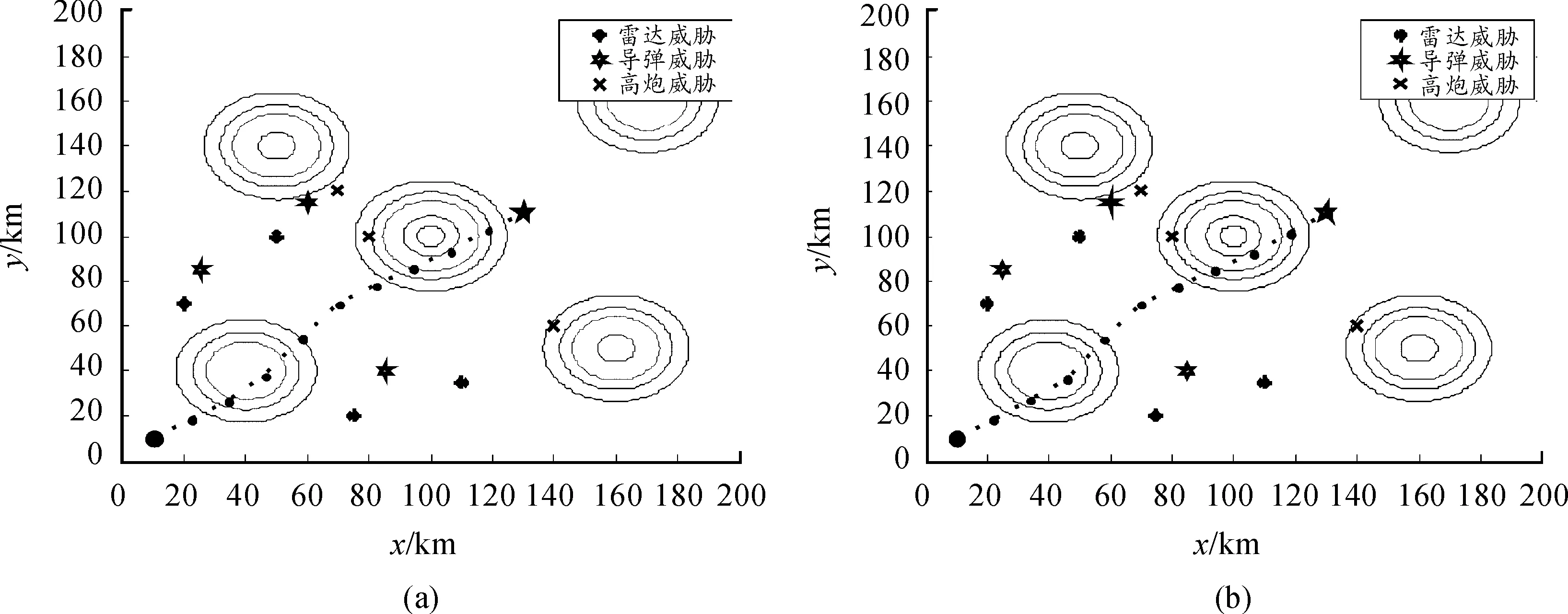
图2 PSO和混沌DESAPSO算法二维航迹

图3 PSO和混沌DESAPSO算法三维航迹

4 结论

本文针对将PSO算法运用于无人机三维航迹规划时易陷入局部最优，导致航迹规划品质不高的问题，提出将DE算法、SA算法嵌入到PSO算法中，并对PSO算法参数进行混沌优化以增加后期种群多样性，从而利用三种算法各自优点提高航迹规划品质。仿真结果表明：混沌DESAPSO算法对航迹品质改进效果明显，获得了满意的无人机三维航迹。

[1] 于成龙，刘莉，王祝,等.基于物理规划的无人机多目标航迹规划[J].电光与控制,2015,21(5):1-5.

[2] 王俊，周树道，朱国涛,等.无人机航迹规划常用算法[J].火力与指挥控制,2012,37(8):5-8.

[3] KENNEDY J，EBERHART R C.Particle Swarm Optimization[C]//Proceedings of the 1995 IEEE International Conference on Neural Networks,1995:1942-1948.

[4] 方胜良，余莉，汪亚夫.基于粒子群算法的无人机航迹规划[J].计算机仿真,2010,27(8):41-43.

[5] 陈琳，白振兴.应用PSO算法的无人机三维航迹规划[J].电光与控制,2008,15(4):50-53.

[6] 丁伟峰，汲万峰，严建钢，等.基于种群多样性测度的PSO算法及其应用研究[J].现代防御技术,2012,40(4):143-149.

[7] 王绪芝.不确定环境下无人机航迹动态规划及仿真研究[D].南京:南京航空航天大学,2013.

[8] 胡中华.基于智能优化算法的无人机航迹规划若干关键技术研究[D].南京:南京航空航天大学,2011.

[9] 刘建平.基于混沌和差分进化的混合粒子群优化算法[J].计算机仿真,2012,29(2):208-211.

[10]杨晓龙，曲东才.一种基于遗传模拟退火算法的航迹优化方法[J].四川兵工学报,2013,34(12):66-70.

[11]彭志红，孙琳，陈杰.基于改进差分进化算法的无人机在线低空突防航迹规划[J].北京科技大学学报,2012,34(1):96-101.

(责任编辑 杨继森)

3-D Route Planning of UAV Based on Chaotic DESAPSO Algorithm

TANG Hui-yu, PENG Shi-rui, SUN Jing-jiao, LIU Xiang-lan

(Air Force Early Warning Academy, Wuhan 430019，China)

Particle Swarm Optimization (PSO) algorithm is easy to fall into local optimum, and being applied to 3-D route planning of UAV will result in poor quality. To solve this problem, the chaotic DESAPSO algorithm was put forward by embedding the differential evolution (DE) algorithm and the simulated annealing (SA) algorithm in the chaotic PSO algorithm. The quality of the route was improved from three aspects, the first is to increase diversity of the population by using variation, crossover and competitive selection of DE algorithm; and the second is to jump local optimum by using the probabilistic jumping ability of SA algorithm; and the third is to increase diversity of the population further by chaotic optimization in the parameters of PSO algorithm. The results of simulation show that the quality of route was obvious improved by the chaotic DESAPSO algorithm, and the 3-D route was satisfied.

chaotic particle swarm optimization；differential evolution; simulated annealing; UAV； route planning

2016-08-14；

2016-09-20

唐汇禹(1991—)，男，硕士研究生，主要从事信息与通信工程研究。

10.11809/scbgxb2017.02.021

唐汇禹，彭世蕤，孙经蛟，等.基于混沌DESAPSO算法的无人机三维航迹规划[J].兵器装备工程学报，2017(2):92-96.

format:TANG Hui-yu, PENG Shi-rui, SUN Jing-jiao, et al.3-D Route Planning of UAV Based on Chaotic DESAPSO Algorithm[J].Journal of Ordnance Equipment Engineering,2017(2):92-96.

TP301.6

A

2096-2304(2017)02-0092-05