一种基于网格的等密度线聚类算法

徐明钊，杨 春，范 健，张 健，张耐民

(北京宇航系统工程研究所，北京 100076)

【信息科学与控制工程】

一种基于网格的等密度线聚类算法

徐明钊，杨 春，范 健，张 健，张耐民

(北京宇航系统工程研究所，北京 100076)

提出了一种基于网格的等密度线聚类算法，通过对样本所在空间进行网格划分，从样本分布等密度线图的思想出发，可自动发现任何形状的类，时间复杂度和空间复杂度较好，实现了对不同类样本空间容积的计算，具有很好的聚类效果和容积计算能力。

聚类；网格；等密度线；容积

聚类[1]作为数据挖掘中常用的手段，把一个没有类别标记的样本集在无先验知识的情况下按某种准则分成若干个子集，使相似的样本归为一类，而不相似的样本尽量划分到不同的类中。聚类分析的方法可以分为以下几类：基于划分的方法、基于层次的方法、基于密度的方法、基于网格的方法和基于模型的方法[2]。在实际应用中，常常需要针对不同算法的特点，结合上述多种聚类方法，才能针对具体问题收到理想的效果。本文提出了一种基于网格的等密度线聚类算法，实现了样本的聚类分析。

1 等密度线聚类算法

1.1 等密度线聚类算法概述

等密度线聚类算法是一种基于密度的聚类方法，密度是衡量点的疏密程度的概念。通常把每一样本作为中心，在一定体积内包含样本的数目作为该样本的密度。现有一些聚类算法(如DBSCAN算法等)只关注高密度样本的部分[3]，却忽视了高密度周围低密度数据集的聚类。另外，聚类过程中无法对孤立样本进行处理，所以不能对多密度数据集进行聚类。Chamelenon等一些算法尽管可以对多密度数据集进行聚类，但是聚类精度不高，无法对不同的密度区间进行准确划分。

赵艳厂等[4]从聚类点的样本分布等密度线图的思想出发，找出样本分布比较集中的区域，从而发现隐含在样本集中的类。在此基础上，本文提出了一种等密度线聚类方法，统计出每个样本邻域内包含样本的数目作为该样本的密度值，根据密度值实现对样本的聚类，其中每个子类可以是不连通的集合。

1.2 算法步骤

等密度线聚类算法的步骤如下：

1) 对于样本集中所有n个样本点X，统计出任意两点之间的距离，得到距离矩阵dist，dist(i,j)=D(X(i),X(j)),i,j=1,…,n。

2) 根据距离矩阵dist得到邻域大小RT，RT=mean(dist)/ncoefRT。其中mean(dist)是任意两点间的平均距离，coefRT是邻域调节系数，取值在0到1之间。实验发现coefRT取0.3时往往会有比较好的聚类结果。

3) 统计密度矩阵den即每个样本点在邻域RT内包含的样本点数目。密度矩阵den的统计示意图见图1，对于其中位于圆心处的点，在其RT邻域内的点的个数为4，那么该点的密度为4。

图1 密度矩阵den的统计示意图

4) 根据密度矩阵确定密度阈值向量DT，即密度线向量。DT的选择与样本的密度分布直接相关，例如当密度低到密度高的样本的个数呈现快速增长趋势，可将DT设定为一个等比增加的序列。具体使用过程中常常需要根据聚类的结果调整DT的取值，以便最后达到最满意的聚类效果。

5) 根据密度阈值向量DT完成子类的划分。把密度值在两条等密度线之间的样本归为一类。如果聚类效果不好，则调整DT的取值，重新聚类。

2 基于网格的等密度线聚类算法

2.1 基于网格的等密度线聚类算法概述

针对某些特定问题的聚类分析，除了完成已有数据样本的聚类外，还需要对聚类样本在空间内占据的空间大小或分布(容积)进行计算。等密度线聚类算法可以实现基于密度的聚类，但无法计算聚类样本的“容积”。为了解决这一问题，本文对该算法做了适当改进，提出了一种基于网格划分的等密度线聚类算法。

基于网格的聚类方法采用网格这一数据结构对聚类空间进行了划分，把空间量化为有限的数据单元，并以此为基本单位进行聚类[5]。经过网格划分后的空间聚类样本变成了网格，不再是孤立的样本点，因此方便了统计样本空间，实现了容积计算。

目前常见的基于网格的聚类算法有以下几种：STING算法是一种基于网格的多分辨率聚类方法，网格结构利于并行处理和数据的更新，效率高，但是聚类的精度较低；WaveCluster算法[6]在数据空间中加入了一个多维网格结构，并用小波变换变换原来的特征空间，算法较为复杂；CLIQUE算法[6]综合了基于密度和基于网格两种聚类算法，适合用于大型数据库和高位数据的聚类，但是聚类的精度较差。以上3种算法无法进行多密度聚类，也无法实现对聚类后容积的计算。

2.2 算法步骤

基于网格的等密度线聚类算法借鉴了基于网格的聚类算法以及等密度线聚类算法的思想，具体步骤为：

1) 对于样本集中所有n个样本点X，计算任意两点之间的平均距离mean(dist)，然后计算出邻域大小RT，RT=mean(dist)/ncoefRT，其中coefRT是邻域调节系数，计算过程同1.2节。

2) 网格的划分。把聚类空间每个维度划分为p个区间

表示上取整)

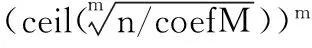
网格划分的大小将直接影响聚类的效果，网格太大或太小会导致网格中包含的样本数量不合理，导致最终的聚类结果不精确。此外如果网格太小，空间中网格数太多会导致时间复杂度大大增加。文献[7]给出了网格划分大小的依据，其中的区间划分系数coefM是一个正数的调节系数，其取值范围在一般情况下为1～2。

3) 邻域网格的确定。计算统计密度时，每一维的邻域网格数ri=ceil(RT/Leni×p)，其中，Leni是聚类空间在每一维上的长度投影。

步骤2)对聚类空间划分网格，但是统计密度的时候不宜直接统计每个网格中样本的个数，算法吸取了图像处理中的相关处理方法[8]，统计每个网格及其邻域中样本的数目，作为此网格的密度，相当于对网格密度做了一次高斯平滑，达到减少噪声的目的[9]。

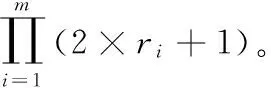
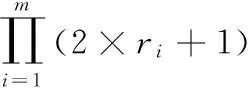
5) 根据网格密度矩阵确定密度阈值向量DT。算法密度阈值矩阵DT的确定仍然沿用等密度线聚类算法的公式。具体使用过程中常常需要根据聚类的结果调整DT的取值，以便达到最满意的聚类效果。

6)根据密度阈值向量DT完成子类的划分。把密度值在两条等密度线之间的样本点归为一类。如果聚类效果不好，则调整DT的取值，重新聚类。

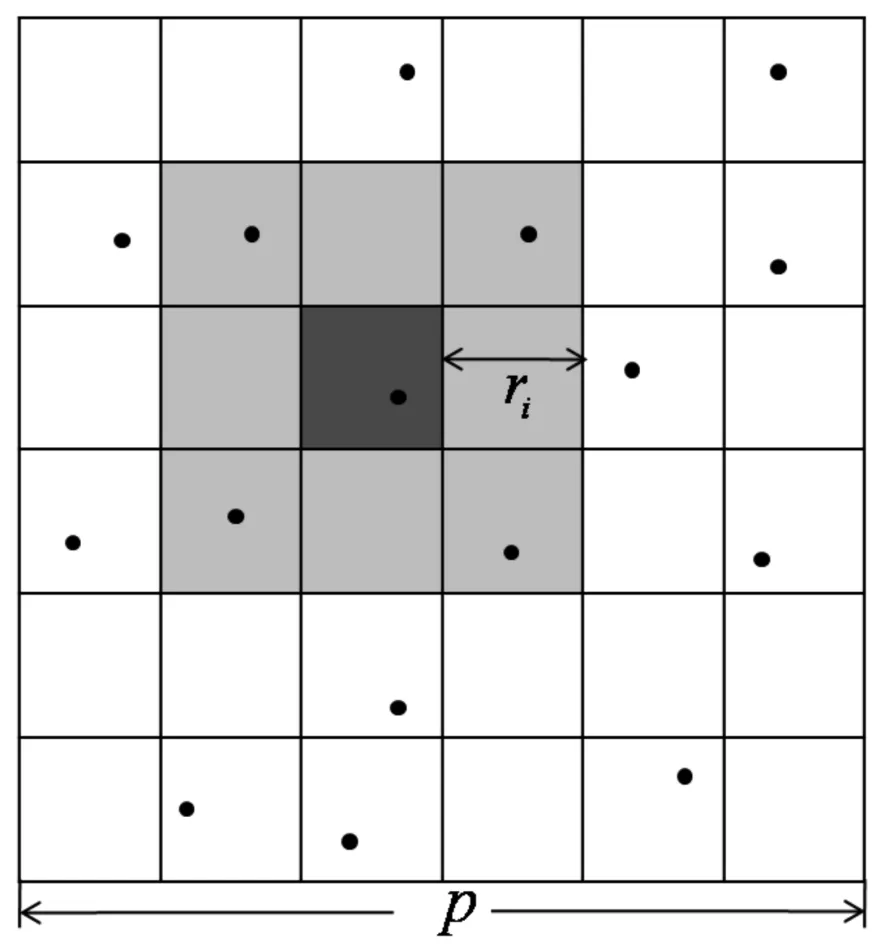
图2 密度矩阵den的统计

3 算法的性能分析

3.1 聚类结果比较

选取二维正态分布进行随机采样的点进行聚类，以对比基于网格的等密度线聚类算法与等密度线聚类算法的效果和性能。

二维正态分布的联合概率密度函数为

其中：μ1、μ2是两个变量的期望；σ1、σ2是两个变量的方差；ρ是协方差系数。

实验中二维正态分布的参数选取为

实验中设定聚类的子类数目为5。对于2 000点、6 000点的样本集，两种聚类方法得到的聚类结果如图3。

由图3所示的实验结果可以看出，基于网格的等密度线聚类方法与等密度线聚类方法具有相当的聚类效果。两种聚类方法都能够有效地将以二维正态分布采样的点聚类成5个近似同心圆环的子类，在样本点较多的情况下聚类效果更好。当样本点较少的情况下，两种聚类算法对子类边缘的样本不能很好的处理，聚类性能有所下降。

图3 两种聚类方法对不同样本点数的聚类效果比较

3.2 复杂度分析

在算例中，采用Matlab编程并利用Intel i7处理器的计算机计算，其中2 000点聚类计算中等密度线聚类算法耗时2.548 s，基于网格的等密度线聚类算法耗时1.782 s。

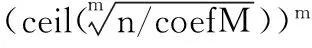
在基于网格的等密度线聚类算法步骤4)中提到，该算法密度矩阵可以由样本点更新的方式进行计算，这使得该算法具有良好的可更新性，适合在工程实践中使用。

3.3 容积的计算

基于网格的等密度线聚类算法由于对空间进行了网格的划分，在将样本聚类的同时也把整个空间分成了几个子类。因此，可以通过统计每个子类中网格的数目计算出每个子类的“容积”。图4给出了2 000个样本点时最终统计出的容积，不同深浅色表示了不同区域中子类的容积。如图4所示，对应于5个不同的子类，每个网格也被划分到相应的子类中，统计网格的面积就可以计算出每个子类容积的大小。经统计，按照密度从高到低的子类容积分别为15.87、51.21、43.46、38.73、250.73。

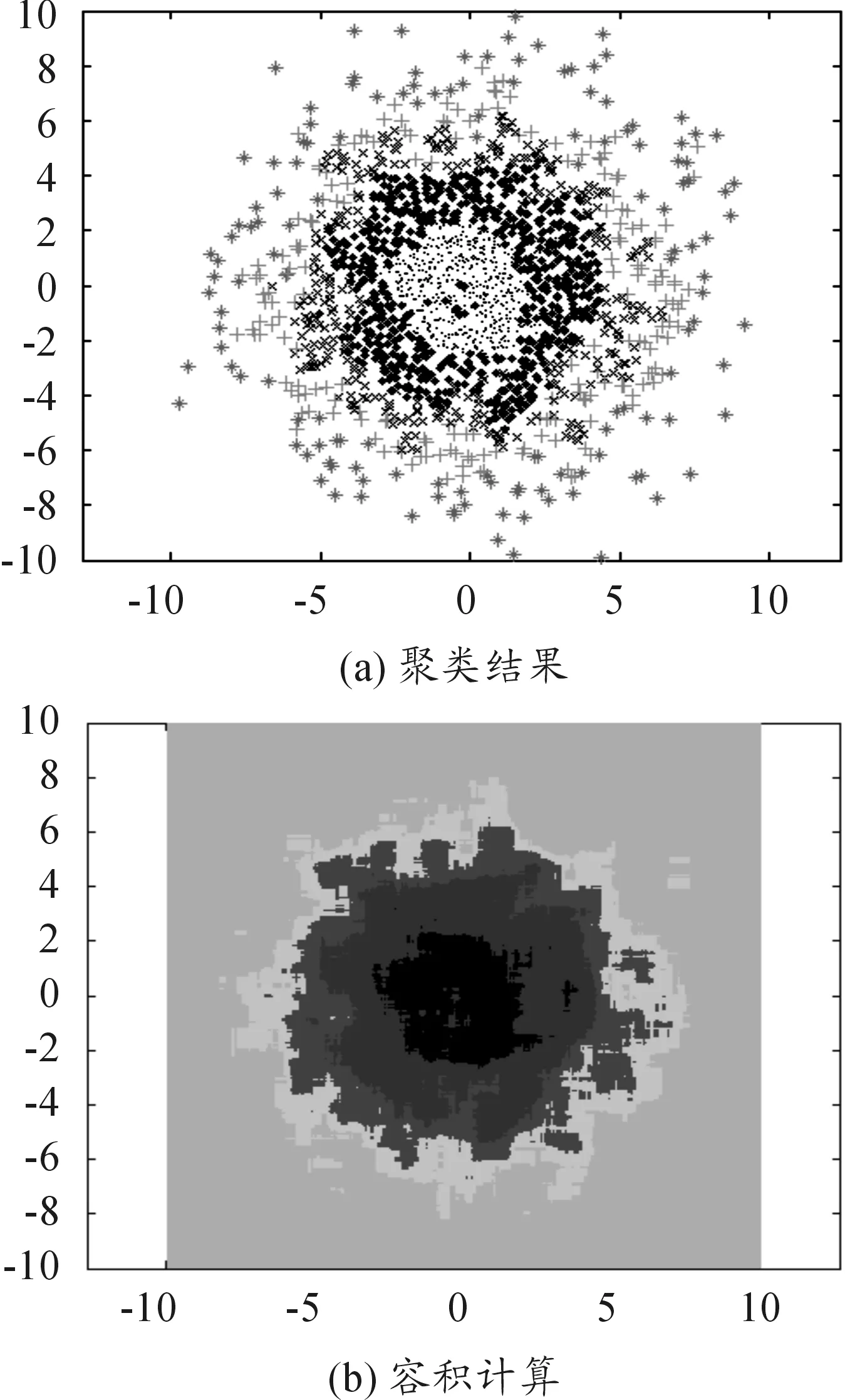
图4 基于网格的等密度线聚类方法容积的计算

4 结束语

基于网格的等密度线聚类算法步骤清楚，设计方法易于编程实现，时间复杂度和空间复杂度较好，可以完成对数据样本的有效聚类，同时实现了对样本空间容积的计算。该算法的提出可为数据挖掘的分析提供参考，具有较大的发展潜力。

[1] 廖芹,郝志峰,陈志宏.数据挖掘与数学建模[M].北京:国防工业出版社,2010.

[2] 吕晓玲,谢邦昌.数据挖掘方法与应用[M].北京:中国人民大学出版社,2009.

[3] 邱保志,沈钧毅.基于扩展和网格的多密度聚类算法[J].控制与决策,2006,21(9):1011-1014.

[4] 赵艳厂,谢帆,宋俊德.一种新的聚类算法:等密度线算法[J].北京邮电大学学报,2002,25(2):8-13.

[5] 张西芝.网格聚类算法的研究[D].郑州:郑州大学,2006.

[6] 赵慧,刘希玉,崔海青.网格聚类算法[J].计算机技术与发展,2010,20(9):83-89.

[7] GAO S,XIA Y.GDCIC:a grid-based density-confidence-interval clustering algorithm for multi-density dataset in large spatial database[C]//Proc of the 6 th International Conference on Intelligent Systems Design and Applications.Washington DC:IEEE Computer Society,2006:713-717.

[8] 田宇,罗辛.一种基于图像去噪的多密度网格聚类算法[J].智能计算机与研究,2014,6(1):45-47.

[9] 夏英,李克非,丰江帆.基于网格梯度的多密度聚类算法[J].计算机应用研究,2008,25(11):3278-3280.

[10]黄红伟,黄天民.基于网格相对密度差的扩展聚类算法[J].计算机应用研究,2014,31(6):1702-1705.

(责任编辑 杨继森)

A Grid-Based Density-Isoline Clustering Algorithm

XU Ming-zhao，YANG Chun，FAN Jian,ZHANG Jian,ZHANG Nai-min

(Beijing Institute of Aerospace System Engineering, Beijing 100076, China)

We proposed a grid-based density-isoline clustering algorithm. The algorithm meshes the space where the samples in, with the thought of density distribution, and it can automatically discover any kind of shape, and has great time complexity and space complexity. In addition, we achieved the calculation of the sample space of different types of volume. It has good clustering effect and volume grid-based computing capabilities.

clustering; grid-based; density-isoline; volume

2016-09-28；

2016-10-20

徐明钊(1986—)，男，硕士，工程师，主要从事导弹总体设计和智能算法研究。

10.11809/scbgxb2017.02.020

徐明钊，杨春，范健，等.一种基于网格的等密度线聚类算法[J].兵器装备工程学报，2017(2):88-91.

format:XU Ming-zhao，YANG Chun，FAN Jian, et al.A Grid-Based Density-Isoline Clustering Algorithm[J].Journal of Ordnance Equipment Engineering,2017(2):88-91.

TP181

A

2096-2304(2017)02-0088-04