内孔隔板脉冲固体火箭发动机隔板传热分析

李修明,王一白,李海涛，曹熙炜，刘 宇

(1.北京航空航天大学 宇航学院，北京 100191；2.上海航天技术研究院 806所,上海 201109；3.中国运载火箭技术研究院 研发中心，北京 100076)

【装备理论与装备技术】

内孔隔板脉冲固体火箭发动机隔板传热分析

李修明1,王一白1,李海涛2，曹熙炜3，刘 宇2

(1.北京航空航天大学 宇航学院，北京 100191；2.上海航天技术研究院 806所,上海 201109；3.中国运载火箭技术研究院 研发中心，北京 100076)

采用一维烧蚀模型和二维Ansys简化模型分别对内孔隔板脉冲固体火箭发动机的隔板热载荷进行了传热分析。结果表明，两种模型下隔板内侧温度随时间的变化规律基本一致，即在初期温度变化很小，基本稳定；经过一段时间，温度开始快速爬升；隔板越厚，温度爬升的时间点越靠后，温度爬升的速率越小。不同点在于，同样厚度的隔板，一维烧蚀模型温度爬升的速率比二维Ansys模型要大，即在同样的设计条件下，采用前者的隔板安全厚度要大于后者，可为工程应用提供一定参考。

脉冲固体火箭发动机；内孔隔板；传热；数值分析

脉冲固体火箭发动机不仅具有固体发动机结构简单、维护方便和安全性、可靠性高等特点[1-3]，相对普通固体发动机，它还具有比冲高(相对单室双推发动机)、射程远、拦截灵活、突防能力强和更好的推力矢量性能等优点，因而各国比较重视对它的研究[4-6]。脉冲固体火箭发动机的种类很多，常见的有喷射棒、铝膜隔板、硬隔板及软隔板[7]。内孔隔板脉冲固体火箭发动机如图1所示。目前国内对它的研究较少，但在国外它已经应用到“标准3”导弹上[8-9]。相对于其他隔板形式的发动机，内孔隔板既要承受过载产生的载荷，又要承受一级脉冲工作时的热载荷，对隔板的性能要求更高[10-11]。本研究针对隔板受到的热载荷，采用一维烧蚀模型和二维Ansys简化模型对隔板进行传热分析。

图1 内孔隔板脉冲发动机示意图

1 一维烧蚀模型

1.1 物理模型假设

热化学烧蚀模型目前广泛应用于烧蚀计算。北航的熊文波把它用于长时间端面燃烧发动机燃烧室的热防护分析[12]，计算结果和试验数据比较吻合。由于隔板所处热环境和端面燃烧发动机燃烧室绝热层类似，本研究采用热化学烧蚀模型对隔板进行热防护分析[13]。分析过程中作如下基本假设：

1) 所有化学反应发生在烧蚀表面上，因此可以直接由碳的质量消耗率折算为碳的线烧蚀率。表面上的凝相碳只与燃气外缘组分通过附面层扩散到壁面附近的氧化组分进行一级不可逆化学反应；

2) 热解气体的氧化组分和碳壁面进行一级不可逆化学反应；

3) 由于烧蚀引起计算区域的变化；

4) 计算过程中考虑由于热解而引起材料参数的变化；

5) 燃气沿内绝热层表面形成层流附面层；

6) 主流是冻结流，且附面层内各气体组元之间不发生化学反应，处于冻结状态；

7) 自由流中的Al2O3不进入附面层，既没有凝相沉积、粒子侵蚀，也没有粒子碰撞加热；

8) 认为内绝热层碳化层材料表面的强度足以承受表面摩擦力，即没有机械剥蚀；

9) 燃气及各气体组元是完全气体，服从Dalton定律；

10) 忽略附面层内的热传导，壁面附近气体分子运动的特征温度是碳壁温度；

11) 假设刘易斯数Le=1可得无量纲质量输运系数等于无量纲热输运系数，因此CM=CH；

12) 忽略体积力、Soret效应和Dofour效应，没有压强梯度扩散dP/dy=0；

13) Fick定律有效；

14) 不考虑喷管烧蚀对燃烧室压强的影响，即整个工作过程的总压一定，为发动机工作时间的平均压强；

15) 只考虑C和H2O、CO2以及OH三类型化学反应，即三方程热化学烧蚀模型。

为此可将燃烧室中的气体分为3类：

a)参加反应的组分：1-H2O，2-CO2，3-OH，4-CO，5-H2，6-H；

b)附面层内不参加反应组分：将其折算为等摩尔数，等效摩尔质量的7-gas1；

c)热解气体中不参加反应组分：将其折算为等摩尔数，等效摩尔质量的8-gas2。

如图2所示是隔板的烧蚀原理图。

图2 隔板烧蚀原理示意图

1.2 计算流程

1) 确定推进剂的配方，进行热力计算

对应于发动机不同推进剂配方和工作状况，可分别计算燃烧室的产物组分，同时可以得到相应的其他热力学参数，如定压比热容，比热比，特征速度等。

2) 进行不同内绝热层截面热化学烧蚀计算

利用热力计算的结果和材料参数以及发动机工作参数，采用三方程双控制机制模型可以计算不同截面的瞬时烧蚀率。这里，Fluent计算软件采用整场离散、整场求解的方法模拟燃气与固相材料间的非稳态流固耦合传热。不同内绝热层与燃气之间采用通用的控制方程，即

a)气相控制方程与湍流模型：

连续方程：

动量方程：

能量方程

组分扩散方程

▽

理想气体状态方程

湍流模型采用Realizablek-ε两方程模型，近壁处理采用增强型壁面函数。

b) 固相控制方程

固相材料瞬时导热方程

c) 气-固界面边界条件

质量平衡

组分平衡

能量平衡

d) 热化学反应速率

主要是C与燃气氧化性组分H2O、CO2、OH反应生成CO，烧蚀反应方程式及其动力参数见表1。

反应速率根据Arrhenius定律计算，由反应所致的壁面退移速率即为烧蚀率

3) 不同时刻一维温度场计算

利用计算得到的瞬时烧蚀率，对内边界移动处理。进行一维温度场计算，获得壁面温度和热解气体流量。

4) 烧蚀和传热的耦合

利用温度场计算得到的壁面温度和热解气体流量，代入到烧蚀程序中进行烧蚀计算，同时利用烧蚀计算得到的烧蚀量和内边界净热流密度代入到温度场计算中计算温度分布，实现烧蚀和传热计算的间接耦合。

表1 烧蚀反应方程式及其动力参数

1.3 计算结果

图3是不同厚度隔板内侧温度随时间变化曲线，可以看出，不同厚度隔板的内侧温度随时间变化规律是一致的：① 在初期，温度变化很小，基本稳定在初始温度水平；② 经过一段时间，温度开始快速爬升；③隔板越厚，温度爬升的时间点越靠后，温度爬升的速率越小。在工程应用中，可以根据一级脉冲的工作时间选择合适的隔板厚度。

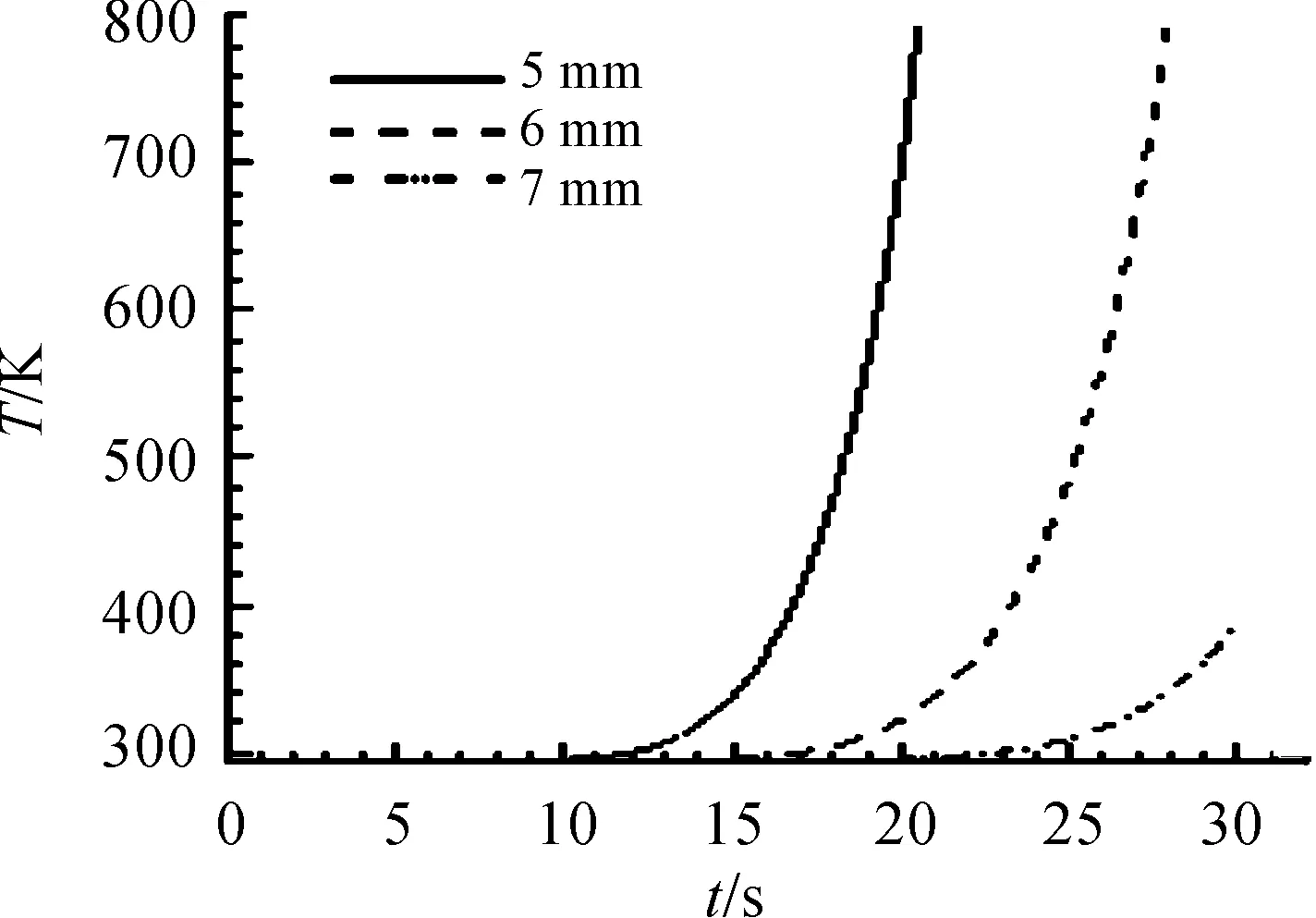
图3 不同隔板厚度内侧温度随时间变化曲线

图4是隔板厚度为7 mm时的内外侧温度随时间变化曲线。可以看出，隔板外侧的温度在很短的时间内达到了燃气的温度，并逐渐趋于平稳；而内侧的温度在开始的一段时间内变化很小，只是到了某一时间点才开始迅速爬升。这主要是因为隔板外侧和燃气直接接触，通过辐射、热传导和对流使得温度迅速上升；而热流通过隔板向里传播的过程中，大部分的热流被隔板吸收用于材料的热解、碳化等，传到内侧的热流很少，但随着材料热解程度的加大和烧蚀的产生，越来越多的热流开始传到隔板内侧，使内侧温度迅速爬升。

图4 隔板内外侧温度随时间变化曲线

2 Ansys二维计算

2.1 物理模型

上述烧蚀计算是不考虑轴向作用的一维计算，下面利用Ansys软件进行二维温度场计算。在模拟过程中不考虑烧蚀，隔板厚度为7 mm。计算物理模型如图5所示。

图5 Ansys计算模型

2.2 Ansys计算结果分析

图6、图7是隔板厚度为7 mm时的温度云图及特征点随时间的变化曲线。从不同隔板厚度的云图和曲线来看，温度随时间的变化规律跟一维烧蚀模型是一致的，在初期，温度变化很小，随后有一个温度爬升段。

图6 隔板厚度为7 mm时的温度云图

图7 隔板厚度为7 mm时特征点处温度随时间变化曲线

3 一维烧蚀计算和Ansys二维计算比较

图8中有两种传热计算模型的对比曲线，从中可以发现，两种模型的规律基本一致。初期，两者的温度变化都很小，随后有一个温度爬升段，烧蚀模型的温度爬升速率要高于不考虑烧蚀的模型。这主要因为，在开始的一段时间，隔板的温度比较低，隔板材料的热解、碳化及烧蚀需要一定的时间，而当材料出现烧蚀后，隔板内侧的温度自然就快速爬升了。

图8 烧蚀模型和Ansys简化模型比较

4 结论

1) 在一维烧蚀计算中，隔板内侧温度随时间的变化规律：① 初期温度变化很小，基本稳定在初始温度水平；② 经过一段时间，温度开始快速爬升；③ 隔板越厚，温度爬升的时间点越靠后，温度爬升的速率越小；

2) 在Ansys二维简化模型计算中，隔板内侧温度随时间的变化规律跟一维烧蚀计算是相同的；

3) 通过比较一维烧蚀计算结果和Ansys二维简化模型计算结果得出，在同样的隔板厚度下，前者的温度上升速度大于后者，即在同样的设计条件下，采用前者时的隔板安全厚度要大于后者，这给工程应用提供一定参考。

[1] NAUMANN K W，STADLER L，TROUILLOT P，et al.Double-Pulse Solid Rocket Technology At Bayern-Chemie/Protac[R].AIAA2006-4761.

[2] STADLER L J，TROUILLOT P，RIENCKER C， et al.The Dual Pulse Motor For LFK NG[R].AIAA2006-4726.

[3] TROUILLOT P，AUDRI D，RUIZ S， et al.Design of internal thermal insulation and structures for the LFK-NG double-pulse motor[R].AIAA2006-4763.

[4] 叶定友，王敬超.固体发动机多次起动技术及其应用[J].推进技术，1989(4):32-34.

[5] 阮崇智.战术导弹固体发动机的关键技术问题[J].固体火箭技术，2002， 25(2):8-12.

[6] SCHILLING S，TROUILLOT P.On the Development and Testing of a 120mm Caliber Double Pulse Motor(DPM)[R].AIAA 2004-3387.

[7] 王春光,刘洪超,杨德敏.脉冲发动机隔离装置发展现状研究[J].航空兵器,2012,10(5):48-51,60.

[8] 刘延国，何洪庆.多脉冲控制在战术导弹中的作用[J].推进技术， 1998(5):110-114.

[9] TROUILLOT P,AUDRI D,RUIZ S.Design of internal thermal insulation and structures for the LFK-NG double-pulse motor[R].AIAA2006-4763.

[10]石瑞,王长辉，苌艳楠.双脉冲固体发动机铝膜隔板设计和试验研究[J].固体火箭技术,2013,36(2):190-194.

[11]曹熙炜,任军学,王长辉,等.软隔板双脉冲发动机二级点火延迟试验分析[J].北京航空航天大学学报,2012,38(2):244-246.

[12]熊文波,刘宇,任军学,等.小推力长时间工作固体火箭发动机初步试验研究[J].固体火箭技术,2009,32(4):413-417.

[13]王春光,田维平,任全彬,等.脉冲发动机中隔层工作过程的数值分析及试验[J].推进技术2012,33(5):791-794,830.

(责任编辑 周江川)

Analysis on Clapboard Heat Transfer of Inner Bore Clapboard Dual-Pulse Solid Rocket Motor

LI Xiu-ming1, WANG Yi-bai1, LI Hai-tao2, CAO Xi-wei3, LIU Yu2

(1.School of Astronautics, Beihang University, Beijing 100191, China;2.806 Institute Shanghai Academy of Spaceflight Technology, Shanghai 201109, China;3.Research of Development Center, China Academy of Launch Vehicle Technology, Beijing 100076, China)

The analysis on inner bore clapboard dual-pulse solid rocket motor was carried out using the one-dimension ablation model and two-dimension Ansys model. The results show that the law of the inside temperature of clapboard varying by time is consistent under the two models. At beginning, the temperature does not vary much and retains constant. After a while time, the temperature starts to climb quickly. When the clapboard is thicker, the time of the temperature climbing comes later and the velocity of the temperature climbing is smaller. The main difference of the two models is that the velocity of the temperature climbing of the former is larger than the latter one, which can provide reference for engineering application.

dual-pulse solid rocket motor; inner bore clapboard; heat transfer; numerical simulation

2016-09-27；

2016-10-25

上海航天科技创新基金资助项目

李修明(1990—),女,硕士，主要从事固体火箭发动机方面研究。

10.11809/scbgxb2017.02.014

李修明,王一白,李海涛，等.内孔隔板脉冲固体火箭发动机隔板传热分析[J].兵器装备工程学报，2017(2):57-60.

format:LI Xiu-ming, WANG Yi-bai, LI Hai-tao,et al.Analysis on Clapboard Heat Transfer of Inner Bore Clapboard Dual-Pulse Solid Rocket Motor[J].Journal of Ordnance Equipment Engineering,2017(2):57-60.

V435.23

A

2096-2304(2017)02-0057-04