水听器阵列定位中的时延估计方法研究

邵宗战，张 虹，杨大伟

(中国人民解放军91439部队， 辽宁 大连 116041)

【装备理论与装备技术】

水听器阵列定位中的时延估计方法研究

邵宗战，张 虹，杨大伟

(中国人民解放军91439部队， 辽宁 大连 116041)

针对水下定位过程中时延估计计算量大，难以实时实现的问题，提出了一种适用于水听器阵列水下定位系统的互相关时延估计方法；该方法根据瞬时相干函数的计算结果确定是否更新时延估计值，根据水听器阵列拓扑结构限定最大时延范围减少互相关函数的运算次数，降低了时延估计的计算复杂度；仿真分析验证了所提方法的有效性。

时延估计；水听器阵列；广义互相关；CSP；相干函数

在水中兵器试验中，水下航行时的位置、速度等运动信息是分析判断水中兵器战术技术性能的重要信息，也是检验和鉴定水下武器作战性能的依据。水下定位技术利用分布于不同位置的水听器阵列接收水声信号，确定水下目标的方位、距离、速度等，在军事对抗、海洋资源利用和水下机器人探测等领域应用非常广泛[1]。利用单个矢量水听器也能够进行水下目标定位，但由于单水听器只能利用时频信息，在强混响环境下定位精度较低，而且容易定位出虚假目标。利用多个水听器组成的传感器阵列所提供的空域和时频域信息，能够很好地解决这一问题[2]。国内外对于水听器阵列水下定位的研究已经比较成熟，提出了大量有效的解决方法。

对于大部分水听器阵列定位方法，时延估计是实现远距离水下被动定位的重要手段，其准确性直接关系水下定位的精度。在实际应用中，受海域深度限制，混响现象无法避免，各水听器接收信号的干扰彼此之间也存在较强的相关性，而且水下目标的位置一般随时间发生变化，这些因素都导致时间延迟估计精度难以满足实际需求。

通过某种最优准则下的自适应滤波，能够自动调节滤波器自身结构以实现参数的最优化处理，同时给出时延估计值[3]，但这类方法对参数结构的初始化比较困难；而且，对于海底反射形成的多路混响信号，用其中一路信号简单地通过时间平移去近似另外一路信号从而得到两者的关系也比较困难[4]。

互功率谱相位(CSP)[5-6]方法和广义互功率谱相位(GCSP)方法在信噪比较高时均能得到较为准确的时延估计结果，但其性能与信号帧长关联性较强，只有长帧信号才能得到理想的估计结果。而长帧信号的处理计算量大，在水听器路数较多时，处理每帧信息所需时间较长，难以保障系统对信号的实时处理。

本文采用瞬时相干函数互相关原理，提出了一种满足水听器阵列拓扑结构实时进行时延估计的方法。该方法能够根据瞬时相干函数的计算结果确定是否更新时延估计值，降低了时延估计算法的复杂度，实现多路水声信号在定位系统中的实时处理。

1 互相关时延估计方法

通过互相关进行时间延迟估计是一种常用的时延估计方法[7-8]。该方法使用不同水听器所拾取的水声信号之间的互相关函数，比较不同信号之间的相似程度，当互相关函数的自变量取值等于所拾取信号的时间延迟时，该函数的值达到最大。此时，只需计算出互相关函数的峰值所对应的时间值，就可以计算出这两路信号的时延估计值。

1.1 互相关方法

如果不考虑水声信号经多径反射后产生的多径干扰，只考虑水听器阵列的背景噪声，则水听器阵列中第i个水听器接收到的信号xi(t)可以表示为

xi(t)=αis(t-τi)+ni(t) (i=1,2,…,M)

(1)

式(1)中s(t)为水下声源信号，ni(t)表示第i个水听器所接收的噪声信号，任意两路信号xi(n)和xj(n)之间的互相关函数表示为

Rij(τ)=Rss(τ-Dij)+Rsni(τ-Dij)+

Rsnj(τ)+Rninj(τ)

(2)

其中Dij表示水听器i与水听器j之间的时间延迟。假定s(t)、ni(t)和nj(t)之间两两独立，即式(2)的后面3项全部近似为零，则式(2)简化为信号s(t)的自相关函数：

Rij(τ)=Rss(τ-Dij)

(3)

对自相关函数Rij(τ)，当自变量τ=Dij时，Rss(τ-Dij)取最大值，τ值即认为是时间延迟的估计值。

1.2 广义互相关方法(GCSP)[9]

互相关方法假定水下声源与环境噪声之间、噪声与噪声之间互不相关，该条件在一般情况下难以满足；而且，在实际应用中，只能用有限时间内的函数的平均值逼近相关函数中的期望统计平均，这导致互相关方法对时间延迟估计的精度较低。为了锐化互相关函数，降低这两种因素对互相关时延估计结果的影响，人们研究出各种不同的加权方法对互相关函数进行加权处理，并将这类时延估计方法统称为广义互相关法，其实质是先将互相关函数变换到频域内加权，然后再反变换至时域的一种处理方法。

两水听器所接收信号的广义互相关函数定义如下

(4)

其中Xi(ω)和Xj(ω)分别表示水听器接收信号xi(n)和xj(n) 在频域的离散傅里叶变换，ψij(ω)是广义加权函数。对不同的使用条件，加权函数ψij(ω)可以选择不同形式，以使互相关函数Rij(τ)锐化，易于分辨。当ψij(ω)=1时，该方法退化为基本的互相关方法。

1.2.1 互功率谱相位(CSP)方法

式(4)中的加权函数ψij(ω)有多种不同的表示形式，代表了不同的广义互相关方法，较为常用的加权函数形式为

(5)

其中Gxixj(ω)为两路水声信号的互功率谱函数，式(5)所表示的时延估计方法称为互功率谱相位(CSP)时延估计方法。

在实际应用中，既要考虑信号模型中的干扰噪声niI(t)，又不能忽略混响噪声niR(t)，此时两个水听器接收到的信号xi(t)和xj(t)的互功率谱函数Gij(ω)表示为

(6)

其中

Ni(ω)=NiI(ω)+NiR(ω)

(7)

NiI(ω)和NiR(ω)分别表示niI(t)和niR(t)的傅里叶变换函数。将式(7)代入式(6)，假定水声信号s(t)与环境噪声niI(t) 和njI(t)之间互不相关，则式(6)可以简化为以下形式

(8)

弱混响条件下，后3项全部近似为零，则互功率谱函数Gij(ω)可以进一步简化为

αiαjS(ω)S*(ω)e-jω(τi-τj)

(9)

式(9)与理想条件下得到的计算结果相近，说明互功率谱相位时延估计方法虽然是针对理想条件提出来的，但在信噪比较高时，时延估计结果仍准确。在信噪比低、混响严重的环境中，式(8)的后面3项不能忽略，此时采用式(9)计算互功率谱函数将导致CSP时延估计性能下降。

1.2.2 改进的互功率谱相位(GCSP)方法

为了提高CSP方法的时延估计精度，锐化互相关函数在时域内的峰值，直接用水声信号的功率谱函数获得加权函数，即令

(10)

可以获得更为准确的时延估计值，这就是GCSP方法。该方法在本质上是将|S(ω)|2作为水听器接收信号互功率谱函数Gij(ω)取平均值后的结果，即

(11)

由式(11)可知，在GCSP方法中，使用的水听器数目越多，所求得的|S(ω)|2越接近其真实值，对应算法的性能越优越。

1.2.3 互功率谱相位方法仿真分析

为比较CSP方法和GCSP方法的性能，对上述两种方法进行仿真测试。仿真实验在5 km×4 km的矩形空间内进行，使用两段含噪水声数据作为原始的输入信号，两组水听器接收到的水声信号用IMAGE模型[10]仿真获得。仿真时低混响信号的采样率设定为1.1 kHz，混响时间为3 s；高混响信号采样率设定为2.5 kHz，混响时间为0.6 s。传感器阵列由4个水听器构成，它们分别位于半径为1.2 km的圆的两个互相正交的直径端点上，形成均匀圆形阵列，圆心位于(1,2) km处，声源坐标为(2.5,2)km。对已知时延的两路信号，分别用CSP法和GCSP法计算90帧长度信号的时延估计，得到图1和图2所示的测试结果。

图1 帧长和混响不同时CSP方法的时延估计性能

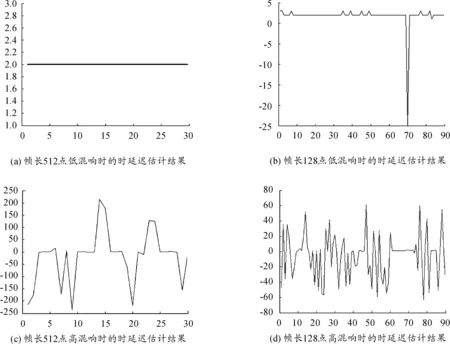
图2 帧长和混响不同时GCSP方法的时延估计性能

由图1和图2的仿真结果可以看出，当帧长缩短时，CSP方法和GCSP方法的时延估计性能均有所下降。在低混响条件下，两种方法都能给出了相对准确的时延估计结果，但 GCSP的性能优于CSP；随着混响的增强，两种方法时延估计的精度急剧下降，尤其当帧长较短时，估计结果呈现剧烈振荡，此时，CSP法和GCSP法的性能没有明显的差异。

在工程应用中，如果希望CSP及其改进方法获得可靠的时延估计结果，需要选取较长的信息帧。然而对于M路水听器构成的定位系统，每次时延估计需要做M(M-1)次FFT及IFFT运算，帧长加大导致计算量大幅增加，当M较大时，系统实时实现的成本急剧增加。此外，互功率谱函数方法还需要预估水声信号的功率谱密度函数以求得加权函数，这要求估计过程中的每帧信号都包含实际的水声信号，保证时延估计结果相对准确，因此，在时延估计过程中还需要同步完成信号强度检测，这进一步增加了该方法的计算复杂度。

2 基于瞬时相干函数的互相关方法

为在时延估计的准确性与计算复杂性之间取得平衡，利用水听器阵列拓扑结构的特点，根据瞬时相干函数的计算结果确定是否更新时延估计值，不仅能够得到满意的时延估计结果，而且还可以有效降低计算复杂度，适用于水听器阵列水下定位的实时处理系统。

2.1 瞬时相干函数互相关方法[7]

由式(3)可知，当互相关函数取最大值时，对应的时间就是所需的时延估计值，互相关函数的最大值可以认为是无噪声水声信号s(t)的平均功率。为了区分高/低信噪比条件，以确定是否更新时延值，定义瞬时相干函数：

(12)

式(12)中Rii(0)和Rjj(0)表示含噪声信号的平均功率，它满足以下条件：

Rii(0)=Rjj(0)=Rss(0)+Rnn(0)

(13)

当τ=Dij时，由式(12)和式(13)可知

(14)

γxixj(Dij)是瞬时相干函数γxixj(τ)的最大值，可用于判定是否存在水声信号[6]。由于其大小与信噪比相关，因此还可以通过式(14)检测信噪比的高低。当信噪比较高时，γxixj(Dij)接近1；信噪比较低时，γxixj(Dij)的值接近于0。据此，设定某一门限值，当信息帧的γxixj(Dij)值高于门限时，才进行时延估计。这样，利用高信噪比信息帧进行时延估计，忽略低信噪比信息，不仅能够获得相对准确的时延估计结果，还能够降低噪声干扰对时延估计结果的影响。

2.2 仿真分析

进行时延估计时，信息帧长为128，根据水声信号的特点，设定相干检测时的门限值为0.8，若相干函数的峰值大于0.8，认为当前时刻水声信号信噪比较高，更新此时的时延估计值；若峰值小于0.8，继续沿用上一时刻的时延估计值，不更新延估计更新值。仿真得到如图3所示的时延估计及相干函数随时间变化的趋势图。

由图3可以看出，水声信号信噪比较低时，如果不经过相干检测处理，时延估计的结果振荡明显；选择适当的门限进行相干检测，则时延估计值均匀地控制在真实值附近，能有效地减小误差。

对比分析图1、图2和图3可见，对于低混响信号，相干函数互相关法的时延估计结果与帧长相同的CSP法和GCSP法结果相近，估计误差都在允许范围之内；对于高混响信号，相干函数互相关法的时延估计结果明显优于帧长相同时的CSP法和GCSP法对应的估计结果，该方法不仅避免了时延估计值的振荡，而且时延估计时所用帧长较短，降低了计算复杂度，适用于水听器阵列水下实时定位系统。

2.3 时延估计方案设计

试验中，水听器阵列的形状、阵元的个数以及阵元的间距都是确定的。因此，各阵元之间的最大时延值可以根据采样率以及阵列结构预先确定。应用相关方法进行时延估计时，将参与运算的两组输入信号的互相关值限定在最大理论时延值之内，在此范围内搜索峰值，而不在帧长范围内搜索峰值，能够降低计算复杂度。在图4所示的均匀圆形水听器阵列中，实线表示水听器接收到的直达信号，虚线为两路水听器之间的最大路径差dn(n=1,2,…,M/2)，假定采样率为fs，声音在水下的传播速度为vs，则相对于基准水听器，第n路水听器的最大时延τn为

(15)

式中dn可由余弦定理计算求得。这样，在时延估计过程中，先根据阵列结构计算各水听器接收到的水声信号相对于基准水听器的最大时延值，不仅可以缩小峰值搜索范围，还可以将最大时延值作为时延估计时的初值。

图3 时延估计及相干函数随时间变化

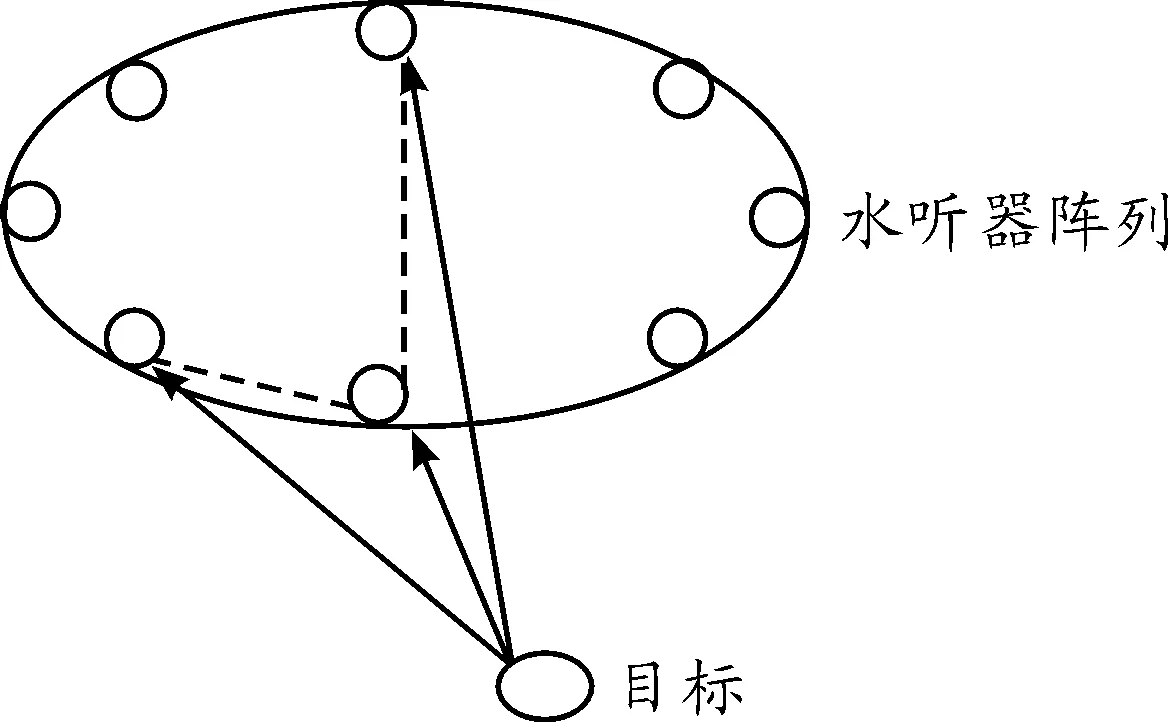
图4 均匀圆形水听器阵列拓扑结构

对于运动目标，各水听器所处位置相对于声源不断变化，如果不实时更新信号到达不同水听器的延迟估计值，会影响水下定位精度。本文的水听器阵列定位系统通过相干函数检测控制时延估计结果更新。当信噪比高于设定的门限时，进行时延估计值更新；反之继续使用上一帧得到的时延估计值，降低实时监控的难度。

图5给出了应用于水听器阵列水下实时定位系统时延估计方法的实现流程。

图5 水听器阵列定位系统实现流程

该方法对各水听器接收的水声信号重叠加窗预处理后，检测基准水听器接收信号的强度，如果信噪比超过设定的门限值，判决该帧水声信号为信息帧，并计算时延值。之后计算瞬时相干函数，如果相干函数的峰值大于设定门限，更新时延估计值并利用该时延估计结果定位水下目标；否则，不更新时延估计值，也不更新水下目标位置。

3 结论

本文针对水听器阵列定位过程中时延估计计算复杂度高，难以实时更新问题，利用相干函数检测确定延估计的时机，根据水听器阵列的拓扑结构限定峰值搜索范围，在计算复杂度和估计性能之间取得了较好的均衡，解决了水听器数目较多、帧长较长时的水下目标实时定位问题。

[1] 焦小涛.水下目标被动定位系统关键技术研究[D].西安:西安工业大学,2013.

[2] EHUD Weinstein.Optimal Source Localization and Tracking from Passive Array Measurements[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1982,30(1):69-76.

[3] YOUN D,AHMED N,CARTER C.On Using the LMS Algorithm for Time Delay Estimation[J].IEEE Transaction on Acoustics,Speech and Signal Processing,1982,30(5):798-801.

[4] STEVEN K.Fundamentals of Statistical Signal Processing,Estimation Theory[M].Englewood Cliffs,New Jersey:Prentice-Hall,1993.

[5] OMOLOGO M,SVAIZER P.Acoustic Event Localization Using a Crosspower Spectrum Phase Based Technique[C]//Adelaide,1994,ICASSP:273-276.

[6] OMOLOGO M,SVAIZER P.Use of the Crosspower-Spectrum Phase in Acoustic Event lLocation[J].IEEE Transactions on Speech and Audio Processing,1997,5(3):288-292.

[7] 王宏禹，邱天爽.自适应噪声抵销和时间延迟估计[M].大连：大连理工大学出版社，1999.

[8] 火久元，刘立群，赵红星.基于混合蛙跳算法的水文模型参数估计方法[J].重庆理工大学学报(自然科学),2016(3):80-86.

[9] KNAPP C,CARTER C.The Generalized Correlation Method for Estimation of Time Delay[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1976,24(4):320-327.

[10]ALLEN J，BERKLEY D.Image Method for Efficiently Simulating Small-room Acoustics[J].Journal of the Acoustical Society of America.1979,65(4):943-950.

[11]金磊磊，马艳.水听器阵列定位中的时延估计方法研究[J].探测与控制学报，2015(2):90-94.

(责任编辑 周江川)

Research on Time Delay Estimation Methods in Underwater Hydrophone Array Localization

SHAO Zong-zhan, ZHANG Hong, YANG Da-wei

(The No. 91439thTroop of PLA, Dalian 116041, China)

A real-time time delay estimation method using correlation function based on coherence function was provided to mitigate the large computational complexity problem. This method can not only give out more exact TDE result in case of strong reverberations and low Signal-to-Noise Ratio (SNR), but also reduce the complexity of correlation function when the maximal value of time delay is established according to topology structure of the hydrophone array. Simulation results show the validity of the proposed method.

time delay estimation; hydrophone array; generalized correlation function; CSP; coherence function

2016-09-25；

2016-10-31

邵宗战(1972—)，男，高级工程师，主要从事试验总体技术研究。

10.11809/scbgxb2017.02.008

邵宗战，张虹，杨大伟.水听器阵列定位中的时延估计方法研究[J].兵器装备工程学报，2017(2):30-35.

format:SHAO Zong-zhan, ZHANG Hong, YANG Da-wei.Research on Time Delay Estimation Methods in Underwater Hydrophone Array Localization[J].Journal of Ordnance Equipment Engineering,2017(2):30-35.

TN911

A

2096-2304(2017)02-0030-06