活性粉末混凝土单轴受压应力—应变关系研究综述★

曾 翔 邹 娟 曹宝珠

(1.海南大学土木建筑工程学院,海南 海口 570228； 2.海南国际旅游岛发展研究院,海南 海口 570228； 3.海南工商职业学院，海南 海口 570203)

活性粉末混凝土单轴受压应力—应变关系研究综述★

曾 翔1,2邹 娟3曹宝珠1

(1.海南大学土木建筑工程学院,海南 海口 570228； 2.海南国际旅游岛发展研究院,海南 海口 570228； 3.海南工商职业学院，海南 海口 570203)

介绍了活性粉末混凝土(RPC)所具有的优点，结合RPC单轴受压应力—应变关系的研究现状，分析了目前提出的三种RPC单轴受压应力—应变关系的优缺点，为同类问题的研究奠定了基础。

活性粉末混凝土，单轴受压试验，应力—应变关系

0 引言

活性粉末混凝土(Reactive Powder Concrete，简称RPC)为水泥和矿物掺和料等活性粉末材料、细骨料、外加剂、高强度微细钢纤维和/或有机合成纤维、水等原料生产的超高强增韧混凝土[1]。文献[2]对相关文献中RPC的材料性能试验进行总结表明，RPC的立方体抗压强度可达200 MPa～800 MPa，抗拉强度可达20 MPa～150 MPa，断裂能可达30 kJ/m2(普通混凝土的断裂能只有约103 J/m2)，并且具有极低的渗透性、抗硫酸盐侵蚀、抗化学溶液侵蚀及耐磨性等特点，其氯离子扩散系数为普通混凝土和高性能混凝土的2%～3%。RPC具有高强、耐久性较好的特点，因而在工程结构中具有很好的应用前景，且目前已大量应用于桥梁结构。在对RPC结构构件进行分析时，其单轴受压应力—应变关系是重要的基础。目前的相关研究文献十分有限[3-8]，本文对RPC单轴受压应力—应变关系的研究进行了综述分析，为后续的研究和工程结构分析提供参考。

1 基于受压全曲线几何特征的多项式和有理分式分段表达拟合本构曲线

文献[3]对一组三个200 MPa级的配钢纤维的RPC试块进行单轴受压试验，通过对试验数据进行分析，得到RPC单轴受压应力—应变关系：

(1)

(2)

其中，ε和ε0分别为RPC的压应变和峰值应变；fc和fc0分别为RPC的压应力与抗压强度。通过试验数据拟合，建议a和α分别取1.2和8。

文献[4]对三组配钢纤维的RPC试块进行单轴受压试验，通过分析得到RPC单轴受压应力—应变关系：

(3)

通过试验数据拟合，建议a和α分别取1.1和3。

文献[5]对100 MPa级加玄武岩纤维和不加玄武岩纤维的RPC单轴受压应力—应变关系进行研究，同样采用式(3)进行拟合，建议加玄武岩纤维的参数a和α分别取1.1和3，不加玄武岩纤维的RPC的参数a和α分别取0.9和4。

文献[6]基于过镇海提出的多项式和有理分式分段表达的式(9)进行修正，对试验数据进行拟合，得到配钢纤维的RPC单轴受压应力—应变关系：

(4)

A=12.5λ-25λ2-0.57

(5)

B=213.75λ-487.5λ2-22.86

(6)

α=87.45-756.25λ+1 687.5λ2

(7)

其中,λ为水胶比，0.2≤λ≤0.24。

2 基于损伤力学推导的单轴受压本构曲线

文献[7]假定RPC在单轴受压状态下损伤变量服从韦伯统计分布，并通过损伤演化方程的推导，得到RPC单轴受压应力—应变关系如下：

(8)

其中，E为配钢纤维RPC的弹性模量。参数m通过单个试件的抗压试验拟合后，取值为4.452 1。

3 Collins修正本构曲线

文献[8]对大量的钢纤维活性粉末混凝土单轴受压试验数据进行分析，采用Collins等[10]提出的混凝土单轴受压应力—应变关系进行修正，得到如下RPC单轴受压应力—应变关系：

(9)

其中，

(10)

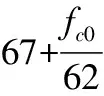
(11)

钢纤维活性粉末混凝土单轴受压强度fc0、峰值应变ε0以及弹性模量Ec均按下式计算：

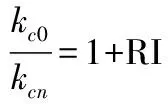
(12)

(13)

其中，kc0为钢纤维活性粉末混凝土的强度、峰值应变或弹性模量；kcn为相应于kc0不加钢纤维的活性粉末混凝土的强度(fck)、峰值应变或弹性模量。参数a1和b1通过回归分析得到，计算强度时取值分别为0.29和0.001 3，计算峰值应变时取值分别为0.52和0.002 6，计算弹性模量时取值分别为0.2和0.000 92。RI为钢纤维加强指标；Vf为钢纤维的体积分数；Lf为钢纤维长度；Df为钢纤维直径；df为钢纤维端部形状修正系数(平直、弯钩和波纹形状分别取1，2.0和1.5)。

不加钢纤维的活性粉末混凝土的峰值应变εc0和弹性模量Ec按下式计算：

(14)

(15)

(16)

fcu=fck+Δf

(17)

(18)

其中，式(14)，式(15)分别为文献[10]和文献[11]的公式。通过不同的公式与试验结果的比较分析，式(14)与式(15)的计算误差最小。

4 结语

目前对活性粉末混凝土单轴受压应力—应变关系的研究还十分有限，上述基于受压全曲线几何特征的多项式和有理分式分段表达拟合本构曲线和基于损伤力学推导的单轴受压本构曲线没有考虑钢纤维含量或玄武岩纤维含量的影响，且仅仅根据非常少的单轴受压试验进行简单的回归，缺乏合理性和适用性。已有的研究表明[12]，活性粉末混凝土的轴心抗压强度、弹性模量与峰值应变随着钢纤维含量的增加而线性增大，在本构曲线中考虑钢纤维含量的影响是十分必要的。而Collins修正本构曲线考虑了钢纤维含量的影响，并且基于大量的试验数据进行分析，具有更广泛的适用性，但其对应力—应变曲线下降段的描述还不够理想，这是该曲线的一个缺点。鉴于目前对活性粉末混凝土的单轴受压应力—应变曲线研究的严重不足，大量开展进一步的研究工作势在必行。

[1] GB/T 31387—2015，活性粉末混凝土[S].

[2] 刘娟红,宋少民.活性粉末混凝土:配制、性能与微结构[M].北京:化学工业出版社,2013.

[3] 马亚峰.活性粉末混凝土(RPC200)单轴受压本构关系研究[D].北京:北京交通大学,2006.

[4] 吴有明.活性粉末混凝土(RPC)受压应力-应变全曲线研究[D].广州:广州大学,2012.

[5] 沈 涛.活性粉末混凝土单轴受压本构关系及结构设计参数研究[D].哈尔滨:哈尔滨工业大学,2014.

[6] 黄政宇,谭 彬.活性粉末钢纤维混凝土受压应力-应变全曲线的研究[J].三峡大学学报(自然科学版),2007,29(5):415-420.

[7] 程臻赟.活性粉末混凝土单轴受压本构模型研究[J].中国水运,2012,12(12):87-88.

[8] Bae B I,Choi H K,Lee B S,et al.Compressive Behavior and Mechanical Characteristics and Their Application to Stress-Strain Relationship of Steel Fiber-Reinforced Reactive Powder Concrete[J].Advances in Materials Science and Engineering,2016(6)：218.

[9] 过镇海.混凝土的强度和变形:试验基础和本构关系[M].北京:清华大学出版社,1997.

[10] Collins M P,Mitchell D， MacGregor J G..Structural design considerations for high-strength concrete[J].Concrete International,1993,15(5):27-34.

[11] Korea Concrete Institute.Concrete Design Code and Commentary[M].Kimoondang Publishing Company,Seoul,Korea,2012.

[12] 闫光杰.活性粉末混凝土单轴受压强度与变形试验研究[J].华北科技学院学报,2007,4(2):36-40.

Review on the stress-strain relation of reactive powder concrete under uniaxial compression★

Zeng Xiang1,2Zou Juan3Cao Baozhu1

(1.CollegeofCivilEngineeringandArchitecture,HainanUniversity,Haikou570228,China； 2.HainanInstituteofDevelopmentonInternationalTouristDestination,Haikou570228,China； 3.HainanTechnologyandBusinessCollege,Haikou570203,China)

The paper introduces the advantages of the RPC(Reactive Powder Concrete), analyes the advantages and disadvantages of the three RPC uniaxial compressed-strain relation by combining with the research on the relation, so as to lay the foundation for the research on the similar problems.

RPC, uniaxial compressed experiment, stress-strain relation

1009-6825(2017)03-0105-02

2016-11-19 ★：海南省自然科学基金项目(20165208)；海南大学科研启动基金资助项目(kyqd1534)

曾 翔(1983- ),男，博士，讲师； 邹 娟(1984- )，女，硕士，工程师； 曹宝珠(1970- )，男，博士，教授

TU528

A