基于OpenSEES的剪力墙低周反复试验数值分析

程 金 永

(汕头大学，广东 汕头 515063)

基于OpenSEES的剪力墙低周反复试验数值分析

程 金 永

(汕头大学，广东 汕头 515063)

采用有限元软件OpenSEES，对剪力墙进行了数值模拟分析，探讨了剪切作用对顶部侧向位移的影响，并将数值模拟结果与试验结果作了对比，结果显示，该模型比较准确的模拟钢筋混凝土剪力墙的非线性反应。

本构关系，低周反复荷载，滞回曲线，宏观纤维模型

0 引言

钢筋混凝土剪力墙在建筑中充当的角色是不仅在提供足够的侧移刚度与强度去限制地震作用下的非线性行为，还在考虑最大的地震作用的设计中提供可靠的非线性变形能力。一些试验结果表明，在高宽比适当的剪力墙中，弯曲屈服和剪切屈服几乎同时发生。文献[1]建议非线性弯曲与剪切变形被称为剪切弯曲的相互作用(SFI)。在一系列高宽比大于2的剪力墙试验[2，3]中已经发现这种影响，并且表明剪切变形为顶部的侧向位移提供了20%的贡献。目前对剪力墙的剪切效应的低周反复模拟的分析主要是重庆大学杨红课题组[4]在做，他们主要是在纤维模型中考虑非线性剪切效应的方法是直接在截面层次定义非线性剪切恢复力关系，其截面的弯曲刚度，轴向刚度通过纤维模型的方法积分得到，截面的剪切刚度根据定义的截面的剪切恢复力关系得出，将剪切刚度与弯曲、轴向刚度组合后可得到组合截面的整体刚度。然而本文采用新单元SFI_MVLEM单元[5]来探讨剪力墙的剪切效应与弯曲的相互作用。OpenSEES(Open System for Earthquake Engineering Simulation)[6]提供了这一新的单元，本文通过同济大学博士章红梅[7]的试验进行展开研究。

1 OpenSEES中二维SFI_MVLEM剪力墙单元的计算原理

1.1 SFI_MVLEM单元与二维材料FSAM原理

OpenSEES中二维剪力墙SFI_MVLEM单元的模型是基于二维剪力墙的多垂直杆单元(MVLEM[8])基础上考虑剪力与弯矩的相互作用开发出来的。在原始的MVLEM中(见图1)，没有纤维之间考虑剪切和弯曲变形耦合作用，并且把整个模型单元的弯曲变形的单轴单元代替MVLEM单元的宏观纤维。在MVLEM单元上高度为ch位置用水平弹簧单元描述单元的剪切变形。在SFI_MVLEM模型单元方程中，在原始的MVLEM单元中的单轴(宏观纤维)单元被钢筋混凝土中平面膜应变单元代替(如图2所示)。在低周反复荷载的作用下的钢筋混凝土墙单元用基于Fixed-Struct-Angle-Model(FSAM)材料模型的二维连续的钢筋混凝土墙单元模型。每个宏观纤维的墙单元包含混凝土和在水平方向和垂直方向加强钢筋，表现是二维的连续的水平方向与竖直方向的平均轴向应变ε_x和ε_y和平均剪切应变γ_xy以及水平方向的与竖直方向的平均轴向应力σ_x和σ_y和平均剪切应力τ_xy(如图2所示)中nDMaterial FSAM所示。

FSAM是Ulugtekin[9]开发并且由Orakcal[10]扩展的平面应力宏观纤维本构模型，用来描述RC平板单元在平面内的循环加载情况下的条件下的变形特性。在FSAM本构模型中，组成RC混凝土平板单元的钢筋与混凝土的应变场假设是相等的，意味着钢筋与混凝土之间的变形协调一致。然而，钢筋变形行为是在纵向方向的单轴应力—应变，混凝土变形行为采用双轴的应力—应变关系，其方向是根据混凝土的开裂状态时的方向。在RC平板单元平面应变转变为平面应力的FSAM，见图3。

1.2 单轴材料的本构关系及其参数确定

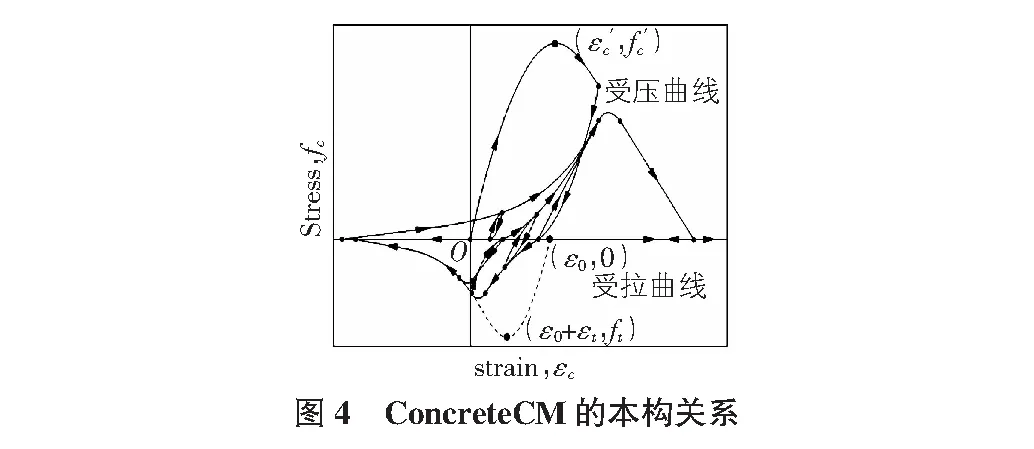
ConcreteCM是1994年由Chang和Mander[11]开发的混凝土单轴滞回模型。这个本构模型是一个提炼的、基于准则、无量纲的本构模型。它描述在受压与受拉情况下的一般混凝土、高强度混凝土的约束与非约束情况下的滞回特性，如图4所示。根据Mander[11]确定不受约束混凝土的峰值受压应变εc、初始弹性模量Ec以及参数rc[12]。可根据Mander[13]的文献和Belarbi[14]的文献来确定约束混凝土的峰值受压应力、峰值受压应变、峰值弹性模量和受拉峰值应力ft与受拉弹性模量Et，在本文中受拉应变取εt=0.000 08。

单轴钢筋材料SteelMPF材料表现出著名的单轴连续非线性滞回特性的材料模型的钢筋材料，是由Menegotto和Pinto[15]开发并由Filippou[16]扩展得到。此模型包括各向同性应变硬化的影响，其曲线关系如图5所示。

2 数值模拟结果与试验结果的比对

为了验证采用本构模型和单元类型的合理性，本文选取同济大学章红梅[7]的博士论文中sw1-1的剪力墙进行模拟，剪力墙高宽比为2.0，高2 000 mm，宽1 000 mm，厚125 mm，边缘约束厚度200 mm，轴压比均为0.1。纵向配筋是6φ10，边缘箍筋是φ6@80，采用混凝土强度为C30，如图6所示。本文通过计算得到弯矩及剪力对侧向位移的影响。

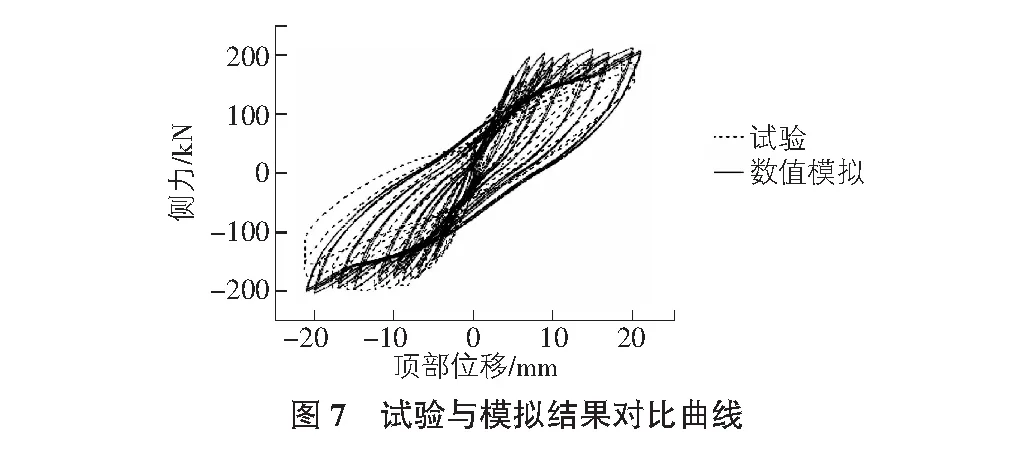
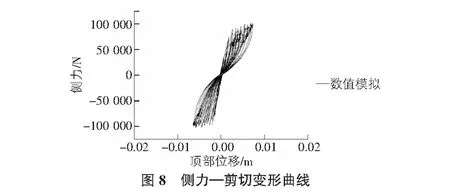
如图7所示，试验与计算结果的滞回曲线的比对，可以看出数值模拟的结果与试验的结果较吻合，加载路径与卸载路径吻合也比较好，SFI_MVLEM单元较好的反映了剪力墙的滞回曲线的特点、加载与卸载刚度的退化、捏拢效应，模拟与试验误差均在10%以内表明单元的合理性。如图8，图9所示，本文计算出了非线性弯曲与剪切变形和在整个低周反复荷载作用过程中的非线性弯曲与剪切变形的耦合作用。在大约110 kN的作用下，弯曲屈服与剪切屈服几乎同时发生。此外，侧力与弯曲、剪切变形作用曲线说明了侧力与弯曲作用体现出很小的捏拢现象，侧力与剪切作用显示出很大的捏拢现象。

3 结语

通过剪力墙sw1-1试验与数值模拟结果的对比分析，本文得出以下结论：

1)采用剪切与弯曲相互作用的多垂直杆单元SFI_MVLEM单元能够较好的模拟剪力墙在低周反复荷载作用下的滞回反应以及耗能特性，验证了非线性有限元软件OpenSEES在模拟剪力墙时的可靠性。

2)SFI_MVLEM计算结果明显的显示了剪切变形与弯曲变形的耦合关系，说明了SFI_MVLEM的单元有效的模拟剪力墙的非线性剪切效应。

[1] Massone, L. M., Wallace, J. W..Load-Deformation responses of slender reinforced concrete walls.ACI Struct. J.,2004,101(1):103-113.

[2] Hines, E. M., Dazios, A., Seible. F.. Seismic performance of hollow rectangular reiforced concrete piers with highly-confined boundary elements phase Ⅲ:Web crushing tests. Rep.No.SSRP-2001/27,Univ. of California, San Diego,2002:239.

[3] Thomsen, J. H.,Wallace, J. W..Displacement-based design procedures for slender reinforced concrete structural walls-Experimental verification. J. Struct. Eng.,10.1061/(ASCE) 0733-9445(2004)130:4(618)-630.

[4] 杨 红，张 睿，藏登科，等.纤维模型中非线性剪切效应的模拟方法及校核[J].四川大学学报，2011,43(1):126-127.

[5] Kolozvari K., Orakcal K., Wallace J.W..Modeling of cyclic shear-flexure interaction in reinforced concrete structural walls. Ⅰ: Theory.ASCE, J. Struct. Eng.,2015，141(5):54.

[6] Mazzoni S, McKenna F,Scott M H, et al. OpenSEES users manual[J].PEER, University of California, Berkeley,2004(18):56-57.

[7] 章红梅.剪力墙结构基于形态的抗震设计方法研究[D].上海：同济大学博士学位论文，2007.

[8] Orakcal, K..Nonlinear modeling and analysis of slender reinforced concrete walls. Ph.D. dissertation, Dept. of Civil and Environmental Engineering , Univ. of California, Los Angeles，2004.

[9] Ulugtekin, D..Analytical modeling of reinforced concrete panel elements under reversed cyclic loadings. M.S. thesis, Bogazici Univ., Istanbul, Turkey，2010.

[10] Orakcal, K., Ulugtekin, D., Massone. L. M..Constitutive modeling of reinforced concrete panel behavior under cyclic loading.Proc., 15th World Conf. on Earthquake Engineering, Lisbon, Portugal，2012.

[11] Chang, G.A. Mander, J.B..Seismic Energy Based Fatigue Damage Analysis of Bridge Columns: Part Ⅰ—Evaluation of Seismic Capacity, NCEER Technical Report No. NCEER-94-0006, State University of New York, Buffalo，1994.

[12] Tsai W.T.,Uniaxial Compressional Stress-Strain Relation of Concrete, ASCE Journal of Structural Engineering,1988，114(9)：2133-2136.

[13] Mander J.B., Priestley M.J.N., Park R..Theoretical Stress-Strain Model for Confined Concrete, ASCE Journal of Structural Engineering,1988，114(8)：1804-1826.

[14] Belarbi H.，Hsu T.C.C.,Constitutive Laws of Concrete in Tension and Reinforcing Bars Stiffened by Concrete, ACI Structural Journal,1994，91(4)：465-474.

Parameters research on numerical analysis of low-cyclic loading test of shear wall

Cheng Jinyong

(ShantouUniversity，Shantou515063，China)

Numerical simulation of shear wall under low cyclic are carry out by use of SFI_MVLEM element based micro-fiber model in finite software OpenSEES, explores the influence of shear deformation to top displacement. The comparison of simulated results and experimental results indicates that SFI_MVLEM element can be efficiently used to simulate the hysteresis response and nonlinear response of shear wall.

constitutive relation, low cyclic loading, hysteresis response, micro-fiber model

1009-6825(2017)03-0020-03

2016-11-20

程金永(1990- )，男,在读硕士

TU311.41

A