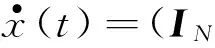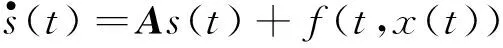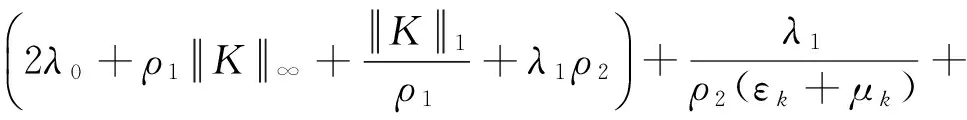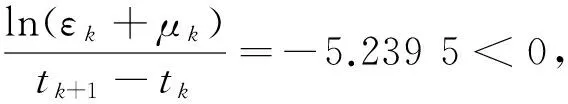一类不连续复杂网络的指数同步研究*
张 兰
(重庆师范大学 数学科学学院,重庆 401331)
一类不连续复杂网络的指数同步研究*
张 兰
(重庆师范大学 数学科学学院,重庆 401331)
研究了具有不连续激活函数的复杂网络受非线性干扰通过时滞脉冲和反馈控制达到指数同步的问题,其中反馈控制和时滞脉冲控制用以克服不连续的激活函数对复杂动力网络造成的影响;基于Filippov解、微分包含、Lyapunov函数方法等,提出了几个充分条件,保证了不连续的复杂动力网络达到指数同步;研究结果是对以前结果的推广和改进,可直接应用于连续复杂动力网络;最后通过数值模拟验证了理论的有效性。
复杂动力网络;指数同步;时滞脉冲控制;不连续激活函数
在过去的几十年中,复杂网络受到了广泛关注,其中复杂网络的同步问题更是研究的重点。但是现在很少有研究者研究不连续激活函数的复杂网络,大部分已经发表的文章研究的都是连续的复杂网络[1-2],不连续激活函数的复杂网络在现实生活中被广泛应用,如激光技术、航天技术、神经网络[3]等,很有研究价值。由于不连续微分方程不具有传统意义下的解,故不能利用传统的方法研究问题,本文在Filippov解的基本理论下对此类问题做出了研究。
现有很多控制技术得到研究[4],比如脉冲控制[1]、间歇控制[2]、自适应同步[5]等。由于脉冲控制只对其中的某些时间点进行控制,大大降低了工作量和成本,所以脉冲控制受到广泛应用。此外考虑到信道的宽度、外界环境的感染等,所以在系统中考虑时滞是不可避免的[6],当然控制在传输过程中也会遇到类似的情况,所以在脉冲控制中考虑时滞也是必须的。但是现有的文章很少考虑时滞对脉冲的干扰,其中文献[7]和文献[8]主要研究带时滞的复杂网络通过脉冲控制达到同步,此文章没有考虑时滞对脉冲控制及信息传输的影响,这种忽略容易导致信息传输发生错误。基于以上原因此处设计了带变时滞的脉冲控制器。
1 基本定义与预备知识
σx(t,xi(t),xi(t-τ(t)))
(1)
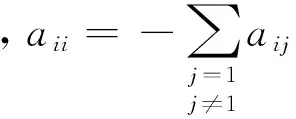
⊗A)x(t)+f(t,x(t))+B⊗Γh(x(t-τ(t)))+σx(t,x(t),x(t-τ(t)))
系统(1)的初值为
xi(s)=φi(s),-τ 系统(1)达到同步即x1(t)=x2(t)=…=xN(t)=s(t), 以下为同步状态系统: ⊗A)s(t)+f(t,s(t)) (2) 它的初始条件可以描述成: s(t)=φ(t),-τ 为了达到同步, 将时滞脉冲控制添加到误差系统中。设e(t)=x(t)-s(t),式(2)与式(1)作差可以得到误差系统如下: (3) 在得出结论之前,需要作以下的假设: 假设H1存在正常数kij,gij,i,j=1,2,…,n,使得f,h满足以下不等式: 对于任意的u,v∈Rn,其中u=(u1,u2,…,un)T,v=(v1,v2,…,vn)T。 因为此处研究的是不连续的复杂动力网络,导致一般意义下微分方程的解是不存在的,所以将引进Filippov解对不连续微分方程进行研究。首先给出Filippov解的定义。 定义1[8]f(x)的集值函数被定义为如下: 定义2[8]对于连续函数ι:[-τ,0]→RN和测度函数ψ:[-τ,0]→Rn,使得ψ(s)∈K[f(ι(s))]对于几乎处处的s∈[-τ,0]都成立,那么系统(1)在初值为(ι,ψ)的问题即为下面的问题:找一对函数[x,γ,α]:[-τ,T]→Rn×Rn×Rn,使得x是系统(1)的解,t∈[-τ,T],其中T>0,γ(t)是f(t)的输出相关函数,α(t-τ(t))是h(t-τ(t)),则系统(1)的初值问题为 与上面相似,系统(2)的IVP问题为 其中的反馈控制u(t)设计如下: u(t)=-re(t)-ηsign(e(t)) 其中r,η>0均为正常数,sign(e(t))=(sign(e1(t)),sign(e2(t)),…,sign(eN(t)))T,sign()为符号函数。 下面假设误差为e(t)=x(t)-s(t),那么误差系统为 其中ν(t)=(ν1(t),ν2(t),…,νN(t))T=γ(t)-β(t),ξ(t)=(ξ1(t),ξ2(t),…,ξN(t))T=α(t)。 定义3[8]如果存在正常数M>1,k>0 对于任何初值都使得: 成立,那么式(3)在控制下达到全局指数同步。 下面给出一些需要的引理: 引理2[1]考虑以下的微分不等式: 假设: 定理1 假设H1,H2被满足,如果存在正常数ρ1,ρ2使得下面不等式(4)—(6)成立: δi+qi+Mi≤ηi (4) εk+μk<1 (5) (6) 证明 定义如下的Lyapunov函数: 其中当t≠tk时,令η=diag(η1,η2,…,ηN),那么有 (7) eT(t)σe(t,e(t),e(t-τ(t))) 对于式(7),一方面,根据假设(H1)和引理1知道存在一个正常数ρ1,使得不等式(8)成立: (8) 对于式(8)的另一方面,类似于上面的方法,存在一个正常数ρ2,可以得到下面不等式成立: eT(t)B⊗Γξ(t-τ(t))≤ 令G=(gij)N×N,p=(p1,p2,…,pN)T,则可以得到: eT(t)B⊗Γξ(t-τ(t))≤ eT(t)B⊗Γξ(t-τ(t))≤ 将式(8)(9)代入到式(6)中去,可得到不等式: 综上所述,可以得到下面不等式: (9) 根据引理1和式(9)可以得到下面不等式: 成立,所以带时滞的脉冲控制和反馈控制使得系统(1)指数同步到系统(2)。 推论1 假设H1,H2被满足,并且系统(1)与系统(2)中的函数是连续函数,如果存在正常数ρ1,ρ2使得下面不等式成立: εk+μk<1 其中G=(gij)N×N,p=(p1,p2,…,pN)T,λ1= 在这一部分,将举例说明结果的有效性。 例1 当n=3,N=5,带有不连续激活函数和有界干扰的复杂动力网络系统被描述为 B⊗Γh(x(t-τ(t)))+σx(t,x(t),x(t-τ(t))) (10) 其中x(t)=(x1(t),x2(t),x3(t))T,τ=1,σx(t)=(0.05x12(t),0.2x2(t-τ),0.3sin(x3(t)))T,f(xi)=h(xi)=(0,(5.82-x3)sign(x1),sign(x2)x1)T。 孤立节点被描述为 (11) 图1 式(11)初值为s(0)=(0.45,0.35,8)T的混沌图Fig.1 Chaotic map of system (11) at initial value s(0)=(0.45,0.35,8)T 其中系统的初值为x(t)=(-2,1,-5,-3,2,-3,-6,5,-7,-6,1,-6,-9,5,-2,-5,13,-15,-24,33,-15,-64,43,-25,-8,13,-55,-34,43,-15)T,t∈[-1,0],时滞脉冲中时滞τ1=0.3,εik=-0.5,μik=0.4,所以条件式(4)成立。 根据误差图(图2—4),很明显可以看出误差最后稳定到0,根据误差的定义可以说明系统(1)和系统(2)达到了完全指数同步。 图2 第一个分量的误差图Fig.2 The error diagram of the first component 图3 第二个分量的误差图Fig.3 The error diagram of the second component 图4 第三个分量的误差图Fig.4 The error diagram of the third component [1] YANG X,YANG Z.Synchronization of TS Fuzzy Complex Dynamical Networks with Time-varying Impulsive Delays and Stochastic Effects[J].Fuzzy Set and Systems,2014(235):25-43 [2] YANG X,CAO J.Stochastic Synchronization of Coupled Neural Networks with Intermittent Control[J].Phys Lett A,2009,36(373):3259-3272 [3] 钟斌,何培祥.基于神经网络观测器的起重机吊重摆角速度软测量[J].西南大学学报:自然科学版,2013(10):105-110 ZHONG B,HE P X.Crane Hoisting Soft Swing Angular Velocity Measurement Based on Neural Network Observer[J].Journal of Southwest University(Natural Science Edition),2013(10):105-110 [4] 任海鹏.Ad Hoc网络拥塞检测和控制分析[J].重庆工商大学学报(自然科学版),2016,33(1):73-76 REN H P.Ad Hoc Network Congestion Detection and Control Analysis[J].Journal of Chongqing Technology and Business University(Natural Science Edition),2016,33(1):73-76 [5] YANG X,CAO J.Synchronization of Discontinuous Neural Networks with Delays via Adaptive Control[J].Discrete Dyn Nat Soc,2013(22):133-138 [6] 唐晓勇,刘贤宁.一类恒化器时滞模型的形态分析[J].西南大学学报:自然科学版,2015(5):89-96 TANG X Y,LIU X N.A Chemostat Model with Time Delay Morphological Analysis[J].Journal of Southwest University(Natural Science Ediion),2015(5):89-96[7] GUAN Z,LIU Z,FENG G,et al.Synchronization of Complex Dynamical Networks with Time-Varying Delays via Impulsive Distributed Control[J].IEEE Trans Circ Syst,2010,18(57):2182-2195 [8] YANG X,YANG Z.Exponential Synchronization of Discontinuous Chaotic Systems via Delayed Impulsive Control and Its Application to Secure Communication[J].Communications in Nonlinear Science and Numerical Simulation,2014(19):1529-1543 责任编辑:李翠薇 Exponential Synchronization of Discontinuous Complex-valued Complex Dynamical Network ZHANG Lan (School of Mathematics, Chongqing Normal University, Chongqing 401331, China) Exponential synchronization of discontinuous complex-valued complex dynamical network with nonlinear perturbation via feedback control and time-delayed impulsive control is studied, among which feedback control and time-delayed impulsive control are used to overcome the influence of complex dynamical network caused by discontinuous activation function. Based on the methods such as Filippov solution, differential inclusion, Lyapunov function and so on, this paper proposes some sufficient conditions to guarantee the exponential synchronization of discontinuous complex dynamical network. The results of this paper are promoted and improved by previous results and can be directly applied to the continuous complex dynamical network. Finally, numerical simulations are given to show the effectiveness of the theoretical results. complex-valued complex dynamical network; exponential synchronization; time-delayed impulsive control; discontinuous activation function 10.16055/j.issn.1672-058X.2017.0001.006 2016-05-09; 2016-06-24. * 基金项目:国家自然科学基金(61263020). 张兰(1993-),女,四川南充人,硕士研究生,从事系统控制论研究. O231 A 1672-058X(2017)01-0027-07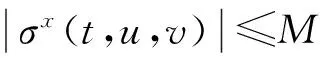


2 主要结果
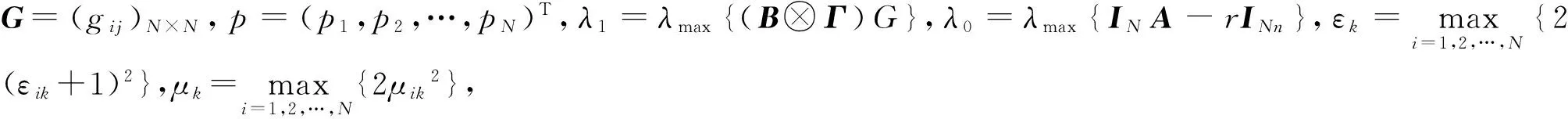
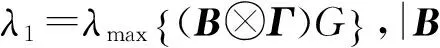

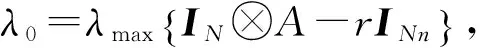
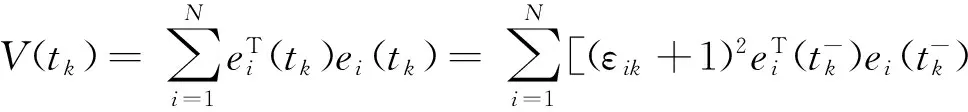
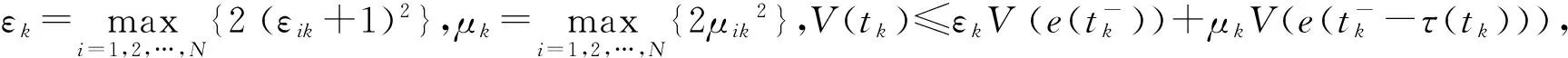

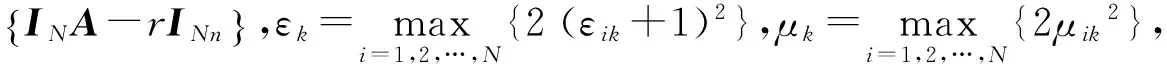
3 应 用