基于优势灰度的变精度粗糙集模型及应用

刘 勇,Jeffrey Forrest，熊晓旋，刘思峰

(1.江南大学商学院，无锡 214122；2.宾州州立SR大学数学系，PA 16057；3.南京航空航天大学经济与管理学院,南京 211106)

基于优势灰度的变精度粗糙集模型及应用

刘 勇1,Jeffrey Forrest2，熊晓旋1，刘思峰3

(1.江南大学商学院，无锡 214122；2.宾州州立SR大学数学系，PA 16057；3.南京航空航天大学经济与管理学院,南京 211106)

由于客观世界的复杂性与不确定性以及人类认知的有限性，现实的决策信息系统总是包括大量的偏好信息、灰色信息、噪声数据，而基于传统粗造集方法难以有效处理。鉴于此，本文利用灰色系统的思想与方法，构建了一种基于优势灰度的变精度粗糙集模型。该方法，利用灰数和灰度的最新研究成果，提出优势灰度的概念，以其确定对象间的优势关系，并将基于优势灰度的优势关系代替变精度粗糙集的不可分辨关系，构建了优势变精度粗糙集模型，最后以实例验证了模型的有效性与适用性。结果表明，通过调整阀值参数，模型具有一定的容错能力，能够有效地提取决策规则，进行科学决策。

偏好信息；灰色信息；优势灰度；变精度粗糙集模型

1 引言

作为一种处理不精确、不确定与不完全数据的理论，粗糙集理论是由波兰科学家Pawlak于1982年提出的[1]，并被广泛地运用到知识发现、数据挖掘、决策分析和模式识别等领域[2-3]。经典粗糙集理论是基于等价关系和等价类提取决策信息系统的决策规则，但是它并没有考虑偏好信息，而现实的决策信息系统总是包含大量的偏好信息，为了有效处理这一问题，Greco等[4-5]将优势关系引入粗糙集模型，构建了优势粗糙集模型。此后，学者基于优势关系对粗糙集方法进行拓展，并将其用于决策分析。Yao和Sai[6]将含有偏好信息决策信息系统转换成二元信息表，构建了基于二元信息表的对象排序方法，并对实际问题进行决策分析；Greco等[7-8]针对不同的应用背景定义了几类优势关系，构建了相应的优势粗糙集决策模型；Sun Bingzhen等[9]研究了序值信息系统，构建了基于优势关系的粗糙集决策方法；骆公志和杨晓江[10]利用变精度粗糙集和信息熵理论，构建了基于条件信息熵的优势变精度粗糙集模型；翟永健和张宏[11]将变精度粗糙集方法与多粒度粗糙集方法进行融合，构建了基于优势关系的多粒度粗糙集模型； Yang，Xibei等[12-13]人改进了以往基于偏序关系的粗糙集模型，提出用更为简便的优势关系来获得属性约简和进行规则提取； Qian Quhua，Liang Jiye等[14-16]针对区间值信息系统提出一种新的优势关系，通过比较区间数的上边界和下边界的大小关系，给出了区间数据优势度、整体优势度的度量，构建了区间数据优势度排序决策方法，同时对集值序值信息系统进行了深入探讨，提出一种新的优势粗糙模型，并将其应用到决策性能评价；施玉杰, 杨宏志和徐久成[17]针对Qian Yuhua等[15]所提出的优势关系的局限性，提出一种α-先验概率优势关系，并定义基于先验概论优势关系的粗糙集模型；Song Peng等[18]针对目前区间值序信息系统决策的局限，提出了有向距离指数排序准则，并结合优势度排序准则，建立了区间数据两级排序决策方法，而李佳， 梁吉业和庞天杰[19]基于信息量的属性重要性度量引入到优势度排序方法；针对现实的决策信息系统包含大量的模糊信息和偏好信息，Hu Qinghua等[20]提出了模糊偏好关系，并将其代替模糊粗糙集的模糊等价关系，构建了模糊偏好粗糙集模型；针对决策信息系统为模糊信息系统和直觉模糊信息系统，黄兵等学者[21-24]分别构建了优势模糊粗糙集群决策模型和优势直觉模糊粗糙模型，设计了属性约简和规则提取方法，而Liu Yong和Li Lin[25]设计了一种新的直觉模糊优势关系，利用其代替等价关系，构建了优势直觉模糊粗糙集，并给出求解约简的算法，同时Liu Yong等[26]针对直觉模糊决策信息系统的特性，提出冲突距离的概念，构建了基于冲突距离的变精度粗造集模型，并利用其解决决策问题。

纵观优势粗糙集模型相关研究，其大多是基于完备偏好信息系统、不完备偏好信息系统、集值偏好信息系统、区间偏好信息系统、模糊偏好信息系统构建优势粗糙集模型，当信息系统含灰色信息、噪声数据时，这些模型难以有效处理，精确实现信息挖掘和规则提取。鉴于此，针对决策信息系统为灰色偏好信息系统，利用灰色系统的思想与方法，提出优势灰度的概念，构建了一种基于优势灰度的变精度粗糙集模型，并研究了模型的性质，最后以实例验证了模型的有效性与适用性。

2 优势灰度

由于客观世界的复杂性、不确定性以及人类认知的有限性，现实的信息系统总是包含大量灰色信息、偏好信息以及噪声数据，而灰色系统是描述和刻画现实的不确定性，解决现实问题的一种新方法，该方法用灰数来描述不确定性信息，既考虑了区间数的变动范围又考虑了可能性分布不同对区间内各取值的影响，可以统筹兼顾模糊数学、概率统计、区间数这三种方法的优点，能够更贴切地描述实际问题[27-29]，鉴于此，利用灰数和灰度的最近研究成果，定义优势灰度的概念。

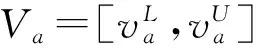
(1)

为对象xi和xk关于属性a的一般优势灰度

其中，ria与rka分别为对象xi和xk关于属性a的取值规则，而μa(Ω)为属性a的背景值测度。

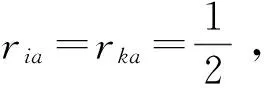
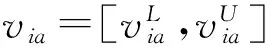
(2)

为对象xi和xk关于属性a的基于核的优势灰度。

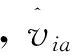
性质1 若μa(Ω)=0，则对象xi和xk关于属性a的优势信息也是明确的，且GDDa(xi,xk)=1/2。

证明：(略)。

注：一般情况下，由于客观世界的复杂性、不确定性以及人类认知的有限性，背景值总是包含一定的灰信息，因此，属性值测度不可能为0。

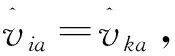
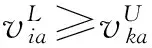
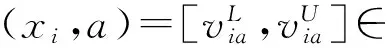
性质2 基于优势灰度的优势关系具有自反性。

证明：由优势灰度的定义，易证(略)。

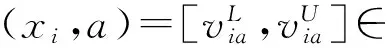
证明：(略)。

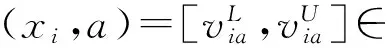
证明：(略)。

性质5 基于优势灰度的优势关系具有传递性。

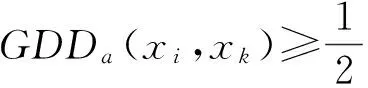
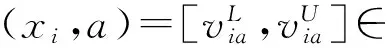
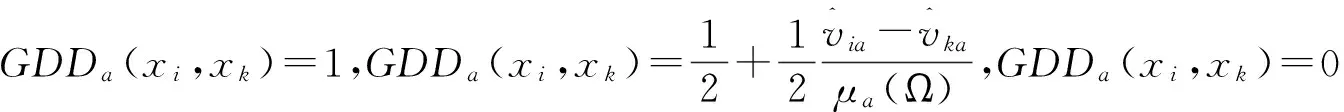
3 灰色变精度粗糙集模型

3.1 模型构建

针对现实的决策信息系统总是包含大量的偏好信息、灰色信息、模糊信息，经典粗糙集模型显得力不从心，本文将优势灰度引入变精度粗糙集模型中，以基于优势灰度的优势关系代替变精度粗糙集的等价关系，构建一种新的变精度粗糙集模型。

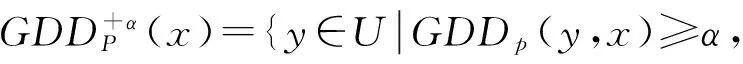
(3)

(4)

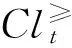
(5)

(6)

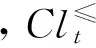
(7)

(8)

(9)

(10)

则有，基于优势灰度的变精度粗糙集的近似精度、近似质量可分别定义为：

(11)

(12)

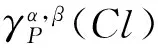
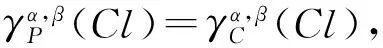
3.2 模型性质

定理 1 在灰色偏好信息系统GS=(U,A,⊗V,f⊗)中，对于∀P⊆C，Clt⊆D，t∈{1,2,…,n}， 给定阀值α∈(0.5,1]，0.5<β1≤β2≤1，则有：

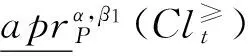
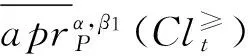
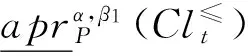
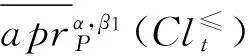
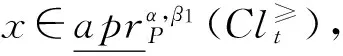
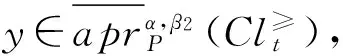
对于③和④，可以采用类似⑴和⑵方法，证明(略)。

定理2 在灰色偏好信息系统GS=(U,A,⊗V,f⊗)中，对于∀P⊆C，Clt⊆D，t∈{1,2,…,n}， 给定阀值β∈(0.5,1]，0.5≤α1≤α2≤1，则有：

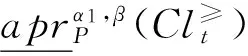
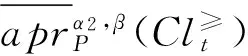
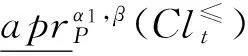
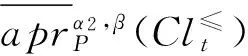
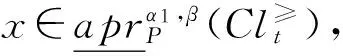
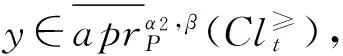
③和④的证明分别类似与①和②，略。

4 案例分析

火炮武器性能直接关系着作战的效果，评估火炮武器性能，选择适合部队需要的火炮，具有重要的意义和作用。在火炮武器性能评估中，如何有效获取影响武器性能评估的关键因素和瓶颈因素、确定火炮武器性能优劣是一项重要的研究任务，本文尝试利用所构建的模型评估火炮武器性能，识别影响火炮性能的重要因素。根据实际需要，部队一般邀请实战人员、火炮设计工程师等专家从火力突击能力指数、反应能力指数、机动能力指数、生存能力指数等方面对火炮武器性能进行评估，在评估过程中对不同属性的偏好程度是不一样的，同时由于客观世界的复杂性、不确定性以及人类认知的有限性，所获得评估值以区间灰数的形式表示往往更为恰当。针对某部队对军工企业提供的8种系统系列火炮进行评估数据，可建立灰色决策信息系统，所表1所示。方案集U={x1,x2,…,x8}，分别代表8种系列火炮；条件属性集C={a1,a2,a3,a4}，其中a1,a2,a3,a4分别为火力突击能力指数、反应能力指数、机动能力指数、生存能力指数；决策属性集为D={d}={0,1}，其中，0表示差，1表示好。

本文所采用指标均为效益型，因此对于其大小比较结果与基于优势灰度的区间灰数的比较结果同方向。根据条件属性集合，通过设定优势灰度阀值对论域进行划分，可得相应的类别，这里我们以α=0.52和α=0.55为例，对论域进行划分：

当优势灰度阀值α=0.52时，基于优势灰度的条件属性集可以将论域划分为U/C={X1,X2,X3,X4}，其中，X1={x1,x3,x8}，X2={x2} ，X3={x4}，X4={x5,x6,x7}。

当优势灰度阀值α=0.55时，基于优势灰度的条件属性集可以将论域划分为U/C={X1,X2,X3}，其中，X1={x1,x3,x8}，X2={x2,x4}，X3={x5,x6,x7}。

根据决策属性集合对论域进行划分，可得两个优势类别，其为U/D={Cl1,Cl2}，其中，Cl1={x1,x3,x7,x8}，Cl2={x2,x4,x5,x6}。

根据设定的不同阀值产生的条件类和决策类，确定分类的上下近似，以α=0.52为例，调整置信参数β，获取分类的上下近似，如下：

(1)当α=0.52，β=1时，有：

=0.675

(2)当α=0.52，β=0.65时，

以α=0.52,β=0.65为例求解模型的属性约简，进而提取其决策规则。根据定义5，利用遗传算法可求得约简，其为{a1,a3}，可知该部队在火炮武器评估时更重视的是火力突击能力、机动能力。由约简{a1,a3}，可生成概率决策规则如表2所示。由表可知，各决策规则的置信度(分类质量)，其分别为100%、66.7%。而对于8个评估对象全部被正确分类，即他们的分类质量为100%。根据计算结果表明，在该灰色偏好信息系统中存在噪声数据，使得经典粗糙集难以有效处理；对于固定精度阈值β，调整参数α，随着参数值α变小，对象越能被正确分类，当小到一定程度所有的对象都能够被分类。这表明，通过调整参数α和阈值β，模型具有一定的容错能力和很强的分类能力。

为验证进一步验证模型能够更有效处理含有灰色信息、噪声数据的决策信息系统，选择骆公志等学者[10,29-31]所构建的粗造集模型进行比较分析。采样类似本文所用的属性约简方法，当α=0.52,β=0.65时，基于江效尧等学者[21,30-33]所得到的约简均为{a1,a2}，通过利用基于江效尧等学者[21, 30-33]所构建的粗糙集方法计算得到其分类质量均为62.5%，而利用潘郁等[32]和刘勇等[33]所构建的变精度粗造集模型计算火炮武器采购灰色决策信息系统分类质量，其分别为75%和87.5%。这些方法和模型并不能将所有对象完全分类，这是主要由于火炮武器采购决策信息系统存在偏好信息、灰色信息和噪声数据造成的；利用不可分辨关系的粗糙集模型对案例进行计算，得到所有对象单独为一类，表明分类过细，难以挖掘有用的信息，提取评估的决策规则，造成这样的结果主要是由于信息系统中存在着偏好信息和灰色信息。

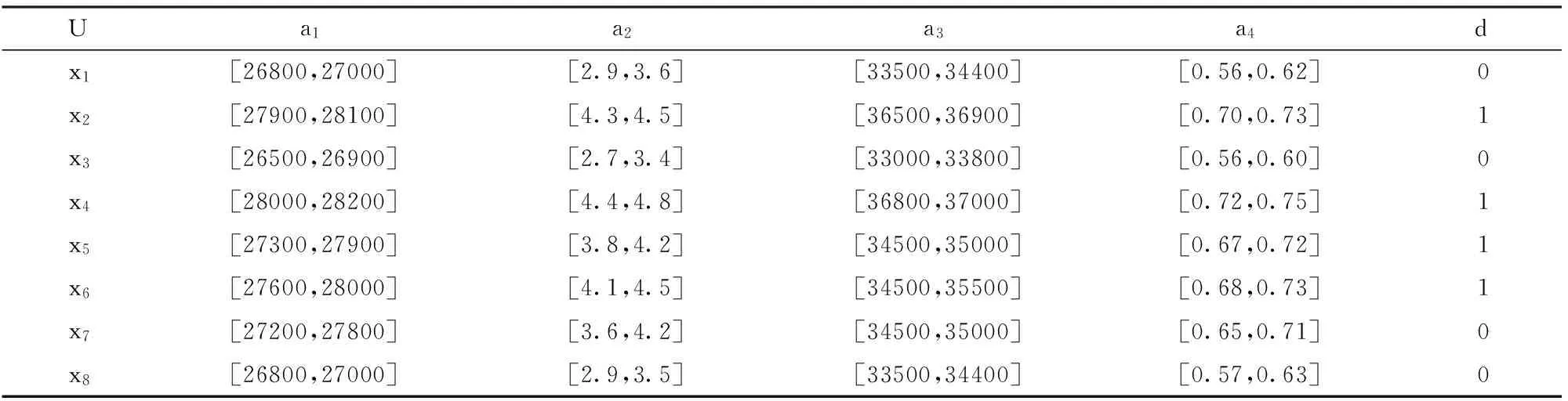
表1 火炮武器采购灰色决策信息系统

表2 由α=0.52,β=0.65时约简{a1,a3}构造的概率决策规则

通过模型分析、案例应用以及方法比较，可知，本文所构建模型能够很好地处理含有偏好信息、噪声数据的灰色信息系统，实现火炮武器评估决策规则的提取。

4 结语

为有效处理含有大量偏好信息、灰色信息、噪声数据的决策信息系统，利用灰色系统的最新研究成果，构建了一种新的优势变精度粗糙集模型，并以实例验证了模型的有效性与合理性。通过模型和案例分析，通过调整参数α和阈值β，模型具有一定的容错能力和很强的分类能力，能够有效提取决策规则，挖掘决策信息系统的所蕴含的规律。

通过模型分析和案例应用，本文所构建的模型主要用于解决决策信息系统为含有大量偏好信息和噪声数据的灰色信息系统，且这类灰色信息系统的属性值一般为数值型。如果决策信息系统的属性值序值型或语义型时，难以利用本模型处理数据，实现对决策信息系统决策规则的提取与规律的挖掘，这是本模型的缺陷，也是后期要着手研究和解决的问题。

[1]PawlakZ.Roughsets[J].InternationalJournalofInformationandComputerSciences, 1982, 49(5): 415-422.

[2]PawlakZ,SkowronA.Roughsets:Someextensions[J].InformationSciences, 2007, 177(1): 28-40.

[3] 刘勇, 王育红, 钱吴永. 基于马尔科夫链的动态冲突分析模型[J]. 中国管理科学, 2015, 23 (SI):325-332.

[4]GrecoS,MatarazzoB,SlowinskiR.Roughapproximationofapreferencerelationbydominancerelations[J].EuropeanJournalofOperationalResearch, 1999,117 (1): 63-83.

[5]GrecoS,MatarazzoB,SlowinskiR,etal.Analgorithmforinductionofdecisionrulesconsistentwithdominanceprinciple[J].LectureNotesinArtificialIntelligence, 2001,2005: 304-313.

[6]YaoYY,SaiYing.Miningorderingrulesusingroughsettheory[J].BulletinofInternationalRoughSetSociety, 2001,5 (1-2): 99-106.

[7]GrecoS,MatarazzoB,SlowinskiR.Roughsetsmethodologyforsortingproblemsinpreferenceofmultipleattributesandcriteria[J].EuropeanJournalofOperationalResearch, 2002, 138(2):247-259.

[8]GrecoS,MatarazzoB,SlowinskiR.Roughapproximationbydominancerelations[J].InternationalJournalofIntelligentsystems, 2002, 17(2):153-171.

[9]SunBingzhen,GongZengtai,ChenDegang.Roughsettheoryforinterval-valuedfuzzyinformationsystems[J].InformationSciences, 2008, 178(8):1968-1985.

[10] 骆公志, 杨晓江.变精度优势粗糙集属性约简择优算法[J]. 中国管理科学, 2009,17(2):169-175.

[11] 翟永健, 张宏. 不完备信息系统中的优势关系多粒度粗糙集[J]. 南京理工大学学报, 2012, 36(1): 66-72.

[12]YangXibei,YangJingyu,WuChen,etal.Dominance-basedroughsetapproachandknowledgereductionsinincompleteorderedinformationsystem[J].InformationSciences, 2008, 178(4): 1219-1234.

[13]YangXibei,YuDongjun,YangJingyu,etal.Dominance-basedroughsetapproachtoincompleteinterval-valuedinformationsystem[J].Data&Knowledgeengineering, 2009, 68(11): 1331-1347.

[14]QianYuhua,LiangJiye,DangChuangyinIntervalorderedinformationsystems[J].ComputerandMathematicswithApplications, 2008, 56(8):1994-2009.

[15]QianYuhua,LiangJiye,SongPeng,etal.Ondominancerelationsindisjunctiveset-valuedorderedinformationsystems[J].InternationalJournalofInformationTechnology&DecisionMaking, 2010, 9 (1): 9-33.

[16]QianYuhua,LiangJiye,Songpeng,elta.Evaluationofthedecisionperformanceofthedecisionrulesetfromanordereddecisiontable[J].Knowledge-BasedSystems, 2012,36(12):39-50.

[17] 施玉杰, 杨宏志, 徐久成.α-先验概率优势关系下的粗糙集模型研究[J]. 南京大学学报(自然科学), 2016,(5): 899-908.

[18]SongPeng,LiangJiye,QianYuhua.Atwo-gradeapproachtorankingintervaldata[J].Knowledge-BasedSystems, 2012, 27:234-244.

[19] 李佳, 梁吉业, 庞天杰. 一种基于优势粗糙集的多属性决策排序方法[J]. 南京大学学报(自然科学), 2016,(5): 844-849

[20]HuQinghua,YuDaren,GuoMaozu.Fuzzypreferencebasedroughsets[J].InformationSciences, 2010, 180 (10): 2003-2022.

[21] 江效尧, 黄兵. 优势模糊区间目标粗糙集模型的群决策规则获取及应用[J]. 南京大学学报(自然科学), 2012,48(4):429-434.

[22] 黄兵, 魏大宽. 基于距离的直觉模糊粗糙集模型及应用[J]. 系统工程理论与实践, 2011,3(17): 1356-1363.

[23]HuangBing,LiHuaxiong,WeiDakuan.Dominance-basedroughsetmodelinintuitionisticfuzzyinformationsystems[J].Knowledge-BasedSystems, 2012, 28: 115-123.

[24]HuangBing,ZhuangYuliang,LiHuaxiong,etal.Adominanceintuitionisticfuzzy-roughsetapproachanditsapplications[J].AppliedMathematicalModeling, 2013, 37(12): 7128-7141.

[25]LiuYong,LiLin.IntuitionisticFuzzyRoughSetModelBasedonConflictDistanceandApplication[J].AppliedSoftComputing, 2015,(31):266-273.

[26]LiuYong,LinYi,ZhaoHuanhuan.Variableprecisionintuitionisticfuzzyroughsetmodelandapplicationbasedonconflictdistance[J].ExpertSystems, 2015:32(2):220-227.

[27]LiuSifeng,LinYong.Greysystemstheoryandapplications[M].BerlinHeidelberg:Springer-Verlag, 2011: 169-190.

[28] 谢乃明, 刘思峰. 考虑概率分布的灰数排序方法[J]. 系统工程理论与实践, 2009, 29(4):169-175.

[29]LiuYong,ForrestJ,XieNaiming.Rankinggreynumbersbasedondominancegreydegrees[J].JournalofSystemsEngineeringandElectronics, 2014,25(4):618-626.

[30] 菅利荣, 达庆利, 陈伟达. 基于粗糙集的不一致信息系统规则获取方法[J]. 中国管理科学, 2003,11(4):91-95.

[31] 鲍新中, 张建斌, 刘澄. 基于粗糙集条件信息熵的权重确定方法[J]. 中国管理科学, 2009, 17(3):131-135.

[32] 潘郁, 菅利荣, 达庆利. 多标准决策表中发现概率规则的变精度粗糙集方法[J]. 中国管理科学, 2005,13(1):95-100.

[33] 刘勇, 菅利荣. 杂合灰色聚类与变精度粗糙模糊集的概率决策方法及应用[J]. 管理工程学报, 2013, 27(3):110-117.

VariablePrecisionRoughSetModelandApplicationBasedonDominanceGreyDegree

LIU Yong1, Jeffrey Forrest2, XIONG Xiao-xuan1, LIU Si-feng3

(1. School of Business, Jiangnan University, Wuxi 214122, China;2. Mathematics Department, Slippery Rock University of USA, Pennsylvania 16057, USA;3. College of economics and management, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China)

Due to the complexity and uncertainty of the physical world, as well as the limitation of human ability to comprehend, it is very difficult for the traditional rough set to effectively deal with the real decision making information system consisted of a lot of preference information, grey information and noise data. In view of this, the thought and method of the grey system is used to construct the variable precision rough set model based on dominance grey degree in the paper. The method, to begin with, based on the new results of the grey number and grey degree, the concept of dominance grey degree is proposed to determine the dominance relationship between objects, so that it is used to substitute for the indiscernibility relationship of variable precision rough set, and then the variable precision rough set model based on dominance grey degree is established, and then its natures are discussed, finally an examples is used to validate the effectiveness and applicability of the model. The result shows that the proposed model has a certain tolerant ability by adjusting the threshold parameter, and then it can realize the scientific decision-making by effectively extracting decision rules.

preference information; grey information; dominance grey degree; variable precision rough set model

1003-207(2017)02-0180-07

10.16381/j.cnki.issn1003-207x.2017.02.020

2014-04-10；

2015-12-29

国家自然科学基金资助项目(71503103); 江苏省自然科学基金资助项目(BK20150157); 江苏省社会科学基金项目 (14GLC008); 中央高校基本科研业务费专项基金 (JUSRP11583， 2015JDZD04)；江苏省研究生培养创新工程(SJLX16_0498;KYZZ16_0305)

刘勇(1985-), 男(汉族), 平舆人, 江南大学商学院副教授, 博士, 研究方向: 冲突分析、 软计算， Email: clly1985528@163.com.

C934

A