基于局部保持投影和隐马尔科夫模型的压力机故障诊断方法
黄亚康,李益兵,江 丽,陆 伟
(1.武汉理工大学 机电工程学院,湖北 武汉 430070;2.上汽通用五菱汽车股份有限公司 技术中心,广西 柳州 545007)
汽车冲压线压力机广泛应用于车门、车前盖等冲压件的冲裁成型工作。随着工业制造水平的发展,为了追求高效、高质、低成本的冲压效益,压力机系统日趋庞大,结构复杂性和系统不稳定也随之提高。压力机运行过程中一旦发生故障,会导致生产效率下降、产品精度降低,甚至影响到作业人员的人身安全。目前压力机设备的可靠性和可维修性的管理还局限于人的主观性判断。压力机发生故障引起停机后,由专家根据维修经验来进行逐项排查,直到找出故障原因[1]。在整个维修过程中,大部分时间并不是耗费在维修故障上,而是在找故障原因。因此如何快速识别压力机的故障模式并找出故障原因,成为了压力机设备维修的一个重要内容。
随着人工智能技术的发展,人工智能在机械设备故障诊断和状态识别方面的应用取得了丰硕的成果,但是针对汽车冲压线压力机的故障诊断的研究却很少。目前对压力机和其他机械设备进行宏观故障分析,多是采用基于知识库和推理机的专家系统,通过构建庞大而严密的逻辑网络,对每一个叶节点按照逻辑规则进行推理或者反演,最终找出根节点的故障模式[2]。这种方法需要构建足够庞大的知识库,知识获取比较困难而且推理规则没有学习能力,诊断效率和准确性较低[3]。对机械设备故障基于算法的智能诊断多是针对一种信号类型,对单一信号的特征进行提取和分析,如江丽等对滚动轴承进行故障分析时,采集其振动信号并利用无监督判别投影提取时域和频域等多种特征,再利用KNN分类器进行故障模式的识别[4]。压力机控制系统的运行参数包含成千上万个零部件的数据,如轴承部件的温度、旋转轴的转速、电气系统的参数等,单一信号往往只能表征零部件的局部特征,无法表征设备的宏观状态。因此对压力机进行智能故障诊断需要研究多种信号、多种特征的变化,对多种通道的信息进行融合分析。
流形学习是从高维数据中挖掘潜在的低维流形结构,并构造高维空间到低维空间的非线性映射,从而实现数据的维数约简或可视化,经典的流形学习算法有局部线性嵌入(locally linear embedding,LLE)、拉普拉斯特征映射(laplacian eigenmaps,LE)和等距特征映射(isomap)。局部保持投影(locality preserving projection,LPP)是He等人提出的一种新的非线性流形学习方法,该方法最优化地保留了原始数据样本的嵌入结构[5]。LPP具有良好的分类能力,在数据和图像处理方面得到了广泛的应用[6-7]。隐马尔科夫模型(hidden markov model,HMM)是一种用来描述含有隐含未知参数的马尔可夫过程的统计模型,通过研究观测值序列来分析研究对象的隐含状态,广泛用于词语分词、标注及语音识别等,同时备受故障诊断领域国内外研究者的青睐,在故障诊断方面取得了很好的应用效果[8-10]。笔者综合LPP算法的维度约简优势和隐马尔科夫模型的识别能力,提出一种基于局部保持投影和隐马尔科夫模型的汽车冲压线压力机故障诊断方法。该方法采用局部保持投影算法对压力机运行过程的多源信息进行特征提取和特征维度约简,挖掘高维流形结构中的敏感特征,实现对压力机非线性数据的处理,然后针对每一类故障建立一个HMM分类器,从而实现对多种压力机故障模式的识别。
1 LPP-HMM模型的构建
1.1 局部保持投影算法
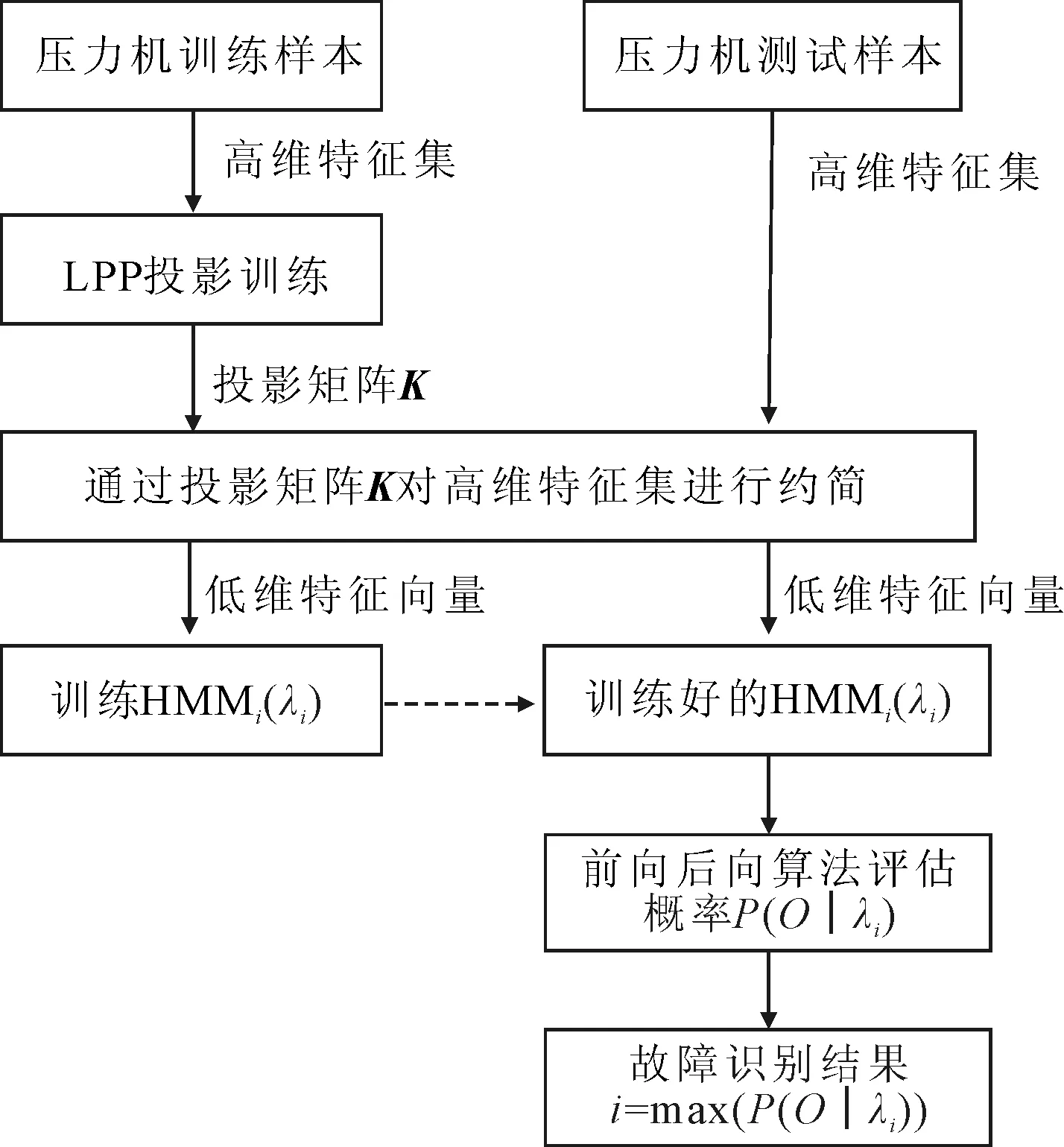
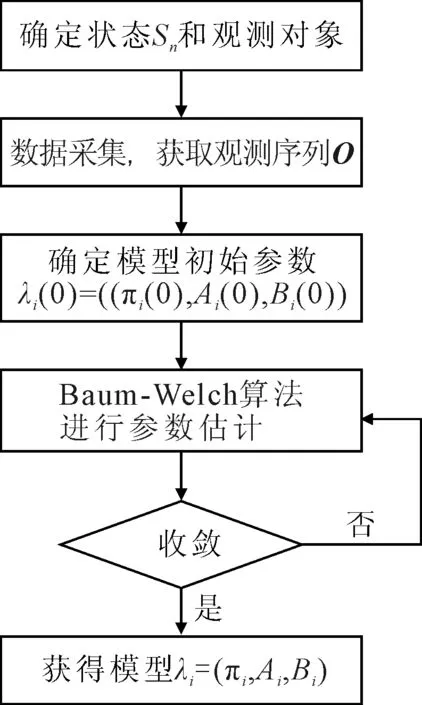
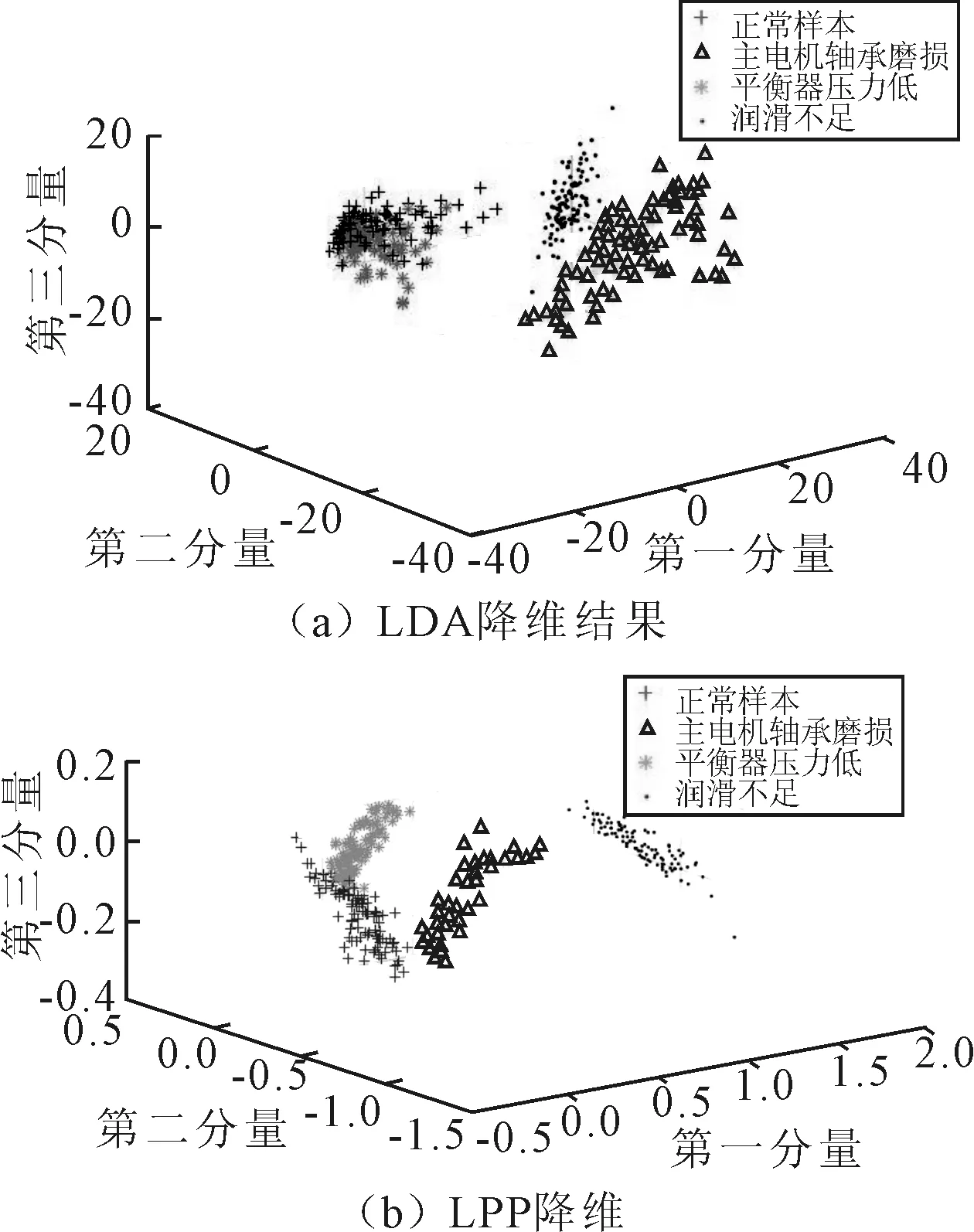
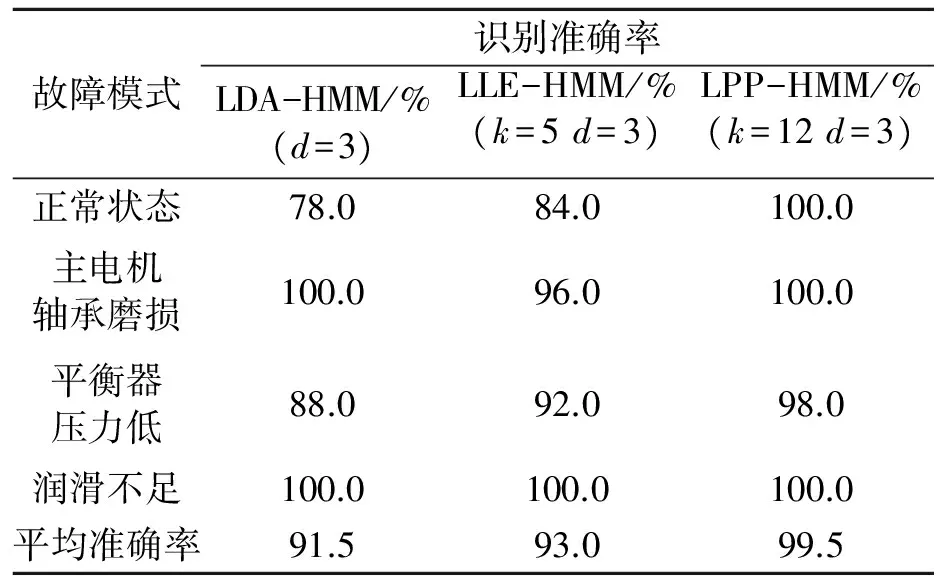
LPP在保持原始高维数据近邻结构的基础上,将其映射到低维子空间,丢弃冗余特征、保留低维敏感特征,能够消除特征提取过程中数据信息损失的影响。给定高维空间Rl上的压力机状态数据样本集X=[x1,x2,…,xN],LPP寻找一个投影方向K使得样本集X映射到低维空间Rd(d< (1) 这里W为一个n×n阶对称矩阵,wij表示xi和xj之间的相似性或近邻性,其数值越大表示xi和xj越接近。当二者没有相关性时wij=0。对式(1)做数学变换可得: 2(KTXDXTK-KTXWXTK)=2KTXLXTK (2) XLXTK=λXDXTK (3) 因此最小的λ对应的特征向量K0即为目标函数Z的最优解。 利用LPP算法对压力机状态数据进行维度约简的过程如下: (1)K邻近法构建邻接图。以与xi欧氏距离最短的k个点为邻近点。若xj在xi的k个最邻近的邻居中,则xj是xi的一个邻近点。 (2)“Heat kernel”法确定权重矩阵W: (4) (3)计算特征值与特征向量,选择d个较小的特征值对应的特征向量ki构成映射矩阵K。 1.2 压力机HMM建模 HMM是Markov链的衍生模型,它的状态不能被直接观测,需要通过对观测矢量的分析来判断,每个观测矢量由一个具有相应概率密度分布的状态序列产生。这是一个双重随机过程:①当前状态转移到下一个状态的概率是随机的;②隐含状态和观测值之间的关系是随机的。一个HMM模型包含如下元素: (1)模型状态数N:S={S1,S2…,Sn}。 (2)观测值数量M:V={v1,v2…,vm}。 (3)状态转移概率:A=[aij]。其中aij表示t时刻状态为Si、t+1时刻状态为Sj的概率。 (4)观测概率B=[bj(m)]。观测概率bj(m)表示在状态Sj下观测到Om的概率。 (5)初始状态概率Π=[πi]。其中πi为在t=1状态为Si的概率。 HMM模型可以用五元组λ=(N,M,Π,A,B)来表示,因此给定模型λ,便可以计算任意时刻模型所处状态的概率。 汽车冲压线压力机在使用过程中,由于磨损、振动,以及零件自身的老化,会出现各种各样的故障模式,如主电机轴承磨损故障、平衡器压力不足故障等。压力机设备的故障诊断实质上就是多种故障状态的识别问题,即从多个模式中找出可能性最大的结果。压力机在运行过程中,其状态通常不能被直接观测到,需要根据设备的故障信号来分析和判断,这与HMM是相通的。因此每种故障模式可以理解为压力机的一种状态,实际运行参数的征兆可以理解为压力机不同状态下的观测值。假设压力机设定了有限的n种故障模式就可以训练n种HMM模型参数,具有3种故障模式的压力机HMM模型的4种状态转移关系如图1所示。 图1 压力机HMM模型4种状态的转移关系 其中S1表示正常状态,S2、S3、S4表示压力机的3种故障状态,通常压力机运行时会发生所有可能发生的故障。当零部件退化或失效时,在没有对其进行维修和维护的情况下,其工作性能只能越来越差,其状态是一个不可逆过程。因此压力机的正常状态可以向任意的故障模式转移,而各个故障模式不能向正常状态转移。模型的状态转移矩阵A可以描述4种状态转移过程中的相关性信息,针对压力机状态的状态转移矩阵A为: (5) 设压力机在t时刻出现各种故障模式的状态的概率为pi(t),则初始状态概率为: πi=pi(t=0)=P{q1=Si} (6) πi描述了观测序列O在t=1时刻系统处于状态Si的概率,压力机初始运行时各项状态指标都是正常的,即π1=P{q1=S1}=1,因此其初始概率为Π=[1,0,0,0]。 由于隐含状态数目N和观测数量M隐含地定义于其他参数中,因此压力机的故障状态HMM模型可以用λ=(Π,A,B)来表示。根据状态转移矩阵A可以计算HMM模型在t时刻系统处于每种状态的概率,即t步状态转移概率为: P(t)=[pi(t)]=(ΠAt-1)A=ΠAt, i=1,2,…,n (7) 通过该模型可以计算系统在任意时刻处于任意状态的概率分布,从而反映出系统状态变化的整个过程。 1.3 基于LPP-HMM的故障识别方法 HMM具有很好的时序建模能力和模式识别能力,因此构建HMM分类器可以有效地识别压力机的故障模式。为了获取全面的故障信息,对压力机的故障状态诊断需要进行多源信息的融合分析,但压力机特征选取的数量和特征的冗余会影响故障诊断模型的精度和复杂度,因此有必要对压力机的运行数据进行特征维度的约简。利用LPP的维度约简特性,可以挖掘压力机故障状态下的敏感特征,结合HMM实现通过多种参数对压力机故障模式的分析。 基于LPP-HMM的压力机故障诊断方法主要包括数据获取、LPP数据降维、HMM模型训练、故障模式识别4个部分,其流程如图2所示。 图2 LPP-HMM故障识别模型 基于LPP-HMM的压力机故障识别的主要步骤如下: (1)原始数据集获取。选取压力机状态参数,选择m种特征,对压力机的n种故障模式分别按相关的规则采集t次,构造高维特征集Xm×t=[xij],i=1,2,…,m,j=1,2,…,t。 (3)N种故障模式的HMM模型训练。初始化隐含状态转移矩阵A、观测状态转移概率矩阵B;以投影后的低维序列Y作为观测值O;通过观测值O采用Baum-Welch算法训练N种故障模式的HMM模型λi=(πi,Ai,Bi),i=1,2,…,N。训练过程如图3所示。 图3 HMM模型训练过程 (4)压力机状态模式识别。采集压力机当前运作下的状态数据获取原始数据集,并对原始样本进行维数约简,获取当前状态观测序列O′,输入n种HMM模型并采用前向后向算法分别计算极大似然概率p(O|λi),最大概率对应的模型即为压力机故障识别结果。 选取某冲压车间冲压线2 250 t的压力机作为实验设备。通过对压力机当前工作状态进行分析,选取了主电机轴承磨损、平衡器压力低和润滑不足3种故障模式。在压力机主传动系统中,主电机长时间工作时会出现轴承磨损、螺栓松动等现象,引起主电机的电流、温度上升和主轴转速的不稳定,而飞轮能量波动、振摆会使飞轮温度上升、滑块运行不平稳。润滑系统是压力机各部件正常运转的关键因素,充分的润滑可以减少压力机各活动部位的表面间摩擦,对润滑点的运动件降温、清洗等作用。当润滑系统油路堵塞、油温超出正常范围时,造成运动副部件润滑不足、摩擦加剧、温度升高。另外,平衡器系统压力低时会使滑块负载增大,主传动系统负载增大引起主电机严重发热,甚至损坏连杆和其他传动部件。基于上述分析,选择了主电机电流、主电机转速、主电机振动、主电机温度、吨位、润滑油压、润滑油温、飞轮速降、飞轮轴承温度、单次冲程时长、平衡器压力、滑块响应时间、过载保护压力、平衡器风压13个特征作为压力机3种故障模式的分析对象。 压力机工作过程将主电机的旋转运动转化成滑块的非匀速往复直线运动,在一个冲程周期内,滑块的任一位置点都能够不同程度地反映压力机的状态。滑块在下行程中的下死点时滑块引导上模具冲击工件,主电机电流、转速、滑块负载等状态参数均发生急剧变化,此刻能很好地反映出压力机的工作性能,因此可对压力机滑块在下死点时的状态参数进行研究,分析压力机的状态。 压力机故障状态识别步骤如下: (1)构造高维特征集。基于OPC通信协议开发压力机监测程序,分别添加采集对象的标签变量,采用订阅方式以50 ms的周期采集数据;根据压力机检修和维修记录,分别筛选同一模具下的润滑系统堵塞引起润滑不足、主电机轴承磨损、平衡器压力降低和正常状态共计4类状态的13种特征数据;筛选出滑块位于下死点(滑块角度为180°)时的数据存为一组构造13维特征向量。 (2)提取低维流形特征。压力机数据的不同特征具有不同的量纲,因此首先对采集到的数据进行归一化处理,消除不同量纲对数据结果的影响。从高维数据样本中取4类故障模式数据各100组,共获取100×4组数据。选择邻域因子k为12、25、50,选择嵌入维数d为2、3,将数据输入LPP算法进行投影。 (3)HMM参数估计。采用Lloyd算法对k=12、d=3时的4种数据进行特征标量化,分别随机选取50组数据输入HMM模型进行训练。初始时刻的状态转移矩阵通过Matlab随机生成,设置最大迭代步数为20,得到4个HMM模型。 λi=(πi,Ai,Bi)i=1,2,3,4 (4)结果识别。从降维后的数据样本中随机取一种模式下的数据20组作为测试观测序列O′=(o1,o2,…,o20),分别输入到4个HMM模型中,计算观测序列O′在不同模型下的极大似然概率P(O′|λi),最大值对应的模型即为识别结果。 为了验证LPP-HMM模型的有效性和优越性,笔者分别采用线性判别分析(latent dirichlet allocation,LDA)和局部线性嵌入与隐马尔科夫模型相结合来对比LPP-HMM在压力机故障诊断中的识别效果。 采用LDA算法和LPP算法将压力机故障数据约简为3维时的可视化效果如图4所示。由图4可以得出,尽管LDA算法能将润滑不足、主电机磨损这2类故障样本有效区分,但是正常状态和平衡器压力机低这2类故障样本却无法区分;而LPP算法可以把4类故障样本有效区分开来,这就说明在压力机状态数据处理方面,非线性降维方法LPP的效果要优于线性降维方法LDA。 图4 LDA与LPP降维效果对比 采用3种混合模型方法识别4类样本时的平均识别率如表1所示,可见LPP-HMM模型在识别正常状态、平衡器压力低的样本识别率明显高于LLE-HMM模型和LDA-HMM模型;3种识别模型在润滑故障样本识别率上都很高,这是因为润滑故障的出现对压力机的整体性能影响很大,状态参数的整体变化较为明显,相对另外3种样本容易区分。 表1 不同混合模型的故障识别结果 综上所述,相比LDA-HMM模型和LLE-HMM模型,LPP-HMM模型具有更好地挖掘潜藏高维故障数据中的关键敏感信息的能力,其提取的低维流形特征具有较高的压力机状态识别率。 笔者以冲压线压力机为研究对象,通过对压力机故障模式与故障征兆的分析,将局部保持投影算法与隐马尔科夫模型相结合,充分发挥二者的优势,提出了基于LPP-HMM的压力机故障诊断方法。该方法通过提取压力机多种状态参数,构造了原始的高维特征集;利用LPP算法对高维特征进行约简,挖掘潜藏在压力机状态数据中的低维流形结构;通过训练HMM分类器有效地识别了压力机的故障模式,准确地反映了压力机的运行状态。实例表明,相比LDA-HMM模型和LLE-HMM模型,LPP-HMM模型具有更高的故障识别精度,验证了该方法应用于压力机故障识别的可行性。 [1] 李蒙,龙伟,龚莹,等.专家系统在汽车厂压力机故障诊断中的应用[J].南昌大学学报(理科版),2014,38(1):36-40. [2] YANG G M, FAN X H, CHEN X L, et al. Intelligent Control of Grate-kiln-cooler Process of Iron Ore Pellets Using a Combination of Expert System Approach and Takagi-Sugeno Fuzzy Model[J]. Journal of Iron and Steel Research,2016,23(5):434-441. [3] 司景萍,马继昌,牛家骅,等.基于模糊神经网络的智能故障诊断专家系统[J].振动与冲击,2017,36(4):164-171. [4] 江丽,郭顺生.基于无监督判别投影的滚动轴承故障诊断[J].中国机械工程,2016,27(16):2202-2206. [5] He X F, Partha N. Locality Preserving Projections[C]∥Proceedings of the 17thAnnual Conference of on Neural Information Processing Systems. Cambridge:MIT Press,2003:153-160. [6] Yu J B. Bearing Performance Degradation Assessment Using Locality Preserving Projections[J]. Expert Systems with Applications,2011,38(6):7440-7450. [7] 张绍辉,李巍华.基于特征空间降噪的局部保持投影算法及其在轴承故障分类中的应用[J].机械工程学报,2014,50(3):92-99. [8] Mitchell Yuwono, Qin Y, Zhou J, et al. Automatic Bearing Fault Diagnosis Using Particle Swarm Clustering and Hidden Markov Model[J]. Engineering Applications of Artificial Intelligence, 2016,47:88-100. [9] 毛乐琦.基于隐马尔科夫模型的无线传感网节点故障诊断算法[J].计算机应用与软件,2014,31(1):132-135. [10] Jiang H M, Chen J, Dong G M. Hidden Markov Model and Nuisance Attribute Projection Based Bearing Performance Degradation Assessment[J]. Mechanical Systems and Signal Processing, 2016,72-73:184-205.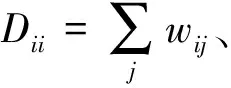


2 压力机故障状态识别
3 结论

