改进初始化方法求解柔性作业车间调度问题

祁文博，郭顺生，赵 国，许 磊

(武汉理工大学 机电工程学院，湖北 武汉 430070)

在经典作业车间调度问题中，待加工工件通常包含多道工序，各道工序间的工艺加工顺序是一定的，且只能在指定的一台加工机器上进行加工。然而在柔性作业车间调度问题中，待加工工件的各道工序可以在指定的多台机器中的一台上进行加工，并且不同机器对应的加工性能不同。相比两种作业车间调度问题，后者减少了对加工工序的机器约束，扩大了调度问题的解空间，使得问题求解过程更加复杂。通常在实际生产过程中，柔性调度问题比经典调度问题应用范围更广，更符合实际生产情况。

通常，求解调度问题的方法分为两类：精确求解法和近似求解法。精确方法主要包括数学规划方法和分支定界法，精确求解法能得到唯一的全局最优解，但其局限于小规模调度问题的求解，并且求解效率不高[1-2]。近似求解法主要包括优先分派规则法、遗传算法、蚁群算法、禁忌搜索算法、模拟退火算法[3-7]等，它能够很快得到问题的解，但不能保证解是最优的，适合大规模问题的求解，不过近似方法得到的解也能较好地满足实际问题的需求。遗传算法源自于生物遗传学的基本规律，它通过模拟生物进化的过程实现对实际问题的求解，具有较强的通用性和对问题解空间的并行搜索能力，得到了广泛的应用。笔者研究的是基于机器选择柔性的作业车间调度问题，采用有效的编码和解码方式，提出了一种新的种群初始化方法，并设计了相应的遗传操作算子，改善了调度问题解的质量和求解速度。

1 问题的描述

柔性作业车间的调度问题描述如下:n个工件在m台机器上进行加工，每个工件Ji(1≤i≤n)至少包含Li(Li≥1)道工序，每道工序的加工机器有多种不同选择，调度问题的目标是为所有待加工件的工序分配加工机器，并确定每台机器上工序的加工顺序，使目标函数达到最优，以满足实际生产的需要。以一个3×5(3个工件在5台机器上加工)的作业车间调度实例进行分析，该实例工序加工时间表如表1所示。

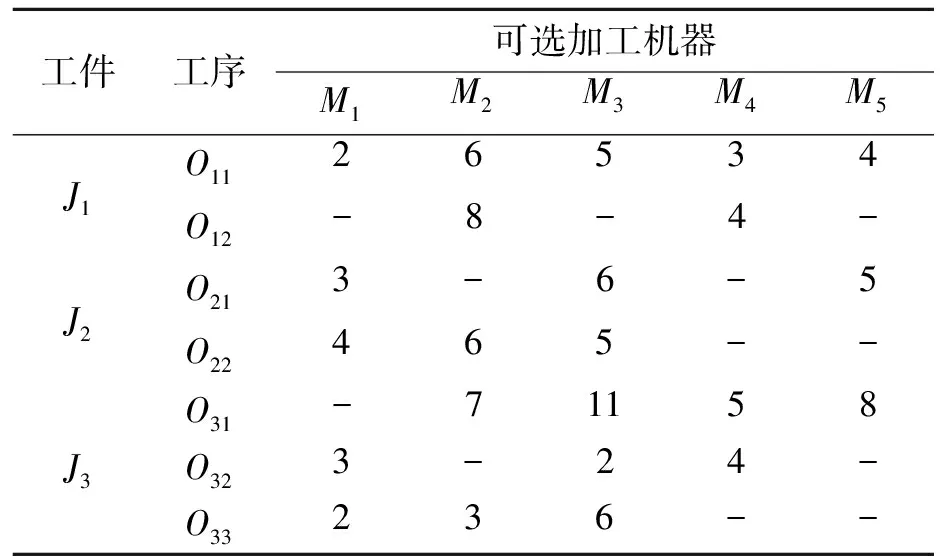
表1 柔性作业车间工序加工时间表

注：“-”表示该工序不能选择对应的机器进行加工。

求解柔性作业车间调度问题解的过程中，需要一定的评价指标来对调度方案的优劣进行评价。笔者考虑两种性能指标：最大完工时间最小、最大机器负荷最小[8]。

(1)最大完工时间CM是指所有工件中，最后一道工序的完工时间。

minCM=min(max(Cji)) 1≤i≤n

(1)

式中：Cji为工件的完工时间；Ji为第i个工件。

(2)最大机器负荷WM是指每台机器上加工时间最长的那台机器。

minWM=min(max(Wk)) 1≤k≤m

(2)

式中：WK为机器k上最后一道工序的完工时间。

以上两种性能指标应满足如下假设条件：

(1)机器约束。同一台机器在某一时刻只允许加工一个工件。

(2)工序约束。同一工件的工序间有先后顺序之分；同一工序只允许被一台机器加工且加工过程必须连续。

(3)其他约束。在加工过程中，机器的调整与设置时间和作业运输时间独立于工序顺序且忽略不计，不考虑作业的取消、机器的崩溃和其他随机性因素。

2 改进遗传算法设计

2.1 染色体编码与解码

结合机器柔性作业车间调度问题的特点，采用分层编码方式对机器基因串和工序基因串进行编码，两基因串的长度相等，都等于待加工工件的工序总数之和[9]。首先确定机器选择基因串，将柔性调度问题转化为经典调度问题进行求解。机器选择基因串用来确定每道工序的加工机器，而工序选择基因串用来确定每台机器上工序的加工顺序，从而确定出调度问题的解。

(1)对于机器选择基因串，每一个基因位表示对应工序可选机器集中的索引位置，如表1中工序O12可选机器集为{M2,M4}，若基因位为1，表示O12选择机器M2，以此类推，如图1所示。

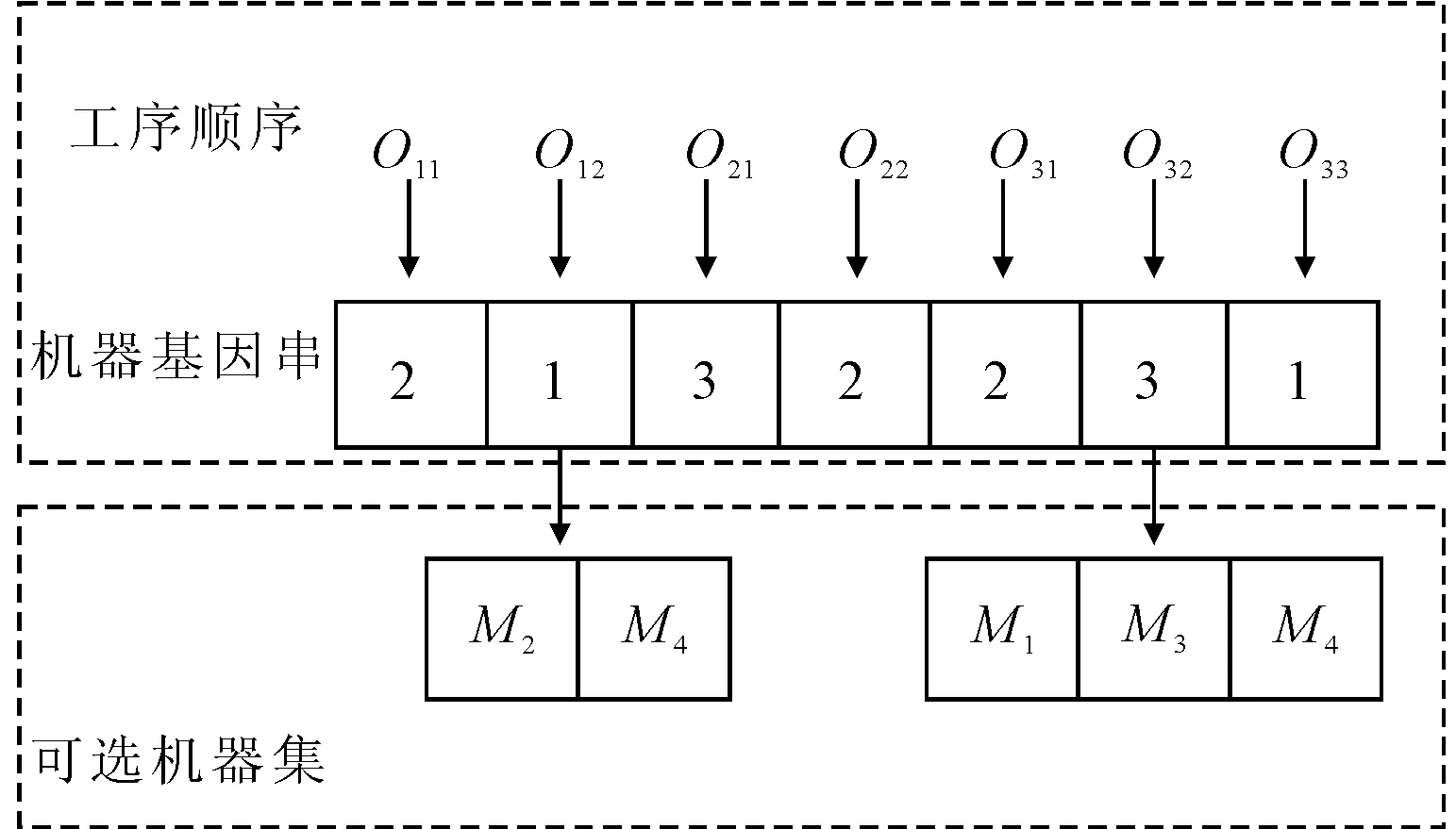
图1 工序基因串

(2)对于工序基因串，每个基因位表示工件号，基因串中相同工件号出现的次数表示该工件的工序总数。其中相同工件号在基因串中出现的位置顺序表示该工件的工序间加工顺序，不同工件号在基因串中出现的位置顺序表示不同工件工序的加工顺序。例如表1中工件号3第1次出现的位置表示工件3的第一道工序O31，以此类推，如图2所示。

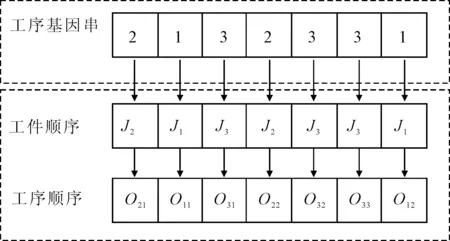
图2 机器基因串

(3)解码过程是将两条基因串所包含的信息转化为一个有序的工序表，然后对表中各工件的工序以最早开始加工时间逐一加工，得到加工系统的调度甘特图。

2.2 适应度函数设计

适应度函数是用来评价种群个体好坏的重要指标，它决定了个体被遗传到下一代种群的可能性大小。通过适应度函数值的大小对个体进行选择，可以保证个体的优良性状被遗传到下一代，从而使得种群的优良基因得以延续[10]。适应度函数具有单值、连续非负等特点，因此采用目标函数的倒数作为评价个体好坏的适应度函数，如式(3)所示。

(3)

式中：f1(x)、f2(x)分别为调度模型的目标函数，因此式(3)可以表示成：

i=1,2,…,n;j=1,2,…,m。

(4)

式中：m为加工系统的机器数；n为工件数；α、β分别为最大完工时间Cmax、最大机器负荷Wmax性能指标的权重比，且α+β=1。

2.3 生成初始种群

初始种群的生成方法是利用遗传算法求解调度问题中的重要环节，它不仅决定了初始种群的质量，还影响着算法的求解效率。目前，利用随机法产生初始种群的情况较多，该方法产生初始种群的质量一般不高，而且也没有考虑加工机器的负荷平衡问题，致使获得最优解或近似最优解的迭代次数增加[11]。笔者提出一种全局搜索和随机生成相结合的方法产生问题初始解，该方法考虑了调度问题的最大完工时间和最大机器负荷两个性能指标，改进了初始种群的质量，平衡了加工机器的工作负荷。全局搜索方法和随机生成法各占初始种群的50%比例。

(1)全局搜索法。新建一个数组，数组长度等于机器选择基因串的长度，该数组用来存放对应工件工序所选加工机器的加工时间。随机选择一个工件，从该工件的第一道工序开始，将可选加工机器的加工时间加到数组的对应位置上，然后将加工时间最短的机器从数组中选择出来并保留，再将数组的其它位置为零，依次类推直到该工件的所有工序选择完毕为止。重复以上步骤，直到最后一个工件最后一道工序选择完毕。而对于工序基因串一般采用随机生成法，将所有加工工序对应的工件号存入一个数组，然后每次随机从数组中取出一个工件号，放入一个新的数组中，循环该操作直到生成工序基因串完毕为止。以表1数据为例，第一次随机选择的工件是J1，第二次随机选择到J2，则执行过程如图3所示。

图3 全局搜索图

(2)随机生成法。以表1中的数据为例进行说明，对工序基因串，首先为每个工件的每道工序随机生成一个(0,1)之间的随机数，然后将随机数按照从小到大的顺序进行重新排序，按照工件号出现的次数得到相应的工序加工顺序，如图4所示。

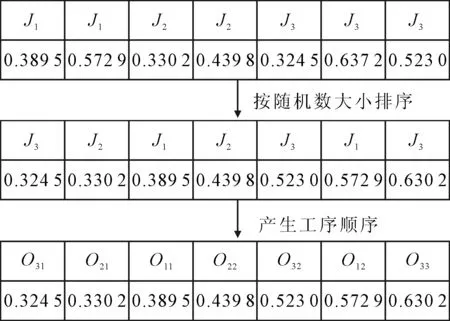
图4 随机法工序基因串

对机器基因串，为每个工件的每道工序随机生成一个[0,1)之间的随机数，如工序O21对应的随机数为0.629 5，它对应的可加工机器为M1、M2、M3，由于0.629 5∈[1/3，2/3]，因此选择机器M2进行加工，如图5所示。

图5 随机法生成机器基因串

2.4 选择操作

选择操作是按照一定的选择概率从种群中将适应度更高的个体选择出来，使种群的优良特性能够遗传到下一代，保证种群的质量[12]。笔者采用锦标赛选择法和精英保留策略两种方法选择个体，锦标赛选择法首先要设定一个概率参数s(一般设为0.8)，然后从种群中随机选择两个个体，同时产生一个0到1之间的一个随机数r，如果这个随机数小于概率参数，则选择适应度值高的个体，否则选择较差个体。被选择出来的个体需要放回到种群，重新参与选择。精英保留策略是将种群中1%的最优个体不经过选择操作直接进入到下一代种群中。

2.5 交叉操作

交叉是将父代个体的部分遗传信息进行交换，以产生新的基因组合的子代。交叉操作使得子代有效继承了父代中的优良信息，也使子代产生了新的遗传信息，是遗传算法的重要操作。对机器选择基因串和工序选择基因串采用相同的交叉概率进行操作，对机器选择基因串采用均匀交叉，对工序选择基因串采用POX交叉[13]。均匀交叉要求基因串的位置顺序不变，随机产生两个交叉位，然后将父代染色体P1、P2的两个交叉位基因遗传到子代C1、C2中，最后将P1、P2染色体中的其余基因位复制到C2、C1染色体中。使用POX交叉方法，首先将全部工件随机划分为两个工件集Js1和Js2，复制父代个体P1和P2中包含在工件集Js1和Js2中的工件到C1/C2，保持子代个体基因位的位置和顺序与父代相同，然后将父代P1、P2中不包含在工件集Js1、Js2中的工件复制到C2/C1，保持它们的顺序不变。

2.6 变异操作

变异操作是对基因串中某些基因位进行改变，以增强种群基因的多样性，改善算法的局部搜索能力[14]。笔者针对机器选择部分和工序排序部分分别设计变异算子。对于可选机器集元素数目大于2的加工工序，随机选择一个不同的机器实现机器选择基因串的变异。对于工序排序基因串，随机选择两个基因位，然后交换两个位置的基因实现工序排序基因串的变异。

2.7 改进遗传算法流程

笔者重点研究了遗传算法的初始化方法，结合该方法设计了改进遗传算法的流程，其具体步骤如下：

(1)确定模型参数，种群规模、概率参数、交叉概率、变异概率和最大迭代次数；

(2)利用笔者提出的复合式初始化方法产生初始种群；

(3)根据适应度函数对种群个体进行评价，利用锦标赛选择法和精英保留策略选择子代种群；

(4)按照交叉概率对种群进行交叉操作；

(5)按照变异概率对种群进行变异操作，生成新一代种群；

(6)判断新一代种群是否满足终止条件，若满足，则输出调度解，若不满足，则返回步骤(3)。

3 算法实例

为了评价算法的性能，选取了研究较普遍的Kacem[15]基准问题，它包括两个8×8和10×10的实例，通过对基准实例的模拟，验证了算法的有效性。改进遗传算法参数设置如下：种群规模P=200，初始种群全局搜索和局部搜索各占50%，概率参数设为0.8，交叉概率设为0.8，变异概率设为0.01，最大迭代次数设为100。

表2给出了柔性作业车间调度8×8实例问题和完全柔性作业车间调度10×10实例问题的两个目标值的计算结果。从表2可看出，相比于传统的遗传算法和Kacem方法，采用改进初始化种群生成方法后，最大完工时间和最大机器负荷均得到了一定程度的改善，而且在实际测试中，同时采用随机生成法和改进的初始化方法进行分别求解后，发现采用改进的初始化方法的求解时间T2短于采用随机初始化方法的求解时间T1，说明在同样满足需求的情况下，改进初始化方法求解效率要高于采用随机生成法的求解效率，更符合实际生产的需要。图6和图7给出了改进后的遗传算法得到的两个实例的最优调度甘特图。

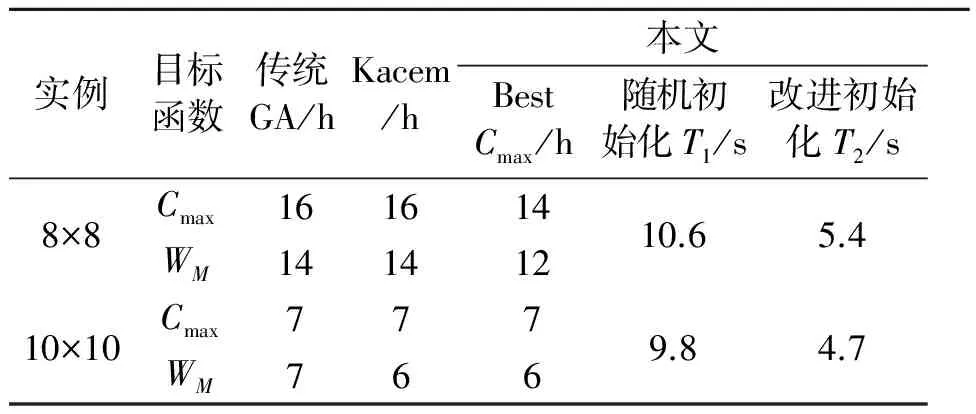
表2 Kacem实例的测试结果比较

图6 8×8基准实例最佳调度甘特图

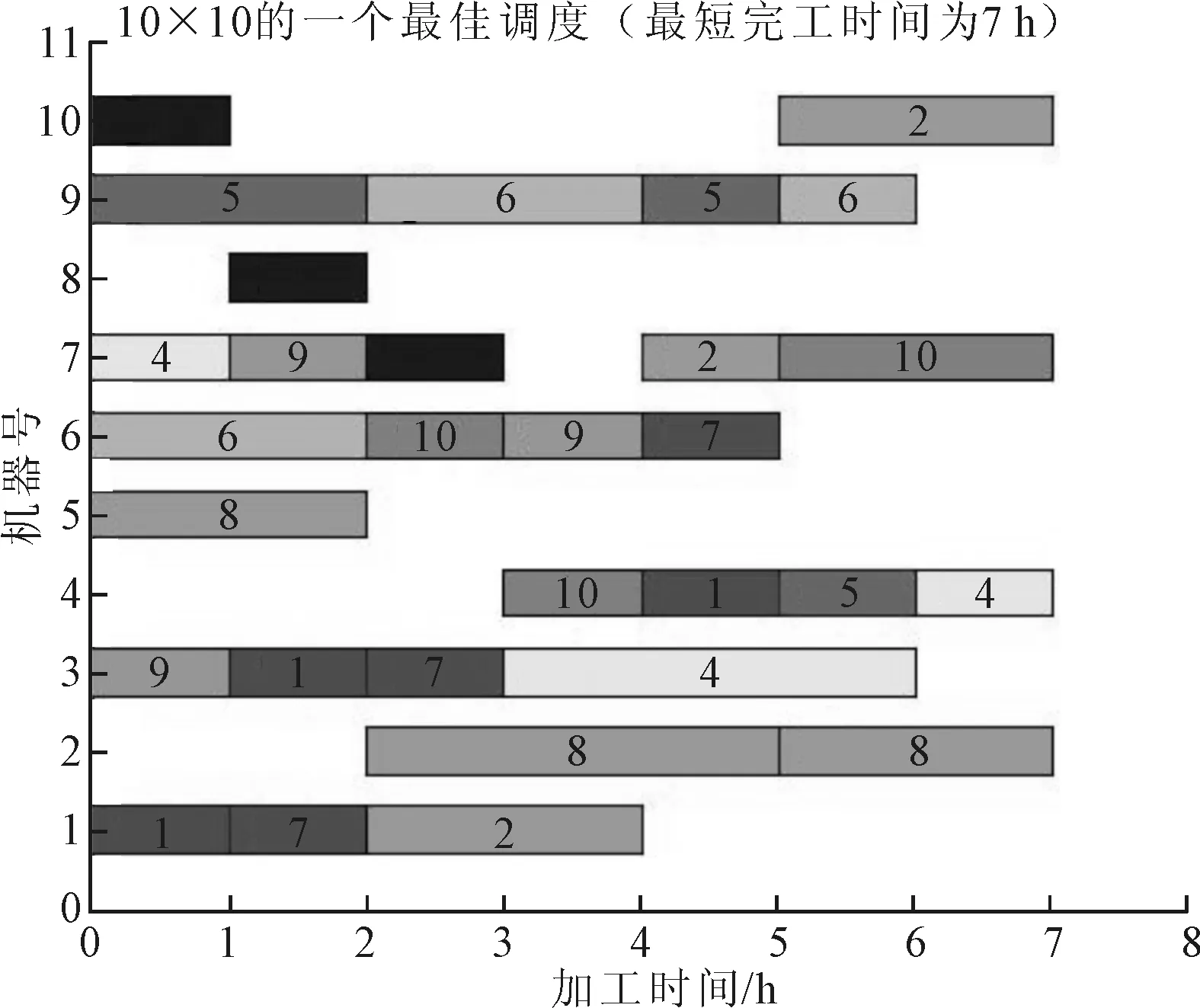
图7 10×10基准实例最佳调度甘特图

4 结论

在基于机器选择柔性的前提下，考虑了最大完工时间、最大机器负荷两个性能指标，基于机器选择和工序排序的分层编码方式进行编码，设计了一种基于全局搜索和随机搜索生成初始种群的复合式方法去求解调度问题的解。笔者采用8×8和10×10标准实例数据进行测试分析，相比于传统的遗传算法，采用复合式的种群初始化方法，不仅提高了初始种群的质量，平衡了各加工机器的工作负荷，而且在求解速度上得到了较大的改善，验证了所提出算法的可行性和有效性。

[1] Chu C,Portmann M C, Porth J M. A Splitting-up Approach to Simplify Job-shop Scheduling Problems[J]. International Journal of Production Research,1992,30(4):859-870.

[2] Mouzon G,Yildirim M B. Single-machine Sustainable Production Planning to Minimize Total Energy Consumption and Total Completion Time Using a Multiple Objective[J].IEEE Transactions on Engineering Management,2012,54(9):585-597.

[3] Ebrahimipour V, Najjarbashi A, Sheikhalishahi M. Multi-objective Modeling for Preventive Maintenance Scheduling in a Multiple Production line[J]. Journal of Intelligent Manufacturing, 2015,26(1):111-122.

[4] Qiu X, Lau H Y K. An AIS-based Hybrid Algorithm for Static Job Shop Scheduling Problem[J]. Journal of Intelligent Manufacturing, 2014,25(3):489-503.

[5] Kundakc1 N, Kulak O. Hybrid Genetic Algorithms for Minimizing Makespan in Dynamic Job Shop Scheduling Problem[J]. Computers & Industrial Engineering, 2016,96:31-51.

[6] Zandieh M, Mozaffari E, Gholami M. A Robust Genetic Algorithm for Scheduling Realistic Hybrid Flexible Flow Line Problems[J]. Journal of Intelligent Manufacturing, 2010,21(6):731-743.

[7] Zorin D A, Kostenko V A. Simulated Annealing Algorithm in Problems of Multiprocessor Scheduling[J]. Automation and Remote Control, 2014,75(10):1790-1801.

[8] Jen J C,Chao C L,Hung C W. A New MCTS-based Algorithm for Multi-objective Flexible Job Shop Scheduling Problem[C]∥IEEE Technologies and Applications of Artificial Intelligence.[S.l.]:[s.n.],2015:413-419.

[9] 杨晓梅，曾建潮.遗传算法求解柔性Job-Shop调度问题[J].控制与决策，2004,19(10):1197-1200.

[10] 张铁男,韩兵,于渤.生产能力约束条件下的柔性作业车间调度优化[J].系统工程理论与实践,2011,31(3):505-509.

[11] 刘琼,张超勇,饶运清等.改进遗传算法解决柔性作业车间调度问题J].工业工程与管理，2009,14(2):59-65.

[12] 张国辉,党世杰.遗传算法求解低碳柔性作业车间生产调度问题[J].组合机床与自动化加工技术,2016(11):141-143.

[13] 张超勇，饶运清，李培根.基于pox交叉的遗传算法求解Job-Shop调度问题[J].中国机械工程，2004,15(23)：2149-2153.

[14] Tang D B,Dai M. Energy-efficient Approach to Minimizing the Energy Consumption in an Extended Job-shop Scheduling Problem[J].Chinese Journal of Mechanical Engineering,2015,28(5):1-8.

[15] Kacem Imed，Hammadi Slim, Borne Pierre. Approach by Localization and Multi-objective Evolutionary Optimization for Flexible Job-shop Scheduling Problems[J].IEEE Transactions on Systems， Man，and Cybernetics，Part C，2002,32(1):1-13.