相位法轮廓测量中光栅近心投射的非线性误差校正算法

陈益松， 翟丽娜， 鲍秋赟

(东华大学 a． 服装与艺术设计学院； b． 现代服装设计与技术教育部重点实验室，上海 200051)

相位法轮廓测量中光栅近心投射的非线性误差校正算法

陈益松a， b， 翟丽娜a， 鲍秋赟a

(东华大学 a． 服装与艺术设计学院； b． 现代服装设计与技术教育部重点实验室，上海 200051)

针对相位法光学测量交叉光轴系统中普遍存在的投影光栅在参考平面非线性变化引起的非线性误差的问题，提出了将非线性问题转换为线性问题的基本逻辑．通过光路的几何关系分别在3种交叉光轴系统条件下推导出光栅相位分布表达式，消除了非线性误差项对解算物点空间坐标的影响，从而使该类问题在理论上得到根本的解决.这对于提高系统测量精度、简化系统标定和后期处理具有重要的意义，使得条纹投影法测量三维物体轮廓更加简便和有效．

三维测量； 轮廓术； 交叉光轴系统； 光栅投影； 非线性相位

在光学非接触三维测量中，有直接三角法[1]和间接三角法两种基本形式．相位测量轮廓术(PMP, phase measuring profilometry)属于间接三角法，其包括傅里叶变换轮廓术[2](FTP， Fourier transform profilometry)和相移法[3-4](PSM, phase shifting method )，两者都可使用正弦光栅进行投射，利用光栅在物体表面相对于参考平面上的相位变化来解算物体表面的三维数据．在相位测量法中，光栅投射有两种基本形式：一种是平行光轴投射方式，该投射方式不存在光栅节距在参考平面变化的问题，但测量区域范围小，需要配合移轴等技术来扩大有效测量区域[5-6]；另一种是交叉光轴投射，该方式利用投影镜头和摄像镜头的视角在测量区域的交叉重叠来取得较大的有效测量区域，但光栅倾斜投射(或摄像机倾斜拍摄)会造成摄像机所拍参考平面上的光栅节距发生非线性变化，给测量带来系统误差．针对这一问题，文献[4]在提出相移法之初便指出需要建立相位与高度的映射关系表，以查表的方式对该误差进行修正．文献[7]提出了一种误差外部补偿算法，此方法需要测量多个角度，计算繁琐并会引入新的误差．文献[8]根据几何关系求得投影光栅条纹周期和参考平面光栅条纹周期间的数学表达式，并对其积分表示出相位，再通过最小二乘法确定出相位幂级数展开式中的未知系数，来估算参考平面上的非线性相位．文献[9]在两个坐标系下求出物体高度和相位之间的关系，并通过定标试验计算出测量系统的误差．文献[10]提出编写一幅特殊的周期不均匀的校正光栅，使得倾斜投影时投射到参考平面上的条纹恰好周期均匀，但实质上其周期校正功能是基于编写的校正光栅实现的．文献[11]也是采用上述方法编写了校正光栅，以此避免参考平面上周期展宽引起的非线性误差．上述方法各异，总体而言属于外部补偿或实测校正，未从理论上直接解决问题，更有许多研究对这种非线性问题予以忽视，直接按远心平行光路以线性方法来解算，这必然会使测量结果不准确[12-13]．因此，寻求消除这种非线性误差的根本解决方法，是该领域学者一直关注的问题．

本文系统阐述了在典型的倾斜投影垂直拍摄或垂直投影倾斜拍摄以及更具一般性的交叉光轴系统条件下，针对光栅非线性变化所引起的测量非线性误差问题，依据非线性相位分布的线性解逻辑，推导出3种系统条件下的参考平面坐标值与摄像机共轭像面非线性相位的映射关系，并根据测量系统参数和摄像机像面的相位变化来求接触物点的坐标，具有普遍适用性．

1 交叉光轴下的条纹周期变化

图1为典型的倾斜投影交叉光轴系统，投影光轴SO和摄像机光轴EO相交于参考平面R于点O，SO相对于参考平面R的倾斜角为α，投影仪到参考平面的垂直距离为l，两光心连线SE与参考平面平行且长度为d，R1为投影仪的共轭像面．

当投影仪倾斜投影时，因为投影仪光轴垂直于共轭像面R1，所以，当采用周期均匀的朗奇(Ronchi)或正弦光栅近心投射时，R1上的光栅图案也是等节距分布的，而参考平面R(x)上的条纹是非均匀分布的，即参考平面上的光栅条纹周期发生改变，频率也发生改变，且越远离投影仪则条纹周期越大.倾斜投影下变周期的朗奇光栅如图2所示．

图2 倾斜投影下变周期光栅Fig．2 The grating with non-uniform period in tilt grating projection

由相位法解算物体轮廓的基本原理可知，物体轮廓点(简称“物点”)相对于参考平面R(x)的高度值,依赖于其存在时摄像机所拍摄到的相位相对于参考平面R(x)上无物体时的光栅条纹的相位变化来解算的[2-4]．因此在相位解调时，若忽略参考平面上光栅条纹本身的周期变化，测量结果必将产生误差．本文通过几何解算出各种交叉光轴下的非线性误差项，并直接给出了光栅在参考平面上相位分布的数学表达式，从理论上根本解决交叉光轴条件下的非线性测量误差问题．

2 非线性相位差的线性解

以相位法轮廓测量的基本坐标系为基础(参见图1)，当正弦光栅条纹投射在被测物体表面时，物体的高度对光栅条纹进行了调制，光栅发生变形，相位发生变化．

设投影光栅在R1平面上的光栅周期为P．若采用远心投影，那么平行光束投射在参考平面R(x)上的光栅空间周期为P0=P/sinα，空间频率为f0=sinα/P，则参考平面上任意点的相位为

φ0(x)=2πf0x

(1)

若采用近心投射发散光束时，参考平面R(x)上光栅周期P1逐渐变大，即频率f1逐渐变小，则R(x)上任意点的相位随着光栅频率的改变而改变，如式(2)所示.

φ1(x)=2πf1x

(2)

直角坐标系中参考平面上平行光束与发散光束的相位偏差示意图如图3所示．

图3 参考平面上平行光束与发散光束的相位偏差Fig．3 Phase deviation between parallel and divergent beam

两曲线的值域之差即为由于投影条纹在参考平面上改变而产生的相位偏差，对于参考平面上的一点C，其相位偏差项为

Δφ(xc)=φ0(xc)-φ1(xc)

(3)

由图3可知，φ1在x=C产生的相位可用φ0在x=B的相位值代替，则

Δφ(xc)=φ0(xc)-φ0(xb)=

(4)

由式(4)可知，非线性相位偏差项Δφ(xc)是由点C与点B的横坐标差值决定的．

3 测量系统的非线性相位分布

3．1 倾斜投影垂直摄像的交叉光轴系统

在图1中，投影仪相对于参考平面的倾斜角为α，入射光线SCA与R1相交于点A．在平行光束下，过R1上点A的入射光线投影在参考平面的B点上，因此，OB相当于OA在R(x)上的线性投影，而BC则为光栅节距的非线性变化部分，该部分在文献[14]中被称为初始相位，即本文所称非线性相位偏差．根据三角几何关系可以推导出该非线性偏差项．

测量系统的参考平面R(x)也是摄像机的共轭像面，像面(X，Y) 坐标与参考平面(x，y)坐标系重合．由几何关系易得△ABC∽△SOC，则

(5)

(6)

R1光栅频率f0平行映射到R(x)上的光栅频率为f01= -f0sinα，则R(x)上的光栅非线性相位偏差为

(7)

根据式(3)，倾斜光栅在参考平面R(x)上实际相位分布为

φ1(x，y)=φ01(x，y)-Δφ01(x，y)=

(8)

在此，摄像机图像相位分布中φ1(X,Y)即为φ1(x,y)，根据式(8)，依据像素点的相位信息就可求解出测量坐标系R(x)的x坐标值．

3．2 垂直投影倾斜摄像的交叉光轴系统

垂直投影倾斜摄像的交叉光轴系统如图4所示，SO和EO分别是投影光轴和摄像机光轴，SO垂直于参考平面R(x)，则投影仪投射在参考平面R(x)的光栅是均匀的．然而摄像机光轴EO相对于参考平面的倾斜角为β，摄像机的共轭像面是R2，不与R(x)重合，即R(x)上的均匀光栅映射到摄像机像面的共轭平面R2上的光栅条纹周期是非线性变化的．

图4 倾斜摄影交叉光轴系统的几何解析图Fig．4 Geometric analysis of the crossed optical axes system with oblique-angle photography

以R(x)上的D点为例，K2为D在摄像机共轭像面R2上的坐标，过点D做垂直于R2的线交于点B2，OB2相当于OD在R2上的线性投影，B2K2则是非线性变化部分．

由几何关系易知△B2DK2∽△OEK2则

(9)

(10)

考虑R(x)的光栅频率f0平行映射到R2上的光栅频率为f02=f0/sinβ，摄像机共轭像面R2上非线性相位偏差为

(11)

根据式(3)，平面R2上光栅像的实际相位分布为

(12)

由式(12)可根据图像的相位φ2解出R2对应的X坐标值，R2上坐标X映射到R(x)的x为

(13)

3．3 一般性交叉光轴系统

图5 一般性交叉光轴系统的几何解析图Fig．5 Geometric analysis of the general crossed optical axes system

在一般性交叉光轴系统中，投影仪光轴和摄像机光轴均倾斜如图5所示，此时的非线性误差则来自投影仪倾斜和摄像机倾斜两个方面．OB1为投影仪在R1平面均匀条纹在摄像机共轭像面R2上的投影，B1B2为投影仪倾斜在平面R2上产生的非线性投影，B2K2为摄像机倾斜在R2上产生的非线性投影，因此，总的非线性投影B1K2=B1B2+B2K2．

(14)

(15)

考虑R1-R(x)-R2的映射关系，R1光栅频率f0平行转折映射到R2光栅频率为f03=-f0sinα/sinβ， 平面R2上光栅像的相位误差为

(16)

根据式(3)，平面R2上光栅像实际相位分布为

(17)

由式(17)可根据图像的相位φ3解出平面R2上对应的X坐标值，可根据式(13)求出R(x)的x相应值．

4 物点坐标的解算

当计算机生成的正弦光栅条纹投射在被测物体表面时，物体的高度对光栅条纹进行了调制，光栅发生变形，在像面坐标系(X，Y)下由摄像机所拍到的光强信息可表示为

I(X，Y)=A(X，Y)+B(X，Y)cos[φ(X，Y)]

(18)

式中：A(X，Y)为背景光强度；B(X，Y)为光栅条纹的振幅；相位函数φ(X，Y)表示被测物体表面形态而引起的相位变化，其由相移法[3-6，15]或傅里叶法[2，16]求得．

在图1、图4和图5中，图像XD点接受参考平面R(x)上D的反射光，而测量物体时，XD点接受W点经D点的反射光，该光线的相位相当于参考平面R(x)上C点即图像坐标XC的入射光相位，D点与C点的距离决定了物体W点在Z轴上的高度．

由φD(XD，Y) 和φC(XC，Y)可根据式(8)、(12)或(17)解算出摄像机共轭像面的XD和XC，再由式(13)转为参考平面R(x)的xD和xC坐标(3．1节中，xD=XD，xC=XC)．

以图4为例，设点W的O-XZ坐标系下的坐标为(xW，zW)，由几何关系△DCW∽△ESW，则

(19)

计算可得

(20)

当W点在参考平面R(x)上方时，zW为正；当W点在参考平面R(x)下方时，zW为负．

虽然W点坐标与xD有唯一的关联性，但xW≠xD，需要根据不同情况进行解算．同以图4为例，△DWF∽△DEG，则

(21)

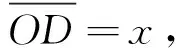
(22)

说明xW不仅与zW有关，还与系统的结构参数及图像坐标X有关．

5 结 语

本文针对一般交叉光轴光学测量系统的光栅非线性变化引起测量误差的问题，给出了将非线性问题转化为线性问题的基本逻辑．通过分析光路图的几何关系，推导出非线性误差表示项，并给出了不同情况下摄像机共轭像面的光栅相位分布表达式．依据不同系统的结构参数，建立参考平面x坐标与共轭像面的光栅相位的映射关系，由物体外轮廓引起的光栅相位变化最终转换参考平面上投影光栅x坐标值的变化问题，并最终根据几何关系解算出物点的空间坐标．本文从最基本的原理出发，推演出的数学模型从根本上解决了一般交叉光轴测量系统因投影光栅非线性变化引起的测量误差问题，也可简化实际测量系统的标定和后期校正问题，使利用光栅条纹投影测量三维物体轮廓的方法更加简便和有效．

[1] 陈益松，夏明．光学三角测量及其在人体测量中的应用[J]．纺织学报，2012，33(12)：95-101．

[2] TAKEDA M， MUTOH K． Fourier transform profilometry for automatic measurement of 3- D object shapes[J]． Applied Optics， 1983，22(24)：3977-3982．

[3] SRINIVASAN V， LIU C H， HALIOUA M． Automated phase measuring profilometry of 3- D diffuse objects[J]． Applied Optics， 1984，23(18)：3105-3108．

[4] SRINIVASAN V， LIU C H， HALIOUA M． Automated phase measuring profilometry: A phase mapping approach[J]． Applied Optics， 1985，24(2)：185-188．

[5] 吴新侠．双频投影光栅应用于人体测量的原理及算法研究[D]．上海: 东华大学服装和艺术设计学院，2010．

[6] 陈益松，吴新侠．双频光栅相位法应用于三维人体测量[J]．东华大学学报(自然科学版)，2011，37(6)：736-744．

[7] SANSONI G， CAROCCI M， RODELLA R． Calibration and performance evaluation of a 3- D imaging sensor based on the projection of structured light[J]． IEEE Trans Instrum Meas， 2000，49(3)：628-636．

[8] CHEN L J， QUAN C H G． Fringe projection profilometry with nonparallel illumination: A least-squares approach[J]． Opt Lett， 2005，30(16)：2101-2103．

[9] 张宗华，彭翔，史伟强，等．实物表面三维相位图定标的研究[J]．仪器仪表学报，2000，21(5)：539-542．

[10] FU Y J， LUO Q． Fringe projection profilometry based on a novel phase shift method[J]． Optics Express， 2011，19(22)：21739-21746．

[11] 严家明，于洪伟，张毛毛，等．基于MATLAB光栅周期校正方法的研究[J]．光学与光电技术，2013，11(3)：27-30．

[12] 刘艳．光栅投影式物体表面三维形貌测量方法的研究与改进[D]．南京: 南京航空航天大学自动化学院，2007．

[13] 姜安．FTP三维物体表面轮廓工程测量方法的研究[D]．天津: 天津科技大学机械工程学院，2003．

[14] 杨国光．近代光学测试技术[M]．杭州: 浙江大学出版社，1997：314-315．

[15] 陈益松，夏明，林琳．光栅相移法用于三维人体测量的实验研究[J]．纺织学报，2013，34(6)：83-87．

[16] 鲍秋赟．傅里叶变换轮廓术在三维人体测量中的应用研究[D]．上海: 东华大学服装与艺术设计学院，2016．

(责任编辑：刘园园)

For the wide existing nonlinear error caused by nonlinear variation of projected grating on reference plane in crossed optical axes geometry of phase measuring profilometry， a basic logic of the nonlinear problem into a linear problem was proposed． The formula of grating phase distribution were deduced through the geometric relationships to eliminate the nonlinear error in three crossed axes systems respectively． This formula can calibrate the phase modulation item in calculating the coordinates of objects， so as to solve this kind of problems fundamentally in theory． It has important meaning for improving accuracy of measurement, simplifing system calibration and post processing. Therefore， it makes fringe projection profilometry flexible and universal in measuring three-dimensional objects．

3D measurement； profilometry； crossed optical axes system； grating projection； nonlinear phase

TB 96

A

Nonlinear Error Correction Method for Entocentric Projection in Phase Measuring Profilometry

CHENYisonga， b，ZHAILinaa，BAOQiuyuna

(a． Fashion & Art Design Institute； b． Key Laboratory of Clothing Design & Technology，
Ministry of Education， Donghua University， Shanghai 200051， China)