微波辐射计海面温度的数据质量控制

王兆徽，刘伟，张琼雄，宋清涛

（1.国家海洋局空间海洋遥感与应用研究重点实验室,北京100081；2.国家卫星海洋应用中心,北京100081；3.庄河市高级中学，辽宁大连146400；4.广东省遂溪县气象局，广东湛江524300）

微波辐射计海面温度的数据质量控制

王兆徽1,2，刘伟1,3，张琼雄4，宋清涛1,2

（1.国家海洋局空间海洋遥感与应用研究重点实验室,北京100081；2.国家卫星海洋应用中心,北京100081；3.庄河市高级中学，辽宁大连146400；4.广东省遂溪县气象局，广东湛江524300）

根据星载微波辐射计反演海洋大气参数的过程，分析了仿真实验中线性反演算法和非线性反演算法对反演结果的数据质量控制能力。AMSR-E观测数据的非线性反演结果分析对仿真实验的结论进行了验证，得到了肯定的结果。实验结果表明：星载微波辐射计的非线性反演算法物理意义明确、结果可靠，有良好的数据质量控制能力，具有业务化应用的潜力。

星载微波辐射计；非线性反演算法；数据质量控制；海面温度

1 引言

目前，使用基于星载微波辐射计微波遥感技术可以方便的获取全球范围内的海面温度、海面风速、水汽含量，液水含量等大气海洋信息，这些信息为全球水循环研究、全球气候变化研究、海洋环境预报与监测、海洋灾害防护、海上执法维权等领域提供了重要的帮助。自1972年美国雨云5号（Nimbus 5）卫星发射至今，星载微波辐射计的观测数据经历了50余年不间断的积累，从星载微波辐射计观测亮温数据到大气海洋参数的反演方法也从线性的统计回归方法发展到非线性的辐射传输模型求解[1]。现今，遥感观测数据的应用处于大数据时代[2]，如何在众多的观测数据以及反演结果中提取有效的信息成为遥感技术的一个重要研究方向[3]。

本文基于非线性反演算法求解过程中的均方误差（Mean Squuare Error，MSE）最小化，对以AMSR-E[4]（Advanced Microwave Scanning Radiometer-Earth Observation System）为例的星载微波辐射计的观测数据进行质量控制，进而筛选出高质量的大气海洋参数，并对观测仪器的硬件设计指标提出改进要求。这种质量控制方法相比于统计回归方法使用反演结果进行基于阈值的质量控制，其物理意义更为明确，结果更为可靠，更具有应用价值。

2 反演与质量控制方法

RSS（Remote Sensing System）公司基于SSM/I的GSW算法[5]，为AMSR-E开发了新的线性反演方法，称为多元线性回归（Multiple Linear Regression，MLR）[1]：

式中：Pj为反演所求的海洋大气参数，R为线性方程。角标i指代AMSR-E的通道（1=6.9V，2= 6.9H，…），角标j指代反演的海洋大气参数（1=TS，2=W，3=V，4=L）。

由于两个低频波段（6.9 GHz，10.7 GHz）与3个高频波段（18.7 GHz，23.8 GHz，36.5 GHz）对空气的吸收不同，因此回归方程采用如下形式：

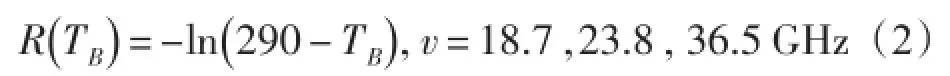
MLR算法是目前最常用的星载微波辐射计反演算法，具有结构简单计算快速的优点。但MLR算法并不具有明确的物理意义，反演结果的精度不高。国家卫星海洋应用中心（National Satellite Ocean Application Service，NSOAS）实验室基于辐射传输模型（Radiative Transfer Model，RTM）和Nelder-Mead搜索算法建立了非线性反演算法，用以解决MLR算法的不足[6]。

辐射计的观测亮温可以表达为海面温度、海面风速、水汽含量和液水含量的函数。因此，可以将观测亮温数据和大气海洋参数构建为非线性超定方程组，并使均方误差最小化，以期获得有效的大气海洋参数。

式中：ki是权重系数，表示各个观测通道的贡献程度。绝大多数情况，令ki为1或0是比较方便且合适的。MSE的物理意义也十分明确，表示反演各个通道观测亮温平均的误差偏离程度。

如果忽略辐射传输模型与真实情况之间的偏差，那么均方误差能直观的表现出反演结果的好坏：均方误差小，表示反演结果满足辐射传输模型的给定条件；反之，表示反演结果与辐射传输模型偏离较大，结果不可信。

因此，我们可以得到一种质量控制的方法。设定一个阈值，将式（4）的最小化均方误差与阈值相比较，大于该阈值的反演结果认为为不可靠结果。

3 仿真实验

对于一个系统，鲁棒性（robustness）和稳定性（steadiness）是衡量系统工作性能的重要指标[7]。鲁棒性指系统在内部结构发生扰动的情况下，外部干扰抵御能力的保持能力。在反演系统中指训练样本的改变对反演结果的影响。这对于线性反演十分关键，而非线性反演显而易见不存在鲁棒性的问题。稳定性指系统抵御外部干扰以保持理想工作状态的能力。在反演系统中可以通过对测试样本的调整考察反演系统的稳定性。

3.1 无观测噪声实验

假定观测数据不存在任何噪声的理想情况，我们已经获得了线性反演算法和非线性反演算法的反演结果（见表1）。由于线性反演引入了回归模型带来新的误差来源，因此不可避免的具有大于非线性反演的误差[8]。

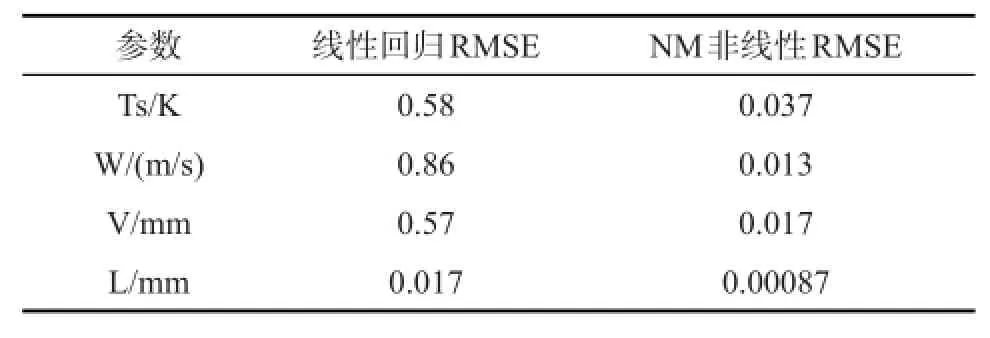
表1 线性反演和非线性反演结果

3.2 含观测噪声实验

3.2.1 数据准备

我们考虑在仿真实验中添加标准差为0.1 K的高斯分布噪声，并对实验数据的分布情况进行限定。我们建立了两组仿真数据，每一组仿真数据含有400 000个数据点，每个数据点包括海面温度（273～303 K）、海面风速（0～20 m/s）、水汽含量（0～80 mm）、液水含量（0～0.3 mm）等变量。第一组仿真数据为均匀分布（uniform distribution），即海面温度、海面风速、水汽含量、液水含量等在各自的给定范围内若区间长度相同则概率密度相同。第二组仿真数据的分布形式我们称之为自然分布（natural distribution）。我们统计了AMSR-E的2010年全年日平均三级产品中海面温度、海面风速、水汽含量、液水含量分布的概率密度。依据这样的概率密度分布，我们对仿真数据的分布进行了约束（见图1）。

3.2.2 阈值分析

实验中，我们共使用了线性反演（MLR）和非线性反演（NM）两种反演方法，均匀分布和自然分布两种数据分布形式。因此，我们共获得了4种反演结果，即：均匀分布下的线性反演，自然分布下的线性反演，均匀分布下的非线性反演，自然分布下的非线性反演。将阈值设定为从0.1至无穷大，可以得到阈值、反演结果（RMSE）、有效数据的关系。

海面温度的反演依赖于C波段数据而其余3个参数对C波段并没有这么敏感，非线性反演不同的参数还可以通过对反演波段的减少提高空间分辨率。海面温度反演需要使用微波辐射计全部波段的观测数据，因此反演结果我们以海面温度为例进行概括说明。

图1 自然分布的仿真数据

图2 阈值与反演rmse、阈值与有效数据关系

表2 反演结果与阈值

图2和表2的内容是一致的，我们分析了图2的结果并与无噪声实验进行了比较。与MLR算法的无噪声实验（rmse=0.58K）相比，噪声实验的反演结果在一个数量级（均匀分布0.79 K，自然分布0.98 K）。而NM算法对噪声十分敏感，其反演误差比无噪声实验大一个数量级（约20倍）。这也说明了NM算法的误差主要来源于仪器的观测误差，对观测仪器的改进能够极大的提高采用NM算法的反演结果精度。而MLR算法并不能将观测仪器的改进结果有效的反馈为反演数据质量的改进。从稳定性的角度出发，即NM算法稳定性差，易收到噪声干扰；MLR算法稳定性强，在复杂情况下也能保证部分反演结果可获得。

使用同一种反演方法对不同的仿真数据样本进行反演计算，反演结果的变化特征也是不同的。MLR算法对均匀分布数据的反演结果要优于自然分布数据，而NM算法对自然分布数据的反演结果要优于均匀分布数据。这是因为MLR算法在数学上是采用概率统计的方式进行回归计算，并不能体现辐射传输模型的物理过程。NM算法反演结果的变化特征符合客观认知，我们认为这是依据辐射传输模型对数据进行了有效的筛选。图2的右图也支持我们这一结论，如果按照阈值进行数据筛选，MLR算法的有效数据所剩无几。这是因为MLR算法从概率分布上对数据的反演是正确的，但物理意义并不明确。考虑到阈值的物理含义，实验中MSE超出0.3K（Pauta准则）的数据其反演结果仅仅可能在统计结果上是正确。

3.2.3 数据筛选

我们对阈值分析过程中挑选出的有效数据进行统计分析，比较MLR算法和NM算法筛选出的有效数据有何异同。由于阈值在这两种算法中的选择不尽相同，我们不考虑阈值的物理含义，直接分析了有效数据和反演结果之间的关系（见图3）。

自然分布下NM算法的反演结果始终优于MLR算法（见图3b）。无论是相同反演结果下有效数据保留的个数，还是相同有效数据下反演结果的好坏均说明了这一情况。而均匀分布下，两种算法的有效数据和反演关系曲线产生了交叉。我们参考自然分布下的曲线，选择交叉点作为阈值进行数据筛选试验。

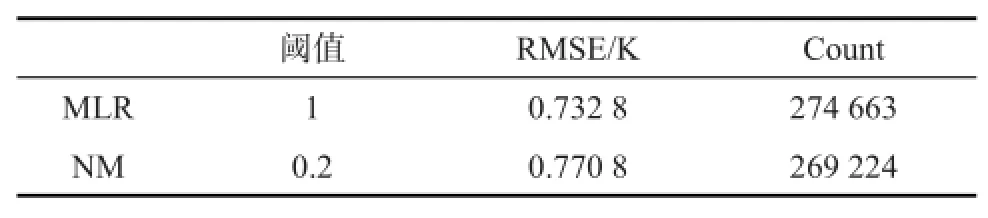
表3 阈值选取

对于均匀分布数据，MLR算法筛选后的有效数据仍然保持了近乎均匀分布的情况，只是在数据集的区间端点处分布较少。这是由于回归模型并没有添加关于区间端点的边界条件限制。以水汽反演结果为例，MLR算法的反演结果会有小于0 mm或大于80 mm的情况出现。NM算法则能够通过数据筛选，使均匀分布的海面温度和海面风速筛选后分布情况向自然分布靠拢。也就是说，在绝大多数高风速以及部分低温度情况下[9-10]，观测亮温收到很小的噪声影响都会带来辐射传输模型解的不确定性。

图3 均匀分布、自然分布下有效数据和反演结果的关系

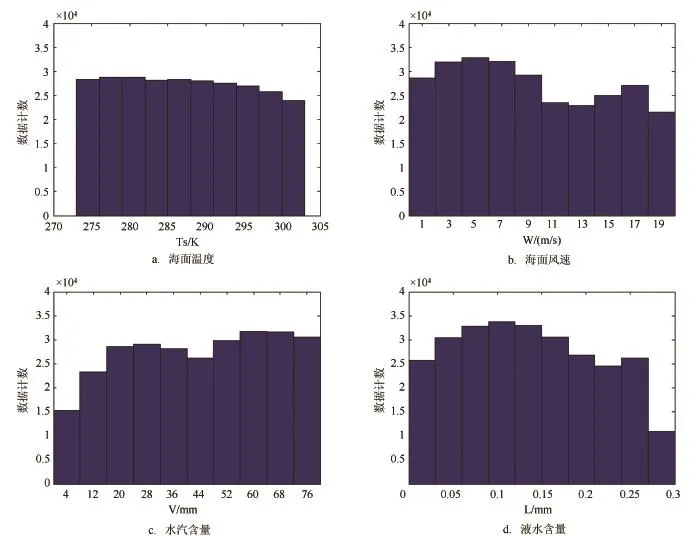
图4 MLR算法有效数据分布

图5 NM算法有效数据分布

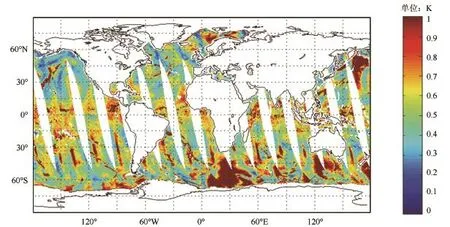
图6 AMSR-E 2010年5月1日升轨数据阈值

3.2.4 总结

通过仿真实验的分析，我们认为以MLR算法为代表的线性反演算法具有低鲁棒性，高稳定性的特点；以NM算法为代表的非线性反演算法具有高鲁棒性，低稳定性的特点。即MLR算法对反演的训练样本要求较高，NM算法具有自然而然的高鲁棒性；MLR算法在复杂情况下仍然能够获得一定的反演数据，而NM算法在复杂情况、特别是高风速情况下不能获得可靠的反演结果。在数据质量控制方面，NM算法筛选出的数据具有严格的物理含义，可靠性较强。

4 观测数据实验

根据仿真实验的情况，我们对AMSR-E 2010年5月的观测数据进行了反演处理，与浮标数据相比海面温度的RMSE为1.41K，RSS的L2b产品与浮标数据相比海面温度为1.47K。同时，我们对2010年5月1日的沿轨亮温数据进行NM算法的反演处理以及数据筛选，并对包含C波段通道的阈值、风速、液水数据进行比对分析。

图7 AMSR-E 2010年5月1日升轨数据风速

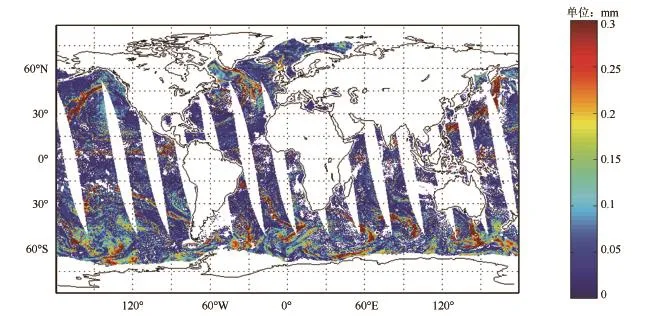
图8 AMSR-E 2010年5月1日升轨数据液水

通过对风速数据、液水数据、阈值数据的比较，我们发现降水区（即高液水区，0.18 mm以上液水可以认为有降雨）和高风速区的阈值也同样较大。例如西北太平洋日本以东洋面、东北太平洋阿留申群岛以南、赤道区域的降水区，非洲好望角以南、澳大利亚大陆以南的高风速区。这些区域的阈值较大，温度反演结果的可靠性也较差。

另一个阈值较大的区域位于南半球，在每一个观测条带都有分布，在格网投影的地图上呈椭圆状。这部分区域的观测数据受到太阳光反射的影响，被称为反辉区。这是由于AMSR-E搭载的Aqua卫星平台同时搭载了MODIS光学传感器，因此其过境时间是当地时的1300 pm，会受到太阳光照的影响。采用卫星平台和传感器的仪器参数能够计算出反辉区的区域，计算的反辉区位置在图7中有所显示（每一轨中去除的部分），与图6中阈值较大的区域较为吻合。

5 结语

我们通过仿真实验和观测数据实验，对星载微波辐射计的非线性反演算法进行了数据质量控制的能力分析，得到了满意的结果。星载微波辐射计的非线性反演算法具有物理意义明确，结果可靠的优点。这种算法在低风速、无降水区域具有较好的结果，可以筛选出高质量的大气海洋参数，并对仪器设计提出有效的建议。相比于线性反演在提高仪器的观测精度时并不能够有效的提高反演结果的精度，非线性反演能够有效的利用仪器精度提高带来的优势。卫星过境时间影响了仪器的观测覆盖，0600am和1800pm过境的卫星平台能够最大限度的提高星载微波辐射计的单轨覆盖范围，避免反辉区的影响[11]。

[1]Wentz F,Meissner T.Algorithm Theoretical Basis Document[Z].In Version:2000.

[2]李德仁,张良培,夏桂松.遥感大数据自动分析与数据挖掘[J].测绘学报,2014,43(12):1211-1216.

[3]国家卫星海洋应用中心.2014年中国海洋卫星应用报告[R].北京:国家卫星海洋应用中心,2015.

[4]JAXA A E.Data Users Handbook[Z].Saitama,Japan:JAXA Earth Observation Center,2006.

[5]Goodberlet M A,Swift C T,Wilkerson J C.Ocean Surface Wind Speed Measurements of the Special Sensor Microwave/Imager (SSM/I)[J].IEEE Transactions on Geoscience and Remote Sensing,1990,28(5):823-828.

[6]王兆徽,宋清涛,蒋兴伟,等.星载微波辐射计的非线性反演算法[J].高技术通讯,2015,(4):376-383.

[7]Dorf R C,Bishop R H.Modern Control Systems[M].Reading, Mass.:Addison-Wesley,1998:580.

[8]王兆徽,刘宇昕,宋清涛,等.星载微波辐射计的线性与非线性反演算法比较[J].航天器工程,2015,24(4):130-135.

[9]Stammer D,Wentz F,Gentemann C.Validation of Microwave Sea SurfaceTemperatureMeasurementsforClimatePurposes[J]. Journal of Climate,2003,16(1):73-87.

[10]Meissner T,Wentz F J.The Complex Dielectric Constant of Pure and Sea Water from Microwave Satellite Observations[J].IEEE Transactions on Geoscience and Remote Sensing,2004,42(9): 1836-1849.

[11]蒋兴伟,林明森,宋清涛.海洋二号卫星主被动微波遥感探测技术研究[J].中国工程科学,2013,15(7):4-11.

Data quality control based on nonlinear retrieve algorithm of spaceborne microwave radiometer

WANG Zhao-hui1,2，LIU Wei1,3，ZHANG Qiong-xiong4，SONG Qing-tao1,2

（1.Key Laboratory of Space Ocean Remote Sensing and Application,SOA,Beijing 100081 China;2.National Satellite Ocean Application Service,Beijing 100081 China;3.Senior High School of Zhuanghe City,Dalian 146400 China;4.Suixi Meteorological Administration, Zhanjiang 524300 China）

Based on the oceanic and atmospheric parameters retrieve processing of spaceborne mircrowave radiometer,quality control in linear and nonlinear retrieve algorithm is analyzed by using simulation experiment seperately.The results of nonlinear retrieve of AMSR-E data are used to verify the conclusion of the simulation experiment.The experiments indicate that the nonlinear retrieve algorithm has definite physical meanings, reliable results,better data quality control,and application potential.

spaceborne microwave radiometer；nonlinear retrieve algorithm；data quality control；sea surface temperature

P731.11

A

1003-0239（2017）01-0025-09

10.11737/j.issn.1003-0239.2017.01.004

2016-09-19；

2016-10-23。

国家自然科学基金面上项目（41276019，41076012）；国家海洋局海洋公益性行业科研专项（201305032）；国家自然科学基金面上项目（41276019，41076012）。

王兆徽（1989-），男，研究实习员，硕士，主要从事微波遥感研究。E-mail:wzh@mail.nsoas.org.cn

宋清涛（1971-），男，研究员，博士，主要从事海洋遥感研究。E-mail:qsong@mail.nsoas.org.cn