建材装备制造业原材料采购供应商选择评价研究

许 磊，郭顺生，胡烈锋，朱泽强，陈龙龙

(武汉理工大学 机电工程学院，湖北 武汉 430070)

随着我国经济改革逐步进入深水区，建材装备制造业实现了跨越式发展，整体呈现健康、快速、良性的发展态势，极大地拉动了地区经济发展水平。在激烈的竞争环境下，建材装备制造业凸显出以下特点：上下游产业关联密切，产品具有小批量、多品种的特点，个性化需求越来越强；其所涉及的产品工程复杂，生产周期长，需要配备大量的外购件，该产业对资源的消耗和依赖很大，采购部采购的原材料或者半成品质量甚至直接影响最后产品成型的质量，因此企业对原材料采购供应商、物流厂商等相关合作商提出了更高质量的要求[1]。

在如何帮助企业控制产品原材料质量，合理选择优质供应商这个问题上众多学者和专家们都有着深入的研究。耿秀丽、叶春明[2]在研究传统供货商评价指标分配权重时存在主观性的问题，采用改进粗糙集来挖掘指标信息，用加权求和法分配权重，对于不确定的指标信息运用直觉模糊集来处理，最后通过VIKOR方法对供货商进行合理选择。梁智昊、何维达[3]利用粒子群算法训练BP神经算法的权值和阈值来加快神经网络的收敛性，提出了一种由主成分分析法、BP神经算法和粒子群算法相结合的神经融合法，并用实例验证了供应商选择的合理性和有效性。 王建廷、余强[4]针对多条供应链的供应商选择进行研究，提出ANP和PROMETHEE结合法，ANP方法解决评价指标相互依存、反支配作用的问题，PROMETHEE在做评价时具有非补偿性的优点，出现逆序的问题最少，最后通过实例验证其合理性。马琳[5]针对电梯供应商的选择问题，将熵权和TOPSIS方法结合建立一种供应商评价模型，利用熵权的思想确定最优权重配置，弥补之前供应商评价模型主观性过强的缺点，并用实例加以验证模型的可行性。Tavana[6]等提出了基于ANN和自适应人工神经模糊法相结合的供应选择模型框架，先把数据聚合再进行层次分析，最后的排名和选择根据多层选择器来综合得出。

这些研究虽然深入，但不同方法的针对性、适用范围和企业可操作性都不同，尤其对于建材装备制造企业原材料采购供应商有其特有的指标准则，研究甚少。目前企业在原材料采购供货商方面主要存在的问题是面对繁多的供货商缺乏科学系统的选择方法、潜在供应商优势开发不足、交易投入人力、物力、信息费用成本高和供需双方信息反馈不及时等。

笔者在以上学者的研究基础上，结合建材装备制造业的独特性，首先创建原材料采购供应商评价指标体系，确保准确完整地体现供应商的综合实力，接着用层次分析法ANP分析得出不同级别的指标权重，用Levenberg-Marquard算法创建神经网络供应商评价模型，通过采集到的供应商的实际原始数据，训练得到合适的评价模型，最后用实际供应商数据来测试、验证模型的可行性和合理性。

1 原材料供应商评价指标体系的创建

1.1 原材料采购供应商评价体系建立的原则

建材装备制造业配件供应商指标选择原则不只是一般的采购供应商的评价指标，在选择指标时应充分考虑到建材装备制造业的行业特点，如“小批量、多品种”产品模式，个性化和多样化越来越突出，产业之间关联效应强；同时建材装备制造业产品复杂、产业链长、原材料工艺和品种要求高等特点。在选择评价指标时需要遵循以下原则：①系统全面性原则；②简明科学性原则；③拓展性原则；④可行性原则。

1.2 原材料采购供应商评价方法的选择

随着供应商选择评价的深入研究和交叉学科的兴起，运筹学、数学、神经网络、计算机科学等相继被应用到评价方法中，其中有层次分析法、模糊综合评价法、TOPSIS评价法、遗传算法、灰色关联度评价法和BP神经网络算法。模糊综合评价法对含有模糊性的信息资料进行准确、合理的评价，但计算过程复杂多变，分析权重时主观性比较强；TOPSIS评价法适用范围广，直观性强，可靠性高，但是存在实际应用中会遇到“逆序问题”的出现，常需要与其他方法配合使用，难度高；遗传算法全局搜索能力强，在适用空间内可快速搜索全局最优解，但容易早熟，由于遗传算法属于随机类算法，稳定性不高等。

综上所述，各种方法都存在一定的优缺点和适用范围。近年来随着人工神经网络的迅速发展，BP神经网络具有较强的非线性映射能力、较强的自学习自适应性能力、泛化能力和容错性强等优点，在模式识别、 非线性逼近、评价预测等方面均取得良好的效果。但也存在一些缺点，如容易陷入局部最优解、收敛速度慢等问题，因此笔者采用优化后的BP神经网络算法——Levenberg-Marquard算法来构建原材料采购供应商评价模型。

1.3 原材料采购供应商评价指标确定

根据评价指标的原则，经过详细了解建材装备制造企业合作的采购供应商信息，表1列出了供应商的8个一级指标，23个二级指标，并分别对每个指标都进行了详细的解释。

表1 原材料采购供应商评价指标汇总表

2 BP神经网络简介及原材料采购供应商评价模型设计

2.1 BP神经网络基本原理

BP神经网络是一种误差可逆传播算法大量训练出来的多层前馈网络，包括前端输入层、中间隐含层和输出层3层结构，如图1所示。BP神经网络在没有事先了解输入输出内部映射关系情况下可使用最速下降法学习和存储这种关系量，在反向传播过程中随时调整各网络层的连接权值和阈值以达到误差平方和最小的目的[7]。

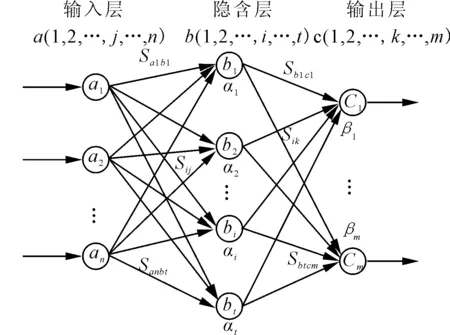
图1 BP神经网络结构图

如图1所示，BP神经网络用于原材料采购供应商评价的基本思路如下：设输入变量X=(a1,a2,a3,…，an)，隐含层变量Y=(b1,b2,b3,…，bt)，输出层变量Z=(c1,c2,c3,…，cm)，期望输出变量P=(p1,p2,p3,…，pm)，α(1,2,3,…，t)是隐含层t个节点的阈值，β(1,2,3，…,m)是输出层m个节点的阈值，Sij是输入层和隐含层之间的连接权值，Sik是隐含层和输出层之间的连接权值，δ和ψ是隐含层和输出层的激励函数。

BP神经网络算法存在学习效率低、收敛慢、局部极小等缺点，LMBP算法是牛顿法和梯度下降法的结合，是BP神经网络算法的改进算法，它的优势在于连接收敛速度快、精度高，因此笔者将采用Levenberg-Marquardt算法对原材料采购供应商做出评价。

LMBP算法原理[8]如下：假设某次修正的权值时的误差函数是E(s)，现在神经网络的权值是s(k)，目的修改量为Δs(k)，desk是信号从隐含层到输出层第k个节点的输出，则下一刻修改后的权值为：

s(k+1)=s(k)+Δs(k)

(1)

BP神经网络算法的实际误差为：

(2)

其中：

eq=Pqk-desqk

(3)

根据牛顿法，对下一刻的误差函数展开二阶泰勒级数后可得:

s(k+1)=s(k)+A-1h·CTk

(4)

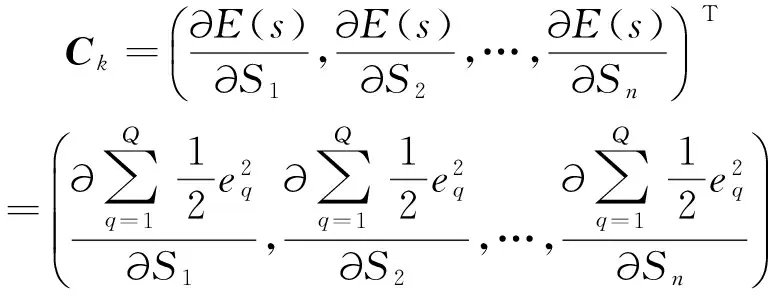
(5)

其中Hk为LMBP算法引进的Jacobian矩阵：

e=[e1,e2,…,eQ]

(6)

Hessian矩阵Ah单个元素表示为：

(7)

把Hk带入式(7)可得：

(8)

其中

(9)

当误差函数值E(s)在最低处时，θ会变得很小甚至可忽略不计，这样式(8)可简化为：

(10)

将式(10)带入式(4)中化简得：

(11)

(12)

式中：I为单位矩阵，σ是很小的正数，故

(13)

2.2 BP神经网络设计参数选择

表1中原材料采购供应商评价体系中共有23个指标，因此神经网络的输入层节点为23。输出层节点个数是按照评价模型的输出结果数来定，这里只输出一个最终评价值，因此输出层节点数为1。隐含层节点数一般是通过经验公式来确定。经验公式[9]如下：

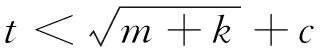
式中：t为隐含层节点个数，m为输入层节点数，k为输出层节点数，c为1～10之间的常数。笔者首先通过以上公式得到隐含层节点的最小值和最大值，在这个范围内通过试错法来测试误差最小的节点数为10。隐含层的激活函数选双正切函数tansig函数，考虑到输出层输出结果值在0到1范围内，因此输出层的激活函数选用Log-Sigmoid函数。神经网络具体参数如表2所示。

表2 神经网络参数表

3 实例分析

唐山建材装备制造A公司与尼日利亚合作关于生产辅料侧式取料机(REB)的“尼日利亚(EDO)”项目，其中需要采购一台规格为YOX450的液力耦合器，经查询公司供应商管理系统以及联系采购部、质量部、市场部的有关人员筛选出供应商库中售卖此种型号液力耦合器的18个供应商，并根据表1所示的评价指标收集到的原始数据记录在表3中。

表3 供应商各参数指标原始记录表

表3中P1,P2,…,P18为18个供应商的编号，由于采集到的各指标数值差距大，量纲也各不相同，因此首先需要对数据进行归一化，笔者将表中原始数据归一化为[0,1]范围的数，归一化方法有很多，这里采用最大最小法，这样线性变换处理后可保留数据原始价值，不会丢失潜在信息。归一化公式如下：

(14)

式中，X(i)为任意输入归一化后的值；x(min),x(max)为原始记录表中最小、最大值。在表3中，最后一行“归一化分值”栏中数值和实际供应商评价等级对应关系如表4所示，Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ级依次代表着供应商综合实力从最弱到最强；表3中倒数第二行“综合评分”栏是根据层次分析法(AHP)[10]计算出一级、二级指标的所有权重后和原始数据相乘得到的结果。

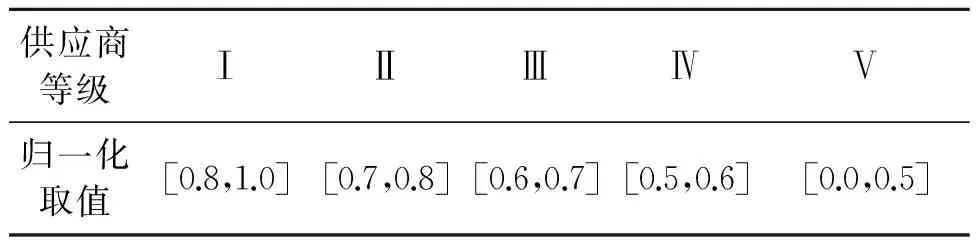
表4 供应商等级和归一化数值对应表

样本归一化处理后就可以作为输入向量参与训练，笔者采用MATLAB工具箱中newff函数创建一个神经网络，trainlm作为训练函数，sim函数作为仿真函数。表3中共18组数据，用前14组作为训练数据，后4组数据做仿真预测。

神经网络经过16次训练误差已达到最小0.000 1，其训练过程误差曲线如图2所示，期望输出值和实际输出值误差曲线如图3所示，从图3可以看出训练样本的网络实际输出值和预期输出值拟合度很高，训练好的神经网络可以准确评价供应商综合等级。

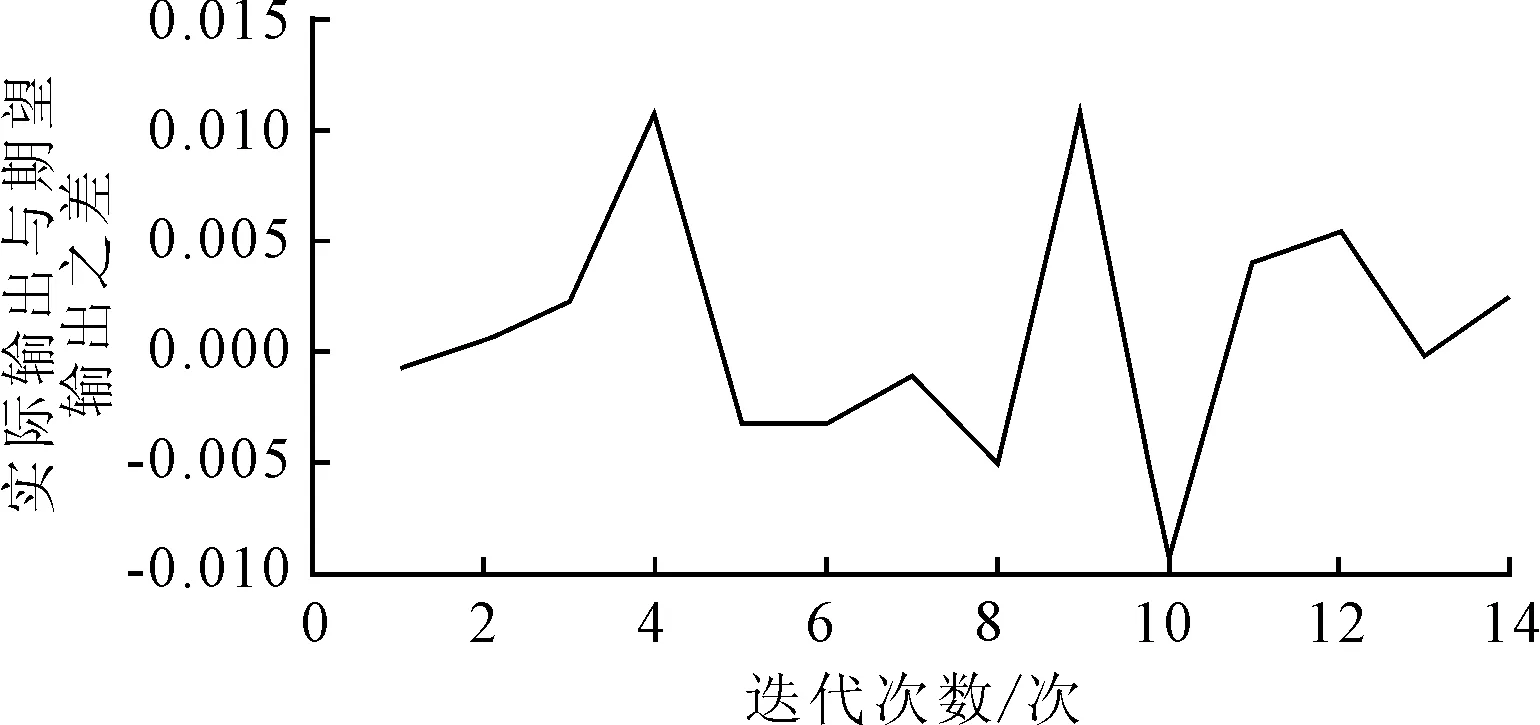
图2 网络的训练过程误差曲线(trainlm函数)

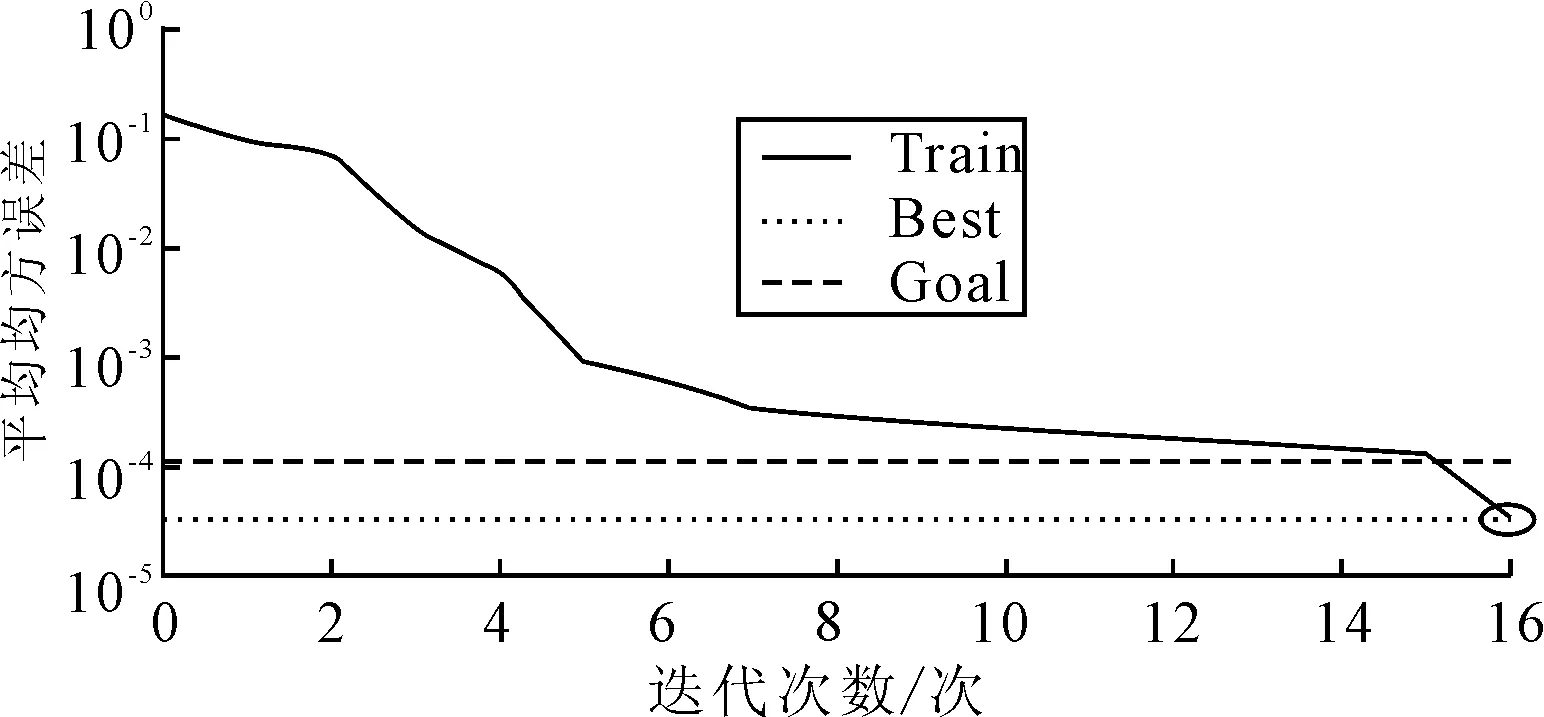
图3 期望值和实际输出误差曲线图(trainlm函数)

表5列出14个供应商经过训练后神经网络实际输出值和期望输出值的对比记录，从表5中可以看出P1,P2，…，P14的实际输出值和期望输出值最大误差为0.010 9，与优秀等级完全一致，因此该模型训练结果满意。

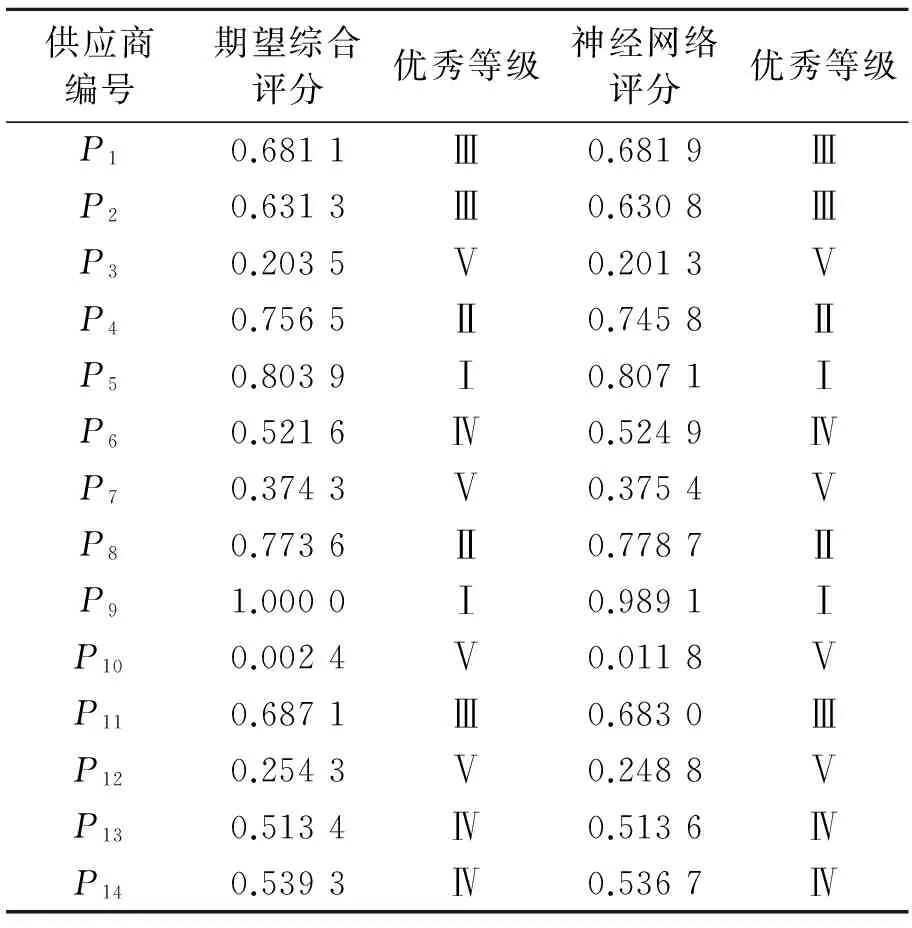
表5 训练供应商实际评分和网络评分对比表

为了更好地测试该神经网络模型的评价准确性，用表3中的后4个供应商作为测试数据，测试结果与实际评价对比如表6所示。

表6 测试供应商实际评分和网络评分对比表

从表6可知：实际综合评分和网络评分分值非常接近，误差在可接受范围内，对判断一个供应商的等级和综合分值提供了准确的数据参考，从而更好地对原材料质量进行控制。因此笔者采用Levenberg-Marquardt算法创建的神经网络评价模型对原材料采购供应商的选择结果是科学、合理的。

4 结论

在建材装备制造业中，企业项目接近70%的成本花在原材料采购方面，面对市场上参差不齐的供应商，一种科学、合理的供应商选择评价方法至关重要。笔者在研究建材装备制造行业供应商的特点后，针对性地创建了供应商评价体系，并收集指标数据信息，在归一化处理之后用于神经网络的训练，训练函数选择Levenberg-Marquardt算法中的trainlm函数，通过训练结果得出训练样本的网络实际输出值和期望输出值吻合度很高，并准确地给出了供应商评价结果。

为了测试trainlm函数对神经网络收敛速度和误差精度的影响，用BP神经网络算法的常用traingd和traincgf训练函数作对比分析，结果显示了trainlm函数在收敛速度和误差精度控制上更优秀，最后用新的供应商测试数据验证该模型的合理性和准确性，数据结果表明，该模型可以准确给出供应商综合评价分值和优秀等级参考值。该模型为建材装备制造企业优选供应商提供了理论依据，从而也加强了企业对产品原材料质量的控制，减少了成本。

[1] 马斌，孙利波，张旭，等.建材装备集团化制造企业采购管理策略研究与系统应用[J].工程管理,2007(1)：79-83.

[2] 耿秀丽,叶春明.基于直觉模糊VIKOR的服务供应商评价方法[J].工业工程与管理,2004(3):22-29.

[3] 梁智昊,何维达.基于神经网络融合技术的供应商评价研究[J].管理科学,2015(24):1-9.

[4] 王建廷，余强.多条绿色建筑供应链下供应商的选择分析——基于ANP-PROMETHEE模型[J].建设经济与管理,2016(6):27-32.

[5] 马琳.基于战略物料优化的电梯供应商评价选择研究[D].天津：天津工业大学,2016.

[6] Tavana M.A Hybrid Intelligent Fuzzy Predictive Model with Simulation for Supplier Evaluation and Selection[J].Expert Systems with Application,2016,61:129-144.

[7] Ismail A, Jeng D S, Zhang L L.An Optimised Product-unit Neural Network with a Novel PSO-BP Hybrid Training Algorithm: Applications to Load-deformation Analysis of Axially Loaded Piles[J].Engineering Applications of Artificial Intelligence,2013,26:2305-2314.

[8] Javed Iqbal,Asif Iqbal,Muhammad Arif. Levenberg-Marquardt Method for Solving Systems of Absolute Value Equations[J].Journal of Computational and Applied Mathematics,2015,282:134-138.

[9] 王冰，郭东强.基于BP神经网络的企业内部知识转移绩效综合评价研究[J].情报科学，2016(1)：141-146.

[10] 李勇，何蕾，庞传军，等.基于层次分析法的火电厂运行情况量化评价方法[J].电网技术，2015(2):500-504.