基于刚柔耦合模型的副车架尺寸优化

吴 波，陈 博

(武汉理工大学 机电工程学院，湖北 武汉 430070 )

悬架作为车身与车轮之间的弹性连接，应具有传递载荷、缓和冲击、衰减振动的作用，其结构大体可分为弹性元件、减振装置和导向机构三大部分[1]。悬架总成装配图如图1所示。

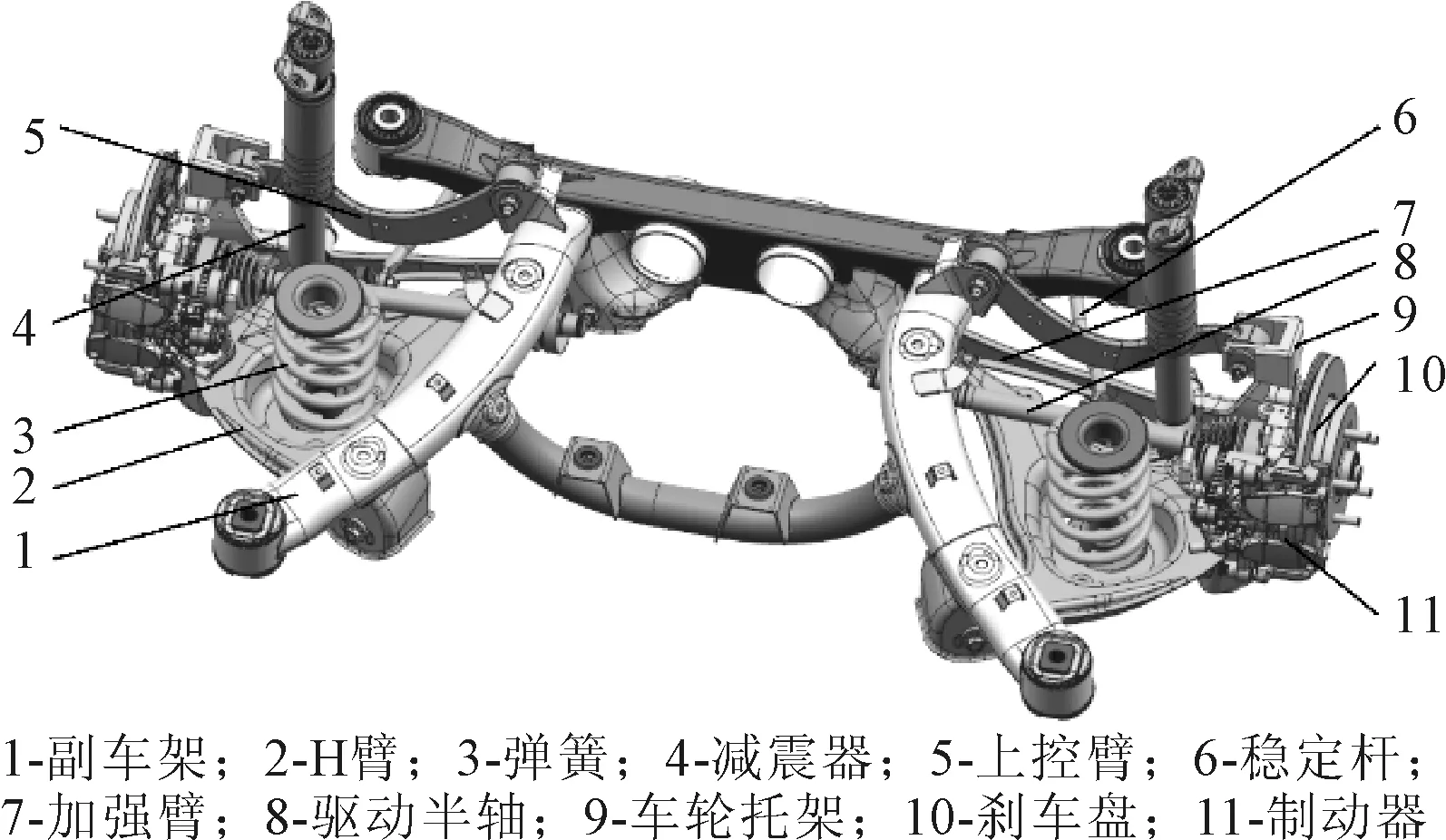
图1 悬架总成装配图

副车架是悬架总成中十分重要的一个构件，悬架的其他构件基本上都通过副车架与车身相连，副车架的出现使得悬架从散件集合成为一个总成，可进行平台性开发，且使悬架连接刚度得到改善，进一步衰减振动提高舒适程度，但安装副车架会增加整车的质量。因此，对副车架进行尺寸优化研究显得尤为重要。笔者针对某品牌跨界车的双横臂后独立悬架建立ADAMS/CAR刚柔耦合动力学模型，根据三种典型工况对副车架的受载情况进行仿真并提取载荷数据，并运用OptiStruct同时考虑三种工况的受力情况对副车架进行尺寸优化。

1 ADAMS/CAR刚柔耦合模型的建立

1.1 刚柔耦合动力学基本原理

构件通过运动副相互连接形成的机械系统模型称为多体动力学模型，传统的刚体动力学模型将每个构件视为刚体，不考虑构件的变形。这种方法忽略了变形对结构整体性能的影响，故在考虑分析对象变形的情况下，将其柔性化处理后导入动力学模型中，可建立刚柔耦合的动力学模型。

刚柔耦合的基本思想是通过模态展开法，用模态向量和模态坐标的线性组合来表示弹性位移，并计算每一时刻的弹性位移来描述对象的变形[2-3]。

笔者结合Hypermesh有限元软件[4]对副车架进行柔性化处理，形成模态中性文件，导入ADAMS/CAR中建立副车架柔性化的刚柔耦合悬架动力学模型[5-6]。

1.2 副车架的有限元模型

副车架的有限元模型如图2所示。在通过UG模型导入Hypermesh中建立有限元模型时，模型均为实体，考虑后续尺寸优化所需，应将模型进行参数化处理。此处可通过Hypermesh中的抽取中面功能，将3D实体单元转换为2D壳单元并划分网格，厚度将作为壳单元的一个属性变量，从而完成模型的参数化处理。

图2 副车架有限元模型

网格划分完成后，有限元模型包含423 263个节点、259 267个单元。副车架的材料为Q345，其密度为7.85 g/cm3，泊松比为0.28，弹性模量为206 GPa，屈服极限为345 MPa。根据副车架的有限元模型，可创建ADAMS/CAR能够识别的MNF中性文件，该过程需对副车架进行自由模态分析，副车架前6阶模态很小，在此计算前12阶模态。表1为副车架7～12阶模态频率。

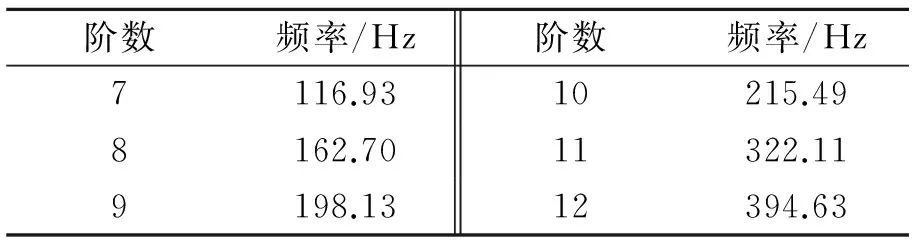
表1 副车架自由模态频率

1.3 刚柔耦合动力学模型的建立

首先，根据悬架的三维数模确定各硬点位置的坐标，并以此建立悬架子系统和稳定杆子系统，此时各构件均当作刚体处理，所建模型为多刚体动力学模型。然后，通过副车架有限元模型生成的MNF文件替换掉刚体的副车架模型，建立刚柔耦合的悬架模型。最后，将刚柔耦合的悬架子系统、稳定杆子系统和实验平台组合成悬架总成的刚柔耦合模型，如图3所示。该模型为后续虚拟工况仿真并提取副车架载荷奠定了基础。

图3 刚柔耦合悬架总成虚拟样机

2 副车架载荷提取与静力分析

汽车在行驶过程中，其受载情况十分复杂，多数情况为动载荷。而在分析汽车底盘零部件的静力学问题时，由于其实际受力的复杂性，可以通过其实际受载情况进行虚拟工况的定义，再通过动力学模型的仿真获得零部件的受力，从而对副车架进行静力学分析。选取倒车制动、单轮跳动和右转这三种典型工况进行分析，采用准静载仿真法提取后副车架上各硬点位置所受载荷。这种方法计算结果准确，可行性高，是汽车底盘零件静应力分析的常用方法。

2.1 三种典型工况下副车架的受载情况

在动力学仿真获得后副车架的硬点受力时，需要通过计算得到虚拟样机试验所需的载荷输入，即车轮轮心的受力情况。考虑到三种典型工况受力时均为瞬时冲击，运用静平衡法近似计算轮心受力并不合理。若运用动量守恒定律，其作用时间、冲击速度都无法求得。在结合公司大量的试验数据和经验总结后，此处采用公司所提供的经验公式进行计算，如式(1)所示。计算时，坐标系与ADAMS坐标系相同，即以汽车倒退方向为X的正方向，以车身侧向向右的方向为Y的正方向，以垂直地面向上的方向为Z的正方向。

(1)

式中：FXR、FYR、FZR为后车轮X、Y、Z方向所受的力；ax、ay、az为对应工况X、Y、Z方向的加速度；Msf为满载时后悬架簧载质量，为978.07kg；Muf为满载时后悬架非簧载质量，为136.93kg。对应工况的加速度值如表2所示。其中的具体参数来源于公司制定的设计标准。

表2 典型工况分析加速度

根据工况受力特点与经验公式，计算各工况所受的力及硬点位置载荷。

(1)倒车制动工况

在倒车制动工况下左右两轮受载相同，主要受纵向力与垂向力作用。轮心纵向力FXR=3 354.8 N，垂向力FZR=5 463.5 N。

(2)单轮跳动工况(左轮跳动)

在左轮跳动工况下左轮载荷应大于右轮载荷，主要受垂向力作用。左轮的垂向力FZR-L=9 057.9 N，右轮的垂向力FZR-R=4 792.5 N。

(3)右转工况

右转工况下悬架左侧受压，左右两轮侧向力相同，左轮垂向力应大于右轮垂向力。左右两轮侧向力FYR=2 396.3 N，左轮垂向力FZR-L=5 463.5 N，右轮垂向力FZR-R=4 792.5 N。

由计算的轮心载荷，根据所建刚柔耦合模型通过静态载荷将计算结果作为载荷激励输入，创建三种典型工况的模拟试验台，提取副车架各连接硬点位置上的力与力矩，如表3～表5所示。

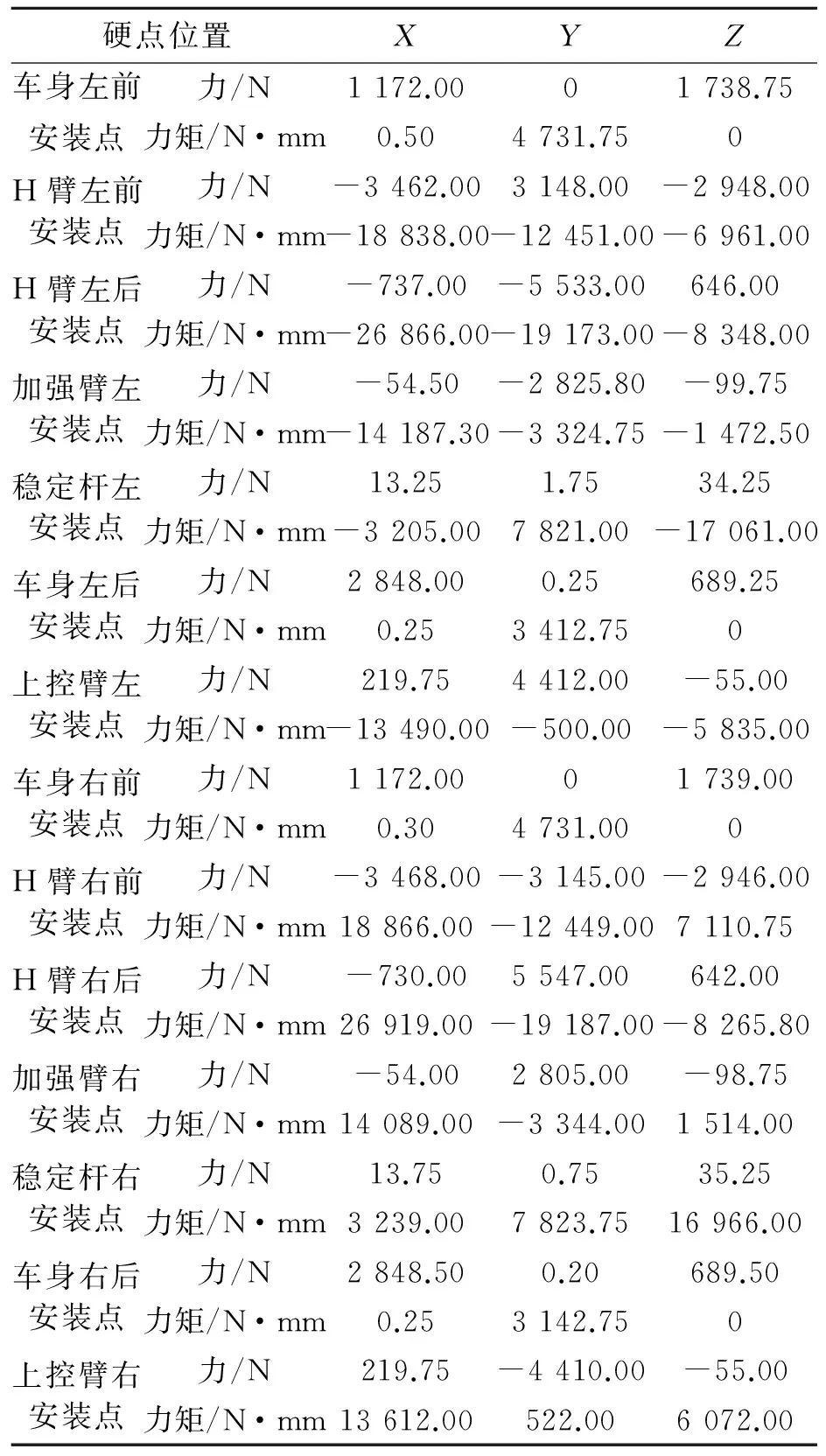
表3 副车架倒车制动工况硬点位置载荷

2.2 副车架静力学分析

机械零件的静力学计算是其结构优化的前提，应力应变的大小、分布将直接决定结构优化的优化余量与可行性。对于悬架零件的静力分析，需要注意其约束的设置。

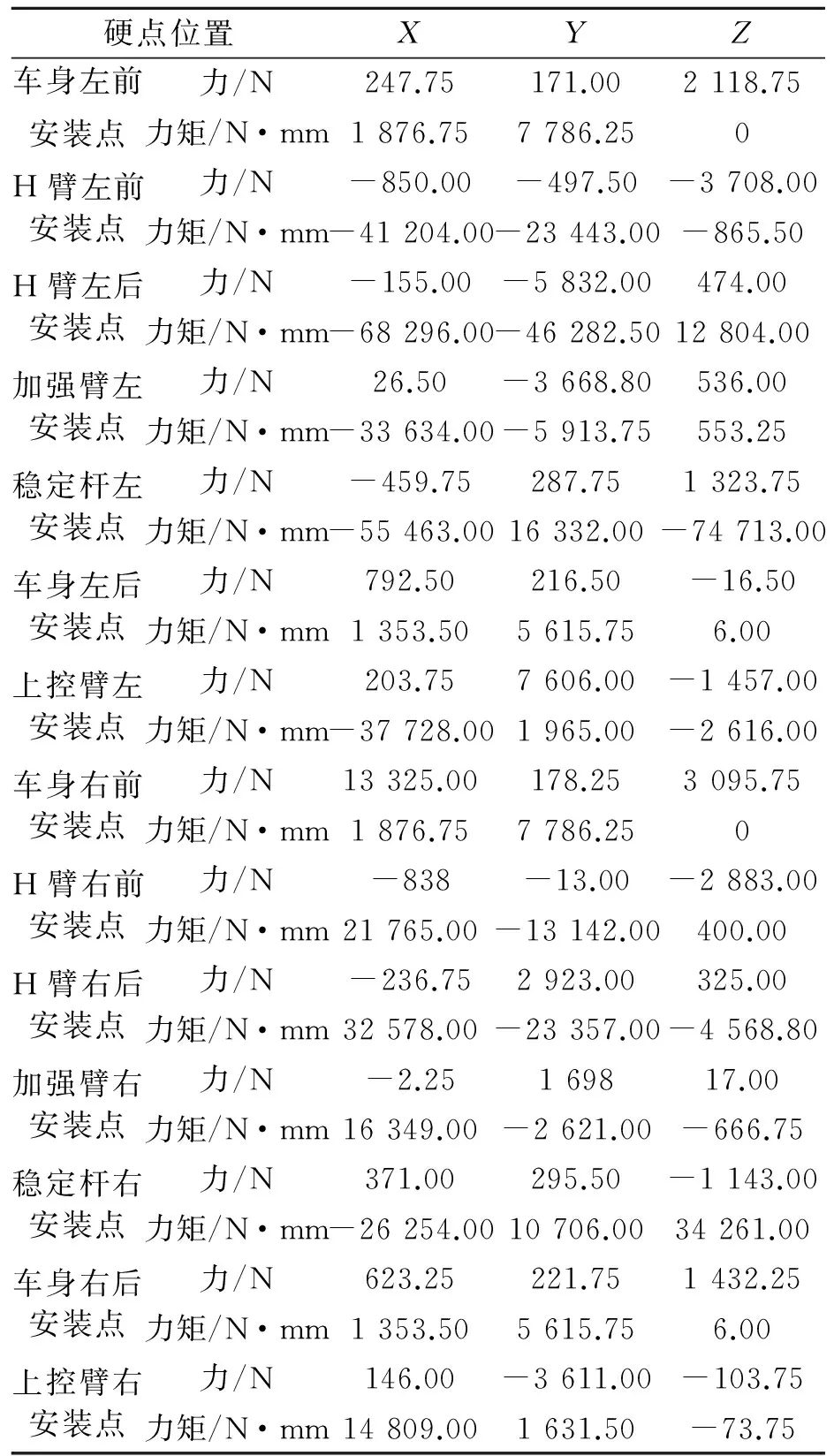
表4 副车架单轮跳动工况硬点位置载荷

悬架的构件与构件之间通过衬套相连，而衬套的存在则导致零部件在约束点可以进行一定程度的偏移或扭转。而且对于汽车底盘零件来说，不存在完全固定的连接点，原因是车辆整体在行驶时具有加速度，整体都会运动，那么将副车架与车身的连接点固定死的约束方法并不符合实际情况。此处应采用惯性释放法对其进行约束。

惯性释放法是一种可以对分析对象不作约束处理进行静力分析的方法。其基本原理是通过分析对象的惯性(质量)力来平衡外力。在分析时，会约束一个节点位置的6个自由度作为一个虚支架，同时通过计算外力作用下每个节点在每个方向上的加速度，从而转换成惯性力施加在每个节点上，达到力系平衡的目的。图4～图9为后副车架在三种典型工况下的应力与应变图。

倒车制动工况下最大应力为171.9 MPa，最大应力位于左侧纵臂靠近上控制臂连接件的位置。最大位移量为1.294 mm，且位于副车架左侧的前安装点位置附近。

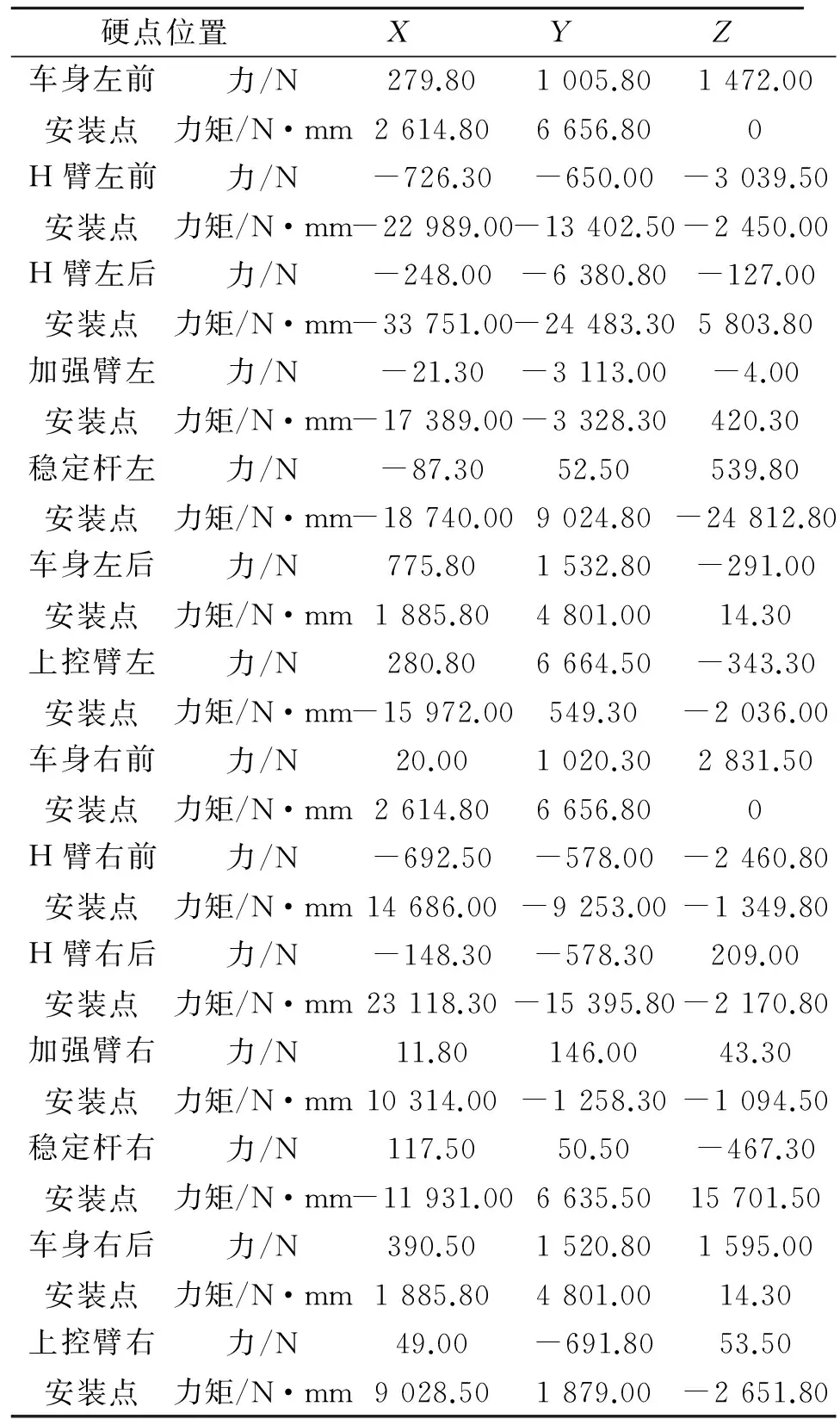
表5 副车架右转工况硬点位置载荷

图4 倒车制动工况应力云图

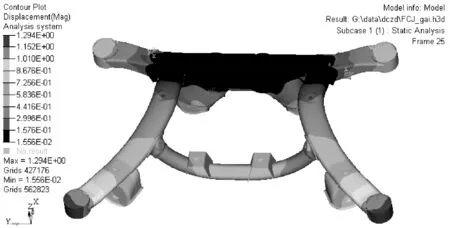
图5 倒车制动工况应变云图

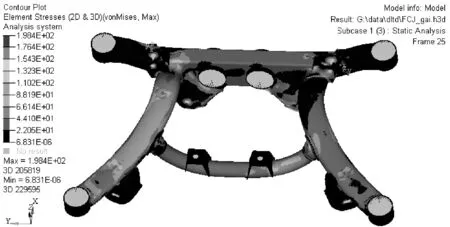
图6 单轮跳动工况应力云图

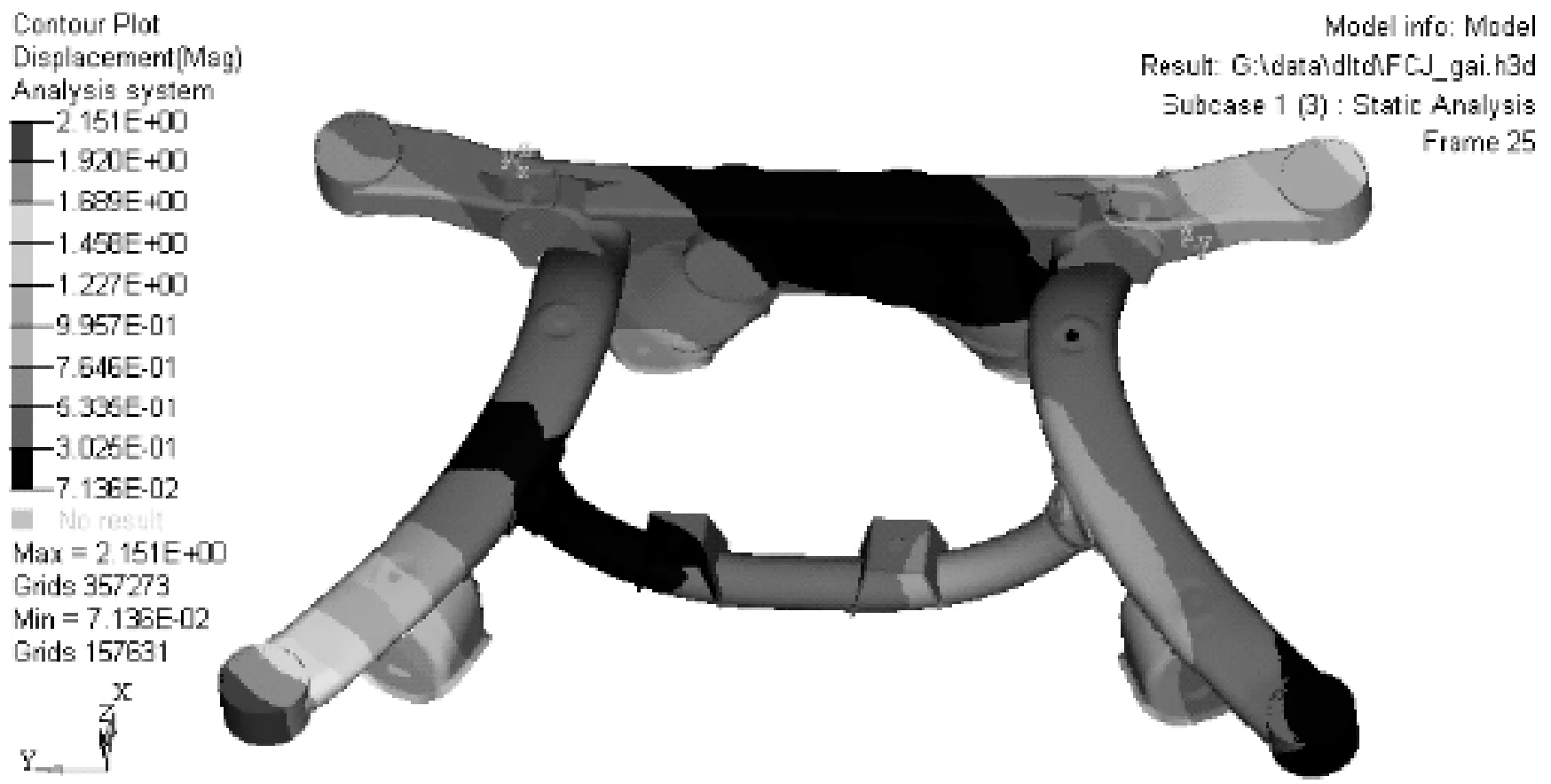
图7 单轮跳动工况应变云图

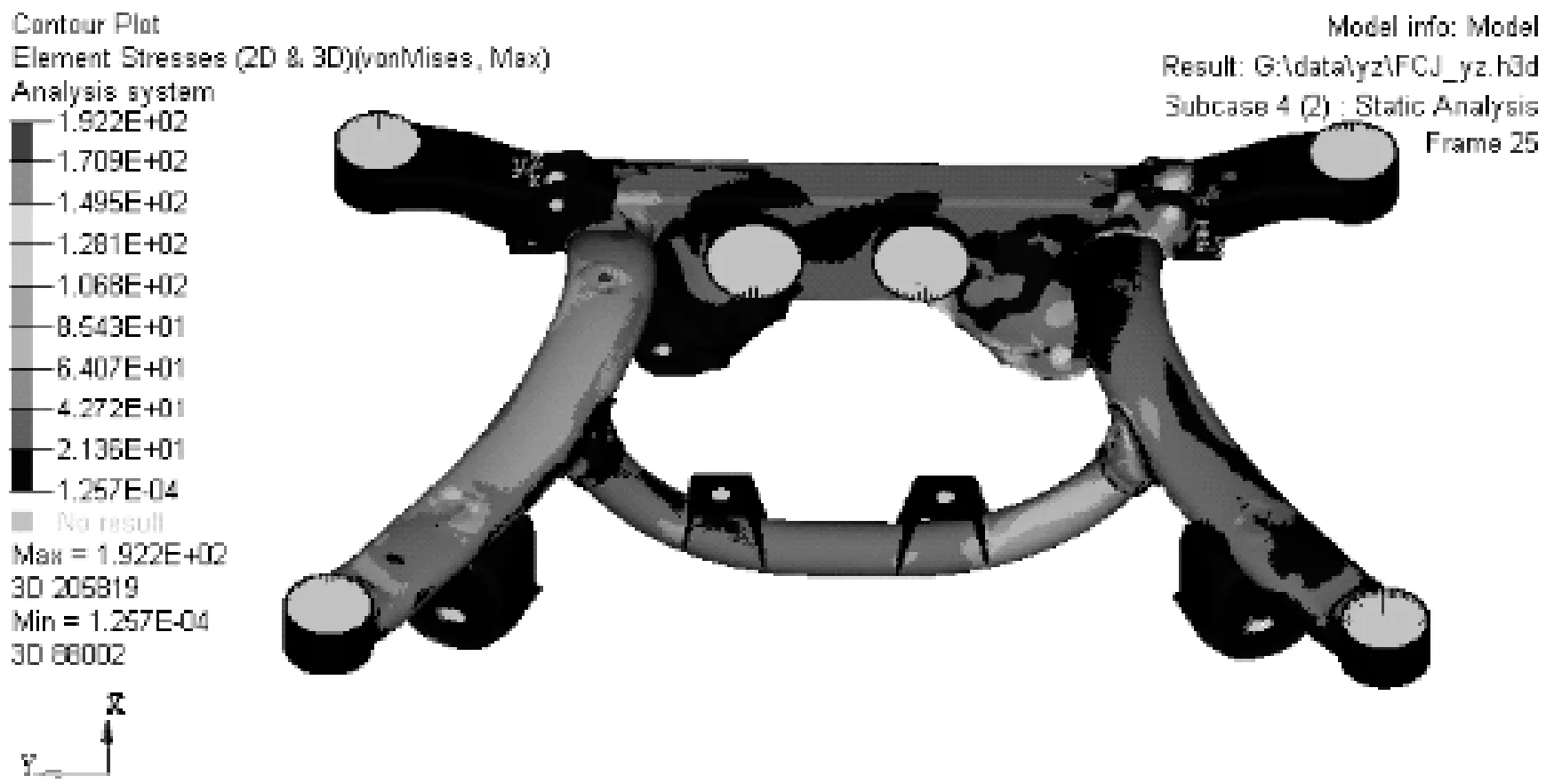
图8 右转工况应力云图

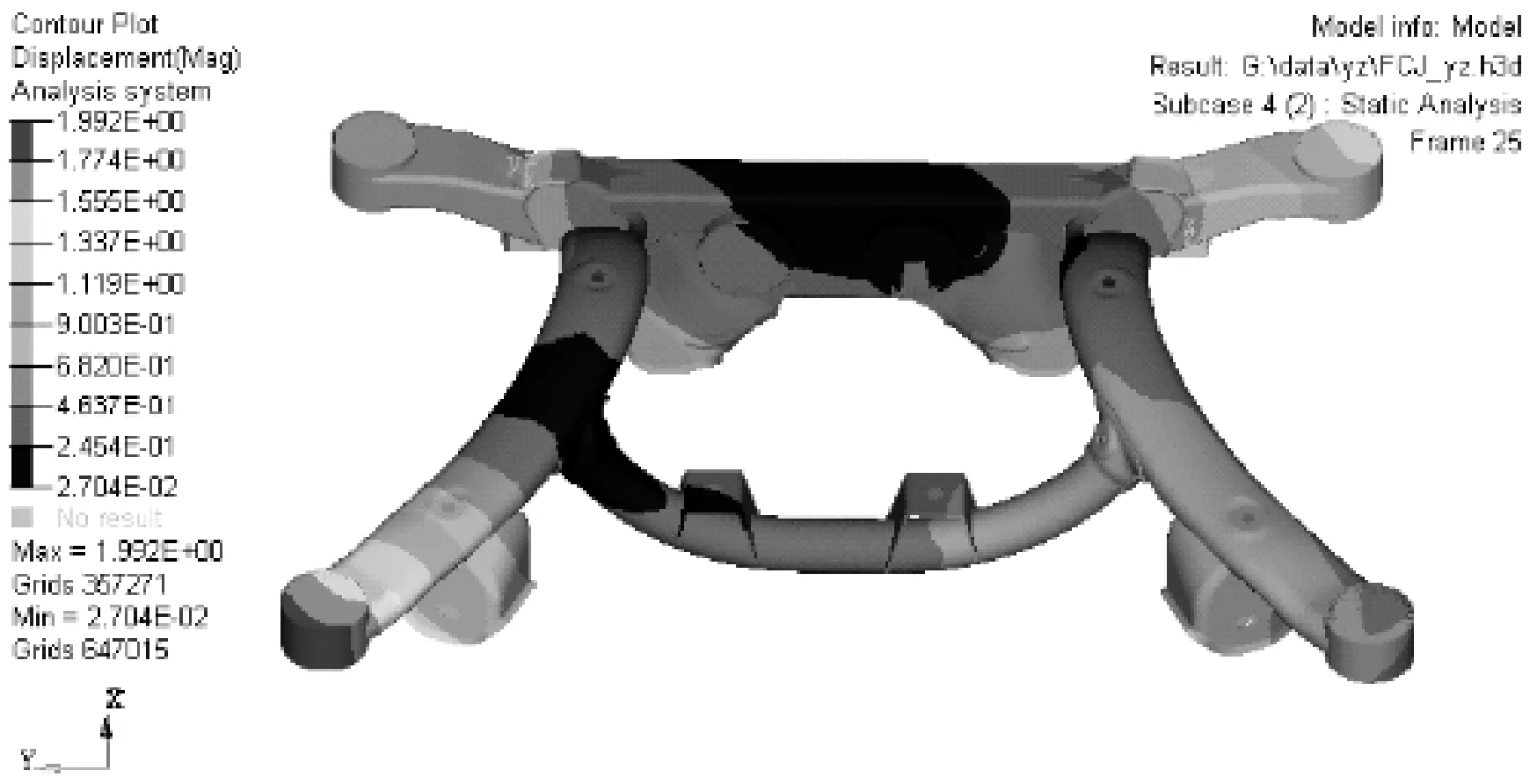
图9 右转工况应变云图

单轮跳动工况下的最大应力为198.4 MPa，最大应力位于左侧上控制臂连接件的焊接位置。最大位移量为2.151 mm，且位于后副车架右侧的前安装点位置附近。

右转工况下的最大应力为192.2 MPa，最大应力位于左侧上控制臂上。最大位移量为1.992 mm，且位于后副车架右侧的前安装点位置附近。

副车架的材料为Q345，其许用应力为345 MPa，三种工况分析结果表明，副车架还有较多的优化空间。

3 基于OptiStruct的副车架尺寸优化

尺寸优化是在已有的结构、材料和受力情况的基础上对结构截面尺寸，如梁单元的横截面积、壳单元的单元厚度等进行优化设计。尺寸优化在工程中运用较多，是一种比较成熟的优化方法[7-9]。笔者将同时考虑三种典型工况的受力，对副车架进行尺寸优化。

3.1 优化模型的建立

3.1.1 设计变量

所研究的副车架，其基本结构由两个纵臂、一个前横臂和一个后横臂组合而成，考虑到目标车型是前置后驱的跨界车，后副车架的后横臂具有主减速器的支撑功能，且结构复杂、厚度不均匀，此处仅考虑两个纵臂和前横臂的厚度尺寸优化，即选取前横臂厚度和纵臂厚度的作为设计变量。

3.1.2 目标函数

针对副车架的尺寸优化其主要目的是为了轻量化设计，对于目标函数的选定应选取后副车架整体质量作为目标函数。

3.1.3 约束条件

约束条件的确定，可考虑工件的应力、应变和频率等性能。副车架的刚度要求一般在悬架整体刚度上考虑，且结合这种结构的副车架结构形式，当满足应力要求时，其刚度一般也满足要求。基于此情况，在此仅考虑三种工况的极限应力，对应力进行约束，并取1.2的安全系数作为应力值的上限，应力应在287.5 MPa内。

根据以上结构优化三要素的选取，建立如下所示的优化模型。

目标函数：minmass(t)

设计变量：tLow1≤t1≤tUp1tLow2≤t2≤tUp2

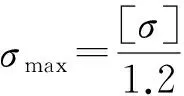
式中：mass(t)为副车架的总质量，t1、t2为前横臂和纵臂的厚度，上角标Low、Up表示设计变量的下限值和上限值，σmax为有限元分析中的节点最大的Von Mises应力，[σ]为Q345的许用应力345 MPa。

为保证仿真结果的准确性，且考虑板厚设计变化范围的合理性，取板厚上下浮动值为1 mm。设计变量板厚的初始值与上下限如表6所示。

表6 设计变量厚度取值范围

3.2 优化结果

在定义优化后，选用Optistruct求解器进行优化计算[10]。目标函数的迭代过程曲线如图10所示。表7为尺寸优化结果对比。

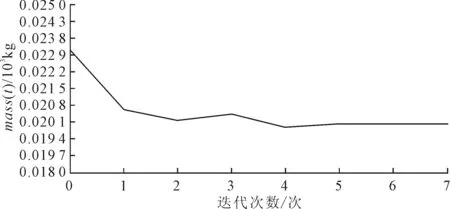
图10 尺寸优化目标函数迭代计算曲线图

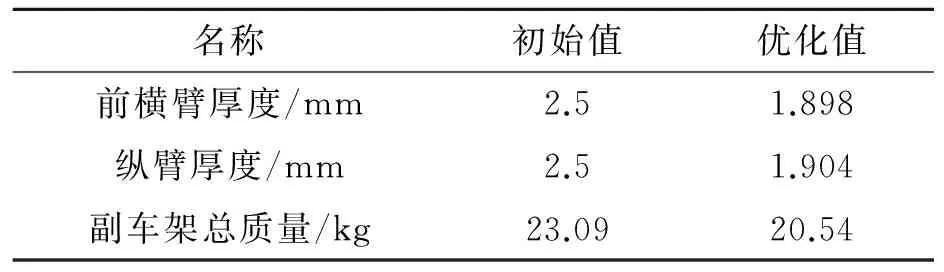
名称初始值优化值前横臂厚度/mm2.51.898纵臂厚度/mm2.51.904副车架总质量/kg23.0920.54

尺寸优化后，前横臂厚度由2.5 mm优化至1.898 mm，纵臂厚度由2.5 mm优化至1.904 mm，副车架整体质量减轻3.38 kg。

3.3 结果验证与对比

针对通过尺寸优化后的副车架，建立新的有限元模型进行结果验证。静力分析结果如表8所示，模态分析结果如表9所示。

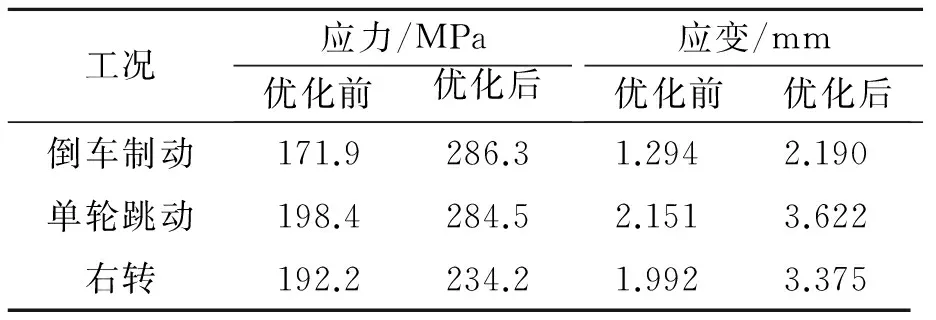
表8 尺寸优化后应力与应变变化统计表

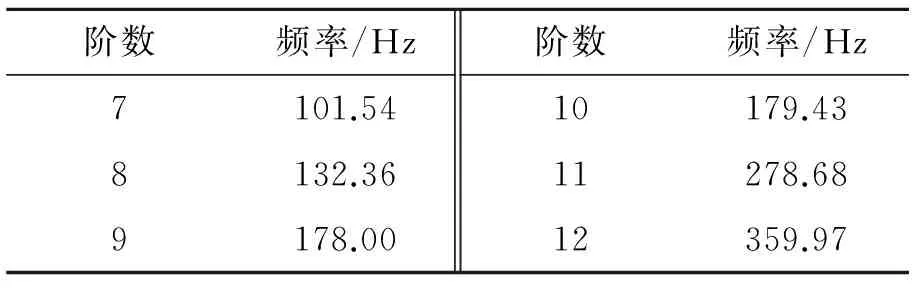
表9 尺寸优化后前12阶自由模态频率

通过静力分析可以看出，由于有应力上限作为约束条件，优化后应力不会超过上限值，取安全系数为1.2，保证了优化后最大应变量变化不大，仍然满足使用要求。

通过自由模态分析可以看出，优化后副车架的各阶频率均避开路面激励，保证了优化后的副车架不会发生共振，有良好的动态性能。

4 优化结果对悬架性能影响分析

考虑优化所带来的簧载质量变化与后副车架刚度变化对悬架性能的影响，运用刚柔耦合模型可分析柔性体变化的特点，重新建立优化后的刚柔耦合模型，并对影响悬架平顺性、侧倾性能及车轮定位的参数进行对比仿真，以验证优化结果的可行性。对比结果如图11～15所示。

图11 悬架刚度随轮跳变化对比图

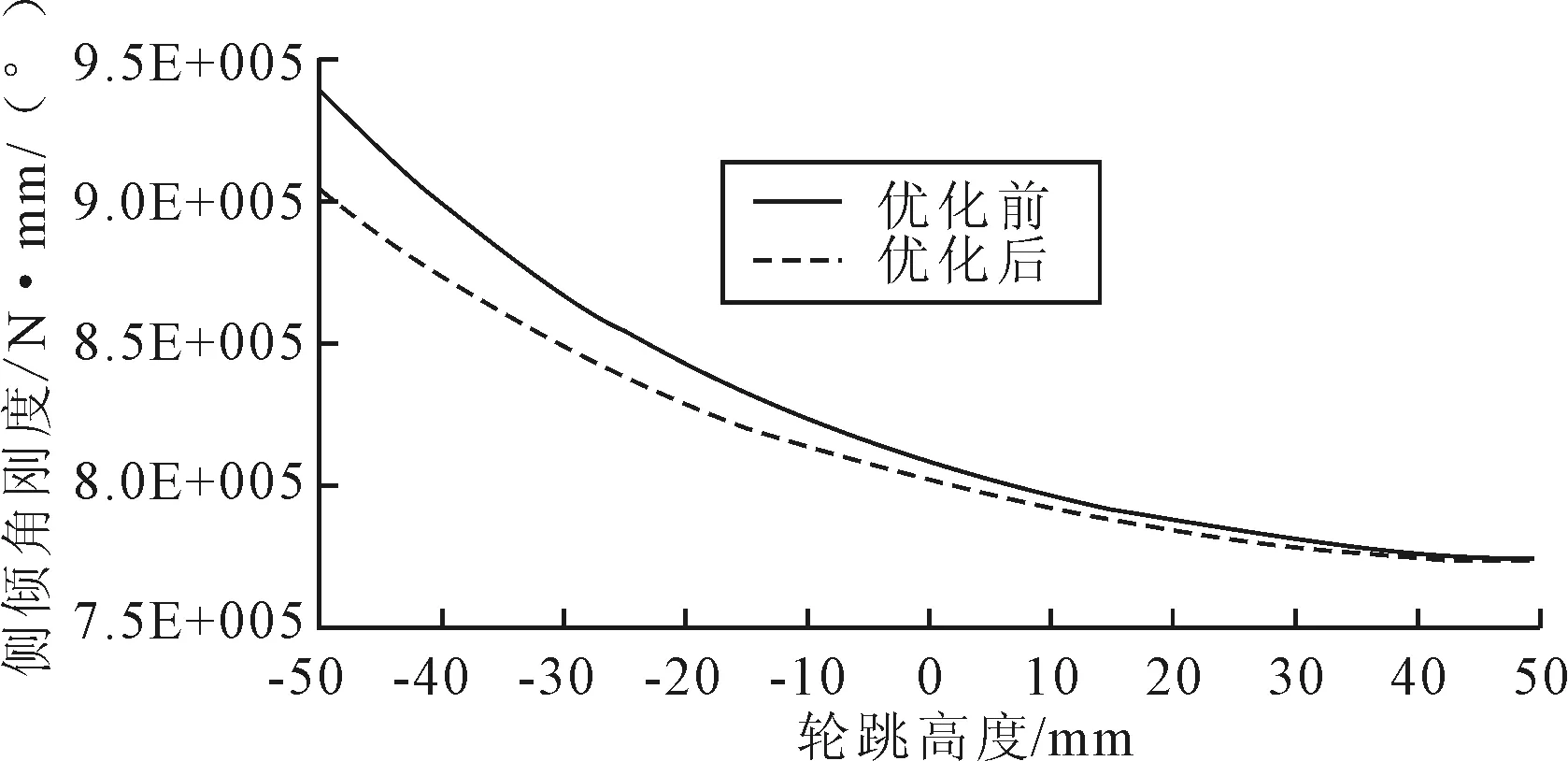
图12 侧倾角刚度随轮跳变化对比图

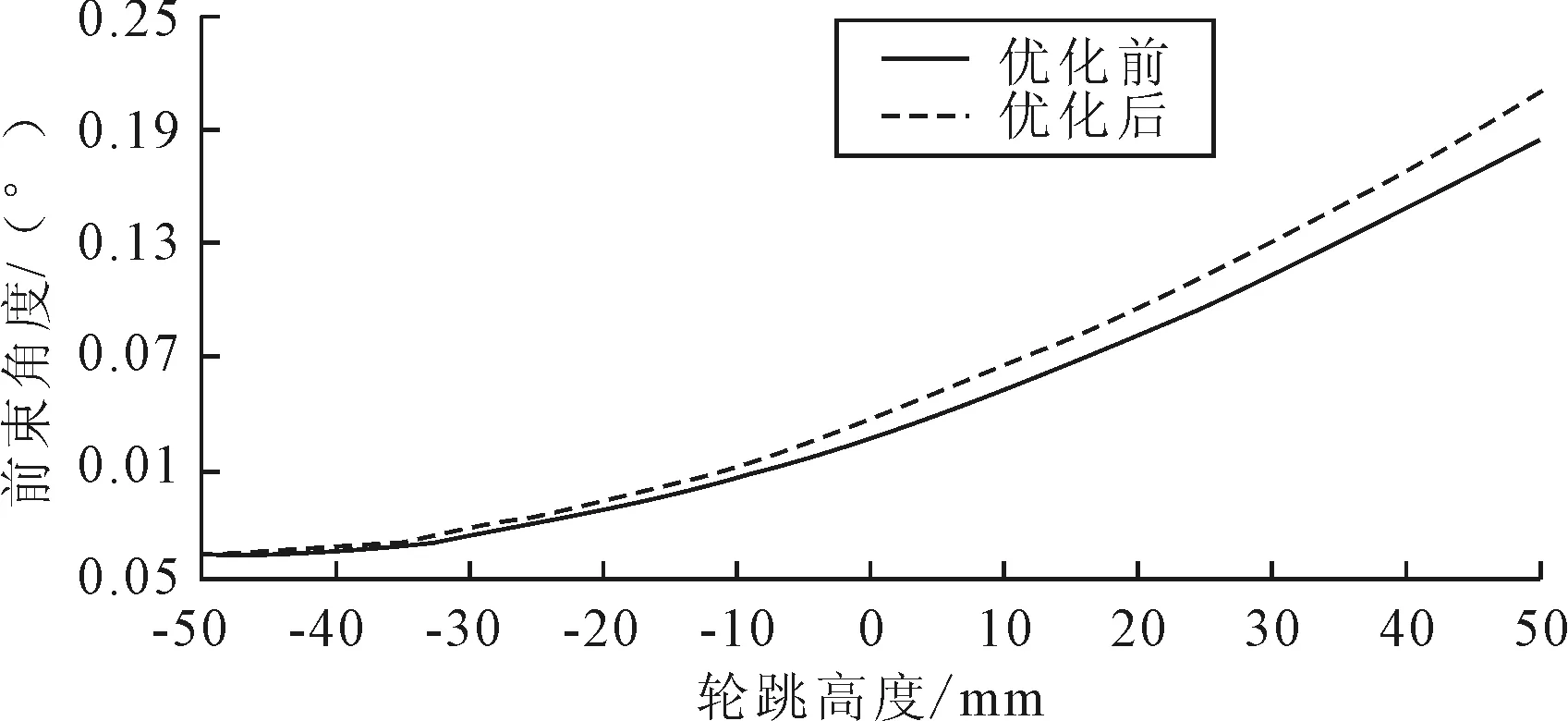
图13 前束角随轮跳变化对比图

图14 外倾角随轮跳变化对比图

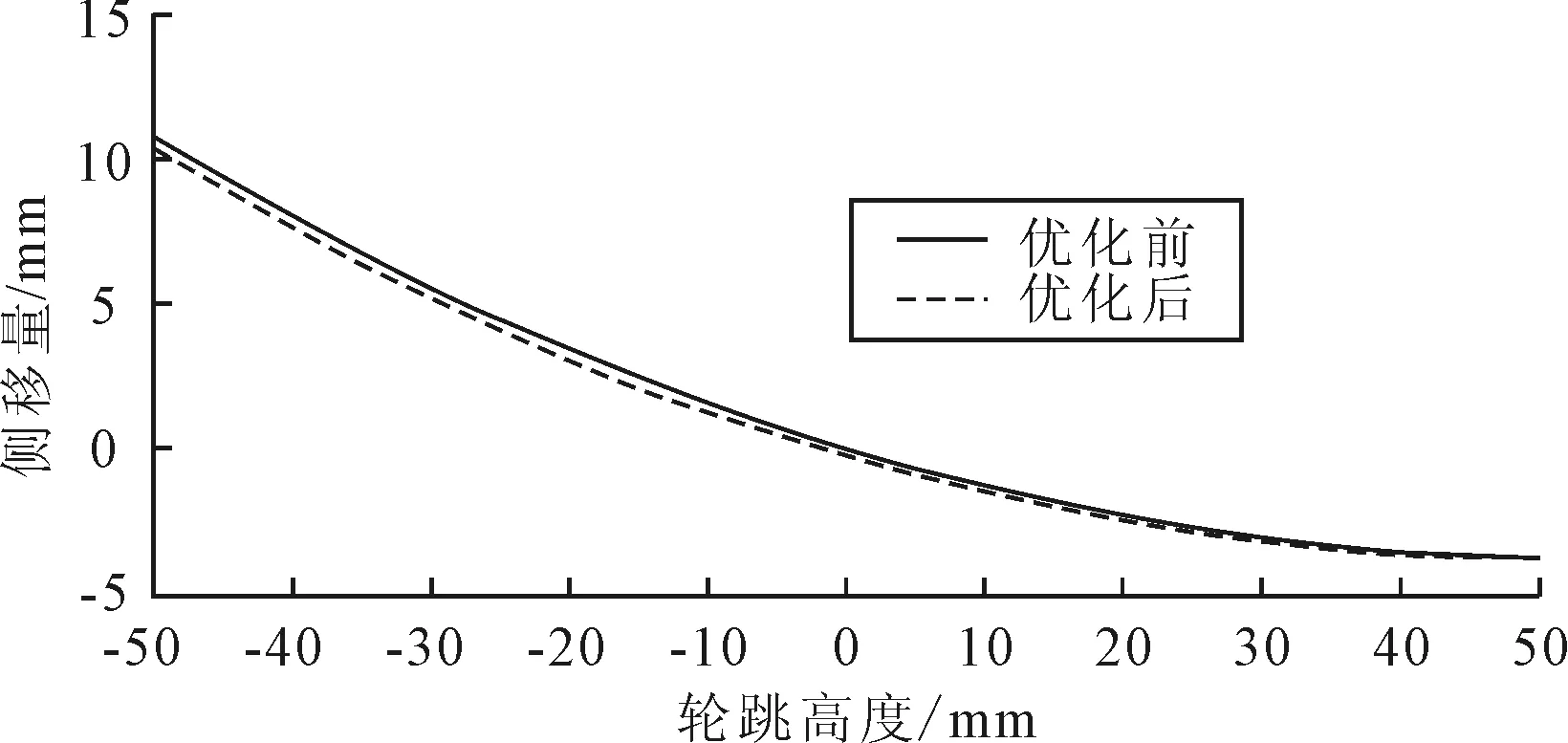
图15 车轮侧移量随轮跳变化对比图

图11～图15分别为优化前后刚度、侧倾角刚度、前束角、外倾角及车轮侧移量的对比结果。由图中可以看出，悬架刚度在优化后整体有所减小，轮跳为0时减小仅0.5 N/mm；侧倾角刚度整体变化趋势在优化前后基本一致，在轮跳为0时仅减小8 N·m/(°)；前束角在轮跳50 mm处仅增大0.03°；外倾角在优化前后的变化曲线基本一致，优化后的外倾角在数值上稍稍减少；车轮侧移量在车轮下跳50 mm时有少量减小，上跳50 mm时基本一致，优化前后的整体变化趋势基本相同。

结果表明，悬架特性参数由于副车架结构变化均有少量降低，但仍满足使用要求，优化结果得以进一步验证。

5 结论

通过对副车架的柔性化处理，运用ADAMS/CAR建立双横臂式后独立悬架的刚柔耦合动力学模型，以更接近实际情况的仿真方法提取了副车架三种典型工况的受力。建立了尺寸优化的优化模型，对副车架前横臂与纵臂进行了轻量化设计，质量减少3.38 kg,较优化前减重11.04%。通过静力学与模态分析验证了优化结果的正确性，保证优化后应力没有超过许用应力，动态性能良好。最后通过建立优化后的刚柔耦合模型，对比分析了副车架结构变化对悬架性能的影响，保证了优化结果的可行性。

[1] 刘惟信.汽车设计[M].北京：清华大学出版社，2001.

[2] 赵亮,刘艳华.基于刚柔耦合的汽车多连杆后悬架性能分析[J].汽车实用技术,2013(10):15-18.

[3] 吕振华, 徐建国.五连杆悬架的刚体运动学和弹性运动学分析[J].汽车技术,2002(11):10-14.

[4] 李楚琳,张胜兰,冯樱.HyperWorks分析应用实例[M].北京：机械工业出版社,2008.

[5] 郭延辉,秦彦斌.基于ADAMS的客车独立悬架的运动仿真[J].客车技术与研究, 2010,32(6):5-7.

[6] 刑艺文，王东方，王燕.基于HyperWorks与ADAMS/Car联合仿真的后副车架轻量化研究[J].现代制造工程，2016(7)：76-80.

[7] 陈猛.轿车副车架设计与优化[D].合肥：合肥工业大学,2010.

[8] 梁礼光.轿车后副车架减重优化设计方法研究及应用[D].广州：华南理工大学,2014.

[9] Liao J, Shan L, Feng Y. The Design and Size Optimization of the New FCEV Subframe Based on Hypermesh Platform[J]. Advanced Materials Research, 2011,328：435-440.

[10] 殷梅,王成龙.基于Optistruct的某副车架尺寸优化设计[J].汽车实用技术,2015(4):51-54.