基于多特征融合的GA-SVM齿轮故障诊断方法

赵 国，李益兵，谢春启

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.上汽通用五菱汽车股份有限公司 技术中心，广西 柳州 545007)

根据研究表明[1]，齿轮箱的故障中，60%以上都是由齿轮引起的，而其中90%的故障都是局部故障，如点蚀、磨损和断齿等。齿轮箱处于各种复杂的环境下运行，且往往也是密闭运行。齿轮发生故障时不易发现，如果发生故障会导致生产运输延迟，生产效率变低，甚至还会导致严重的伤亡和财产损失。利用故障诊断技术能够监控齿轮的运行状态，减少系统大范围的维护以及拆箱检查带来的不便。还可以合理安排维护时间，降低维修成本，避免经济损失，提高生产效率。

目前，常用的齿轮箱故障诊断方法有小波分析[2]、希尔伯特-Huang变换[3]、经验模态分解[4]等。刘石等在小波变换、全息谱等先进故障诊断技术方面做了许多研究[5]；罗荣等将改进冗余小波包应用在齿轮箱故障诊断中，取得了良好效果[6]；Peng等在小波变换理论研究及转子碰摩故障诊断技术等方面取得了很多突破[7]；袁静[8]、WANG[9]等对采用多小波变换、双数复小波变换等离散小波变换在故障特征提取中的应用技术进行了总结。WANG等[10]提出了一种自适应的小波分析对瞬态特征的提取方面进行了研究，对连续小波变换的波形进行优化。申中杰等[11]提出了一种基于多特征和多变量的支持向量机剩余寿命预估方法。钱士才和孙宇昕利用SVM(Support Vector Machine,支持向量机)在智能检测方面进行了大量试验研究[12]；郭远晶[13]利用角域振动信号提取故障特征向量的方法，使用算法来优化SVM中的惩罚参数和RBF核函数的宽度，实现对风电齿轮箱支持向量机智能故障诊断。以上研究采用不同方法在故障特征提取和故障诊断中均取得了良好效果。但针对齿轮的故障诊断，将多特征融合应用在齿轮故障诊断上的研究比较少，联合使用遗传算法(Genetic Algorithm,GA)对支持向量机的参数优化更是不多。

笔者针对齿轮的故障特点，在小波包分解和支持向量机的基础上，提出了多特征融合的GA-SVM故障诊断方法。先对齿轮箱的原始振动信号进行三层分解，通过建立不同故障和不同频段特征信号的对应关系，并利用各节点小波系数初步分析诊断出故障原因。然后融合了峰值、方差、峭度、裕度指标等时域统计特征，进行归一化处理后，提取特征向量。最后，将其输入到遗传算法优化的支持向量机中进行诊断。实验结果表明，多特征融合的特征向量输入到遗传算法优化后的支持向量机中，可有效提高齿轮的故障诊断准确率。

1 构建特征向量

1.1 时域统计特征参数

时域统计特征是判断齿轮运行状态最简单、最直观的方法。峰值可以体现波形是否有冲击，方差可以体现信号的离散程度，峭度指标可以反映振动信号偏离正态分布程度，裕度指标可以表示信号与干扰的比值大小[14]。

1.2 小波包分解及时频域特征参数

时域统计特征参数虽然在一定程度上能表征齿轮的运行状态，但是故障齿轮的振动信号往往具有非平稳特性，因此采用小波包分解的方法在时频域进一步提取齿轮的故障特征。与小波变换相比，小波包变换不仅对低频部分进行分解，还对高频部分也进行再分解[15]。同时，小波包分解能根据振动信号的特性和分析要求，可以自适应地选择相应频带与信号频谱。三层小波包分解如图1所示。

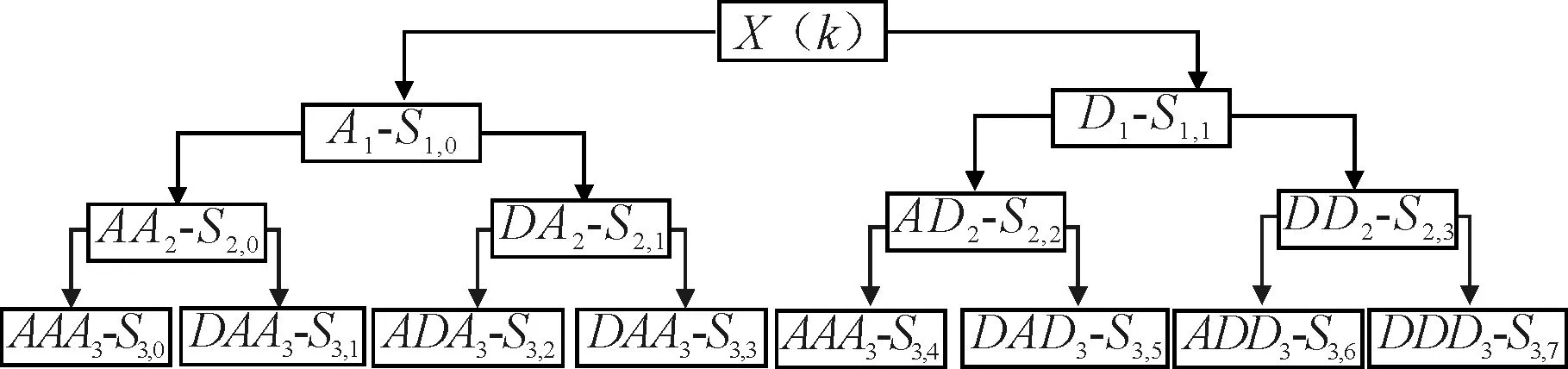
图1 三层小波包分解

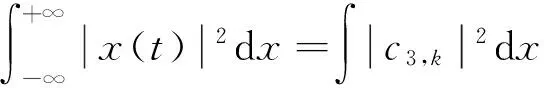
文中对小波相似和细节系数进行分析，得到初步差异效果。使用db5小波进行分解，得到并对第三层各节点小波系数重构，计算出各频段能量值。通过故障与正常齿轮的能量值对比分析，分析小波包分解的有效性。然后选取第三层各个频段的小波包能量以及第三层各个节点小波包分解系数的最大值，再融合4个时域统计特征参数，归一化处理后，提取出20维特征向量。

2 遗传算法优化支持向量机

2.1 支持向量机

支持向量机是20世纪九十年代Vapnik[16]根据统计学习理论中结构风险最小化理论提出的一种分类算法，其基本思想通过核函数将低维线性不可分问题映射到高维空间，然后在高维空间寻找最优分类超平面。将要解决的问题转化为凸二次规划问题，很好地解决了小样本、非线性问题。凸二次规划问题求解的目标分别为：最大化间隔和最小化错分程度。将两者综合为一个目标函数，需要引入惩罚参数c来权衡两者的重要程度。

支持向量机在给设样本集为(xi,yi),i=1,2,3,…，n，xi∈Rm,yi∈(1,-1)，其中xi为类属性，yi为类标记，n为数据个数，支持向量机将低维空间的输入映射到高维空间，寻找最优超平面，其超平面定义如下[17]：

(1)

式中：ai为拉格朗日乘子；K(x,xi)为核函数；b为偏置。

本文选用高斯径向核函数为：

(2)

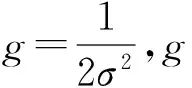
当惩罚参数越大，越不能容忍出现误差；惩罚参数越小，越欠拟合。无论过大过小，都将使其泛化能力差。当核函数参数越大，支持向量越少；核函数参数越小，支持向量越多。因此，如何需要选取合适的参数是关键。相比传统方法依靠经验选择参数，网格寻优、PSO寻优、交叉验证法等方法都有着或多或少的缺点。笔者利用遗传算法优化支持向量机对齿轮的故障进行识别、诊断，建立支持向量机模型。使用遗传算法进行惩罚参数c和核函数参数g的寻优，寻找测试集以及预测集误差最小的那一组进行仿真分类，有效地提高了分类的准确率。

2.2 遗传算法优化支持向量机

遗传算法是一种借鉴生物进化规律的一种随机全局性的搜索算法，用优胜劣汰、适者生存来解决寻优问题[18]。该方法具有很强的通用性、可操作性、并行性和鲁棒性。不过，遗传算法容易陷入局部最优，因此需要通过设计得当的初始化种群有效避免陷入局部最优。

利用遗传算法优化支持向量机的惩罚参数c和核函数参数g，具体步骤如下：

(1)初始化参数，设置最大迭代次数和种群数量分别为100和20，交叉概率为0.9，惩罚参数c和核函数参数g的范围都为0～100，交叉验证次数为5。

(2)初始化种群得到初始适应度。

(3)利用该初始种群对训练集进行训练，得到SVM模型，由该模型对测试集进行测试。

(4)根据适应度对种群进行选择、交叉、变异，选择出下一代种群，即为参数。

(5)由得到的参数对SVM模型进行训练和测试，计算适应度；如果得到最佳适应度或者达到迭代次数，则停止，如果不满足，则返回第(4)步。

3 实验结果与分析

3.1 实验条件和振动信号

借助千鹏旋转机械故障诊断平台来验证上述方法的有效性。该试验台由变速驱动电机、轴承、齿轮箱、轴、偏重转盘(2只)、调速器等组成，如图2所示。

图2 故障诊断平台示意图

其配置部件如表1所示。

表1 故障诊断平台部件表

实验中，采用加速度传感器对齿轮箱箱体的垂直径向、水平径向与轴向方向布点并采集振动信号。采样频率为5 120 Hz，变速箱转速为1 500 r/min，其载重电流0.2 A。齿轮箱的4种故障状态为：正常、点蚀、磨损、断齿。这4种故障状态各采集52个故障样本，每个故障样本均包含1 024个采样点。

3.2 特征提取

采用db5小波对4种故障类型的齿轮箱振动信号进行三层小波包分解降噪，得到8个小波系数变化序列，如图3所示。其中，S3,0表示相似小波系数序列，S3,1～S3,7表示细节小波系数序列。

图3 齿轮箱不同故障状态下的小波系数序列

从图3可以看出，其点蚀、磨损、断齿故障状态下的细节小波系数序列S3,1～S4,1差异十分明显，齿轮的故障类型不同, 各个节点的最大小波包系数就会发生变化, 为提高特征灵敏度和稳定性，可对小波系数重构，从而获得第三层8个节点的小波包能量。即用4个时域统计特征参数(峭度、裕度、峰值、方差)和16个时频域特征参数(8个节点的最大小波包系数和小波包能量)来描述齿轮的运行状态，它们构成一组完整的20维特征样本。其部分特征样本如表2所示。

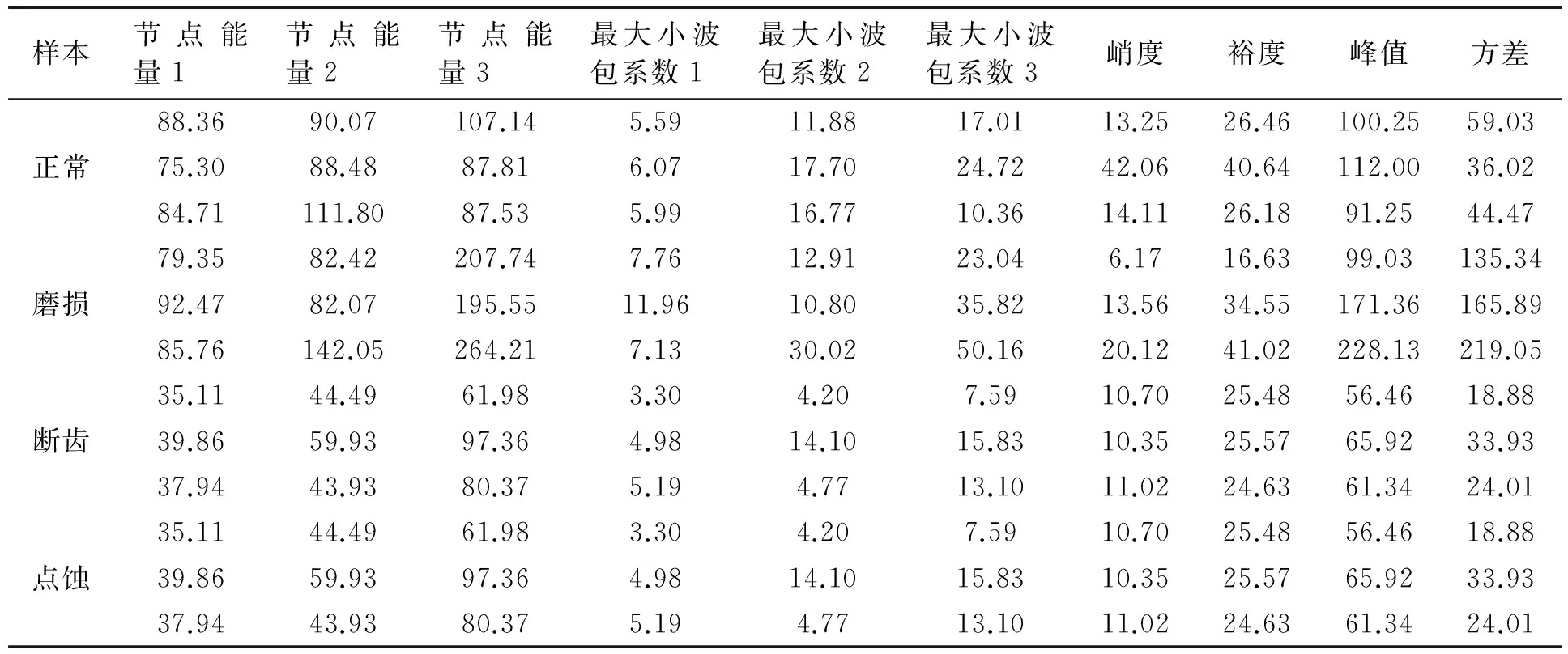
表2 多特征融合样本

3.3 故障诊断

齿轮的4种故障状态各采集52组样本，共208组样本，经过归一化处理，提取20维特征向量。每类选取前32组特征样本作为训练样本，输入到4个支持向量机组成的多故障分类器中进行训练(1正常，2磨损，3断齿，4点蚀)。剩余的20组特征样本作为测试样本，输入到训练好的GA优化SVM模型中进行故障诊断。设置种群规模为20，迭代次数为100，交叉概率为0.9，变异概率为0.1，交叉验证次数为5，c和g的范围为0～100，GA优化SVM适应度与分类如图4所示。

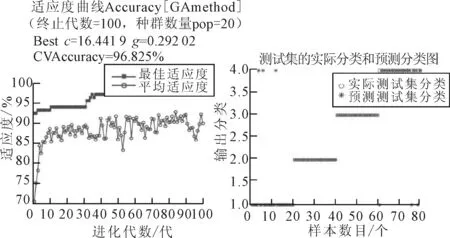
图4 GA优化SVM适应度与分类图

用最佳适应度表示交叉验证的最大精度，用平均适应度表示交叉验证的平均精度。由图4可知，在融合多特征作为特征向量情况下，其最佳适应度达到了96.825%，惩罚参数c和核函数参数g分别为16.442，以及0.292。该方法的分类准确率达到了92.5% (74/80)。另外，轻微故障点蚀的分类与正常分类各有3个数据错分。然而，实际工程应用中，磨损和断齿会影响到齿轮箱的输出轴进给动作和速度，轻微的点蚀则不会影响输出轴的正常运行，因而它对指导实际维修维护几乎没有影响。当然，如果需要研究齿轮早期故障情况，点蚀的正确分类自然极为重要。这需要对数据的特征向量进一步优化，从而保证更准确的分类。而如果不融合4个时域统计参数，仅仅用小波包分解获得的时频域特征(各个节点能量以及最大小波包系数)作为特征向量，则其准确率为88.75% (71/80)，其对应的优化参数如表3所示。

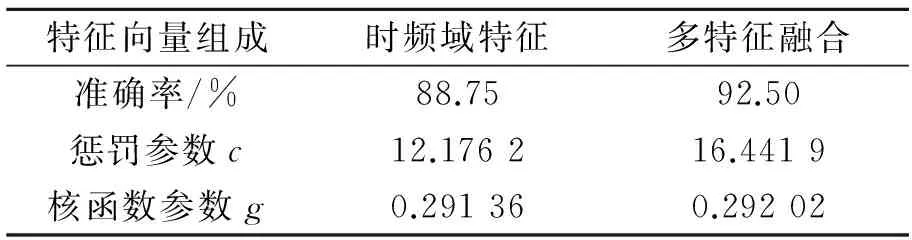
表3 融合多特征与未融合情况下各参数对比

从表3可以看出，在融合了多特征后，后续分类器的故障识别精度更高。为了对比更清晰，笔者将使用其他方法，如粒子群算法(Particle Swarm Optimization，PSO)优化SVM，网格搜索算法(Grid Search，GS)优化SVM。设置PSO的种群规模为20，迭代次数为100，c1、c2为2.05，k为0.6，交叉验证次数为5，c和g的范围为0～100。其结果如图5所示。

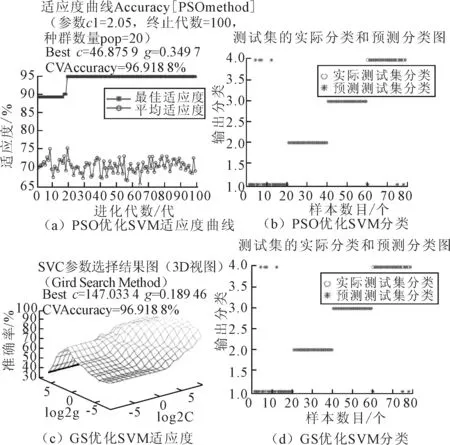
图5 PSO、GS优化SVM

由图5可以看出，PSO优化后的准确率(73/80)比GA优化后的准确率低，且其适应度较低，为94.918 8%，容易陷入局部最优，导致不能遍寻最优的惩罚参数和核函数。如果在扣除不佳的实验数据，采用更多、更有效的数据，那么在分类过程中，将会因为陷入局部最优导致不是最佳的c和g，会降低准确率。此外交叉验证作为对该算法的精度估计，精度越低，算法准确性越差。使用网格搜索寻优，不仅准确率偏低91.25%(73/80)，而且适应度更低，即精度低。PSO和GS优化SVM的惩罚参数c的值都偏大，分别为46.875 9、147.033 4，惩罚参数越大，越不能容忍出现误差，泛化能力差。很明显，GA优化SVM的效果更佳，其整体参数如表4所示。

表4 三种方法故障诊断对比

4 结论

笔者对齿轮箱的原始振动信号进行三层小波包分解，从而获取各个节点的最大小波包系数和小波包能量，融合4个时域统计特征参数，构成特征样本，将其输入遗传算法优化的支持向量机中，对齿轮的故障状态进行诊断得出：相对于时频域特征，多特征融合能更好地表征齿轮的运行状态，并有利于提高遗传算法优化支持向量机的故障分类精度；相比PSO优化SVM以及网格搜索寻优SVM算法，GA优化SVM能获得更优的惩罚参数c和核函数参数g，具有更高的故障识别能力。

[1] 刘天宇,李国正.齿轮故障不均衡分类问题的研究[J].计算机工程与应用,2010，46(20):146-148.

[2] Omar F K,Gaouda A M.Dynamic Wavelet-based Tool for Gearbox Diagnosis[J].Mechanical Systems and Signal Processing, 2012，26:190-204.

[3] Lei Y G. Machinery Fault Diagnosis Based on Improved Hilbert-Huang Transform[J]. Journal of Mechanical Engineering, 2011，47(5):71-77.

[4] Bin G F, Gao J J. Early Fault Diagnosis of Rotating Machinery Based on Wavelet Packets—empirical Mode Decomposition Feature Extraction and Neural network[J]. Mechanical Systems and Signal Processing,2012，27:696-711.

[5] 刘石,屈梁生.回转机械故障诊断中的三维全息谱技术[J].西安交通大学学报, 2004，38(9):900-903.

[6] 罗荣,田福庆,冯昌林,等.冗余小波包改进及其在齿轮箱故障诊断中应用[J].机械工程学报,2014，50(15):82-88.

[7] Peng Z K,Jackson M R,Rongong J A,et al.On the Energy Leakage of Discrete Wavelet Transform[J]. Mechanical Systrms and Signal Processing,2009，23:331-342.

[8] 袁静.机械故障诊断的内积变换原理与多小波特征提取方法研究[D].西安：西安交通大学，2011.

[9] WANG Y X,HE Z J,ZI Y Y. Enhancement of Signal Denoising and Multiple Fault Signatures Detecting in Rotating Machinery Using Dual-tree Complex Wavelet Transform[J]. Mechanical Systems and Signal Processing,2010，24:120-136.

[10] WANG D,SHEN C Q,TSE P W. A Novel Adaptive Wavelet Stripping Algorithm for Extracting the Transients Caused by Bearing Localized Faults[J]. Journal of Sound and Vibration,2013，332： 6871-6889.

[11] 申中杰，陈雪峰.基于相对特征和多变量支持向量机的滚动轴承剩余寿命预测[J].机械工程学报,2013，49(2):183-189.

[12] 钱士才,孙宇昕.基于支持向量机的震颤在线智能检测[J].机械工程学报,2015，51(1):1-8.

[13] 郭远晶.面向风电齿轮箱的角域振动信号处理与故障诊断方法研究[D].杭州：浙江大学，2015.

[14] 秦波,刘永亮.EMD分解与多特征融合的齿轮故障诊断方法[J].机床与液压，2016，44(3):188-192.

[15] 秦波,刘永亮,王建国,等.基于小波包最优节点能量特征的BA-ELM齿轮故障诊断方法[J].机械传动,2016(4):33-37.

[16] Vapnik V. The Nature of Statistical Learning Theory[M]. New York:Springer Verlag, 1995.

[17] 李大中.基于EMD与GA-SVM的超声检测缺陷信号识别[J].中国测试,2016,42(1):102-106.

[18] Fei S, Zhang X. Fault Diagnosis of Power Transformer Based on Support Vector Machine with Genetic Algorithm[J].Expert Systems with Applications, 2009,36(8):11352-11357.