基于TACKF的海面目标航向航速估计算法
程然, 何科峰, 缪礼锋
(中国航空工业集团公司雷华电子技术研究所, 江苏无锡 214063)
0 引言
航向航速是海面目标的重要特征,能准确估计出航向航速对于海面目标的跟踪、识别和打击具有非常重要的意义。由于海面目标跟踪中易出现量测高精度、系统复杂强非线性等情况,导致传统非线性滤波器对海面目标航向航速的估计精度不高[1]。此外,海面运动目标自身速度较慢,滤波器的稳态波动对海面目标的航速估计影响较大,精度难以保证。针对以上问题,为了改善复杂环境下目标跟踪的性能,对海面目标航向航速精确估计算法的研究迫在眉睫。
近年来,国内对海面目标航向航速估计算法开展了广泛的研究。文献[2]针对海面目标航向航速估计的物理概念、真值的获取及考核方法作了初步的研究和介绍,但并没有考虑复杂情况下提高海面目标航向航速估计精度的具体途径。文献[3]推导出了雷达载体在高速运动条件下海面目标跟踪的滤波方程,并利用雷达载体的GPS信息和目标的测量信息实现了对目标航向航速的高精度解算。然而这种方法仅在海面目标作匀速直线运动时估计精度才较高,当目标发生机动(如协同转弯)时,所建目标的运动学模型与目标的实际运动模式不匹配,导致滤波器发散,最终造成目标的跟踪丢失。鉴于以上问题和不足,本文紧密结合工程应用背景,针对海面目标跟踪中易出现的量测高精度、系统复杂强非线性等问题,提出了一种基于截断的自适应容积卡尔曼滤波算法(TACKF)的海面目标航向航速估计算法。
首先,本文简要介绍了非线性高斯滤波器(GF)的基本原理,分析了GF在量测更新阶段所存在的主要问题。其次,本文简要阐述了截断卡尔曼滤波器(TKF)的基本原理,并引入了一种自适应调节机制,将TKF与容积卡尔曼滤波器(CKF)通过一个自适应变化的参数有机地结合起来,从而推导得出截断的自适应容积卡尔曼滤波器(TACKF)。最后,结合数值仿真及实验数据将本文所提出的滤波算法应用到海面目标的航向航速估计中,数据仿真结果证明了该算法的有效性。
1 GF算法结构
考虑如下形式的状态空间离散非线性系统:
(1)
式中,xk∈Rnx表示k时刻系统状态向量(nx为状态维数),zk∈Rnz表示k时刻外部量测向量(nz为状态维数),f(·)表示状态转移函数,h(·)表示量测函数,wk-1与vk分别表示系统噪声和量测噪声,二者互不相关且均为零均值高斯白噪声,即wk-1~N(0,Qk-1),vk~N(0,Rk)。依据线性最小方差准则,GF的一般结构[4]为
(2)
式中,
(3)
式中,Zk-1表示直到k-1时刻所有的量测信息。从上述GF的一般结构可知,GF可分为两个部分,即时间更新和量测更新。GF的估计精度主要取决于对系统状态均值和协方差的计算精度。传统GF对式(3)通常采用近似的方法获得,例如无迹卡尔曼滤波器(UKF)采用Unscented变换的近似方法[5];容积卡尔曼滤波器(CKF)采用容积变换的近似方法[6],不同的近似方法会得到不同的估计精度。
2 TKF算法概要
2.1 GF量测更新阶段分析
(4)
(5)
GF中,状态与量测近似的条件联合概率密度函数[7]为
(6)
(7)
(8)
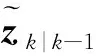
为了表示近似的条件联合概率密度函数与真实的条件联合概率密度函数的偏差程度,文献[7]给出了一种计算KLD偏差参数的表示方法,并以此来表征GF的估计精度。KLD参数值越小,表明GF对状态真实后验概率密度函数的逼近程度越高。KLD参数本质上是一个近似化的指标参数,它是建立在对非线性量测函数一阶线性化基础之上的,具体表达式[7]为
(9)

(10)

(11)
(12)
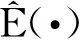
对EKF来说,由于它只对量测函数进行一阶泰勒展开并忽略所有高阶矩信息,因此EKF的KLD参数表达式[7]整理为
(13)
(14)
从EKF的KLD表达式中可以看出,EKF的估计精度主要取决于3个因素,即量测噪声方差、系统状态的先验协方差及量测函数。对于确定的系统状态先验分布及量测函数,当量测噪声方差减小时,EKF的KLD参数升高,此时EKF对系统状态真实的后验概率密度函数逼近精度变差。而当量测噪声方差和量测函数一定,随着系统状态的先验不确定性逐渐加强,即系统状态的先验协方差逐渐增大,同样会使KLD参数升高,系统状态的估计精度下降。
对于UKF,CKF等利用确定性采样策略的传统GF而言,由于考虑了系统状态的高阶矩信息,因此在精度上要优于EKF。它们的KLD表达式本质上是一样的,唯一区别就是采样点的选取方式不同。因此,这类GF对系统状态真实后验概率密度函数的近似精度同样受到量测噪声方差、状态先验协方差及非线性量测函数的影响,分析过程同EKF相似,不再赘述。
2.2 TKF原理分析
通过前面的分析可以得出这样一个结论,即在量测高精度、系统复杂强非线性的情况下传统GF对系统状态后验概率密度函数的近似精度不是很高。为了解决这一问题,文献[8]提出了一种截断的卡尔曼滤波器(TKF)。TKF的滤波结构框架与传统GF大体相同,唯一的区别在于TKF在时间更新阶段对系统状态的先验分布进行了截断处理,因此本节只分析TKF在时间更新阶段的滤波原理。
与之前的分析有所不同,假设此时的量测是高精度的,也就是说量测噪声的方差足够小,那么我们认为以下的近似是合理的,即将服从高斯分布的量测噪声近似为服从均匀分布,且近似后的量测噪声均值和方差保持不变[8]。因为量测噪声方差足够小,这就意味着近似为均匀分布后的量测噪声被限制在一个很小的区域内,因此我们认为此时系统状态的先验概率密度函数在其相应的定义域内可以近似为一个常数[8]。

(15)
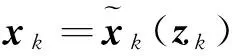
(16)
整理,得
(17)
似然概率密度函数表示为
p(zk|xk)=pvk(zk-h(xk))Ix(xk)
(18)
(19)
式中,Ix表示截断的区域:
(20)
根据贝叶斯准则,系统状态的后验概率密度函数可表示为
p(xk|Zk)∝p(zk|xk)p0(xk|Zk-1)=
pvk(zk-h(xk))Ix(xk)p0(xk|Zk-1) (21)
式(21)可以看作是系统状态的先验概率密度函数被“截断”了,故截断的系统状态先验概率密度函数可表示为

(22)
式中,p1(·)表示截断的系统状态先验概率密度函数,ε表示归一化常数,表示为
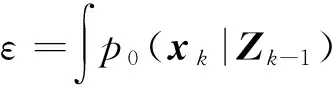
(23)
将式(17)代入式(23),得
(24)
整理,得
式中,|Iv|表示近似成均匀分布的量测噪声统计分布区域的面积。则截断的先验均值为
(26)
将式(17)代入式(26)整理,得
因为量测噪声的均值没变,即
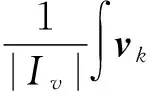
(28)
将式(28)代入式(27)整理,得
(29)
截断的系统状态先验协方差为
(30)
将式(17)代入式(30),得
(31)
整理,得
(32)
从式(32)可以看出,在TKF的时间更新阶段,系统状态的先验协方差与量测噪声的方差建立起了联系。根据前面介绍的KLD参数理论,当系统状态的先验协方差随量测噪声方差作相同趋势的变化时,会抵消KLD参数的整体变化,从而使得滤波器对系统状态真实的后验概率密度函数的逼近程度不会受到外部高精度量测的显著影响。同时,文献[7]还指出,当系统状态的先验协方差减小时会减轻外部量测非线性对GF量测更新阶段的影响。对系统状态的先验概率密度函数进行截断处理,相当于增加对系统状态先验估计的置信程度,降低了系统状态的先验不确定性,从而使整个滤波器的估计性能得到进一步提升。
3 TACKF算法推导
本节将引入一种自适应调整机制,将TKF与某种GF通过一个自适应变化的参数相结合,使其能够根据外部量测信息的变化动态地调整二者相对权值的大小,从整体上提高滤波性能。由于CKF具有算法实现简单、滤波精度高、收敛性好等优点,且具有更高的数值稳定性[6],因此本节拟采用TKF与CKF有机相结合的方法得到TACKF算法。
3.1 TKF与CKF自适应调整机制
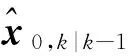
(33)
式中,α∈[0,1]是一个自适应变化的参数。
从前面对GF量测更新阶段的分析中可知:当外部量测噪声方差和量测函数一定时,随着系统状态先验协方差的逐渐增大(系统状态的先验不确定性逐渐增强),GF的KLD参数会逐渐升高,从而导致系统状态的估计精度下降。同时文献[8]指出,当外部量测信息较为丰富时,TKF相比于传统GF能够发挥更好的滤波性能。而当外部量测信息相对匮乏时,TKF的优势则被削弱,传统GF的滤波性能得到改善。
基于这两个结论可以看出:当外部量测信息较为丰富时,TKF系统状态的先验不确定性比CKF的弱,TKF相比于CKF能够发挥更好的滤波性能;相反,当外部量测信息相对匮乏时,TKF中系统状态的先验不确定性比CKF的强,TKF的优势被削弱,CKF的滤波性能得到改善。故可以将自适应变化参数α的选取与系统状态的先验协方差建立起一种关系,从而更加明确α的取值:
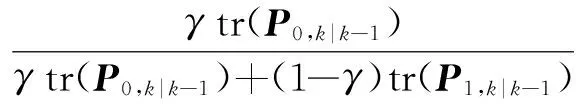
(34)
式中,γ是一个用户设定的预调整参数,它可以预先调整系统状态先验协方差矩阵迹的相对权重大小来改善参数α的自适应调整。从式(34)可以看到,当γ取值减小时,说明截断的系统状态先验概率密度函数的相对权重被逐渐削弱;反之当γ取值增大时,则说明要对截断的系统状态先验概率密度函数的相对权重逐渐加强。
当γ取值一定时,随着外部量测信息逐渐变得丰富,TKF系统状态的先验不确定性逐渐降低,自适应变化参数α逐渐趋于1,此时TKF发挥主要作用,当α=1时滤波器则转化为纯粹的TKF;相反,随着外部量测信息逐渐变得匮乏,TKF系统状态的先验不确定性逐渐升高,自适应变化参数α逐渐趋于0,此时CKF发挥主要作用,当α=0时滤波器则完全退化为CKF。故TKF与CKF的这种自适应调整机制能够更好地适应外部量测信息的变化,从整体上提高滤波器的滤波性能。
3.2 TACKF滤波算法
与传统GF的滤波结构相同,TACKF也是由时间更新和量测更新两部分组成,具体实施步骤如下。
1) 时间更新
通过Cholesky分解状态的协方差矩阵Pk-1|k-1:
(35)
根据Spherical-Radial Cubature准则计算容积点:
(36)
(37)
通过状态方程传播容积点:
(38)
计算CKF中系统状态的先验均值及协方差矩阵:
(39)
计算TKF中系统状态的先验均值及协方差矩阵:
(40)
2) 量测更新
通过Cholesky分解Ph,k|k-1(h∈{0,1}):
(41)
根据Spherical-Radial Cubature准则计算容积点:
(42)
通过量测方程传播容积点:
Zh,i,k|k-1=h(Xh,i,k|k-1)
(43)
计算量测的先验均值及自相关先验协方差矩阵:
(44)
计算互相关协方差矩阵:
(45)
分别计算CKF和TKF的卡尔曼滤波增益:
(46)
分别计算CKF和TKF状态的后验均值及协方差:
(47)
计算系统状态最终的后验均值及协方差矩阵:
(48)
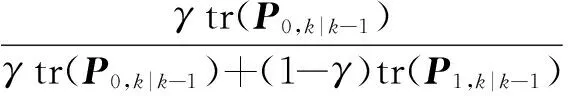
(49)
4 仿真与分析
4.1 数值仿真验证
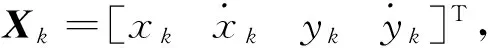
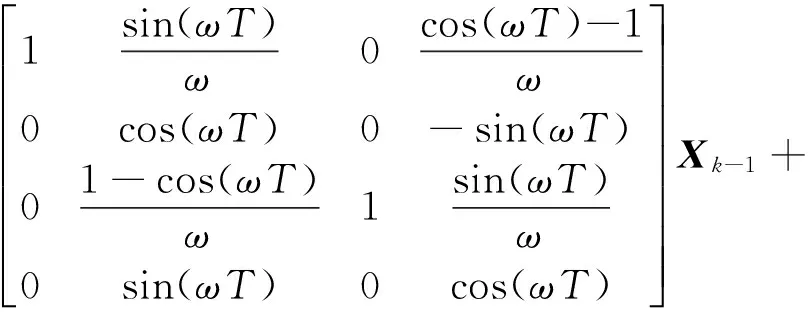
(50)
式中,ω表示海面目标转弯角速率,T表示机载雷达采样周期,wk-1表示高斯系统噪声。系统噪声方差矩阵Qk-1为
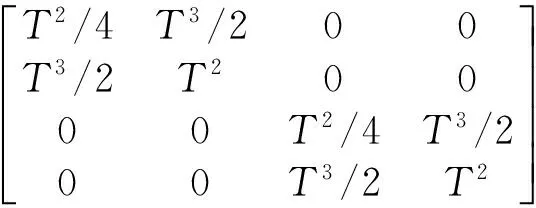
(51)
量测方程表示为

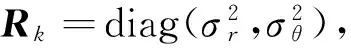
从数值仿真结果中可以看出,当海面目标作协同转弯运动时,TACKF对目标航向航速的估计精度要明显高于CKF及UKF。而当海面目标作匀速直线运动时,3个滤波器对目标航向航速的估计精度相当。证明了在量测高精度、系统复杂强非线性的条件下TACKF能够更有效地逼近系统状态的后验概率密度函数,从而有效提高了海面目标航向航速的估计精度。
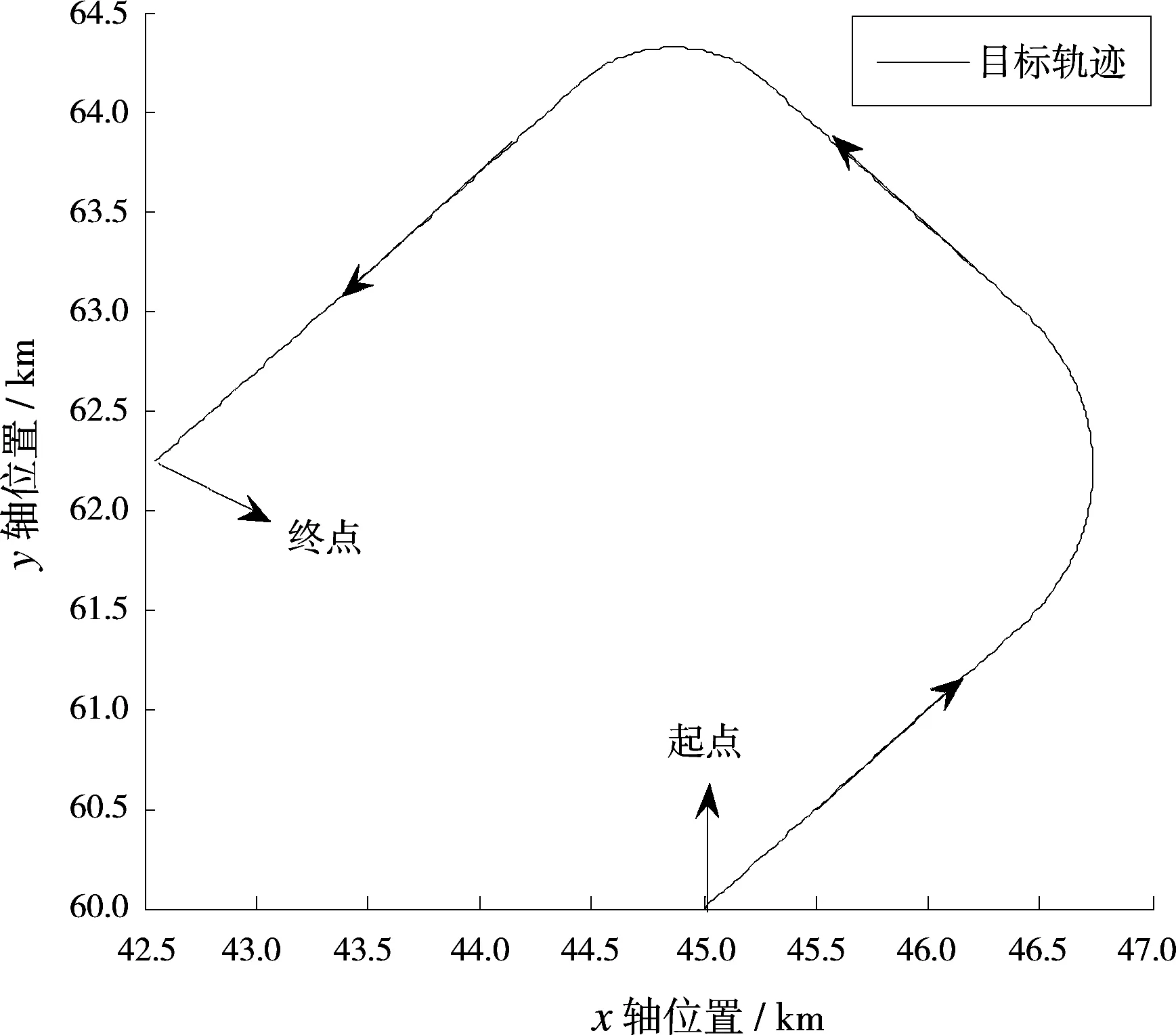
图1 海面目标运动轨迹
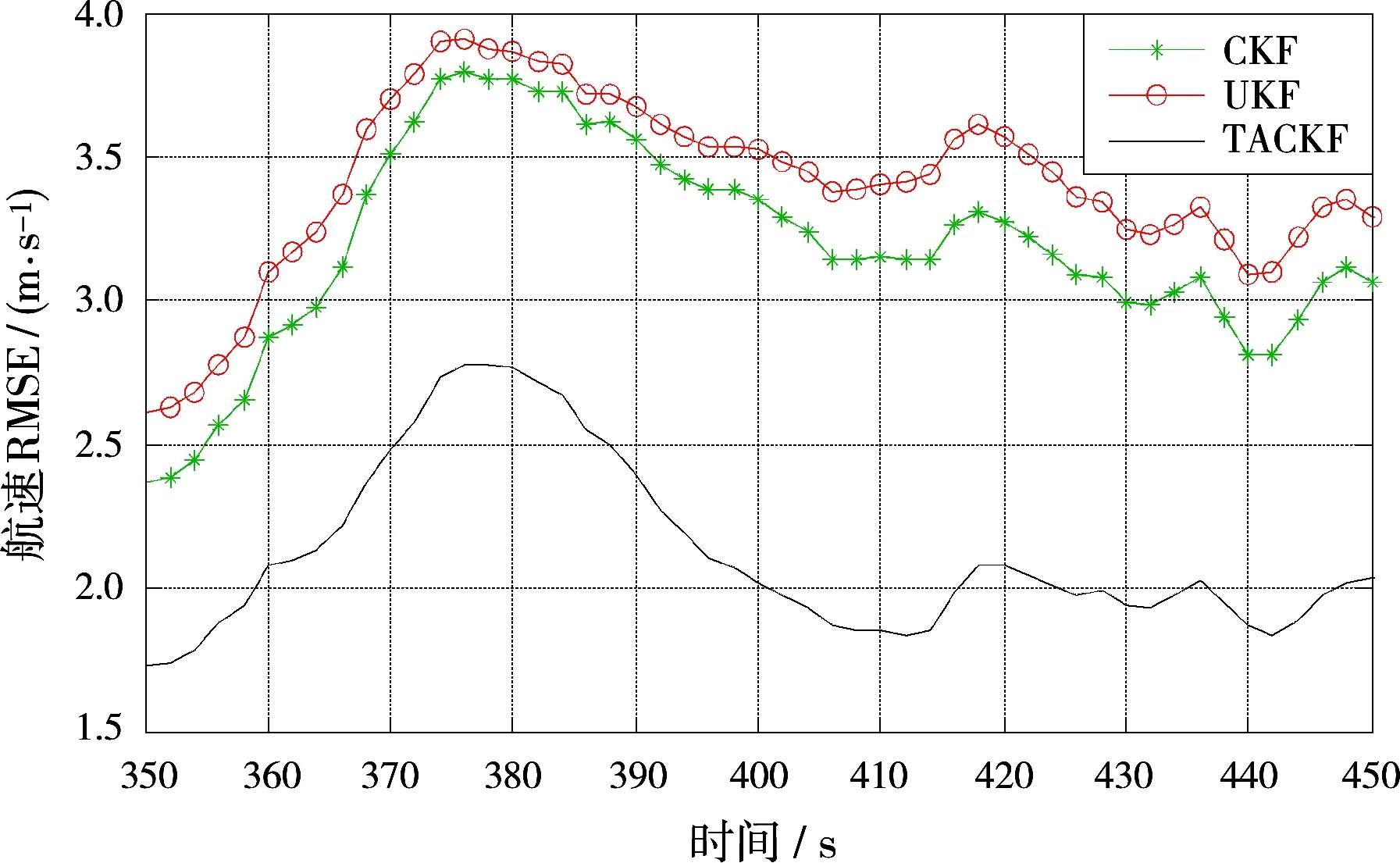
图2 各滤波器对海面目标航速估计的RMSE曲线
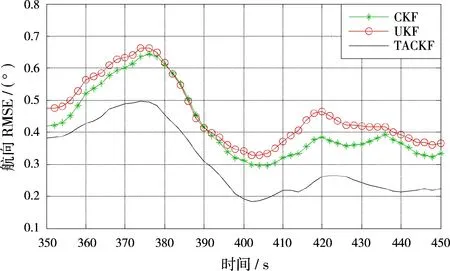
图3 各滤波器对海面目标航向估计的RMSE曲线
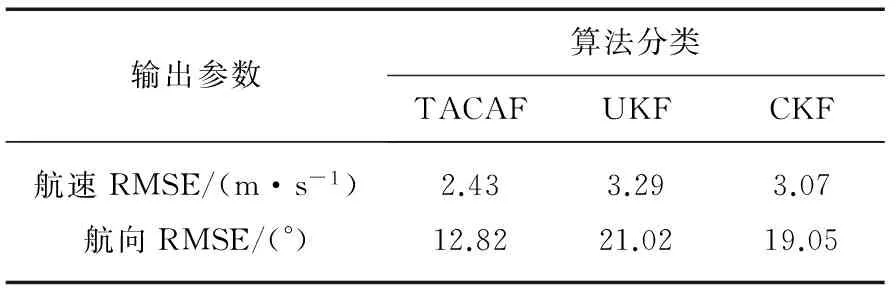
输出参数算法分类TACAFUKFCKF航速RMSE/(m·s-1)航向RMSE/(°)2.4312.823.2921.023.0719.05
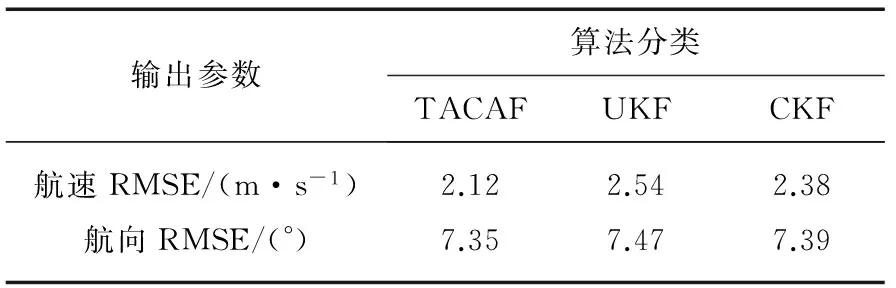
表2 匀速运动段目标航向航速估计精度统计
4.1 实验数据验证
结合实验数据将本文所提出的滤波算法应用到对海面目标航向航速的离线估计中,分别给出在不同时间统计区间内各滤波器的图像对比分析和数据精度分析,结果如表3、图4、图5所示。
结合实验数据的仿真结果可以看出,相比于EKF,本文所提出的TACKF算法能够发挥更好的滤波性能,具有更高的滤波精度,更适于应用到海面运动目标的航向航速估计中。
5 结束语
本文紧密结合工程应用背景,针对海面目标跟踪中易出现的量测高精度、系统复杂强非线性等问题,提出了一种基于截断的自适应容积卡尔曼滤波算法(TACKF)的海面目标航向航速估计算法。通过引入一种自适应调整机制,将TKF与CKF有机地结合起来,使其能够根据外部量测信息的变化动态地调整二者相对权值的大小,有效改善了滤波器的估计性能。结合实验数据将本论文所提出的滤波算法应用到对海面目标航向航速的离线估计中,分别给出在不同时间统计区间和内各滤波器的图像对比分析数据精度分析。仿真结果表明,本论文所提出的滤波算法较传统的非线性滤波算法有显著的性能提升,可以有效提高复杂环境下海面目标航向航速的估计精度。

表3 海面目标航向航速估计数据精度统计
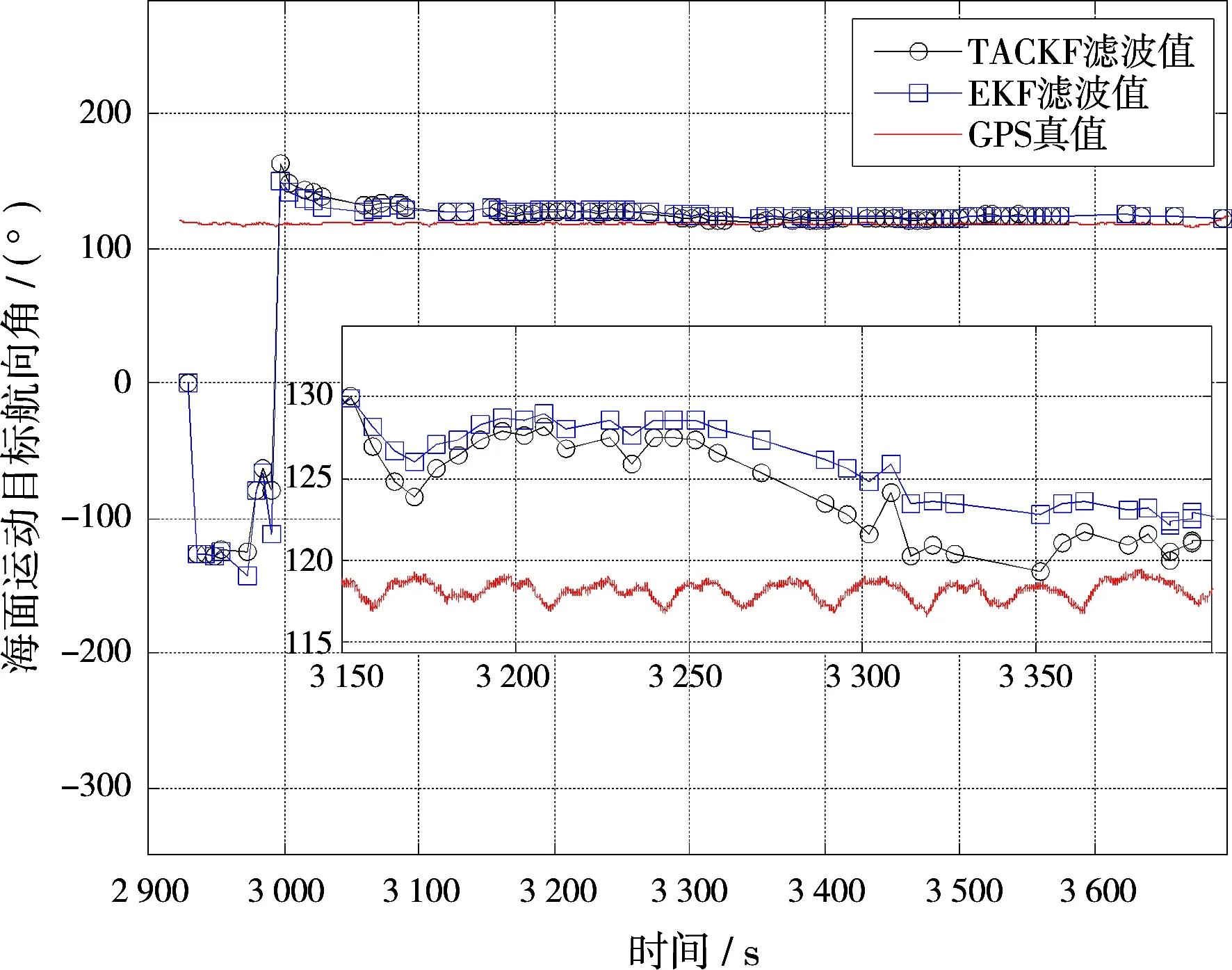
图4 各滤波器对海面目标航向角的估计结果
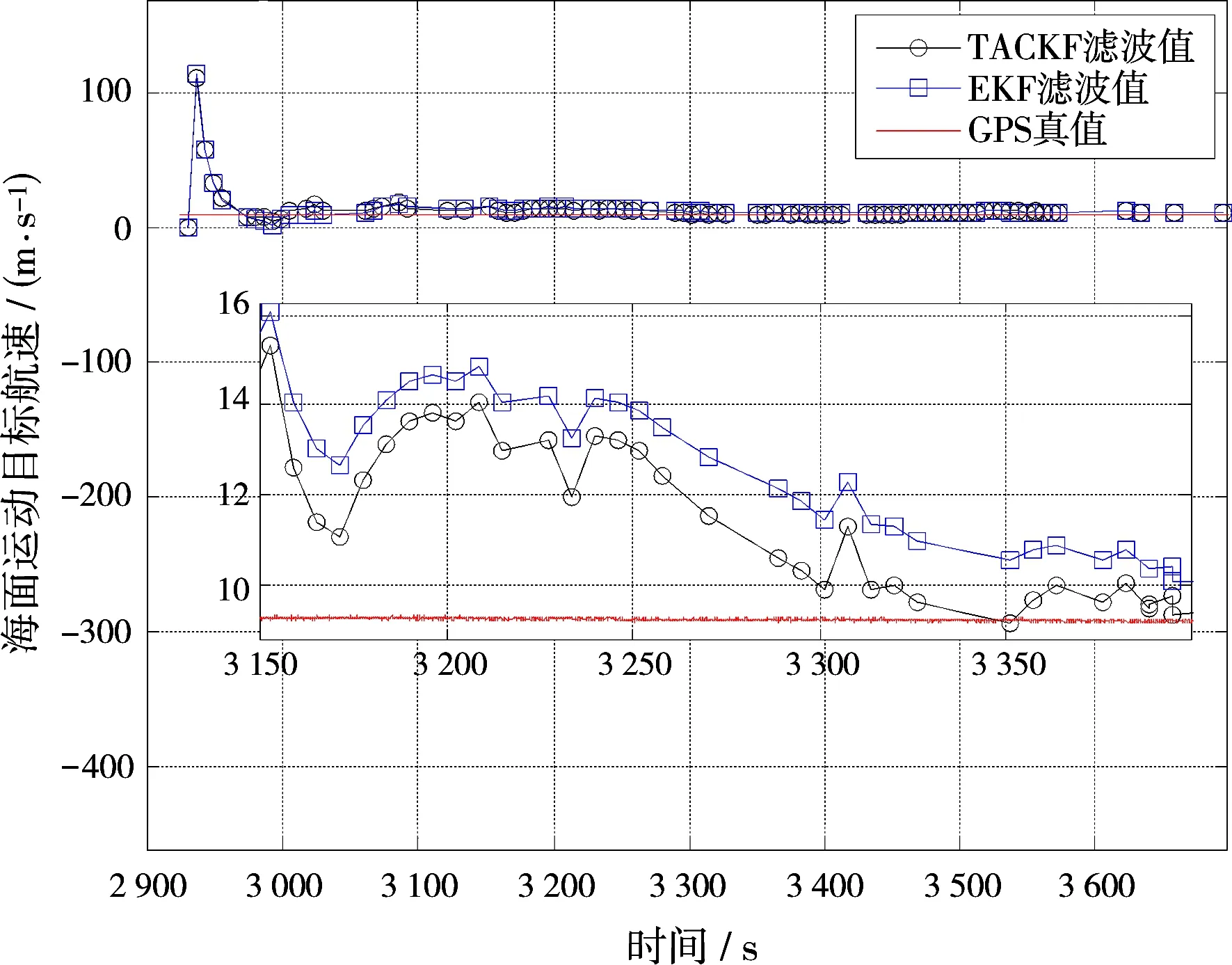
图5 各滤波器对海面目标航速的估计结果
[1]徐晋,付启众,陆鹏程,等. 米波雷达对海面目标探测性能分析及验证[J]. 雷达科学与技术, 2012, 10(4):376-379. XU Jin, FU Qizhong, LU Pengcheng, et al. Analysis and Experiment Verification of Maritime Target Detection Performance of Meter-Wave Radar[J]. Radar Science and Technology, 2012, 10(4):376-379.(in Chinese)
[2]袁桂生. 目标航向航速解算及验证方法研究[J]. 雷达与对抗, 2009(1):26-29.
[3]黄孟俊,陈建军,赵宏钟. 海上目标航向航速解算新方法[J]. 信号处理, 2011, 27(7):1034-1038.
[4]张勇刚,黄玉龙,武哲民,等. 一种高阶无迹卡尔曼滤波方法[J]. 自动化学报, 2014, 40(5):838-848. ZHANG Yonggang, HUANG Yulong, WU Zhemin, et al. A High Order Unscented Kalman Filtering Method[J]. Acta Automatica Sinica, 2014, 40(5):838-848.(in Chinese)
[5]CHANG Lubin, HU Baiqing, LI An, et al. Transformed Unscented Kalman Filter[J]. IEEE Trans on Automatic Control, 2013, 58(1):252-257.
[6]JIA Bin, XIN Ming, CHENG Yang. High-Degree Cubature Kalman Filter[J]. Automatica, 2013, 49(2):510-518.
[7]MORELANDE M R, GARCIA-FERNANDEZ A F. Analysis of Kalman Filter Approximations for Nonlinear Measurements[J]. IEEE Trans on Signal Processing, 2013, 61(22):5477-5484.
[8]GARCIA-FERNANDEZ A F, MORELANDE M R, GRAJAL J. Truncated Unscented Kalman Filtering[J]. IEEE Trans on Signal Processing, 2012, 60(7):3372-3386.

