O2分子B3态势能曲线的从头计算∗

李晨曦 郭迎春† 王兵兵

1)(华东师范大学物理与材料科学学院,上海 200241)

2)(中国科学院物理研究所,凝聚态物理国家重点实验室,光物理实验室,北京 100190)

O2分子B3态势能曲线的从头计算∗

李晨曦1)郭迎春1)†王兵兵2)

1)(华东师范大学物理与材料科学学院,上海 200241)

2)(中国科学院物理研究所,凝聚态物理国家重点实验室,光物理实验室,北京 100190)

(2017年1月27日收到;2017年3月15日收到修改稿)

B3态是O2的最强的三重跃迁(B3←X3)Schumann-Runge(SR)带的上态,SR吸收带在保护地球、阻止紫外辐射等方面起着关键作用.SR连续带的光解离是平流层O原子及O3的主要来源,掌握详细准确的O2分子的电子态势能曲线,有助于对这些光谱现象的深入理解.本文通过MOLPRO软件,采用包含Davison修正的内收缩的多参考组态相互作用(icMRCI+Q)方法,对O2的B3态的势能曲线进行了计算,采用的多参考组态函数来自完全活性空间自洽场计算.首先,采用共价组态构成多参考组态,对和态对称性相同的四个态进行了态平均计算,发现B3态不存在双势阱结构,文献(Spectrochimica Acta Part A:Molecular and Biomolecular Spectroscopy 2014 124 216)中双势阱的产生是根的振荡(rootfl ipping)造成的,即B3态的势能曲线在核间距约为0.2 nm处跳变到能量相近的23∆态的势能曲线上.本文中的态平均计算避免了这种根的振荡.接着,采用完全活性空间组态相互作用的方法计算B3态的势能曲线,通过改变活性空间的轨道组成,发现带有2πu轨道电子布居的里德伯组态对B3态的束缚态的特征的出现是必不可少的.最后,通过将2πu轨道加入到活性空间中,实现将相关的里德伯组态加入到多参考组态,对态的势能曲线进行了icMRCI+Q计算,得到相较于以往的理论计算与实验值更加相近的势能曲线以及光谱常数.本文探讨里德伯组态贡献的过程为如何确定多参考组态相互作用计算中的参考组态、提高理论计算的准确度提供了可以借鉴的途径.

∶O2分子的B3态,多参考组态相互作用,势能曲线,光谱常数

1 引 言

O2在大气中含量第二,在星际化学中发挥着重要作用.详细的O2电子态的知识,尤其是它的势能曲线,有助于我们理解复杂的O2光谱、氧原子间的碰撞过程以及涉及氧分子反应的化学反应机制.本文主要对O2的B3态的势能曲线进行了精确计算.

B3态是O2的最强三重跃迁(B3←X3)Schumann-Runge(SR)带的上态[1,2],SR吸收带在保护地球、防止紫外辐射起着关键作用.SR连续带的光解离是平流层氧原子及O3的主要来源[3−5].B3态很早就受到高度关注和广泛的研究.1972年,Krupenie[2]总结了实验上关于O2的数据,给出了B3态的平衡核间距、解离能以及振转常数.1986年,Lewis等[6]进一步提高B3态的光谱数据的精度,给出了更为精确的振转常数以及Rudberg-Klein-Rees(RKR)势能曲线.理论上,1977年,Saxon和Liu[7]采用组态相互作用的方法研究了O2的62个共价分子态,给出了完整的B3态的势能曲线数据.但是,Buencker等[8]发现,B3态还具有一定的里德伯态特征.1979年,Tatewaki等[9]根据波函数中里德伯组态的权重,明确指出在核间距小于0.12 nm时,态是里德伯态,在核间距大于此值时,它是共价态.2001年,Muller等[10]采用多参考组态相互作用的方法研究了O2的B3态等电子态在势能计算中的基组扩大效应,发现电子态B3态的基组扩大并没有带来规律性的明显改善,提出参考组态空间加入里德伯轨道后B3态的结果将有所改善,但他们并没有给出具体的结果.2014年,Liu等[11]采用内收缩的多参考组态相互作用的方法,研究了22个O2的分子态势能,提出B3态具有双势阱,给出了双势阱的平衡位置、解离能以及振动常数.但是实验上并没有观察到与势能双阱结构相对应的结果.

本文采用包含Davidson修正[12]的内收缩多参考组态相互作用(internally contracted multireference configuration interaction including Davison correction,icMRCI+Q)的方法[13,14]对态的势能曲线进行研究.本文安排如下∶第2部分简要介绍采用的方法以及光谱常数如何获得;第3部分首先证明了B3态双势阱结构不存在,指出了文献中计算出双势阱的可能原因;接着,采用完全活性空间组态相互作用(complete active space self-consistent field,CASSCF)方法探讨了2πu轨道构成的里德伯组态对B3的势能曲线的影响;最后,采用参考组态中包含了里德伯组态的icMRCI+Q方法,计算出B3态的势能曲线以及光谱常数,与实验结果和以前的计算进行了比较;第4部分给出结论.

2 理论方法

2.1 势能曲线的计算

本文采用的icMRCI+Q方法有如下步骤∶首先采用Hartree-Fock(HF)自洽场方法得到分子轨道,然后选取分子轨道构成活性空间进行CASSCF计算,得到的波函数作为多参考组态的波函数进行icMRCI+Q计算.计算是通过量化计算软件MOLPRO[13,14]实现的.

我们计算的是O2分子的解离到氧原子3P+1D态的最低激发态B3态的势能曲线,为避免根的振荡(rootfl ipping),上述的第二步和第三步我们都采用了对多个与B3态对称性相同且能量相近的态进行态平均计算[15].计算中采用的是D2h对称群,在此群下,和∆u对称性是相同的,所以态平均计算中涉及的态包含和23四个态,其中A′3∆u的解离极限是氧原子的态的解离极限是氧原子的3P+1D.

2.2 分子常数的计算

对于2.1节得到的离散的B3态的单点能数据,用核间距R的多项式进行拟合,从而得到精确的平衡核间距Re以及解离能De(势能曲线渐近线的值与平衡核间距的分子能量值的差值).

得到分子的势能曲线后,便可以代入核的薛定谔方程(见方程(1)),计算振转能级Eν,J,这一过程通过Level程序[16]实现.

由得到的振转能级向υ+1/2的多项式拟合,得到振动常数ωe,ωexe,ωeye,即

将Bυ向υ+1/2拟合,得到转动常数Be和αe,即

3 结果与讨论

3.1 B3态是否存在双势阱结构

首先采用与文献[11]一致的方法icMRCI+Q来考察B3态是否存在双势阱结构.和文献[11]一样,第二步的活性空间选取的轨道是原子的价电子轨道线性组合构成的分子轨道,包括2σg,2σu,3σg,3σu,1πu,1πg, 从而第三步所采用的参考组态波函数没有里德伯组态的贡献.采用的基组是aug-cc-pV5Z[17],在icMRCI+Q计算中对A′3∆u,B3,23∆u,23态进行态平均计算, 以避免根的振荡.图1(a)给出了这四个态的势能曲线,两个解离极限的差值为0.07196 Hartree,对应15793 cm−1,与1D氧原子和3P氧原子的能级差15867 cm−1相一致. 由图1(a)可见,B3Σ态没有双势阱结构,这与文献[11]中的B3态有两个势阱的结果相矛盾.所以我们在表1中给出了和23∆u态的平衡核间距Re,解离能De以及振动常数ωe,还列出了文献[11]中B3态的两个势阱的相应结果.由表1可见,本文计算的B3的结果和文献[11]中的第一个势阱的结果基本一致,二者的最大差值发生在第二位有效数字上,如的ωe值,本文的结果为710.31 cm−1,文献[11]的结果为723.60 cm−1.产生此差异的原因是文献[11]中采用了基组外推技术[18],考虑了1 s电子相关联[19]和相对论效应[20],这些效应修正了结果的第二、三位有效数字.由表1中还可见,本文计算的23∆u态的Re,De,ωe的结果和文献[11]中的第二个势阱的结果基本一致,从而怀疑文献[11]的双势阱结构是B3态在R=0.2 nm附近时发生了根的振荡,跳变至23∆u态势能曲线上.于是,我们采用icMRCI+Q,仅仅计算两个态A′3∆u和B3,而不是对接近解离极限区域能级较接近的四个态取平均,得到的B3的势能曲线与文献[11]的结果相一致,有两个势阱,如图1(b)中的粗黑实线所示.图1(b)中的淡实线分别对应图1(a)中的B3和23∆u态,图1(b)清楚地证实了上面的猜测.至此,说明了文献[11]中的B3态有双势阱结构的说法是错误的.

表1 B3态和23∆u态的分子常数Table 1. molecular constants for B3 and 23∆u states.

表1 B3态和23∆u态的分子常数Table 1. molecular constants for B3 and 23∆u states.

B3Σ−u (态平均计算) 0.16086 0.8824 710.31文献[11]中B3Σ−u的第一个势阱 0.15978 0.8417 723.60 1态平均计算) 0.232570.0660 186.98文献[11]中B3Σ−u的第二个势阱 0.232400.0632 186.88 23∆ u(

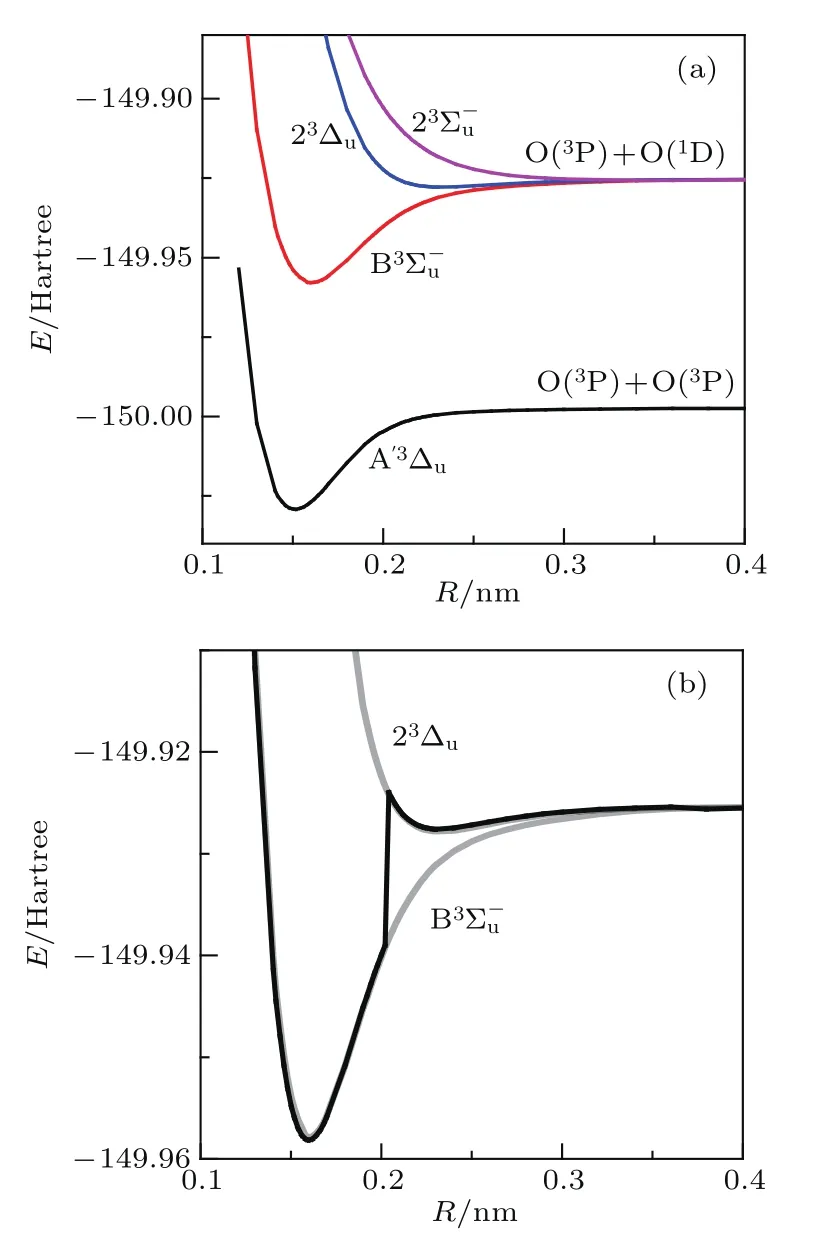
图1 采用icMRCI+Q/aug-cc-pV5Z方法得到的O2的A′3∆u,B3,23∆u 和23 态的势能曲线 (a) 对四个态进行态平均后得到的结果;(b)仅同时计算A′3∆u和B3态时得到的B3态的势能曲线(粗黑实线)Fig.1.The potential energy curves(PES)of A′3∆u,B3,23∆u and 23states of O2from icMRCI+Q/aug-cc-pV5Z:(a)The results from the 4 states average calculation;(b)the PES of B3(the thick dark solid line)when only calculating A′3∆uand B3.

3.2 B3态势能曲线的完全活性空间的计算

3.1 节中计算的B3态的平衡核间距Re和振动常数ωe与实验值(见表3)符合得很好,误差分别为0.00046 nm,1.21 cm−1.De误差很大,为0.12 eV.所以我们认为在3.1节的icMRCI+Q计算中缺少重要的参考组态.3.1节的计算中,参考组态仅包含共价组态,文献[8—10]都提到了波函数中里德堡组态的潜在的关键作用.文献[21,22]在采用MRCI方法成功计算与O2等价的体系S2的B3等态时,参考组态中包含了全价活性空间之外的3πu轨道构成的组态.所以我们将更高的非占据的2πu等轨道加入到完全活性空间中来构造出里德伯组态,采用CASSCF的方法来探讨里德伯组态对B3态的势能曲线的影响.本小节计算采用的基组都是aug-cc-pVTZ基组.计算中,为避免根的振荡,在平衡位置以后都采用了四个态的态平均计算.

图2给出了三种不同的活性空间下计算出的B3态的势能曲线.图2(a)情况下,活性空间仅由价电子轨道构成,即由2σg,2σu,3σg,3σu,1πu,1πg轨道构成.从而所考虑的组态由12个电子布居到这些轨道中所组成.其中σ轨道最高可布居2个电子,π轨道是二重简并轨道,最多可布居4个电子.计算结果表明,B3态的主要组态是2,以后用1,1来表示,如图2中的曲线(a)所示,该态的势能曲线是排斥态,没有束缚势阱.这显然是不正确的.所以这种情况下,活性空间中显然缺少决定B3态是束缚态的关键组态.

图2 不同活性空间下由CASSCF/aug-cc-pVTZ方法得到的B3态的势能曲线Fig.2.Potential energy curves for B3state by CASSCF/aug-cc-pVTZ with different complete active spaces.

图2(b)是将2πu加入到活性空间,从而活性空间包含轨道2σg,2σu,3σg,3σu,1πu,1πg,2πu,得到的B3态的势能曲线(图2中的曲线(b))有了束缚态的特征.组态分析表明,波函数中权重最大的组态是共价组态1,1,里德伯组态的权重随R的增大而减小,在我们计算的核间距的范围内(0.12 nm＜R＜0.42 nm),权重最大为三分之一.但是,里德伯组态的加入决定了B3Σ态的束缚态特征.里德伯组态的考虑是不可缺少的.

图2(c)是将轨道能量小于2πu的分子轨道4σg和4σu也加入到活性空间中来,从而活性空间包含分子轨道∶2σg,2σu,3σg,3σu,1πu,1πg,4σg,4σu2πu,得到的势能曲线(图2中的曲线(c))势阱更深.

表2给出了图2(b)和图2(c)情况下的Re,De,ωe的值,还列出了Minaev等[23]的CASSCF/augcc-pVTZ计算的结果,以及相应的分子常数的实验值.Minaev等采用的活性空间由分子轨道2σu,3σg,3σu,1πu,1πg,4σg,2πu,2πg构 成. 由表2可见,几种情况的Re值和实验值相比都符合得很好.对比情况(c)和(b),我们发现,由于情况(c)增大了活性空间,波函数中增加了组态,从而大幅度地改善了De值.对于ωe值,三个理论计算的值和实验值都相差20个波数以上.

表2 CASSCF/aug-cc-pVTZ方法计算得到的B3态的分子常数Table 2.The molecular constants for B3state by CASSCF/aug-cc-pVTZ.

表2 CASSCF/aug-cc-pVTZ方法计算得到的B3态的分子常数Table 2.The molecular constants for B3state by CASSCF/aug-cc-pVTZ.

Re/nm De/eV ωe/cm−1情况(b) 0.1610 0.5026 751.0情况(c) 0.1600 1.1649 747.9文献[23] 0.1596 733.6实验值[] 0.1604 1.007 709.1

3.3 B3的icMRCI+Q的计算

3.2 节中图2(c)情况下包含了里德伯组态贡献的CASSCF计算获得B3态的De值相较3.1节中的结果得到改善,ωe的误差还很大,接下来将包含里德伯组态的CASSCF的波函数(3.2节图2(c)情况)为参考组态函数,进行icMRCI+Q计算,采用的基组为aug-cc-pVTZ.大于平衡位置后,采用四个态的态平均计算.得到的B3态的势能曲线如图3粉色点划线所示.

在图3中,为比较方便,我们将所有方法获得的B3势能曲线放入其中,并将它们的平衡位置平移到同一能量值.如预期的那样,由于icMRCI+Q方法中波函数中增加了里德伯组态,计算结果(图3中粉色的点划线)相较于3.2节的图2(c)情况的结果(图3中的绿色的短虚线),更接近基于实验的RKR势能曲线(图3中红色实线)[6].由图3还可以看出,我们的结果要优于Saxon和Liu[7]的结果(图3中黑色的长虚线),原因在于Saxon和Liu采用的基组中没有扩散函数,从而不能正确地描述里德伯轨道,进而缺乏里德伯组态的贡献.

表3 不同来源的B3态的分子常数的比较Table 3.Molecular constants for B3of O2from different work.

表3 不同来源的B3态的分子常数的比较Table 3.Molecular constants for B3of O2from different work.

Re/nm De/eV ωe/cm−1 ωexe/cm−1 Be/cm−1 αe/cm−1 icMRCI+Q 0.16133 0.9914 706.30 9.965 0.8092 0.01513 Saxon[] 0.1627 1.136 724.9 7.04 0.791 0.0077实验值[] 0.1604 1.007 709.1 10.61 0.819 0.0119

图3 (网刊彩色)不同来源的O2的B3Σ 态的势能曲线的比较Fig.3.(color online)The comparison of the potential energy curves for B3state of O2from different sources.

表3进一步给出了基于图3的势能曲线的B3态的分子常数,和图3情形一致,我们的结果与实验值符合得最好.另外,我们的结果和文献[11]的第一个势阱的结果(见表1)相比较,ωe与实验值的偏差从文献[11]的14.5 cm−1下降到2.8 cm−1,特别是De在第一位有效数字得到很大的改善,与实验值的误差从0.1653 eV下降到0.0156 eV.这说明在参考组态中包含里德伯组态对于采用icMRCI+Q方法准确计算B3态是必需的.

4 结 论

本文采用包含Davison修正的内收缩的多参考组态相互作用(icMRCI+Q)的方法,对O2的态进行了计算,参考组态函数是采用完全活性空间组态相互作用方法得到的.首先,采用与文献[11]一样的方法,以共价组态为参考组态,采用aug-ccpV5Z基组,对于和B3态对称性相同的四个态进行态平均计算,发现B3态不存在双势阱结构.文献中双势阱的产生是由于根的振荡现象,即在某一核间距,B3态的势能曲线跳变到23∆ 态的势能曲线上,本文中的态平均计算避免了这种根振荡现象.接着,为了得到理想的计算结果,采用不同活性空间的CASSCF/aug-ccpVTZ方法来计算势能曲线,发现带有2πu轨道电子布居的里德伯组态对B3态的束缚态的特征起决定性作用.最后,通过将2πu轨道加入到活性空间中,从而将相关的里德伯组态加入到参考组态中,对B3态的势能曲线进行了icMRCI+Q/aug-cc-pVTZ计算,得到相较于以往的理论计算与实验值更加相近的势能曲线以及光谱常数.本文探讨里德伯组态的贡献的过程为如何寻找多参考组态相互作用计算中的参考组态、提高理论计算的准确度提供了可以借鉴的途径.

[1]Suzuki D,Kato H,Ohkawa M,Anzai K,Tanaka H,Vieira P,Campbell L,Brunger M J 2011 J.Chem.Phys.134 064311

[2]Krupenie P H 1972 J.Phys.Chem.Ref.Data 1 423

[3]Lewis B R,Gibson S T,Slanger T G,Huestis D L 1999 J.Chem.Phys.110 11129

[4]Chiu S S,Cheung A S,Finch M,Jamieson M J,Yoshino K,Dalgarno A,Parkinson W H 1992 J.Chem.Phys.97 1787

[5]Lewis B R,Gibson S T,Dooley P M 1994 J.Chem.Phys.100 7012

[6]Lewis B R,Berzins L,Carver J H 1986 J.Quant.Spectrosc.Radiat.Transfer 36 209

[7]Saxon R P,Liu B 1977 J.Chem.Phys.67 5432

[8]Buenker R J,Peyerimhof fS D,Peric M 1976 Chem.Phys.Lett.42 383

[9]Tatewaki H,Tanaka K,Sasaki F,Obara S,Ohno K,Yoshimine M 1979 Int.J.Quantum Chem.15 533

[10]Muller T,Dallos M,Lischka H,Dubrovay Z,Szalay P G 2001 Theor.Chem.Acc.105 227

[11]Liu H,Shi D S,Sun J F,Zhu Z L,Zhang S L 2014 Spectrochimica Acta Part A:Molecular and Biomolecular Spectroscopy 124 216

[12]Langhof fS R,Davidson E R 1974 Mol.Int.J.Quantum Chem.8 61

[13]Werner H J,Knowles P J 1984 J.Chem.Phys.82 5053

[14]Knowles P J,Werner H J 1985 Chem.Phys.Lett.115 259

[15]Werner H J,Meyer W 1981 J.Chem.Phys.74 5794

[16]LeRoy R J 2002 University of Waterloo Chemical Physics Research Report CP-655

[17]Woon D E,Dunning T H 1994 J.Chem.Phys.100 2975

[18]Halkier A,Helgaker T,Jørgensen P,Klopper W,Koch H,Olsen J,Wilson A K 1998 Chem.Phys.Lett.286 243

[19]Woon D E,Dunning Jr T H 1995 J.Chem.Phys.103 4572

[20]Jong W D,Harrison R J,Dixon D A 2001 J.Chem.Phys.114 48

[21]Kiljunen T,Eloranta J,Khriachtchev H K,Pettersson M,Räsänen M 2000 J.Chem.Phys.112 7475

[22]Yan B,Pan S P,Wang Z G,Yu J H 2005 Acta Phys.Sin.54 5618(in Chinese)[闫冰,潘守甫,王志刚,于俊华2005物理学报54 5618]

[23]Minaev B F,Minaeva V A 2001 Phys.Chem.Chem.Phys.3 720

(Received 27 January 2017;revised manuscript received 15 March 2017)

Ab initio calculation of the potential curve of B3state of O2∗

Li Chen-Xi1)Guo Ying-Chun1)†Wang Bing-Bing2)
1)(Schoolof Physics and Materials Science,East China Normal University,Shanghai 200241,China)
2)(Laboratory of Optical Physics,Beijing National Laboratory of Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China)

The B3state of O2molecule is an upper state of the most strongly allowed triplet-triplet(B3← X3)absorption,the Schumann-Runge(SR)transition,which plays a crucial role in protecting the earth from suffering UV radiation.Photo-dissociation of O2molecule in the SR transition is the major source of odd oxygen(O and O3)in the stratosphere.Comprehensive knowledge of the electronic states,especially their potential energy curves(PECs),is necessary to understand those phenomena.In this paper,we calculate the PEC of B3state of O2by using the internally contracted multi-reference configuration interaction including Davison correction method,which is denoted by icMRCI+Q,and utilize the complete active space self-consistent field(CASSCF)function as a reference function.The calculation is implemented in the MOLPRO suite of codes.Firstly,we carry out the state-averaged(SA)calculation on the four lowest states,A′3∆u,B3,23∆uand 23Σstates,which are in the same irreducible representation of symmetric group.The active space of CASSCF consists of full valence space.The augmented correlation-consistent aug-cc-pV5Z basis set is used.The results show that the PEC of B3state does not displays double well structure,which is contradictory to Liu’s result(Spectrochimica Acta Part A ∶Molecular and Biomolecular Spectroscopy 2014 124 216).By analyzing the PEC structure,wefind that the double wellof Liu’s result comes from the “rootfl ipping”,that is,the PEC interchange from B3state into 23∆ustate.In our case the “rootfl ipping”is avoided by the SA calculation.Secondly,in order to ensure that the most important configurations are included in the reference function,we calculate the PEC of B3state of O2molecule at CASSCF/aug-cc-pVTZ level by changing the active space.We find that the bound wellof the PEC will not appear unless the active space includes 2πuorbital which is beyond the full valence space.That means that the Rydberg configurations including 2πuorbital play a crucial role in forming the bound well.And the result is further improved by adding into the active space another two orbitals 4σgand 4σuwhose orbital energies are both less than 2πu.Finally,we add the Rydberg configurations into the multi-reference configuration function by putting 2πu,4σg,4σuinto the active space and then carry out the calculation at an icMRCI+Q/aug-cc-pVTZ level.The obtained B3state PEC and its spectroscopic constants are in good agreement with the experimental data compared with previous results.Moreover,the process we determine the reference configurations is useful for making accurate calculation at an MRCI levelon other species.

∶B3state of O2,internally contracted multi-reference configuration interaction,potential energy curve,spectroscopic constants

PACS∶31.15.A—,31.15.xr,31.50.DfDOI∶10.7498/aps.66.103101

∗国家自然科学基金(批准号:11474348,61275128)资助的课题.

†通信作者.E-mail:ycguo@phy.ecnu.edu.cn

©2017中国物理学会Chinese Physical Society

PACS∶31.15.A—,31.15.xr,31.50.DfDOI∶10.7498/aps.66.103101

*Project supported by the National Natural Science Foundation of China(Grant Nos.11474348,61275128).

†Corresponding author.E-mail:ycguo@phy.ecnu.edu.cn